Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Light-induced degradation of methylammonium tin iodide absorber layers†
Joana Ferreira
Machado
 ,
Jeremy
Hieulle
,
Jeremy
Hieulle
 ,
Aline
Vanderhaegen
,
Aline
Vanderhaegen
 and
Alex
Redinger
and
Alex
Redinger
 *
*
Department of Physics and Materials Science, University of Luxembourg, Luxembourg City L-1511, Luxembourg. E-mail: alex.redinger@uni.lu
First published on 22nd November 2024
Abstract
Light-induced degradation of tin-based organic inorganic halide perovskite (Sn-HOIP) absorbers is a major barrier for their deployment in photovoltaic applications. Sn-HOIPs are believed to intrinsically degrade due to the tendency of tin to change the oxidation state from (+2) to (+4). So far, most studies have been performed on absorbers that were synthesized with solvent-based techniques. The solvents themselves have been associated with Sn-HOIP degradation. Here, we show that in solvent-free coevaporated methylammonium tin iodide (MASnI3) films exposed to white light, no Sn(+4) could be detected, even after almost 100 h of exposure. To understand the degradation mechanism, the chemical composition at the surface of MASnI3 was measured by X-ray photoelectron spectroscopy after different illumination intervals. The measurements showed that MASnI3 decomposed into tin iodide (SnI2) and a minimal amount of metallic tin. The SnI2 phase at the surface increases as a function of light exposure. Despite the strong degradation, light-induced decomposition was not accompanied by the formation of Sn(+4). In addition, the stability of SnI2 under illumination was studied and compared to that of PbI2. Here, SnI2 did not show any degradation, in contrast to PbI2, which degraded into metallic lead. Our results show that the tendency of tin to be in multiple oxidation states is not triggered by light. Instead, the critical point is the choice of an organic component (methylammonium) that leaves the perovskite crystal during illumination. These results show that it is essential to retain the organic component in the perovskite lattice, either by including additives or by replacing the organic component.
1 Introduction
Halide organic–inorganic perovskites are attracting attention in the photovoltaic community due to their fast evolution in power conversion efficiency (PCE). In little more than 10 years, the PCE of halide perovskites increased from 3.8% to 26.1% on the laboratory scale.1–4 This record efficiency is comparable to the record for silicon solar cells, which is a well-established material for photovoltaic applications.4,5Despite its extraordinary properties, the toxicity of lead remains one of the major challenges, as the residues of degraded lead perovskite can dissolve in water and this is a concern for public health and the environment.6–8 So far, Sn-based perovskite solar cells have been considered the most promising replacement for Pb-based ones, with their PCE record already exceeding 14%.9,10 This efficiency was obtained by doping a formamidinium tin iodide (FASnI3) based absorber with tin fluoride (SnF2), which has been reported to improve the stability and efficiency of Sn-based perovskites.11–13
Nevertheless, Sn-based solar cells are still less stable than their lead counterparts and their degradation has been attributed in numerous studies to the tendency of Sn to oxidize from Sn(+2) to Sn(+4) when exposed to moisture, oxygen, heat and light.14,15 The degradation and low efficiencies are even more obvious in methylammonium tin iodide (MASnI3) based solar cells, where the current record PCE is 7.13%.16
In terms of optoelectronic properties, MASnI3 films exhibit high photoluminescence quantum yields and the peak has been reported to be around 1.3 eV, which corresponds to the optimum bandgap for single junction solar cells.16–18 The same articles report very short carrier lifetimes, which were attributed to fast recombination due to defects and self-doping.
Multiple stability studies have been performed on Sn-based perovskites, where Sn-perovskites (ASnX3) are found to easily oxidize and form double perovskites (A2SnX6)19,20 or decompose into AI, SnO2 and SnI4 and eventually form I2.21 Note that A can be an organic cation, such as methylammonium or formamidinium, or an inorganic one, such as cesium. SnI4 has been considered the main contributor to the degradation of Sn-perovskites and was even found to cause cyclic degradation of perovskite films.15 Furthermore, Sn oxidation from the oxidation state of Sn(+2) to Sn(+4) has already been shown to cause self-p-doping in the absorber, resulting in loss of PCE.15,22 This effect was found to be more predominant in MASnI3 than in FASnI3.14
It is worth mentioning that a large majority of the perovskite studies so far have been performed on absorbers that were synthesized via chemical, solvent-based methods. Although this growth method produces films for high-performance devices,3,9 the use of dimethylsulfoxide (DMSO) as a solvent has also been associated with the oxidation of Sn in the precursor solution.23–25 X-ray photoelectron measurements show that solvent-grown Sn-perovskite absorbers contain Sn(+4) even when they are fresh,15,16,25–28 while thermally evaporated films with physical vapor deposition (PVD) can be grown without Sn(+4).26,29
From all the stresses that perovskites are sensitive to, light degradation seems to be of the highest importance, since every solar cell needs light to produce electricity. Therefore, it is not acceptable that light promotes the decomposition of solar cells and there is an urgent need to understand the exact mechanisms of degradation. Thorough studies of light degradation in perovskites have already been done. For lead perovskites, it was found that the degradation mechanism under light illumination is such that the Pb perovskite first degrades to PbI2 and then PbI2 degrades to Pb(0).30–35
Although there seems to be a consensus that MA+ tends to leave the surface of methylammonium-containing perovskites upon illumination,36–38 there is no clear agreement on the residues remaining on the surface of the sample.28,38,39 Furthermore, all reports containing chemical analysis of Pb-free perovskites include only solvent-grown absorbers, adding another variable to their degradation study. A light degradation study of solvent-free Sn-perovskites is crucial for understanding light-induced degradation, without the deterioration effects of the solvents in the absorber.
In this study, we performed a detailed chemical analysis of light-degraded MASnI3 absorbers that were grown using physical vapor deposition (PVD). This growth technique has previously been shown to form nominally Sn(+4)-free absorbers.26 Additionally, the samples in this study were always kept in an inert gas or ultra-high vacuum (UHV) to minimize degradation due to contaminants such as oxygen or moisture. This is important since all external stresses are likely to contribute to degradation.
Compositional measurements were performed using X-ray photoelectron spectroscopy (XPS) after the sample was illuminated for different intervals of time. This technique is highly sensitive to changes in the composition and allowed us to distinguish between the different oxidation states of Sn, i.e. Sn(0), Sn(+2) and Sn(+4). The chemical analysis is complemented by surface measurement of topography and the work function of the fresh sample, using atomic force microscopy (AFM) and Kelvin probe microscopy (KPFM), which have been previously used to identify the presence of secondary phases, such as PbI2, in Pb-perovskites.31 Furthermore, photoluminescence (PL) and time-resolved photoluminescence (TRPL) measurements were performed to assess the quality of the fresh sample.
We show that MASnI3 formed SnI2 on the surface and lost MAI upon illumination. The degradation was not accompanied by the formation of Sn(+4), which highlights that the change in the oxidation state from +2 to +4 was not triggered by light. The KPFM measurements revealed no secondary phase on the MASnI3 surface, unlike the observations typically made with Pb-containing perovskites. In contrast, our XPS results indicate that a uniform SnI2 layer forms on the surface of the perovskite and thickens over time under illumination. From the temporal evolution of the elemental ratios, deduced by XPS, a model was developed that allowed us to estimate the thickness of the SnI2 layer as a function of light exposure time.
Given the degradation mechanism and the tendency of Sn(+2) to decompose into Sn(+4),15,22 complementary measurements of XPS were done on light exposed SnI2 films. The impressive stability of SnI2 under illumination indicated that the organic cation is the main cause of the degradation induced by the light of Sn perovskites. Interestingly, SnI2 is much more stable against light exposure than PbI2.
2 Methods
2.1 Synthesis
MASnI3 samples were grown on ITO substrates using physical vapor deposition (PVD). Before deposition, ITO substrates, provided by Lumtec, were cut into approximately 7 mm squares, which were cleaned in a sequence of six ultrasonic baths at 50 °C. Each bath lasted 4 minutes and each contained a different liquid, namely an aqueous solution of Helmanex 2 wt%, DI water twice, ethanol, acetone, isopropanol and finally DI water. Then each substrate was blow dried with N2 and ozone treated for 15 minutes. After the cleaning procedure, the substrates were immediately stored in a glovebox. The SnI2 and the methylammonium iodide (MAI) powders were provided by Tokyo Chemical Industry (TCI), product number M2556. During thermal evaporation, the pressure was kept at 1 × 10−5 mbar with the source temperature of SnI2 at T = 265 °C and the CH3NH3I powder was kept at a temperature between T = 98 °C and T = 108 °C such that the pressure in the chamber would be constant during deposition. The deposition time was set to 90 minutes to obtain films of approximately 300 nm thickness. The PVD was performed in a vacuum chamber embedded in a glovebox; therefore, the samples were never exposed to air or moisture and were always under a N2 atmosphere or vacuum. The samples were transferred to the ultra-high vacuum (UHV) via dedicated suitcases.The SnI2 and the PbI2 films were also deposited on ITO. The SnI2 was evaporated at 265 °C, whereas the PbI2 was evaporated at 300 °C. For every deposition, the substrate was at nominal room temperature T = 21 °C (±2 °C).
2.2 Characterization
XPS measurements were performed with a Prevac EA15 analyzer under UHV at a pressure of 5–9 × 10−10 mbar during the measurements. The X-ray source was a non-monochromatic Mg Kα source. During measurement, the acceleration voltage was 12 kV and the emission current was 25 mA. The pass energy was set to 50 eV and a rectangular lens slit of 2.5 cm × 25 mm was employed. The raw data from the MASnI3 and SnI2 samples were corrected for each element using Scofield factors and a calibration transmission function, which was determined by high resolution measurement of reference samples.40In order to further reduce the systematic errors of the XPS system, PbI2 and SnI2 samples were used as standards to have the correct ratios for I/Sn and I/Pb. For each binding energy region, multiple individual high-resolution scans were performed to verify whether the sample exhibited charging. Since in this case there was no charging, the average of the scans was used.
The non-monochromatic X-ray source produces multiple emission lines, which produce satellite peaks in the measurement. In the case of Mg Kα, satellite peaks are expected with a shift of −8.4 eV and −10.2 eV in binding energy and a respective relative intensity of 8% and 4% compared to the main peak.41 In the case of Sn3d and I3d orbitals, the satellite peak of the 3/2 peak overlaps with the main 5/2 peaks, and therefore satellite peaks have to be considered in the fitting.
The background signal was subtracted with W Tougaard and U2 Tougaard for Sn3d and I3d, respectively, and the Shirley background was used for C1s and N1s. The Sn3d and I3d peak fitting was performed with the Lorentzian asymmetric lineshapes LA and TLA, respectively, while the C1s and N1s were fitted with a Gaussian/Lorentzian sum (SGL) lineshape. Satellite peaks were fitted with Gaussian fitting.
Various fitting constraints were used for the XPS measurements. The energy separation between the spin–orbit split peaks 3/2 and 5/2 (ΔEB) was fixed to 11.5 eV for the I3d peaks and 8.41 eV for Sn3d, according to the literature, for both the main peaks and the satellite peaks. Additionally, the 3/2 peak intensity was set to 2/3 of the 5/2 peak intensity and the full width at half maximum (FWHM) was the same for every peak of the same element. The FWHM of the Sn peaks and the binding energy of Sn(0) were determined by measuring and fitting a sputtered pure metallic tin plate. The binding energies of Sn(+2) and Sn(+4) were determined by measuring the same tin plate after oxidation (before sputtering under UHV) as described in ref. 26. Peak fitting was performed using CasaXPS software.
The sample was exposed to light in the XPS chamber, using a quartz tungsten-halogen lamp (Thorlabs QTH10) shining through a borosilicate vacuum viewport. The window was equipped with a lead-glass radiation protection (Allectra) to block X-ray radiation. Transmission measurements carried out on windows with and without the lead glass showed very little difference in the visible and near infrared light spectra. In order to avoid errors, the sample was never moved from its initial position for the whole set of measurements, with an irradiance of 16 mW·cm−2 (0.16 sun) at the sample position.
In order to assess the optoelectronic quality of the absorber layers, photoluminescence (PL) measurements are spectrally corrected and intensity calibrated to reproduce the illumination under 1 sun equivalent conditions according to the AM1.5 solar spectrum. The setup and calibration procedure are explained in ref. 42. Measurements were performed with an InGaAs detector (Andor iDus DU490A-1.7) ranging from 900 to 1600 nm. To excite the sample, a diode laser of wavelength 660 nm was used, with an output power of 2.61 × 10−1 W cm−2, resulting in a corresponding photon flux of 2.17 × 1017 cm2 s−1.
Time-resolved photoluminescence (TRPL) measurement was performed using a pulsed laser with a wavelength of 639 nm. The duration of the laser pulse was approximately 70 ps and the excitation power density was estimated to be 4.584 × 10−2 W cm−2 at a repetition frequency of 20 MHz. During PL and TRPL measurements, the sample was placed in a box with a quartz window and constant N2 flow.
Atomic force microscopy (AFM) and Kelvin probe force microscopy (KPFM) measurements were performed using an Omicron variable temperature scanning probe microscope (VT-SPM) in UHV operating in the low 10−10 mbar range. Topography measurements were performed in frequency modulation mode, with an excitation amplitude of 0.5 V at a frequency shift of −3 Hz. KPFM measurements were performed simultaneously with the topography measurements via side-band excitation in frequency modulation mode (FM mode), significantly increasing the measurement resolution by reducing the contribution from the large tip cone and from the cantilever. An AC voltage of 0.4 V was used at an oscillation frequency of 965 Hz. Additionally, for higher resolution, the tip used was the APEX high resolution tip, i.e. a doped diamond tip manufactured by Adama Innovations, with a quality factor (q-factor) in a vacuum of 9500 (±400).
3 Results and discussion
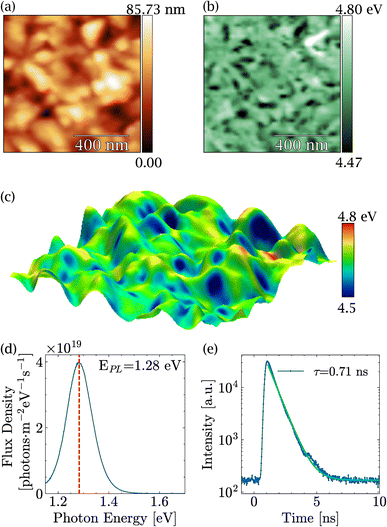
Before discussing the impact of light on MASnI3, in-depth characterization of the PVD-grown films was carried out and is summarized in Fig. 1. Fig. 1(a) shows a typical topography of a MASnI3 film measured by AFM under ultra-high vacuum directly after growth, where the typical polycrystalline structure of perovskites was visible.43,44 Grains several hundred nanometers in size could be identified, separated by grain boundaries. In order to identify possible secondary phases, KPFM measurements were performed at the same spot. For the case of Pb-based halide perovskites, KPFM has proven to be extremely viable to identify secondary phases such as PbI2, which exhibited distinct work functions compared to perovskites.31 In fact, variations in the work function of approximately 300 meV were found as shown in Fig. 1(b) and in the work function distribution Fig. S1.† An average work function of 4.63 eV with a standard deviation of 0.05 eV was measured, which was in close agreement with the literature.45Since the material was polycrystalline, differences in work function may arise as a result of not only different materials but also different crystallographic facets with distinct surface dipoles. A three-dimensional overlay of the topography and the work function shown in Fig. 1(c) suggests that most of the variations were due to different facets, since the low work function regions were restricted to parts of the grains only. From these measurements, we concluded that there were no obvious secondary phases at the surface of the films, which meant either that the film was phase pure or that the secondary phase exhibited exactly the same work function as the perovskite.
The PL peak of MASnI3 appeared at a value of 1.28 eV with a strong PL intensity (see Fig. 1(d)). From the calibrated measurements, a photoluminescence quantum yield Qlume = 2 × 10−3. Qlume was found to be in agreement with other samples synthesized via coevaporation.26 The non-radiative losses, as estimated from kBT × ln(Qlume) amount to −155 meV, which is, a priori, a very favorable value for high-efficiency solar cells. The drawback of MASnI3 is shown in Fig. 1(e), where TRPL measurements carried out on the pristine sample showed a decay time of only 0.71 ns, which is extremely fast compared to hundreds of nanoseconds of their lead counterparts.46 Such PL intensity values and low lifetimes in MASnI3 have been reported in multiple studies and have been attributed to fast carrier recombination and excessively doped absorbers,16–18 which is in line with the results presented here.
The high Qlume value combined with the fast decay time showed that these samples were highly doped. Using the formalism introduced in ref. 46, the doping level could be approximated to be 2 × 1018 cm−3. The high doping levels in MASnI3 have been justified by the presence of Sn(+4) in previous reports.47
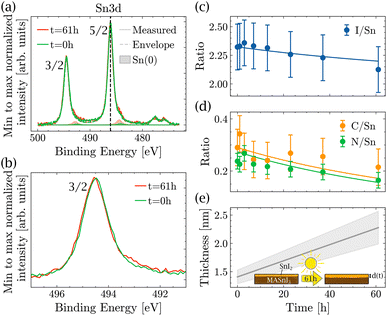
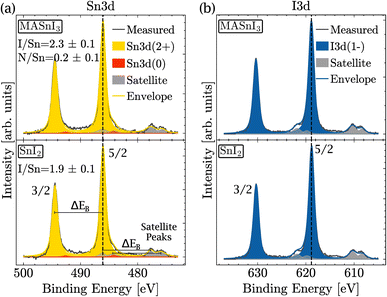
Therefore, XPS was performed to measure the amount of Sn(+4) in the near surface region of the film. In order to identify the different oxidation states as precisely as possible, the coevaporated MASnI3 films were always compared to reference SnI2 films. Therefore, the position, FWHM and composition could be deduced with high accuracy. Fig. 2(a) shows a high resolution scan of the Sn3d region of a MASnI3 film (top) and a SnI2 film (bottom), where the Sn(+2) component is highlighted in yellow and the Sn(0) component is shown in red (see the Methods for the fitting procedure). Satellite peaks, due to the use of a non-monochromatic X-ray source, are shown in gray and had to be taken into account in the fitting of Sn3d, as they overlapped with the orbital Sn(+2). Fig. S2† highlights the difference in the Sn(0) fitting when the satellites are taken into account compared to when they are ignored.
 | ||
| Fig. 2 Detailed XPS spectra of MASnI3 (top) and SnI2 (bottom) at (a) the Sn3d core-level and (b) the I3d core-level. | ||
The energy difference between the 3/2 orbital and the 5/2 orbital is denoted by ΔEB. Note that within a single element, ΔEB remained constant for the main peaks and for the satellite peaks. The positions of the satellite peaks for non-monochromatic sources are tabulated in ref. 41.
From the measurements shown in Fig. 2(a), it was found that the MASnI3 films essentially contained Sn in the oxidation state (+2), as expected for pure MASnI3 and in pristine SnI2. There was probably a very small contribution of metallic Sn (oxidation state 0), although the quantity was very small and within the fit error, that is, 98% of Sn(+2) and 2% of Sn(0).
Note that Sn(0) was included in this fitting for consistency only. As shown later in the manuscript, the amount of Sn(0) increased as a result of light illumination. As a consequence, the Sn(0) component was already included in this spectrum. It should be stressed that, for the pristine sample shown here, the fitting result was equally fine without considering Sn(0). Importantly, the amount of Sn(+4) in the samples was lower than the detection limit. This was unexpected since the PL analysis and the high doping levels actually suggested that there was a considerable amount of Sn(+4).
The detailed scan in the I3d energy region is shown in Fig. 2(b). Similarly to the Sn region, the measurement was performed on MASnI3 (top) and on SnI2 (bottom). For both samples, the oxidation state I(−1) is shown in blue and the satellite peaks are shown in gray. Both samples only contained the oxidation state I(−1), which was the oxidation state expected for pure MASnI3 and SnI2 films.
Fig. 2(a) shows that the binding energies of Sn(+2) in MASnI3 and SnI2 were very similar (with only a 0.01 eV difference) and therefore it was not possible to identify an SnI2 secondary phase in the MASnI3 films by considering the binding energy only. The same conclusion held for the I3d binding energy in Fig. 2(b) (with a difference of 0.04 eV).
As discussed in the Methods section, the SnI2 sample was used to calibrate the I/Sn ratio. For this particular sample, a value of 1.9 (±0.1) was deduced, which was expected. The I/Sn ratio deduced from the MASnI3 sample equaled only 2.3 (±0.1) instead of the expected value of 3. Similarly, the measured N/Sn ratio was lower than the expected value, with 0.2 (±0.1) instead of 1. The only plausible secondary phase, which exhibited a ratio I/Sn that was lower than three combined with an oxidation state Sn(+2), was SnI2.
Therefore, we speculated that the discrepancy in the ratio for MASnI3 was probably caused by a thin layer of SnI2 on top of the perovskite. The presence of MASnI3 and SnI2 was also confirmed by X-ray diffraction (Fig. S3†), where reflection peaks are visible for both materials. Furthermore, since XPS provides the chemical composition of the topmost 10 nm, the low I/Sn and low N/Sn ratios do not contradict the bulk-sensitive PL and XRD measurements, which showed that the 300 nm thick sample is indeed MASI perovskite. XPS provides further information on the chemical composition of the top surface of the sample. To identify the source of this deviation, light-induced degradation of MASnI3 was investigated. In order to gain a full picture of the compositional changes occurring at the surface, tin, iodine, carbon, nitrogen, and oxygen signals were monitored as a function of white light exposure time.
The light-induced degradation measurements were made in the following way: a pristine MASnI3 sample was exposed to light in a vacuum for different time intervals. After each interval, it was measured using XPS. All variations in composition that could be due to XPS or vacuum degradation were taken into account in the measurement error bar. The total exposure time to light summed up to 61 hours. Fig. 3(a) shows the spectra in the Sn3d energy region performed on a pristine sample and after 61 h of light exposure. For better visibility, the Sn(+2) peaks and the satellite peaks were omitted, but were taken into account in the fit. A small increase in Sn(0) was observed, but no formation of Sn(+4) was detected. Fig. 3(b) shows the background subtracted raw data in the Sn3d 3/2 peak region. A small shoulder formed on the lower binding energy side, which was due to the higher content of Sn(0). Note that in the Sn3d 3/2 peak, there was no contribution from the satellite peaks, which makes the identification of Sn(0) much easier. We would like to stress that the changes observed for Sn(0) were small and usually such variations are difficult to interpret. In the present case, the position of the sample did not change at all and all measurements were done consecutively, which was the only way to measure such small differences.
Note that the topography of the sample does not change significantly after light exposure (see Fig. S4†), making it impossible to identify the degradation through topography. Furthermore, as mentioned previously, it was not possible to track the degradation by looking at the binding energy of the peaks alone. The peak position of Sn(3d) did not change during light exposure. However, when looking at the ratios of I/Sn, C/Sn and N/Sn (Fig. 3(c) and (d)), all three ratios decreased as a function of light exposure, suggesting that the amount of MAI decreased as a function of time.
In the literature, MAPbI3 is known to degrade into MAI (or fragments of MAI) and PbI2.31,33,34 Assuming that MASnI3 has a degradation pathway similar to that of MAPbI3, then MAI losses increase the amount of SnI2 in the films and the reaction is as described by eqn (1).
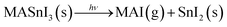 | (1) |
That is, if MAI is assumed to leave the MASnI3 surface in gas form, then the ratio I/Sn goes from 3 to 2 and the ratio N/Sn goes from 1 to 0. Here, MAI is considered as the entire MAI molecule, but it could also be smaller fragments of MAI.
To test whether the degradation pathway proposed in eqn (1) is valid and compatible with the measured XPS ratios, a two-layer model was used, which is described below. Since the I/Sn ratio was lower than 3 already at the beginning of the measurement, it is plausible to assume that a thin layer of SnI2 was already present from the beginning. If MASnI3 decomposes according to eqn (1), then the thickness of SnI2 should increase over time. Consequently, changes in elemental ratios should allow one to deduce the increase in the thickness of the SnI2 layer as a function of time.
This two-layer model is well established in the XPS community and, for instance, described in the book by Hofmann and Siegfried.41 The measured intensity of an element x in a two-layer system has two contributions: one related to the surface material and the other related to the bulk material. The surface contribution increases exponentially with the thickness d of the top layer, whereas the bulk contribution decreases exponentially with d. The intensity of an element x can therefore be expressed as
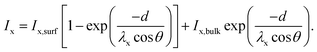 | (2) |
I x is the measured intensity divided by the sensitivity factors determined by Scofield,40 and Ix,surf and Ix,bulk are the intensities of the element x in the pure surface material and in the pure bulk material, respectively. θ is the angle between the normal of the sample surface and the analyzer lenses, in the framework of this study θ = 0°, and λx is the inelastic mean free path (IMFP) of the element x in the surface material. It is worth mentioning that in the formula established by Hofmann and Siegfried, λx stands for the effective attenuation length (EAL) of the electrons of the element x in the surface materials. The EAL depends on both the elastic and inelastic scattering, but here, for simplicity, the elastic scattering contribution is neglected and the inelastic mean free path (IMFP) is used instead. According to Hofmann and Siegfried, this approximation introduces an error of 10–15% in the value of λ.
Here, the value of interest was the ratio between x and Sn (x/Sn or Rx,Sn for better readability), which can be obtained by dividing the intensity Ix by ISn. The complete derivation of this ratio can be found in the ESI (Section 4),† and the final equation for this ratio is given by
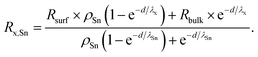 | (3) |
R surf and Rbulk are the expected ratios x/Sn in the surface layer and in the bulk, respectively, and ρSn is the ratio of the volume density of Sn in the bulk and on the surface.
Assuming that the SnI2 formation occurs layer by layer, then the thickness d was a function of the light exposure time t. Furthermore, the initial thickness of the MASnI3 layer (approximately 300 nm) was two orders of magnitude larger than the SnI2 thickness; therefore, it was considered as an infinite reservoir. As a consequence, degradation evolved linearly in time and therefore d(t) = d(0) + b × t, where d(0) is the initial thickness of the SnI2 layer and b is the MASnI3 decomposition rate under light exposure.48
The datasets of N/Sn, C/Sn and I/Sn were fitted with d(0), b and ρSn as free parameters, such that they are the same for all three data sets. The IMFPs were calculated using the model derived by Tanuma et al. (TPP2M).49 From the fitting, an initial SnI2 thickness d(0) of 1.4 ± 0.1 nm was obtained and the thickness d(t) increased at a rate of b = 0.014 ± 0.003 nm h−1. The ratio of Sn in the overlayer to the bulk was ρSn = 2.71 ± 0.33, which was in good agreement with the tabulated values ρcalcSn = 4.2 (see Section 5 of the ESI†). According to the model, after 61 h of exposure to light, the SnI2 reaches a thickness of d(61 h) = 2.3 ± 0.3 nm, representing an almost two-fold increase.
The KPFM-measured work functions also confirmed this model. In fact, the work function of MASnI3 decreases from 4.63 eV in the pristine sample to 4.61 eV after illumination, which is a negligible variation. This work function was very similar to the work function of SnI2 (4.7 eV), which was confirmed on an SnI2 only sample.
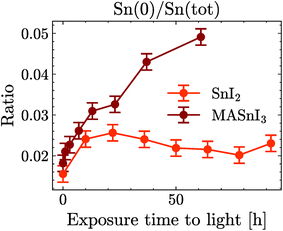
The degradation of MASnI3 in SnI2 was similar to what was observed in previous reports for Pb-based perovskites,30–35 which degrade into PbI2. However, the same reports mention that PbI2 additionally decomposed into Pb(0). Surprisingly enough, in the data shown here only a minimal amount of Sn(0) was observed and the Sn(+4) remained lower than the detection limit for the duration of the experiment. To assess the stability of SnI2 against light, a degradation study was performed on films of pure SnI2 and pure PbI2. This allowed for a comparison of their degradation upon exposure to light.
Fig. 4(a) shows the ratio I/Sn of SnI2 and the ratio I/Pb of PbI2 as a function of illumination time. Although both ratios were similar at time t = 0 h, the I/Sn ratio in SnI2 remained stable for almost 100 h of light exposure, while the I/Pb ratio in PbI2 started to decrease after 4 h of exposure and continued to decrease over time. Similarly, in Fig. 4(b), the Sn(0) content in SnI2 was negligible and remained stable under long-duration illumination, while the Pb(0) content increased significantly over time. No Sn(+4) formation was observed upon illumination of SnI2. This set of measurements showed that SnI2 was much more stable than PbI2 under illumination in UHV and the secondary phases of SnI2 in MASnI3 will not degrade further into Sn(0), unlike Pb-based perovskites.
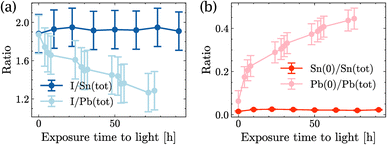 | ||
| Fig. 4 Time evolution of SnI2 and PbI2 under light illumination: (a) quantity of iodide and (b) quantity of Sn(0) in SnI2 and quantity of Pb(0) in PbI2. | ||
Finally, Fig. 5 shows the evolution of Sn(0) in MASnI3 and SnI2 under illumination. Notice that while the quantity of Sn(0) increased when MASnI3 was illuminated, the quantity of Sn(0) in SnI2 remained stable. This is an important result, as the formation of metallic Sn in MASnI3 was not triggered by the decomposition of SnI2 but by the perovskite itself. Recalling eqn (1), the light-induced degradation pathway must be written as
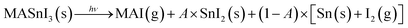 | (4) |
The factor A is a value between zero and unity and describes the probability that MASI decomposes into SnI2versus a direct decomposition into metallic Sn. In Pb-based perovskites, the direct decomposition of MAPbI3 into metallic Pb was very difficult to measure via XPS since it was shown that PbI2 decomposed into metallic Pb at a faster rate than Pb-based perovskites.31 However, for Sn-based perovskites, this could now be measured directly, as SnI2 does not seem to be photosensitive.
The constant value of Sn(0) in SnI2 should also be discussed. The value was extremely small, but still outside the statistical error of the fit. However, this did not mean that the Sn(0) value was in fact greater than zero in the SnI2 films. The background in XPS and the lineshape also impacted the fit result. Our current understanding is that the Sn(0) in SnI2 is likely to be the resolution limit. Importantly, the increase of the Sn(0) in MASnI3 is not impacted by this since pristine samples showed very similar values for Sn(0) to those in SnI2, which then increased, while keeping the fit routine constant.
Most importantly, the light instability of MASnI3 under vacuum is not due to a change in the oxidation state from Sn(+2) to Sn(+4). Therefore, light-induced degradation is not triggered by the instability of the oxidation state of Sn. In fact, here Sn is shown to be even more tolerant than Pb. Instead, the light-induced decomposition of MASnI3 appears to arise from the choice of the organic component. As calculations in the literature have shown, MA+ in the perovskite lattice has strong dynamics.50–52 The organic cation moves and rotates with the cage, causing lattice distortion and lattice softness. This motion is probably reinforced by light exposure, where additional energy is given to the system, which contributes to the instability of MASnI3. This also means that the best way to stabilize Sn-based perovskites is to move away from MAI, which is the source of intrinsic instability in the perovskite. Importantly, the SnI2 secondary phase is not photosensitive, which offers a great advantage compared to the Pb-based system. In the state-of-the-art Pb-based perovskite, residual PbI2 will lead to long-term stability problems, which can be prevented by the use of Sn.
3.1 Summary
In this study, we used XPS, KPFM and photoluminescence based techniques to understand light-induced degradation of MASnI3. In contrast to most reports in the literature, we show that, in UHV, decomposition of the near surface region does not induce Sn(+4). Most of the MASnI3 transforms into SnI2 when exposed to light and a negligible amount into Sn(0). In contrast to Pb-based halide perovskites, SnI2 does not decompose into Sn(0) and I2 but remains stable against prolonged light exposure. This is certainly a big advantage for Sn-based perovskites compared to Pb-based ones. Despite the improved stability of SnI2 compared to PbI2, high doping levels are also problematic for coevaporated Sn-based perovskites. Despite the fact that we did not detect any Sn(+4), the combination of PLQY and TRPL allowed us to deduce doping levels in the order of 1018 cm−3. In order to make Sn-based perovskites a true alternative to Pb-containing ones, the use of MAI needs to be prevented and the doping level needs to be reduced to an acceptable level. Our research suggests that the high doping levels in Sn-based perovskites are not due to the presence of Sn(+4), as previously thought in the literature. To advance the development of lead-free perovskite solar cells, it is crucial to identify the real source of this high doping in Sn-based perovskites. This knowledge will enable the formulation of effective strategies to control doping levels in these materials.Furthermore, we have found that the photochemical conversion of MASnI3 into SnI2 is a major factor limiting the long-term intrinsic stability of Sn-based perovskites. A more detailed investigation into the photochemical stability of Sn-based perovskites is necessary to propose mitigation strategies, such as the use of different organic cations or encapsulation methods.
Data availability
The data supporting this article have been included as part of the article and the ESI.† Raw data files can be sent to the reader upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge funding from the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) within SPP 2196 (project number 423876021) and the Luxembourg National Research Fund (FNR) (grant references: 11244141, 13390539, and 14757355). The authors acknowledge Anastasios-Sevastianos Antoniou for measuring the SnI2 work function. Susanne Siebentritt and Ricardo Poeira for useful discussions. The authors acknowledge technical support of B. Uder, U. Siegel, and R. Himelrick.References
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050–6051 CrossRef CAS.
- University of Science and Technology of China (USTC), USTC Set New Record in Perovskite Cell Efficiency, 2023, https://en.ustc.edu.cn/info/1007/4676.htm, accessed: 2024-06-01 Search PubMed.
- Z. Liang, Y. Zhang, H. Xu, W. Chen, B. Liu, J. Zhang, H. Zhang, Z. Wang, D. H. Kang, J. Zeng, X. Gao, Q. Wang, H. Hu, H. Zhou, X. Cai, X. Tian, P. Reiss, B. Xu, T. Kirchartz, Z. Xiao, S. Dai, N. G. Park, J. Ye and X. Pan, Nature, 2023, 624, 557–563 CrossRef CAS PubMed.
- National Renewable Energy Laboratory (NREL), Best Research-Cell Efficiency Chart, 2024, https://www.nrel.gov/pv/cell-efficiency.html, accessed: 2024-05-28 Search PubMed.
- LONGi, LONGi Sets a New World Record of 27.09% for the Efficiency of Silicon Heterojunction Back-Contact (HBC) Solar Cells, 2023, https://www.longi.com/en/news/heterojunction-back-contact-battery/, accessed: 2024-06-01 Search PubMed.
- J. Li, H. L. Cao, W. B. Jiao, Q. Wang, M. Wei, I. Cantone, J. Lü and A. Abate, Nat. Commun., 2020, 11, 1–5 CrossRef CAS.
- A. Babayigit, D. Duy Thanh, A. Ethirajan, J. Manca, M. Muller, H. G. Boyen and B. Conings, Sci. Rep., 2016, 6, 1–11 CrossRef.
- A. Babayigit, A. Ethirajan, M. Muller and B. Conings, Nat. Mater., 2016, 15, 247–251 CrossRef CAS PubMed.
- B. B. Yu, Z. Chen, Y. Zhu, Y. Wang, B. Han, G. Chen, X. Zhang, Z. Du and Z. He, Adv. Mater., 2021, 33, 1–10 Search PubMed.
- G. Liu, X. Jiang, W. Feng, G. Yang, X. Chen, Z. Ning and W. Q. Wu, Angew. Chem., Int. Ed., 2023, 62, 1–10 Search PubMed.
- M. H. Kumar, S. Dharani, W. L. Leong, P. P. Boix, R. R. Prabhakar, T. Baikie, C. Shi, H. Ding, R. Ramesh, M. Asta, M. Graetzel, S. G. Mhaisalkar and N. Mathews, Adv. Mater., 2014, 26, 7122–7127 CrossRef CAS.
- T. M. Koh, T. Krishnamoorthy, N. Yantara, C. Shi, W. L. Leong, P. P. Boix, A. C. Grimsdale, S. G. Mhaisalkar and N. Mathews, J. Mater. Chem. A, 2015, 3, 14996–15000 RSC.
- A. G. Kontos, A. Kaltzoglou, E. Siranidi, D. Palles, G. K. Angeli, M. K. Arfanis, V. Psycharis, Y. S. Raptis, E. I. Kamitsos, P. N. Trikalitis, C. C. Stoumpos, M. G. Kanatzidis and P. Falaras, Inorg. Chem., 2017, 56, 84–91 CrossRef CAS.
- F. Wang, J. Ma, F. Xie, L. Li, J. Chen, J. Fan and N. Zhao, Adv. Funct. Mater., 2016, 26, 3417–3423 CrossRef CAS.
- L. Lanzetta, T. Webb, N. Zibouche, X. Liang, D. Ding, G. Min, R. J. E. Westbrook, B. Gaggio, T. J. Macdonald, M. S. Islam and S. A. Haque, Nat. Commun., 2021, 12, 2853 CrossRef CAS.
- F. Li, C. Zhang, J. H. Huang, H. Fan, H. Wang, P. Wang, C. Zhan, C. M. Liu, X. Li, L. M. Yang, Y. Song and K. J. Jiang, Angew. Chem., Int. Ed., 2019, 58, 6688–6692 CrossRef CAS PubMed.
- N. K. Noel, S. D. Stranks, A. Abate, C. Wehrenfennig, S. Guarnera, A. A. Haghighirad, A. Sadhanala, G. E. Eperon, S. K. Pathak, M. B. Johnston, A. Petrozza, L. M. Herz and H. J. Snaith, Energy Environ. Sci., 2014, 7, 3061–3068 RSC.
- W. Ke, C. C. Stoumpos, I. Spanopoulos, L. Mao, M. Chen, M. R. Wasielewski and M. G. Kanatzidis, J. Am. Chem. Soc., 2017, 139, 14800–14806 CrossRef CAS PubMed.
- D. J. Kubicki, D. Prochowicz, E. Salager, A. Rakhmatullin, C. P. Grey, L. Emsley and S. D. Stranks, J. Am. Chem. Soc., 2020, 142, 7813–7826 CrossRef CAS.
- X. Qiu, B. Cao, S. Yuan, X. Chen, Z. Qiu, Y. Jiang, Q. Ye, H. Wang, H. Zeng, J. Liu and M. G. Kanatzidis, Sol. Energy Mater. Sol. Cells, 2017, 159, 227–234 CrossRef CAS.
- T. Leijtens, R. Prasanna, A. Gold-Parker, M. F. Toney and M. D. McGehee, ACS Energy Lett., 2017, 2, 2159–2165 CrossRef CAS.
- D. Ricciarelli, D. Meggiolaro, F. Ambrosio and F. De Angelis, ACS Energy Lett., 2020, 5, 2787–2795 CrossRef CAS.
- M. I. Saidaminov, I. Spanopoulos, J. Abed, W. Ke, J. Wicks, M. G. Kanatzidis and E. H. Sargent, ACS Energy Lett., 2020, 5, 1153–1155 CrossRef CAS.
- J. Pascual, D. Di Girolamo, M. A. Flatken, M. H. Aldamasy, G. Li, M. Li and A. Abate, Chem.–Eur. J., 2022, 28, 1–7 Search PubMed.
- C. Ge, B. Jiang, J. Zhu, P. Zhang, R. Ma, S. Yan, Z. Liu, A. Shaker, M. S. Salem, J. Luo, L. Xu, J. K. Yang, Z. Li, H. Song, C. Chen and J. Tang, Adv. Funct. Mater., 2024, 2400075, 1–8 Search PubMed.
- A. Singh, J. Hieulle, J. F. Machado, S. Gharabeiki, W. Zuo, M. U. Farooq, H. Phirke, M. Saliba and A. Redinger, Nano Lett., 2022, 22, 7112–7118 CrossRef CAS PubMed.
- Z. Dai, T. Lv, J. Barbaud, W. Tang, T. Wang, L. Qiao, H. Chen, R. Zheng, X. Yang and L. Han, Sci. China Mater., 2021, 64, 2645–2654 CrossRef CAS.
- X. Liu, Y. Wang, T. Wu, X. He, X. Meng, J. Barbaud, H. Chen, H. Segawa, X. Yang and L. Han, Nat. Commun., 2020, 11, 1–7 CrossRef.
- M. Abbasli, J. Hieulle, J. Schrage, D. Wilks, A. Samad, U. Schwingenschlögl, A. Redinger, C. Busse and R. Ohmann, Adv. Funct. Mater., 2024, 34(40), 2403680 CrossRef CAS.
- N. H. Nickel, F. Lang, V. V. Brus, O. Shargaieva and J. Rappich, Adv. Electron. Mater., 2017, 3, 1–9 Search PubMed.
- J. Hieulle, A. Krishna, A. Boziki, J. N. Audinot, M. U. Farooq, J. Ferreira Machado, M. Mladenović, H. Phirke, A. Singh, T. Wirtz, A. Tkatchenko, M. Graetzel, A. Hagfeldt and A. Redinger, Energy Environ. Sci., 2024, 17, 284–295 RSC.
- J. Yang, Q. Hong, Z. Yuan, R. Xu, X. Guo, S. Xiong, X. Liu, S. Braun, Y. Li, J. Tang, C. Duan, M. Fahlman and Q. Bao, Adv. Opt. Mater., 2018, 6, 1–8 Search PubMed.
- X. Tang, M. Brandl, B. May, I. Levchuk, Y. Hou, M. Richter, H. Chen, S. Chen, S. Kahmann, A. Osvet, F. Maier, H. P. Steinrück, R. Hock, G. J. Matt and C. J. Brabec, J. Mater. Chem. A, 2016, 4, 15896–15903 RSC.
- W. C. Lin, W. C. Lo, J. X. Li, Y. K. Wang, J. F. Tang and Z. Y. Fong, npj Mater. Degrad., 2021, 5, 1–6 CrossRef.
- S. Svanström, A. García Fernández, T. Sloboda, T. J. Jacobsson, H. Rensmo and U. B. Cappel, Phys. Chem. Chem. Phys., 2021, 23, 12479–12489 RSC.
- L. Huerta Hernandez, M. A. Haque, A. Sharma, L. Lanzetta, J. Bertrandie, A. Yazmaciyan, J. Troughton and D. Baran, Sustainable Energy Fuels, 2022, 6, 4605–4613 RSC.
- C. Li, Z. Song, C. Chen, C. Xiao, B. Subedi, S. P. Harvey, N. Shrestha, K. K. Subedi, L. Chen, D. Liu, Y. Li, Y. W. Kim, C. s. Jiang, M. J. Heben, D. Zhao, R. J. Ellingson, N. J. Podraza, M. Al-Jassim and Y. Yan, Nat. Energy, 2020, 5, 768–776 CrossRef CAS.
- A. F. Akbulatov, S. A. Tsarev, M. Elshobaki, S. Y. Luchkin, I. S. Zhidkov, E. Z. Kurmaev, S. M. Aldoshin, K. J. Stevenson and P. A. Troshin, J. Phys. Chem. C, 2019, 123, 26862–26869 CrossRef CAS.
- J. Sanchez-Diaz, R. S. Sánchez, S. Masi, M. Kreĉmarová, A. O. Alvarez, E. M. Barea, J. Rodriguez-Romero, V. S. Chirvony, J. F. Sánchez-Royo, J. P. Martinez-Pastor and I. Mora-Seró, Joule, 2022, 6, 861–883 CrossRef CAS.
- J. H. Scofield, J. Electron Spectrosc. Relat. Phenom., 1976, 8, 129–137 CrossRef CAS.
- S. Hofmann, Auger- and X-Ray Photoelectron Spectroscopy in Materials Science: A User-Oriented Guide, 2013 Search PubMed.
- A. J. M. Prot, M. Melchiorre, F. Dingwell, A. Zelenina, H. Elanzeery, A. Lomuscio, T. Dalibor, M. Guc, R. Fonoll-Rubio, V. Izquierdo-Roca, G. Kusch, R. A. Oliver and S. Siebentritt, APL Mater., 2023, 11, 1–11 Search PubMed.
- T. Gallet, R. G. Poeira, E. M. Lanzoni, T. Abzieher, U. W. Paetzold and A. Redinger, ACS Appl. Mater. Interfaces, 2021, 13, 2642–2653 CrossRef CAS.
- E. M. Lanzoni, T. Gallet, C. Spindler, O. Ramírez, C. K. Boumenou, S. Siebentritt and A. Redinger, Nano Energy, 2021, 88, 106270 CrossRef CAS.
- T. Hellmann, M. Wussler, C. Das, R. Dachauer, I. El-Helalya, C. Mortan, T. Mayer and W. Jaegermann and We, J. Mater. Chem. C, 2019, 7, 5324–5332 RSC.
- T. Kirchartz, J. A. Márquez, M. Stolterfoht and T. Unold, Adv. Energy Mater., 2020, 1904134, 1–21 Search PubMed.
- Y. Takahashi, H. Hasegawa, Y. Takahashi and T. Inabe, J. Solid State Chem., 2013, 205, 39–43 CrossRef CAS.
- R. H. Petrucci, F. G. Herring, J. D. Madura and C. Bissonnette, General Chemistry: Principles and Modern Applications, 2017 Search PubMed.
- S. Tanuma, C. J. Powell and D. R. Pen, Surf. Interface Anal., 1994, 21, 165–176 CrossRef CAS.
- R. Wasylishen, O. Knop and J. B. Macdonald, Solid State Commun., 1985, 56, 581–582 CrossRef CAS.
- A. M. Leguy, J. M. Frost, A. P. McMahon, V. G. Sakai, W. Kochelmann, C. Law, X. Li, F. Foglia, A. Walsh, B. C. O'Regan, J. Nelson, J. T. Cabral and P. R. Barnes, Nat. Commun., 2015, 6, 1–3 Search PubMed.
- K. Fykouras, J. Lahnsteiner, N. Leupold, P. Tinnemans, R. Moos, F. Panzer, G. A. de Wijs, M. Bokdam, H. Grüninger and A. P. Kentgens, J. Mater. Chem. A, 2023, 11, 4587–4597 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta06361a |
| This journal is © The Royal Society of Chemistry 2025 |