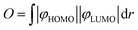Strongly fluorescent spiro-type tetracoordinate complexes of dibenzo[b,e][1,4]thiaborinine dioxide with functionalized 2-(benzo[d]heterazol-2-yl)phenolate ligands displaying TADF

Abstract

A series of eight luminescent tetracoordinate organoboron chelate complexes 7a–7d and 8a–8d, featuring spiro geometry of the boron centre, were synthesized by combining strongly electron-acceptor dibenzo[b,e][1,4]thiaborinine 5,5-dioxide (SO2B) with 2-(benzo[d]heterazol-2-yl)phenolate ligands comprising an attached 3,6-bis(tert-butyl)carbazole as a strong electron donor. Two analogous reference systems 9 and 10 bearing BF₂ and BAr₂ (Ar = 2,6-F₂-C₆H₃) cores, respectively, were also prepared and characterized. The obtained complexes exhibit bright blue, green or yellow photoluminescence in solution and Zeonex thin films with quantum yields reaching unity in some systems. Our detailed photophysical analysis of these complexes indicates the presence of thermally activated delayed fluorescence (TADF). Time-resolved photoluminescence experiments performed at RT and 77 K show that the energy difference between the lowest excited singlet and triplet states (ΔE_ST) is in the range of 0.22–0.36 eV. The most effective TADF emitters 7a and 7b were selected as luminescent dopants in OLEDs, showing external quantum efficiency (EQE) of up to 6.7% for the 7a-based device and maximum luminance of up to 9400 cd m⁻² for the 7b-based device.

---

1. Introduction

Organoboron compounds constitute an important group of luminescent systems with a strong potential as emitters in OLEDs. Among them, three-coordinate boron compounds, exhibiting inherent π-electron-acceptor character resulting from the presence of the vacant 2p orbital, were employed for that purpose.¹ In such systems, the effective p–π conjugation facilitates intramolecular charge transfer (ICT).² In many cases, their intense emission was ascribed to thermally activated delayed fluorescence (TADF) enabling construction of OLEDs featuring high EQE and luminance values.^3,4 Recently, multiple resonance (MR) MR-TADF emitters attracted a significant attention as they outperform traditional D–A TADF systems due to narrowband and tunable emission enabling construction of OLEDs with high colour purity.^5–10 Selected tetracoordinate organoboron compounds have also been studied as emitters in OLEDs.¹¹ Clearly, the electronic saturation of the boron atom in tetracoordinate organoboron compounds is increased and thus it cannot be considered as an acceptor centre per se. Yet, the boron atom can still significantly modulate the electronic density distribution in its vicinity, e.g., in aromatic chromophore chelating ligands (O,O–, O,N–, and N,N–) that are frequently used as key moieties responsible for emissive properties of respective complexes.^12–15 In most cases, those compounds exhibit conventional fluorescence although there are examples of simple boracyclic quinolates where the delayed fluorescence resulting from triplet–triplet annihilation was observed^16,17 whilst for other, related compounds the exact nature of this emission remains debatable.¹⁸ However, some tetracoordinate organoboron compounds with diverse structural architecture and spatial arrangement of the boron atom have been unambiguously determined as TADF emitters harvesting triplet excitons due to relatively low ΔE_ST values.¹⁹ As for three-coordinate boron TADF emitters, this is typically achieved by a proper structural design involving separation of HOMO and LUMO orbitals. For this purpose, the popular electron donors, including diphenylamine, carbazoles, 9,9-dimethyl-9,10-dihydroacridine, phenothiazine, and others, are attached to the central fragment of the molecule, i.e., a ligand and the chelated boron atom. The reported examples of TADF emitters often comprise the BF₂ moiety chelated with functionalized 2-(2-pirydyl)phenolates,^20,21 2-(5-aryl-1,3,4-oxadiazol-2-yl)phenolates,²² 2,2′-bipyridine-6,6′-bis(butylamide)²³ and selected β-diketonates.²⁴ A series of strongly emissive BF-based derivatives with 2,2′-(pyridine-2,6-diyl)diphenolate ligands were also reported.²⁵ Furthermore, chiral spiro type diolatoboron diketonates bearing pendant acridine units (D–π–A–π–D architecture) were shown to exhibit TADF with photoluminescence in the near infrared region.²⁶ A series of diarylborinic 2-(2-pirydyl)phenolates where the aryl groups possess an electron rich character due to appropriate functionalization have also been reported. Specifically, a donor-spiro-acceptor complex comprising the boracyclic azaborin core displayed high performance TADF with ΔE_ST approaching zero.¹⁴ TADF was also observed for other azaborin and thiaborin phenylpyridinato^27,28 and pyridylpyrrolide complexes.²⁹ Finally, two systems comprising a tetracoordinated organoboron acceptor bearing C^N^C chelate with attached donor moieties, i.e., phenoxazine and 9,9-dimethyl-9,10-dihydroacridine, were reported as relatively efficient emitters.³⁰

In this work, the recently introduced strongly electron-acceptor heteraborin scaffold SO2B³¹ was combined with four 2-(benzo[d]heterazol-2-yl)phenolate ligands decorated with 3,6-bis(tert-butyl)carbazole (TBCZ) as a donor moiety giving rise to a series of highly coloured and strongly luminescent chelate complexes featuring spiro geometry of the four-coordinated boron centre (Fig. 1). Characterization of the photophysical properties of these compounds was performed followed by utilising the two most promising structures as emitters in OLEDs.

Fig. 1 Molecular design of benzoheteroazole-SO2B complexes.

2. Materials and methods

2.1 Optical properties

The UV-vis absorption spectra were recorded using a Hitachi UV-2300II spectrometer. The emission spectra of solutions were recorded using Edinburgh FS5 equipped with an enhanced range photomultiplier detector (PMT-EXT). The measurements were performed at room temperature, according to published procedures.^32,33 Suprasil quartz cuvettes (10 mm) were used. 1.5 nm slit widths were used for absorption and emission spectra. To eliminate any background emission, spectrum of pure solvent was subtracted from the recorded spectra. Photoluminescence quantum yields were determined in diluted solutions (A ≈ 0.03 at the excitation wavelength used) by comparison with known standards – Coumarin 153 in ethanol (QY = 0.544). The concentration of all samples was adjusted to reach similar absorbance to the absorbance of the reference solution at the excitation wavelength. Thin films in Zeonex were deposited from toluene solutions through spin-coating and dried under vacuum at RT. Photoluminescence decays and time-resolved photoluminescence spectra in film were recorded using nanosecond gated luminescence and lifetime measurements (from 400 ps to 1 s) using the third harmonic (355 nm) of a high-energy pulsed Nd:YAG laser (EKSPLA). The emitted light was focused onto a spectrograph and detected with a sensitive gated iCCD camera (Stanford Computer Optics) having sub-nanosecond resolution.³⁴ Further details are available from an earlier work.³⁵ Temperature-dependent experiments were conducted using a liquid nitrogen cryostat VNF-100 (sample in flowing vapour, Janis Research) under nitrogen atmosphere.

2.2 Crystallographic studies

Single crystals of complexes 7d, 8a, 8b and 8d were prepared by slow evaporation of corresponding DCM solutions at RT. All crystals were measured at 100 K on a SuperNova diffractometer equipped with Atlas detector (Cu-K_α radiation, λ = 1.54184 Å) and Oxford Cryosystems nitrogen gas-flow device. The crystal structures were established in a conventional way via X-ray data refinement employing the Independent Atom Model (IAM). Data reduction and analysis were carried out with the CrysAlisPro suites of programs.³⁶ All structures were solved by direct methods using SHELXS-97³⁷ and refined using SHELXL-2016.³⁸ All non-hydrogen atoms were refined anisotropically. All carbon-bound hydrogen atoms were placed in calculated positions with the C–H distances of 0.95 Å and U_iso(H) = 1.2U_eq(C). The data quality of crystal structure 7d is low resulting in low bond precision, high R₁ and wR₂ values, and GooF deviating from unity. Nevertheless, the obtained structure unambiguously confirms the positions and connections between atoms. All-important crystallographic data including measurement, reduction, structure solution and refinement details are placed in Table S1.3 in the ESI.†

2.3 Theoretical calculations

Theoretical calculations were performed using Gaussian16 program.³⁹ Molecules were optimized using B3LYP^40–43 functional with 6-311++G(d,p) basis set.⁴⁴ The starting geometries were adopted from corresponding crystal structures 7d, 8a, 8b and 8d. For the remaining systems (7a–c, 8c, 9, 10), the molecular geometries were built in GaussView.⁴⁵ Following geometry optimization, the vibrational frequencies were calculated and the results showed that optimized structures are stable geometric structures. In optimization processes, no symmetry constraints were applied. Excited singlet and triplet state geometries for 7a and 7b were generated with TD-DFT methods starting from ground-state optimized geometries. TD-DFT calculations were performed at PBE0⁴⁶ level of theory (6-311++G(d,p) basis set) using CPCM continuum solvation model (toluene).⁴⁷ We have also tested M06-2X, B3LYP, CAM-B3LYP and ωB97XD functionals, however PBE0 functional provided the most consistent result with the experiment. Natural transition orbitals (NTO) were calculated for each excited state.⁴⁸ The MOs and NTOs were visualized with the Avogadro programme.⁴⁹ The overlap integrals (O) between HOMO and LUMO orbitals (HONTO and LUNTO for S₁ and T₁ states of 7a) were calculated with Multiwfn software (version 3.7)⁵⁰ according to the formula:
The spin–orbit coupling values for 7a and 7b were calculated with ORCA5.0.1 software.⁵¹

2.3.1 OLEDs. OLEDs were fabricated by vacuum thermal evaporation. Pre-patterned indium–tin-oxide (ITO) coated glass substrates with a sheet resistance of 20 Ω cm⁻² and ITO thickness of 100 nm were first washed with acetone and then sonicated in acetone and isopropanol for 15 min each time. Substrates were dried using an air gun and transferred into an oxygen-plasma generator for 6 min at full power. HAT-CN – dipyrazino[2,3-f:2′,3′-h]quinoxaline-2,3,6,7,10,11-hexacarbonitrile (sublimed, LUMTEC); TSBPA – 4,4′-(diphenylsilanediyl)bis(N,N-diphenylaniline) (sublimed, LUMTEC); mCP – 1,3-bis(carbazol-9-yl)benzene (sublimed, LUMTEC); PO-T2T – 2,4,6-tris[3-(diphenylphosphinyl)phenyl]-1,3,5-triazine (LUMTEC); TPBi – 1,3,5-tris(1-phenyl-1H-benzimidazol-2-yl)benzene, (sublimed, LUMTEC); LiF (99.995%, Sigma Aldrich); Al pellets (99.9995%, Lesker) were purchased from the companies indicated in parentheses. All device layers were thermally evaporated using a Kurt J. Lesker Spectros II deposition system at 10⁻⁶ mbar base pressure. All organic materials and aluminium were deposited at a rate of 1 Å s⁻¹. LiF layers, as well as 2 nm mCP layers were deposited at a rate of 0.1–0.2 Å s⁻¹. Characterisation of OLED devices was conducted in a 10 inch integrating sphere (Labsphere) connected to a Source Measure Unit (SMU, Keithley) and coupled with a spectrometer USB4000 (Ocean Optics). Further details are available in ref. 52. Devices of 4 × 2 mm pixel size were fabricated.

3. Results and discussion

3.1 Synthesis

The general idea of our molecular design is based on the HOMO vs. LUMO spatial separation. Thus, the donor TBCZ moiety is attached at the 4- or 5-position of the electron-rich phenolate moiety. In the first step, the Ullmann-type Cu(I)-catalyzed coupling of 4- or 5-bromo-2-methoxybenzaldehyde with TBCZ afforded the respective products 1 and 2 (Scheme 1).⁵³ They were converted into functionalized salicylaldehydes 3 and 4⁵⁴ followed by oxidative condensation with ortho-substituted anilines (X = NMe, NPh, O, S)⁵⁵ giving rise to 4 pairs of 2-(benzo[d]heterazol-2-yl)phenols as proligands 5a–5d and 6a–6d. The targeted complexes 7a–7d, 8a–8d were successfully obtained using mechanochemical approach involving liquid assisted grinding (LAG, PhMe as solvent)⁵⁶ of a respective proligand with 10-hydroxy-10H-dibenzo[b,e][1,4]thiaborinine 5,5-dioxide (SO2BOH). The synthesis of this boracyclic precursor was reported by us previously.³¹ In addition, reference complexes 9 and 10, i.e., analogues of 7a comprising BF₂ and BAr₂ (Ar = 2,6-F₂C₆H₃) moieties, respectively, were obtained. The yields of individual steps usually exceeded 70% whilst the total yields for the presented four-step protocols were in the range of ca. 15–40%.

Scheme 1 Synthesis of complexes 7a–7d and 8a–8d and reference systems 9 and 10.

The obtained complexes 7a–7d, 8a–8d exhibit long-term stability under ambient conditions. They also demonstrate high photostability, as they remain resilient to the continuous irradiation with 365 nm, 26 W LED strip light for several hours. According to DSC and TGA analyses, all complexes are characterized by high thermal stability (Table S5.1 and Fig. S5.1–S5.10, ESI†). Specifically, compounds 7a and 7b show superior thermal stability with decomposition occuring above 350 °C, whereas complexes 8b and 8c remain stable even up to 450 °C. For 7d, 8a and 8b thermogravimetric analysis revealed gradual mass loss up to 3–5% in the temperature range of 150–250 °C, which can be attributed to the evaporation of residual solvents. In addition, DSC curves recorded for complexes 7b and 7c show an apparent monotropic phase transitions occurring close to the melting point. For 8c, an exothermic peak, according to TGA not associated with mass loss, was observed at ca. 275 °C. This behaviour can be expected due to the conformational lability of the SO2B core (as discussed in crystallographic part), which generally promotes the occurrence of polymorphic forms.⁵⁷ In contrast to complexes 7a–7d and 8a–8d, the BAr₂ analogue 10 is characterized by lower stability as it is slowly hydrolysed by small amounts of water in organic solvents. This underscores the important role of the SO2B moiety, which forms stronger bonds with chelate ligands due to improved Lewis acidity of boron atom enhanced by the strongly electron-accepting properties of the sulfone group.

3.2 Crystal structures

The crystal structures of 7d, 8a, 8b and 8d were determined using single-crystal X-ray diffraction. The molecular structures are presented in Fig. 2a. All chelate complexes exhibit tetrahedral spiro geometry around boron atom with B–N bond lengths ranging from 1.58 to 1.62 Å, B–C bond lengths ranging from 1.58 to 1.66 Å and B–O bond lengths oscillating near 1.50 Å (Table S1.1, ESI†). Similar values were found in related organoboron complexes.^11,58,59 The comparative analysis of molecular geometries revealed that two heterocyclic rings bound by the central boron node display substantial conformational lability (Fig. 2b). The thiaborinine dioxide ring adopts chair conformation with two side aromatic rings significantly deviating from planarity. For most systems, the angle defined by the two SO2B aromatic ring planes (γ₁) is close to 162° (Table 1). In addition, the central thiaborinine dioxide ring loses its initial C₂ symmetry which is manifested by the deviation of α₁ angle defined by B1, S1 and O1/O2 atoms (Fig. 2c) from the ideal 120°. In turn, the six-membered OBN heterocyclic ring adopts half-chair conformation with boron atom significantly deviating out of the ligand plane by ca. d₁ = 0.5 Å. The magnitude of molecular distortions is similar between studied systems except for 8a, in which the distortion of the SO2B moiety is more significant (γ₁ = 143°, α₁ = 27°). This is, however, partially counterbalanced by a smaller distortion of the OBN heterocycle (d₁ = 0.409 Å). In addition, the ligand itself is not entirely flat as benzoazole and phenolato moieties are twisted along the C–C bond (torsion angle γ₂, Table 1). It should be stressed that such deviations may weaken the delocalization of electrons within the ligand affecting the photophysical properties of these systems.⁵⁵ Finally, in all studied complexes the carbazole moiety is twisted around the C–N bond by 45–55° (torsion angle γ₃, Table 1).

Fig. 2 (a) The molecular structures of 7d, 8a, 8b and 8d. Thermal motions are given as ADPs at the 50% probability level. Hydrogen atoms are omitted for clarity. (b) Overlap of the molecular structures of studied complexes. In the case of 7d there are two molecules in the asymmetric part of the unit cell (abbreviated as 7d_A and 7d_B). (c) Definition of geometrical parameters describing the distortions within boracyclic rings.

Table 1 Comparison of geometrical parameters describing the molecular distortions in 7d_A, 7d_B, 8a, 8b and 8d

	7d_A	7d_B	8a	8b	8d
d 1/Å	0.526	0.573	0.409	0.562	0.490
α 1/°	9	15	27	14	17
γ 1/°	162	164	143	164	163
γ 2/°	10(1)	13(1)	4.6(3)	12.0(5)	12.9(2)
γ 3/°	51(1)	53(1)	54.6(3)	49.5(5)	45.8(2)

---

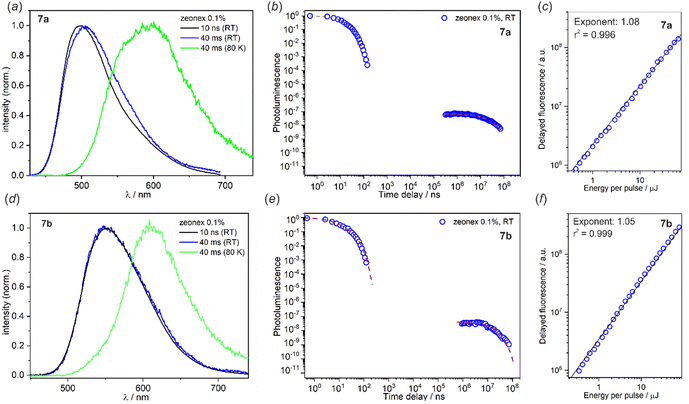
Crystal packing in all studied structures is dominated by weak C–H⋯C(π) and C–H⋯O intermolecular interactions, the latter contacts are mostly formed with oxygen atoms from the SO₂ group. The C(π)⋯C(π) interactions were found in structures 8a–8d, formed between adjacent carbazole units while π-stacking interactions involving benzoheteroazole moiety are rather avoided. This is mainly due to the presence of the perpendicularly aligned SO2B moiety which effectively prevents parallel approximation of benzoheteroazole planes. Exceptionally, the π-stacking was detected between phenyl groups in 8b (mean plane distance of 3.3 Å), but the parallel planes are significantly displaced with respect to each other thus this interaction is not optimal. The π-stacked carbazole units in 8a and 8d adopt head-to-tail orientation favoured by the strong dipole–dipole interactions and the vertical distances between carbazole mean planes are close to 3.6 Å. A different situation is observed in the crystal structure 8b, where two parallel carbazole units are distanced by 4.4 Å indicating that C(π)⋯C(π) interactions are less efficient. Instead, the carbazole units are held by C–H⋯C(π) interactions involving tert-butyl groups.

The analysis of the crystal structure of 7d shows that molecules are interconnected by multiple C–H⋯C(π) and C–H⋯O interactions. The most prominent crystal motifs involve 4 molecules of 7d to form a tetrameric assembly through C–H⋯O interactions with SO₂ oxygen atoms (Fig. 3). In the case of 8a, the molecules are interconnected by two pairs of cooperative C–H⋯C(π) and C–H⋯O interactions. Besides, the molecules are involved in two types of dimeric motifs arising from C–H⋯C(π) interactions formed between benzoheteroazole C–H proton and π-electron density from the neighboured dibenzothiaborinine dioxide group. Propagation of these two centrosymmetric dimeric motifs along the [101] direction leads to formation of an infinite one-dimensional molecular chain (Fig. 3). The further connections between chains are realized by relatively strong C–H⋯O interactions with sulfone groups. In the case of 8d, the characteristic crystal motif involves tetrameric assembly formed by two pairs of π-stacked dimers connected with each others via C–H⋯C(π) and C–H⋯O interactions. Besides that, the structure features two types of centrosymmetric dimers which are held by relatively strong C–H⋯C(π) interactions formed with C–H protons belonging to the N-phenyl or SO2B group, both sandwiching benzoimidazole moiety.

Fig. 3 Fragments of crystal structures showing the main structural motifs in 7d, 8a, 8b and 8d. Hydrogen atoms were omitted for clarity.

3.3 Cyclic voltammetry

The electrochemical properties of all complexes were analyzed based on corresponding half wave potentials (oxidation – E^1/2_ox and reduction – E^1/2_red) obtained using cyclic voltammetry (CV) measurements in CH₂Cl₂ and were reported with respect to the FeCp₂/FeCp₂⁺ redox couple. For irreversible redox processes, the potentials were estimated based on the onset values. The CV plots are shown in the ESI† (Fig. S4.1–S4.2), and the data are summarized in Table 2. All complexes display reversible or quasi-reversible first oxidation waves, while the reduction processes are essentially irreversible with some exceptions for benzothiazole derivatives 7b and 8b. The oxidation potentials are in the range 0.68–0.85 V. They are systhematically lower by ca. 0.1 V for 7a–7d compared to analogous compounds from the series 8a–8d. For the former, the second, irreversible oxidation waves are observed in the range 1.04–1.19 V. The reduction potentials span in a rather wide range, i.e., between −1.82 for 7b and −2.26 V for 8c. Thus, respective electrochemical energy gaps vary in the range of 2.56–3.04 eV and are consistent with optical energy gaps spanning in the range of 2.42–2.94 eV, in line with the energy of the HOMO–LUMO transitions. Comparison of the data concerning all analogous pairs from series 7a–7d and 8a–8d reveals that both electrochemical and optical energy gaps are lower in the former systems by 0.07–0.19 eV. For 9 and 10, the E^1/2_ox values are very similar to those for the analogue 7a. As for 7a, a second irreversible oxidation wave was also observed for 10. However, it was absent for 9, which may indicate that it is associated with oxidation of the B–Ar moieties. The E^1/2_red values for 9 and 10 are lower by ca. 0.15 V compared to 7a, which indicates that the introduction of the SO2B moiety results in a relative decrease of the LUMO energy consistent with a strong electron-acceptor ability of this boracyclic core.

Table 2 Redox potentials, HOMO and LUMO energy levels and energy gaps for studied complexes based on CV measurements (ΔE^CV), UV-vis absorption data (ΔE^Abs) and theoretical calculations at the B3LYP/6-311++G(d,p) level of theory (ΔE^DFT). All potentials are given with respect to the FeCp₂/FeCp₂⁺ redox couple

	Cyclic voltametry					UV-vis	DFT
	E ^1/2red/V	E ^1/2ox/V	HOMO^d/eV	LUMO^e/eV	ΔE^CV/eV	ΔE^Abs/eV	HOMO/eV	LUMO/eV	ΔE^DFT/eV
a First oxidation potential. b Second oxidation potential, estimated from onset values. c Second oxidation not recorded within the electrochemical window. d HOMO = −(E^1/2ox + 4.8 eV). e LUMO = −(E^1/2red + 4.8 eV).
7a	−1.95	0.75^a/1.19^b	−5.55	−2.85	2.70	2.57	−5.66	−2.73	2.93
7b	−1.82	0.74^a/1.14^b	−5.54	−2.98	2.56	2.42	−5.66	−2.90	2.75
7c	−2.21^a	0.70^a/1.05^b	−5.50	−2.59	2.91	2.81	−5.68	−2.40	3.28
7d	−2.16^a	0.68^a/1.04^b	−5.48	−2.64	2.84	2.72	−5.64	−2.35	3.29
8a	−1.92^a	0.85^a/—^c	−5.65	−2.88	2.77	2.76	−5.71	−2.67	3.04
8b	−1.88	0.81^a/—^c	−5.61	−2.92	2.69	2.59	−5.70	−2.83	2.87
8c	−2.26^a	0.78^a/—^c	−5.58	−2.54	3.04	2.94	−5.69	−2.31	3.38
8d	−2.20^a	0.80^a/—^c	−5.60	−2.60	3.00	2.90	−5.64	−2.26	3.38
9	−2.11	0.73^a/—^c	−5.53	−2.69	2.84	2.67	−5.63	−2.70	2.93
10	−2.10	0.73^a/1.21^b	−5.53	−2.70	2.83	2.67	−5.49	−2.51	2.98

---

3.4 Steady-state spectroscopy in solution

UV-vis absorption and emission spectra of 7a–7d and 8a–8d were measured in toluene (PhMe), dichloromethane (DCM), and acetonitrile (MeCN). The results are collected in Table 3 and the corresponding spectra are presented in Fig. 4 (PhMe) and Fig. S2.1–S2.10 (DCM, MeCN) in the ESI.† Overall, the UV-vis absorption spectra of 7a–7d show strong bands in the range of ca. 330–360 nm featuring vibronic structure as well as weaker broad structureless bands with maxima in the range of 390–451 nm. For 8a–8d there are very intense bands with distinctive vibronic structures spanning in the range of 320–456 nm. Our results show that the respective longest-wavelength absorption maxima are only slightly dependent on the position of the TBCZ moiety, i.e. the difference does not exceed 10 nm between the two groups of luminophores. In contrast, the intensity of this band is much lower for 7a–7d than for 8a–8d (Fig. S2.11, ESI†). In addition, absorption spectra recorded in solvents of varying polarity reveal a relatively modest negative solvatochromic effect in both groups of luminophores (Fig. S1–S8, ESI†).

Table 3 UV-vis absorption and emission data for 7a–7d, 8a–8d in solution

	Solvent	λ abs/nm (ε/10^3 dm^3·mol^−1·cm^−1)	λ ex/nm	λ em/nm	Δ/cm^−1	QY^a
a Measured under air-equilibrated conditions.
7a	PhMe	332 (10.8); 344 (11.5); 424 (3.5)	420	522	4430	0.51
	DCM	345 (13.0); 417 (5.0)	420	555	5960	0.38
	MeCN	332 (10.8); 345 (11.5); 404 (4.9)	405	578	7450	0.03
7b	PhMe	346 (9.5); 365 (6.1); 451 (4.0)	450	565	4470	0.48
	DCM	373 (7.1); 440 (5.1)	440	590	5780	0.33
	MeCN	345 (9.6); 367 (6.0); 425 (4.6)	420	619	7370	0.03
7c	PhMe	332 (14.6); 390 (6.5)	383	476	4630	0.64
	DCM	334 (17.9); 344 (17.0); 388 (8.6)	383	492	5450	0.66
	MeCN	332 (14.6); 344 (12.5); 378 (7.7)	383	498	6370	0.30
7d	PhMe	333 (12.3); 406 (5.3)	405	497	4510	0.67
	DCM	334 (12.2); 345 (11.7); 405 (5.3)	405	508	5010	0.69
	MeCN	333 (12.3); 344 (11.0); 394 (5.5)	393	518	6080	0.32
8a	PhMe	328 (7.9); 344 (10.5); 379 (20.5); 411 (34.1); 427 (39.3)	426	489	2970	0.40
	DCM	343 (8.2); 406 (35.7); 421 (38.8)	405	545	5400	0.47
	MeCN	408 (33.2)	395	578	7210	0.07
8b	PhMe	341 (6.3); 391 (11.4); 437 (26.6); 456 (30.5)	435	514	2470	0.42
	DCM	342 (5.7); 445 (39.3)	427	573	5020	0.41
	MeCN	340 (7.4); 431 (42.8)	420	618	7020	0.04
8c	PhMe	331 (8.3); 387 (39.8); 400 (39.8)	383	436	2060	0.97
	DCM	331 (8.6); 347 (13.9); 383 (37.2); 398 (39.0)	388	479	4250	1.00
	MeCN	373 (33.5); 385 (34.0)	382	498	5890	0.71
8d	PhMe	331 (6.1); 346 (8.9); 392 (34.0); 410 (37.2)	392	457	2510	0.97
	DCM	330 (7.2); 346 (11.0); 388 (35.1); 403 (38.1)	382	492	4490	0.76
	MeCN	381 (34.5); 393 (36.0)	372	517	6100	0.47
9	PhMe	346 (14.8); 413 (5.8)	405	513	4720	0.12
	DCM	335 (14.4); 346 (15.8); 408 (6.3)	405	536	5850	0.09
	MeCN	334 (14.2) 345 (14.4); 400 (5.5)	405	559	7110	0.07
10	PhMe	334 (7.3); 346 (7.87); 415 (2.8)	405	510	4490	0.57
	DCM	335 (8.6); 345 (8.8); 406 (3.4)	405	541	6150	0.41
	MeCN	333 (9,8); 344 (9.7); 396 (3.8)	405	574	7830	0.10

---

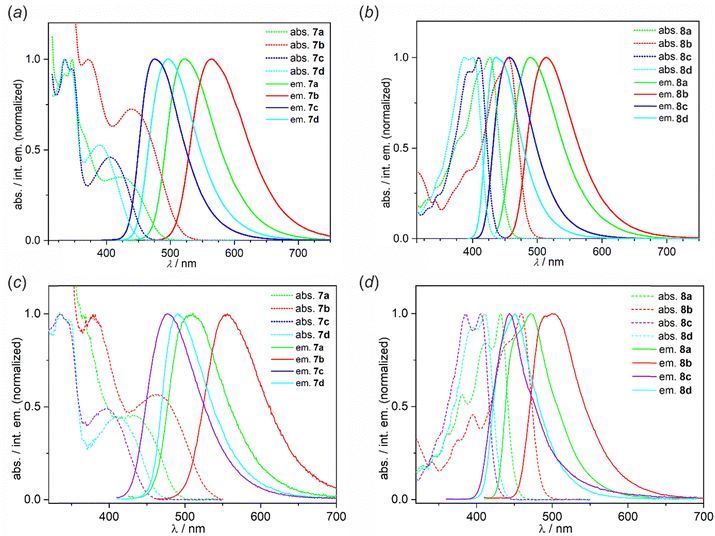Fig. 4 Normalized absorption and emission spectra of 7a–7d and 8a–8d in (a) and (b) dilute (c = 10⁻⁵ M) toluene solution and (c) and (d) Zeonex thin films (0.1 wt%) measured at RT. Excitation wavelengths are given in Table 3.

The emission color in toluene solutions spans from blue (8c: λ_em = 436 nm) to yellow (7b: λ_em = 565 nm). The Stokes shifts recorded for 7a–7d in toluene are larger than in 8a–8d indicating a stronger CT character with donor localised in the para rather than meta position to the B–O group. Thus, the photoluminescence maxima of complexes 7a–7d are shifted bathochromically with respect to complexes 8a–8d. All complexes show positive photoluminescence solvatochromism which is generally stronger for 8a–8d. We observe an important role of the benzoheterazole moiety on solvatochromism with benzoxazole and benzothiazole derivatives showing stronger effect than benzimidazole analogues. The type of the benzoheteroazole moiety is also critical for the PLQY values in MeCN. We observe that benzoxazole and benzothiazole derivatives 7a–7b and 8a–8b generally show a lower PLQY in this solvent than their benzimidazole analogues. In less polar solvents, i.e., PhMe and DCM, all compounds are moderate-to-strong emitters with QY reaching 1.00 for 8c in DCM despite the value being recorded in air-equilibrated conditions. This indicates prominent fluorescent properties of these emitters, but suggests relatively low contributions of TADF to the overall photoluminescence with the latter generally being quenched in the presence of oxygen. Furthermore, a comparison of the UV-vis absorption spectrum of 7a and its analogues 9 and 10 reveals that the replacement of the SO2B moiety with BF₂ or BAr₂ (Ar = 2,6-F₂C₆H₃) core, respectively, leads to only a slight (ca. 10 nm) hypsochromic shift of the lowest absorption bands as well as a similar shift of the emission spectra. Notably, the emission properties of reference system 9 are weak with QYs in the range of 0.07–0.12, whereas 10 behaves similarly to 7a with a QY of up to 0.57 in PhMe.

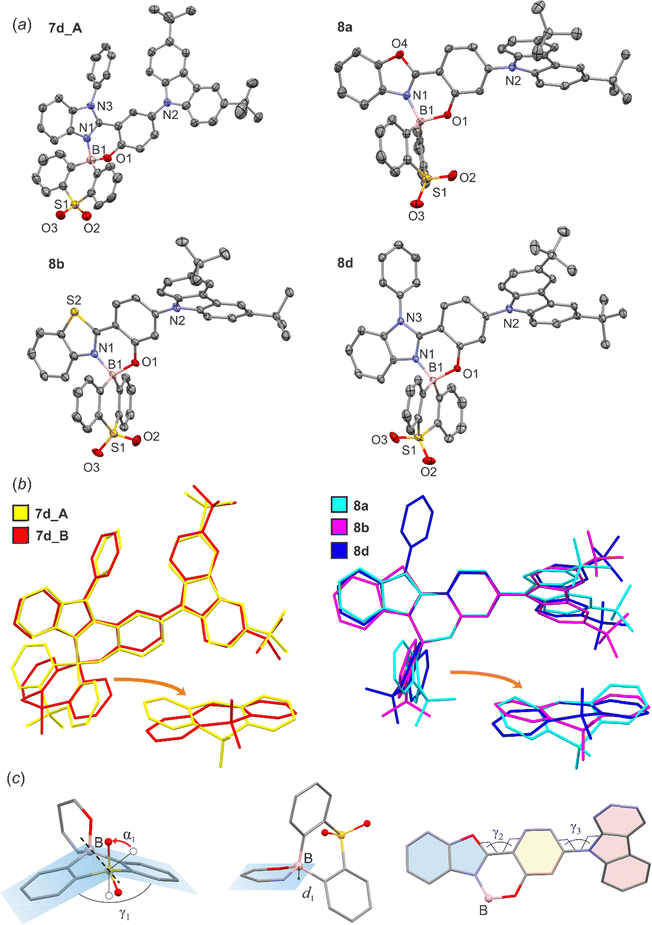
3.5 Optical properties in doped films

Steady state emission was also studied in 0.1 wt% Zeonex thin films at RT, showing respective photoluminescence spectra with maxima at slightly shorter or similar wavelengths to those recorded in toluene solutions (Fig. 4c and d). The QYs are generally high, in the range of 0.66–1.00 (Table 4). Apart from the steady-state photoluminescent characteristics presented above we have also used time-resolved techniques to gain a further insight into the properties of the studied boron complexes. Our results include photoluminescence decay traces recorded using an iCCD camera. Generally speaking, all studied boron complexes display TADF as they are characterised at RT by a short luminescent component in the nanosecond timescale and a long-lived component with a spectrum identical to that of the first component (Fig. 5). Typically for TADF, the delayed fluorescence signal disappears at 80 K with phosphorescence being present instead. In some of the complexes, i.e.7c, 7d and 8a–8d the phosphorescent component can still be observed even at RT, which suggests a relatively large ΔE_ST in these materials.⁶⁰ From the fluorescence and phosphorescence spectra it is possible to estimate the energy of the singlet and triplet states. The calculated energy difference between the singlet and triplet states (ΔE_ST) for series 7a–7d is in the range of 0.22–0.26 eV. For 8a–8d the ΔE_ST values are generally higher by ∼0.1 eV at 0.30–0.35 eV. This larger ΔE_ST in complexes 8a–8d is in line with stronger conjugation between carbazole and benzoheteroazole moieties in that group of complexes than in 7a–7d. The average PF lifetimes are in the range of 10.7–16.7 ns for 7a–7d and 2.6–4.1 ns for 8a–8d, in line with the strength of the lowest CT transition indicated from absorption spectra.⁶¹ On the other hand, the average TADF lifetimes are in the range of 14–74 ms for 7a–7d and 15–32 ms for 8a–8c, while we were unable to determine the TADF lifetime in 8d due to a very weak signal. We observe that the relative intensity of TADF and its lifetime visibly depends on the benzoheteroazole used. For example, the amplitude of TADF signal in 7a and 7b is about one order of magnitude larger than in 7c and 7d. Similarly, the average decay lifetime is visibly longer in the latter two complexes. This can be linked to an elongated T₁ state lifetime due to potentially slower triplet non-radiative decay, which is suggested by larger DF/PF values in this case. The same cannot be said about the analogous complexes 8a–8d. For luminophores 8a–8d the overall TADF amplitude is visibly lower than in respective complexes 7a–7d. Hence, 8a and 8b display a lower TADF amplitude than 7a and 7b, but for 8d the intensity is so low it is no longer possible to obtain its reliable TADF lifetime. The behaviour of reference complexes 9 and 10 is somewhat similar to that of 7a, with comparable ΔE_ST ≈ 0.20–0.27 eV, but longer TADF lifetime. Complexes 9 and 10 also display a larger DF/PF ratio than 7a, which together with longer TADF lifetimes may be indicative of reduced T₁ non-radiative decay.

Table 4 Photophysical data for studied complexes in 0.1% solid film in Zeonex

	λ F/nm	λ PH/nm	ΔEST/eV	E S/eV	E T/eV	τPF^a/ns	τDF^a/ms	QY^b	DF/PF
a Average lifetime τav = (A1τ1^2 + A2τ2^2)/(A1τ1 + A2τ2). b Degassed conditions. c Weak signal, not determined.
7a	510	562, 600	0.26	2.74	2.48	13.5 ± 0.3	20 ± 1	0.97	0.10
7b	545	610	0.24	2.51	2.27	16.7 ± 0.6	14 ± 1	1.0	0.07
7c	480	536	0.22	2.88	2.66	10.7 ± 0.1	56 ± 3	1.0	0.16
7d	492	535, 548	0.24	2.81	2.57	13.9 ± 0.2	74 ± 4	0.96	0.35
8a	474	509, 542	0.32	2.90	2.58	3.9 ± 0.2	34 ± 0.3 (95%); 1.2 ± 0.3 (5%)	0.79	0.04
							τ av = 32
8b	499	500, 538, 574	0.30	2.71	2.40	4.1 ± 0.1	18 ± 2 (87%); 1.2 ± 0.1 (13%)
							τ av = 16	0.66	0.07
8c	446	484, 509, 549	0.35	3.09	2.74	2.6 ± 0.1	15 ± 3	0.94	∼0.01
8d	448	487, 516	0.35	3.06	2.71	2.6 ± 0.1	—^c	0.86	—^c
9	484	544, 575	0.27	2.79	2.52	10.1 ± 0.3	39 ± 1	0.60	0.27
10	497	545, 575	0.20	2.73	2.53	12.5 ± 0.4	53 ± 3	0.98	0.24

---

Fig. 5 (a) and (d) Time-resolved prompt and delayed fluorescence (RT), and phosphorescence spectra (80 K) of 7a and 7b in Zeonex films. (b) and (e) Photoluminescence decay traces for 7a and 7b in Zeonex films at RT. (c) and (f) Relationship between the intensity of delayed fluorescence for 7a and 7b in 0.1% Zeonex films and excitation dose, presented in a double logarithmic scale.

Calculated k_PF, k_ISC, k_rISC, and Φ_rISC values in the Zeonex matrix are collected in Table S3.1 in the ESI.† The k_PF values generally agree with the trend set out by the PF lifetimes with complexes 7a–7d showing lower values, k_PF = 5.1–8.1 × 10⁷ s⁻¹, than 8a–8d, k_PF = 15.0–35.8 × 10⁷ s⁻¹. The k_rISC values range 16.4–76.4 s⁻¹ for 7a–7d and 5.2–11.4 s⁻¹ for 8a–8d. These are rather very small k_rISC values, reflecting the long >10 ms TADF lifetimes of these luminophores. Φ_rISC values for 7a–7d are generally close to unity, at 0.77–1.00, while for 8a–8d are visibly smaller, at 0.14–0.17. The trend in both k_rISC and Φ_rISC indicates a much more favourable conditions for efficient rISC in the former group. In this respect reference complexes 9 and 10 are similar to complexes 7a–7d.

To unequivocally rule out the possibility the discussed delayed fluorescence is of triplet–triplet annihilation (TTA) origin we used a very low emitter load at 0.1 wt%. Furthermore, we studied the dependence of the delayed fluorescence intensity upon excitation dose, finding that the relationship is linear (exponent ≈1) in all cases, which unambiguously confirmed the presence of TADF⁶² (Fig. S3.7–S3.9, ESI†).

Some of the above effects can be attributed to the relative magnitude of ΔE_ST. However, in the case of complexes studied in this work, one may not unequivocally assign all variations in TADF behaviour solely to ΔE_ST as other factors, such as T₁ and S₁ radiative rates also play a role in this case,⁶³ not to mention the effects of triplet non-radiative decay which are difficult to account for quantitatively in our case. For example, complexes 8a–8d display shorter fluorescence lifetimes than the 7a–7d which together with the generally high QY of the two groups of complexes allows to assign this behaviour to faster S₁ decay rates. Due to the competition between singlet decay and ISC this leads to lower triplet formation yields and hence lower relative TADF intensity in 8a–8d. Based on our results, we identified 7a and 7b as the most promising for use as emitters in OLEDs.

Finally, we have measured the emission properties for 7a and 7b at concentrations of 0.1, 1, 4, 7 (or 8) wt% in a solid state matrix. The higher concentrations were not available because of the limited solubility of the compounds in organic solvents such as chloroform or toluene. We have found that for both compounds the emission is bathochromically shifted as the concentration of the dopant increases (Fig. S2.14, ESI†). This is accompanied by the drop of the QY (Table S2.1, ESI†), which can be attributed to some aggregation effects. For 7a, the emission quenching occurs mostly in the concentration range of 1–4 wt% but QY remains high (86%) at 7 wt%. For 7b, the QY drops gradually in the concentration range of 0.1–4 wt% and then it remains essentially constant reaching the value of 61% at 8 wt%. Thus, it seems that the concentration of ca. 7–8 wt% represents an optimal balance offering relatively high number of emitting centers while maintaining effective performance.

3.6 Theoretical calculations

To support experimental findings, we have performed DFT (B3LYP/6-311++G(d,p)) and TD-DFT (PBE0/-311++G(d,p)) theoretical calculations using Gaussian16 software. To quantify the efficiency of HOMO and LUMO coupling, the overlap integrals (O) of ground and excited wavefunctions were calculated (Table S6.1, ESI†). The calculated absorption and emission wavelengths are in good agreement with the experimental values (Table S6.2, ESI†) and the oscillator strength values for the emission process are consistent with the values calculated using the Strickler–Berg approach (Table S2.2, ESI†).⁶¹ For compounds 7a and 7b, identified as the most efficient systems for OLED applications, we have also calculated singlet and triplet excited state levels, along with natural transition orbitals (NTOs) (Fig. S6.5 and S6.6, ESI†).

For all studied compounds the HOMO orbital is mainly located on the TBCZ with some contribution from the phenolate ring, while the LUMO spreads over the entire 2-(benzo[d]heterazol-2-yl)phenolate ligand core. Thus, the HOMO orbital partially overlaps with LUMO at the phenolate ring, and the magnitude of this effect strongly depends on the position of the TCBZ moiety and a degree of its twisting around the C–N bond (torsion angle γ₃, Table 1). In the case of 8a–8d (O = 0.42–0.43), the location of TCBZ at the para position with respect to benzoheteroazole acceptor leads to more efficient electron conjugation compared to 7a–7d (O = 0.26–0.29). This naturally correlates with their higher ΔE_ST values,⁶⁴ as well as with their general photophysical behaviour discussed earlier. The subsequent TD-DFT calculations on compounds 7a–7d revealed that the first electron excitations are predominately due to the HOMO–LUMO transition indicating a charge transfer character of S₁ state. This is also reflected by relatively low oscillator strength values for this transition (0.038–0.060). In contrast, in case of 8a–8d, the higher HOMO–LUMO overlap leads to much higher oscillator strength values (0.267–0.369).

The computed singlet–triplet energy differences for 7a and 7b (ΔE_ST = 0.27 eV for both compounds) are in a very good agreement with the experimental results, despite the absolute S₁ and T₁ energy values deviating from experimental results. Interestingly, the dipole moments of singlet excited states at the Franck–Condon geometry (S^FC₁) decrease with respect to ground electronic state (for 7a: μ(S₀) = 6.82 D, μ(S^FC₁) = 6.62 D; for 7b: μ(S₀) = 7.44 D; μ(S^FC₁) = 7.30 D). This rationalizes the hypsochromic shift in the absorption spectra in solvents of increasing polarity.¹⁷ With the subsequent geometry relaxation, the dipole moment increases surpassing the S₀ state (7a: μ(S₁) = 7.07 D, for 7b: μ(S₁) = 7.86 D;), which stays in agreement with the observed batochromic shift in emission spectra. The geometry relaxation results in twisting of the TCBZ-phenolate dihedral angle (γ₃) from 63.9° to 69.6° for 7a and from 63.7° to 74.5° for 7b, leading to a higher separation of the donor and acceptor moieties (Fig. 6). This phenomenon was observed in other compounds consisting of D and A components linked by a single bond.^65,66 The subsequent intersystem crossing to the T₁ state results in a decrease of γ₃ dihedral angle giving rise to a higher overlap between corresponding NTO orbitlals.

Fig. 6 (a) Energy diagram (B3LYP/6-311++G(d,p)) showing the absorption and prompt/delayed fluorescence (PF/DF) in 7a. Inset depicts changes in carbazole plane twisting angle. (b) HONTO and LUNTO for S₀, S₁ and T₁ states. The overlap integrals between HONTO and LUNTO were provided for each state.

The spin orbit couplings between S₁ and T₁ states (0.57 cm⁻¹ for 7a and 0.50 cm⁻¹ for 7b) are comparable to other TADF emitters. Thus rISC mechanism involves slow reverse internal conversion (rIC) as the T₂ state is energetically too high (>0.5 eV) above the T₁ (Fig. 6a). The S₁ and T₁ are potentially ca. 2 vibrations (0.14 eV each) apart which is consistent with several coupled vibrational modes. Thus, rISC occurs slowly at RT, which accounts for a very long DF lifetime.

3.7 OLED devices

Considering the prominent luminescent behaviour of complexes 7a and 7b and their TADF properties, we decided to prepare vacuum-deposited OLEDs featuring them as luminescent materials in the emissive layer. We used the OLED structure previously employed for other boron complexes which appears to universally suit a wide variety of boron luminophores.^16,31 The OLED architecture ITO|HAT–CN (10 nm)|TSBPA (40 nm)|mCP (2 nm)|mCP : PO–T2T (80 : 20) co 7% 7a/7b|PO–T2T (5 nm)|TPBi (40 nm)|LiF (0.8 nm)|Al (100 nm) features a blend emissive layer (EML) comprising both electron- and hole-transporting components. HAT–CN serves as the hole injection layer, while TSBPA as the hole transport layer. A thin (2 nm) layer of mCP is used as a spacer and a hole transport layer. A thin layer of PO–T2T serves as the hole blocking layer, while TPBi is the electron transport layer. LiF is the electron injection layer, while Al serves as a cathode. Electrical and electroluminescent characteristics of these OLEDs are summarised in Fig. 7, while the pertinent numerical data is collected in Table 5.

Fig. 7 Electroluminescent properties of OLEDs featuring 7a and 7b as emitters: (a) electroluminescence spectra; (b) EQE vs. current density; (c) current density vs. voltage; (d) luminance vs. voltage.

Table 5 Summary of electroluminescent properties of OLEDs featuring 7a and 7b as emitters

Device	V ON /V	λ EL /nm	L max /cd m^−2	CEmax^d/cd A^−1	EQEmax^e/%	CIE 1931 (x; y)^f
a Turn-on voltage at 5 cd m^−2. b Electroluminescence maxima. c Maximum luminance. d Maximum current efficiency. e Maximum external quantum efficiency. f Colour coordinates of electroluminescence as defined in International Commission on Illumination color space CIE 1931.
7a	4.1	519	4400	15.5	6.7	(0.27; 0.53)
7b	4.0	552	9400	14.1	5.8	(0.40; 0.53)

---

The two OLED structures can be identified through the respective emitting materials used: 7a or 7b. The devices display a moderate V_ON at ∼4 V and show green (7a) and yellow (7b) electroluminescence. They display very similar if not nearly identical electrical and electroluminescent characteristics with the divergent behaviour only visible above 100 mA cm⁻² where the 7a OLED shows a more significant efficiency roll-off. As a result the maximum luminance of 7a (4400 cd m⁻²) is lower than that of 7b (9400 cd m⁻²). The external quantum efficiency (EQE) of both OLEDs is comparable, at ∼6–7%, while the current efficiency is in the range of ∼14–16 cd m⁻², in line with TADF properties presented by these materials.

4. Conclusions

In conclusion, 8 chelate complexes composed of a novel strongly electron-acceptor boracyclic core SO2B and 4 types of 2-(benzo[d]heterazol-2-yl)phenolate ligands bearing a pendant 3,6-bis(tert-butyl)carbazole electron-donating moiety were obtained using a mechanochemical approach, and fully characterized by ¹H, ¹³C NMR, UV-vis spectroscopy, HRMS, and cyclic voltammetry. The structure of 4 compounds was determined by single crystal X-ray diffraction analysis. For comparison, two analogous complexes were obtained by replacing the SO2B core with the simple BF₂ group or its bulkier counterpart BAr₂ (Ar = 2,6-F₂C₆H₃). All complexes are luminescent both in solution and solid state. Further studies involving analysis of time-resolved emission spectra revealed the presence of TADF which was exploited in prototype OLEDs using complexes 7a and 7b. They showed a considerable efficiency (EQE of up to ca. 7%) whilst their emission colour was dependent on the type of the heteroatom in the heterazole ring. In this work, we introduce new tetracoordinate organoboron complexes displaying TADF, which are overall uncommon in respect to their three-coordinate counterparts such as the recently reported SO2B-Dipp-CZ where SO2B acts as a strong acceptor whilst carbazole (CZ) plays the role of a donor.³¹ As three-coordinate analogues generally show stronger electron-acceptor properties it is easier to achieve smaller ΔE_ST. For this particular reason, the TADF and OLED performance of SO2B-Dipp-CZ emitter is superior to 7a and 7b. However, the tetra-coordinate derivatives presented here lend themselves to an easier modification, allowing for facile production of multiple derivatives, as shown in this work. Clearly, more work is required to further enhance electron withdrawing properties of tetra-coordinate boron acceptors towards achieving smaller ΔE_ST and improved TADF performance. However, the results presented herein indicate that other related spiro-type tetracoordinate complexes may also be considered promising TADF emitters. It should be noted that their easy modular synthesis can potentially allow for obtaining a library of emitters with tunable characteristics.

Data availability

The data supporting this article have been included as part of the ESI.† Crystallographic data for 7a, 8a, 8b, 8d has been deposited at the CCDC under depositions no. 2352195 (7d), 2352196 (8a), 2352197 (8b) and 2352198 (8d) and can be obtained from https://www.ccdc.cam.ac.uk.

Conflicts of interest

The authors declare no potential conflict of interest.

Acknowledgements

This work was supported by the National Science Centre (Poland) within the framework of the project DEC-UMO-2023/49/B/ST5/00824. M. U. acknowledges The Iwanowska Programme funded by the Polish National Agency For Academic Exchange (NAWA). The authors thank Wroclaw Centre for Networking and Supercomputing (https://www.wcss.pl), grant no. 285, for providing computer facilities (Gaussian16). We also acknowledge the support by the Warsaw University of Technology. P. P. thanks Silesian University of Technology, Poland for funding under Rector's pro-quality grant no.: 04/040/RGJ24/0279.

References

1. H. Lee, D. Karthik, R. Lampande, J. H. Ryu and J. H. Kwon, Front. Chem., 2020, 8, 373.
2. L. Ji, S. Griesbeck and T. B. Marder, Chem. Sci., 2017, 8, 846–863.
3. L. Wan, Z. Cheng, F. Liu and P. Lu, Mater. Chem. Front., 2023, 7, 4420–4444.
4. J. Shi, Z. Ran, F. Peng, M. Chen, L. Li, L. Ji and W. Huang, J. Mater. Chem. C, 2022, 10, 9165–9191.
5. T. Hatakeyama, K. Shiren, K. Nakajima, S. Nomura, S. Nakatsuka, K. Kinoshita, J. Ni, Y. Ono and T. Ikuta, Adv. Mater., 2016, 28, 2777–2781.
6. H.-Z. Li, F.-M. Xie, Y.-Q. Li and J.-X. Tang, J. Mater. Chem. C, 2023, 11, 6471–6511.
7. C. Lv, X. Wang, Q. Zhang and Y. Zhang, Mater. Chem. Front., 2023, 7, 2809–2827.
8. M. Mamada, M. Hayakawa, J. Ochi and T. Hatakeyama, Chem. Soc. Rev., 2024, 53, 1624–1692.
9. F.-M. Liu, L.-Y. Ding, Y.-J. Yu, M.-T. Li, L.-S. Liao and Z.-Q. Jiang, J. Mater. Chem. C, 2023, 11, 11425–11439.
10. Y. Liu, X. Xiao, Y. Ran, Z. Bin and J. You, Chem. Sci., 2021, 12, 9408–9412.
11. D. Li, H. Zhang and Y. Wang, Chem. Soc. Rev., 2013, 42, 8416–8433.
12. A. C. Murali, P. Nayak and K. Venkatasubbaiah, Dalton Trans., 2022, 51, 5751–5771.
13. P. H. Marek-Urban, M. Urban, M. Wiklińska, K. Paplińska, K. Woźniak, A. Blacha-Grzechnik and K. Durka, J. Org. Chem., 2021, 86, 12714–12722.
14. B. M. Bell, T. P. Clark, T. S. De Vries, Y. Lai, D. S. Laitar, T. J. Gallagher, J.-H. Jeon, K. L. Kearns, T. McIntire, S. Mukhopadhyay, H.-Y. Na, T. D. Paine and A. A. Rachford, Dyes Pigm., 2017, 141, 83–92.
15. D.-G. Chen, R. Ranganathan, J.-A. Lin, C.-Y. Huang, M.-L. Ho, Y. Chi and P.-T. Chou, J. Phys. Chem. C, 2019, 123, 4022–4028.
16. C. B. Fialho, T. F. C. Cruz, A. I. Rodrigues, M. José Calhorda, L. F. V. Ferreira, P. Pander, F. B. Dias, J. Morgado, A. L. Maçanita and P. T. Gomes, Dalton Trans., 2023, 52, 4933–4953.
17. C. B. Fialho, T. F. C. Cruz, M. J. Calhorda, L. F. Vieira Ferreira, P. Pander, F. B. Dias, A. L. Maçanita and P. T. Gomes, Dyes Pigm., 2024, 228, 112174.
18. J. Adamek, P. H. Marek-Urban, K. Woźniak, K. Durka and S. Luliński, Chem. Sci., 2023, 14, 12133–12142.
19. S. S. Kothavale and J. Y. Lee, Adv. Opt. Mater., 2020, 8, 2000922.
20. H. Wang, C. Cheng, D. Wang, W. Lou, Y. Zhu, C. Deng, G. Li and Q. Zhang, Org. Electron., 2021, 96, 106254.
21. G. Li, W. Lou, D. Wang, C. Deng and Q. Zhang, ACS Appl. Mater. Interfaces, 2019, 11, 32209–32217.
22. D. Zhou, D. Liu, X. Gong, H. Ma, G. Qian, S. Gong, G. Xie, W. Zhu and Y. Wang, ACS Appl. Mater. Interfaces, 2019, 11, 24339–24348.
23. Y. Yang, L. Yuan, J. Guo, K. Ye, Y. Liu and C. Dou, Dyes Pigm., 2022, 207, 110694.
24. H. Zhang, P.-Z. Chen, L.-Y. Niu and Q.-Z. Yang, Mater. Chem. Front., 2020, 4, 285–291.
25. P. Li, H. Chan, S.-L. Lai, M. Ng, M.-Y. Chan and V. W.-W. Yam, Angew. Chem., Int. Ed., 2019, 58, 9088–9094.
26. L. Zhou, F. Ni, N. Li, K. Wang, G. Xie and C. Yang, Angew. Chem., Int. Ed., 2022, 134, e202203844.
27. Y.-J. Shiu, Y.-T. Chen, W.-K. Lee, C.-C. Wu, T.-C. Lin, S.-H. Liu, P.-T. Chou, C.-W. Lu, I.-C. Cheng, Y.-J. Lien and Y. Chi, J. Mater. Chem. C, 2017, 5, 1452–1462.
28. M. Stanoppi and A. Lorbach, Dalton Trans., 2018, 47, 10394–10398.
29. Y.-J. Shiu, Y.-C. Cheng, W.-L. Tsai, C.-C. Wu, C.-T. Chao, C.-W. Lu, Y. Chi, Y.-T. Chen, S.-H. Liu and P.-T. Chou, Angew. Chem., Int. Ed., 2016, 55, 3017–3021.
30. T. Huang, Z. Chen, Y. Zou, S. Gong and C. Yang, Dyes Pigm., 2021, 188, 109192.
31. M. Urban, P. H. Marek-Urban, K. Durka, S. Luliński, P. Pander and A. P. Monkman, Angew. Chem., Int. Ed., 2023, 62, e202217530.
32. C. Würth, M. Grabolle, J. Pauli, M. Spieles and U. Resch-Genger, Nat. Protoc., 2013, 8, 1535–1550.
33. U. Resch-Genger and K. Rurack, Pure Appl. Chem., 2013, 85, 2005–2013.
34. C. Rothe, S. M. King and A. P. Monkman, Phys. Rev. Lett., 2006, 97, 076602.
35. P. Pander, P. Data and F. B. Dias, JoVE, 2018, e56614.
36. CrysAlis Pro, v. 1.171.38.46, Rigaku Oxford Diffraction, 2018.
37. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122.
38. G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8.
39. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. C.01, Gaussian Inc., Wallingford CT, 2016.
40. A. D. Becke, J. Chem. Phys., 1992, 96, 2155–2160.
41. C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
42. S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211.
43. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627.
44. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
45. R. D. Dennington, T. A. Keith and J. M. Millam, GaussView 6.016, Gaussian Inc., Wallingford CT, 2016.
46. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
47. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
48. R. L. Martin, J. Chem. Phys., 2003, 118, 4775–4777.
49. M. D. Hanwell, D. E. Curtis, D. C. Lonie, T. Vandermeersch, E. Zurek and G. R. Hutchison, J. Cheminf., 2012, 4, 17.
50. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
51. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
52. D. de, S. Pereira, A. P. Monkman and P. Data, JoVE, 2018, e56593.
53. J. Sun, J. Sun, W. Mi, P. Xue, J. Zhao, L. Zhai and R. Lu, Dyes Pigm., 2017, 136, 633–640.
54. P. R. Brooks, M. C. Wirtz, M. G. Vetelino, D. M. Rescek, G. F. Woodworth, B. P. Morgan and J. W. Coe, J. Org. Chem., 1999, 64, 9719–9721.
55. M. Urban, K. Durka, P. Górka, G. Wiosna-Sałyga, K. Nawara, P. Jankowski and S. Luliński, Dalton Trans., 2019, 48, 8642–8663.
56. T. Friščić, C. Mottillo and H. M. Titi, Angew. Chem., Int. Ed., 2020, 132, 1030–1041.
57. P. H. Marek-Urban, D. R. Natkowski, K. Wrochna, A. Zuba, G. Jedrzejczyk, A. Blacha-Grzechnik, M. Grzywa, K. Wozniak and K. Durka, Dyes Pigm., 2024, 231, 112368.
58. D. Frath, J. Massue, G. Ulrich and R. Ziessel, Angew. Chem., Int. Ed., 2014, 53, 2290–2310.
59. Y.-L. Rao and S. Wang, Inorg. Chem., 2011, 50, 12263–12274.
60. P. Pander, A. Swist, R. Motyka, J. Soloducho, F. B. Dias and P. Data, J. Mater. Chem. C, 2018, 6, 5434–5443.
61. S. J. Strickler and R. A. Berg, J. Chem. Phys., 1962, 37, 814–822.
62. S. M. King, M. Cass, M. Pintani, C. Coward, F. B. Dias, A. P. Monkman and M. Roberts, J. Appl. Phys., 2011, 109, 074502.
63. P. Pander, A. V. Zaytsev, A. Sil, J. A. Gareth Williams, P.-H. Lanoe, V. N. Kozhevnikov and F. B. Dias, J. Mater. Chem. C, 2021, 9, 10276–10287.
64. T. J. Penfold, J. Phys. Chem. C, 2015, 119, 13535–13544.
65. C. Wang, W. Chi, Q. Qiao, D. Tan, Z. Xu and X. Liu, Chem. Soc. Rev., 2021, 50, 12656–12678.
66. S. Sasaki, G. P. C. Drummen and G. Konishi, J. Mater. Chem. C, 2016, 4, 2731–2743.

---

Footnote

† Electronic supplementary information (ESI) available: Synthetic procedures, ¹H and ¹³C spectra, HRMS, UV-vis spectra and time-resolved emission spectra; cyclic voltammetry plots, DSC plots, details on X-ray crystallography, additional information on optical properties and theoretical calculations. CCDC 2352195 (7d), 2352196 (8a), 2352197 (8b) and 2352198 (8d). For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4tc03450c

---