Graphene-based polymer composites in thermal management: materials, structures and applications
Luqi
Liu
ab,
Chenchen
Xu
a,
Yuequan
Yang
a,
Chao
Fu
a,
Fuliang
Ma
a,
Zhixiang
Zeng
 *a and
Gang
Wang
*a and
Gang
Wang
 *a
*a
aKey Laboratory of Advanced Marine Materials, Ningbo Institute of Materials Technology and Engineering, Chinese Academy of Sciences, Ningbo 315201, P. R. China. E-mail: zengzhx@nimte.ac.cn; wanggang@nimte.ac.cn
bCenter of Materials Science and Optoelectronics Engineering, University of Chinese Academy of Sciences, Beijing 100049, P. R. China
First published on 2nd October 2024
Abstract
Graphene, with its high thermal conductivity (k), excellent mechanical properties, and thermal stability, is an ideal filler for developing advanced high k and heat dissipation materials. However, creating graphene-based polymer nanocomposites (GPNs) with high k remains a significant challenge to meet the demand for efficient heat dissipation. Here, the effects of graphene material and structure on thermal properties are investigated from both microscopic and macroscopic perspectives. Initially, it briefly introduces the influence of graphene structural parameters on its intrinsic k, along with summarizing methods to adjust these parameters. Various techniques for establishing different thermal conductivity pathways at the macroscopic scale (including filler hybridization, 3D networks, horizontal alignment, and vertical alignment) are reviewed, along with their respective advantages and disadvantages. Furthermore, we discuss the applications of GPNs as thermal interface materials (TIMs), phase change materials (PCMs), and smart responsive thermal management materials in the field of thermal management. Finally, the current challenges and future perspectives of GPN research are discussed. This review offers researchers a comprehensive overview of recent advancements in GPNs for thermal management and guidance for developing the next generation of thermally conductive polymer composites.
Wider impactGraphene is considered the ideal thermally conductive filler for addressing heat accumulation in polymeric materials, owing to its high theoretical k. However, inefficient and low-quality graphene preparation, along with challenges in dispersion, significantly hinder the progress of GPNs in thermal management. Consequently, recent efforts have focused on producing high-quality graphene in various shapes and sizes, as well as creating graphene pathways with different alignments to achieve GPNs with superior k and mechanical properties. A deep understanding of thermal conductivity mechanisms, preparation techniques, and the design of macroscopic thermally conductive structures is crucial for obtaining optimal graphene and GPNs. This review comprehensively investigates the impact of graphene material and structure on thermal properties from both microscopic and macroscopic viewpoints, comparing the pros and cons of different methods for creating thermally conductive pathways in detail. Furthermore, it highlights cutting-edge applications of GPNs in thermal management, while also addressing current research challenges and opportunities. The insights presented in this review aim to equip researchers with a thorough understanding of recent advancements in GPNs for thermal management and offer insights for the development of the next generation of thermally conductive polymer composites. |
1. Introduction
The progressively high heat flow density of electronic devices poses a great challenge to current thermal dissipation technologies.1–3 The 10 °C rule suggests that a 10 °C increase in the operating temperature of a single electronic device results in a 50% reduction in reliability.4 Therefore, there is an urgent need for efficient thermal management materials to address these issues. Polymer materials (both thermoset and thermoplastic, such as epoxy (EP), polystyrene, polycarbonate, polyurethane (PU), polyimide (PI), polyethylene, nylon, etc.) are widely used for thermal management because of their flexibility, insulating properties, processability, and light weight.5 However, their low k (approximately 0.1–0.5 W m−1 K−1) severely limits the rapid development of polymeric materials for thermal management.6,7Graphene is a 2D material with outstanding physical and chemical properties, including high k (∼5000 W m−1 K−1), high surface area (∼2600 m2 g−1), excellent mechanical properties (mechanical strength of 130 GPa), and thermal stability.8–10 It has promising applications in aerospace,11,12 energy harvesting systems,13 energy storage devices,14 and wearable electronics.15 In the past decade, graphene and its derivatives have been proven to be very effective in enhancing the k of various polymers by many researchers.16–18 However, due to its large specific surface area and strong π–π interactions, graphene tends to aggregate and stack together in a way that is difficult to disperse effectively, limiting its use in polymeric materials.19–22 Structural design of graphene is considered a feasible strategy to fully utilize the advantages of graphene and overcome its disadvantage of difficult dispersion.23,24 In addition, the presence of numerous interfaces in GPNs with nanoscale dimensions results in complex heat transfer phenomena. Consequently, a significant number of studies have focused on elucidating the heat transfer mechanisms of graphene nanofillers in polymers and exploring strategies to enhance the k of GPNs.16,25 Meanwhile, increasing k of GPNs while maintaining other advantageous characteristics is a major challenge at present.26
While previous studies have summarized the factors influencing the k and the thermal conductivity mechanism in GPNs, few articles have analyzed the effect of different states of graphene in the polymer matrix on the thermal properties of the composites from the microscopic to macroscopic viewpoints. The different states of graphene at different scales lead to significant differences in the thermal properties of the materials. This work centers around this graphene-induced variability in material properties. First, the influence of structural parameters of graphene (defects, size, number of layers, etc.) on the microscopic intrinsic k of graphene is analyzed, and the current common methods and strategies to modulate these parameters, such as exfoliation of graphene preparation and defect engineering, are summarized. Different surface modifications of graphene are also proposed to address the issue of high interfacial thermal resistance, which arises from poor dispersion and weak contact between graphene and polymer. Subsequently, the effects of different macroscopic polymers formed by graphene with different pathway structures (mainly including hybridized structures of graphene with other materials, 3D graphene networks, and graphene horizontally aligned and vertically aligned) on the thermal properties of the materials are analyzed. Finally, the value of GPNs as TIM, phase change cooling materials, and smart responsive materials for engineering thermal management applications is emphasized, respectively. It is hoped that this work will help researchers gain a deeper understanding of the heat transfer mechanism of GPNs, the laws affecting the thermal properties, and the cutting-edge applications in thermal management, and provide assistance in the subsequent research on GPNs.
2. Peculiarity of graphene material
2.1 Heat transfer mechanism of graphene
The main modes of heat transfer in solids include electronic and phonon conduction. The vibration of the lattice structure plays a decisive role in the heat transfer process for electrically insulating solid materials.27 The process by which an atom undergoes thermal vibrations to transfer energy to neighboring atoms is illustrated in Fig. 1(a). The quantized lattice vibrational energy is called a phonon and can be understood as similar to a photon. The Debye equation shows that the k of a polymer material is proportional to the volumetric heat capacity of materials, the velocity of the phonon group, and the mean free path of the phonons.28 To enhance the k of a material, one can start by enhancing the velocity and the mean free path of the phonon group. Graphene is a 2D material composed of sp2 hybridized carbon atoms with extremely high specific surface area and a unique six-membered carbocyclic conjugated large π-bonding structure (Fig. 1(b)).29 The k of graphene is mainly contributed by phonons, transferring energy in a ballistic-diffusive manner.30 The k of free monolayer graphene has an ultra-high k of 5.0 × 103 W m−1 K−1 at room temperature, which is much higher than that of other common materials (Table 1). The fundamental reason for the extremely high k of graphene is that it has a 2D honeycomb lattice structure, which facilitates a significant reduction of phonon scattering at grain boundaries and has a phonon mean free path of up to 775 nm.31 Moreover, due to the lightness of the carbon atoms, monolayer graphene connected by covalent bonds has an extremely high speed of sound. However, the k of graphene is anisotropic, and it has a low axial k because the layers of graphene act through weak van der Waals forces.32,33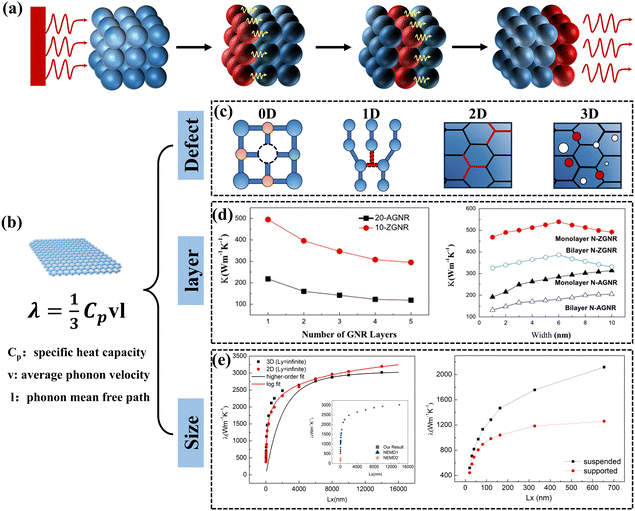 | ||
| Fig. 1 (a) Schematic diagram of the process by which atoms transfer energy to neighboring atoms through thermal vibrations. (b) Schematic diagram of graphene's special structure. (c) Four defects that affect graphene k. (d) Layer and size dependence of k in multilayer graphene nanoribbons (Copyright©2011 Elsevier B.V. All rights reserved).34 (e) Size effect of k in monolayer graphene (Copyright©2018 Elsevier Ltd. All rights reserved).35 | ||
| Categorization | Material | k (W m−1 K−1) | Density (g cm−3) |
|---|---|---|---|
| Metal | Ag | 428 | 10.4 |
| Cu | 398 | 8.9 | |
| Au | 315 | 19.3 | |
| Al | 247 | 2.7 | |
| Mg | 151 | 1.7 | |
| Fe | 94 | 7.9 | |
| Ni | 88 | 8.9 | |
| Carbon | Graphene | 5000 | 2.3 |
| Graphite | 200–2000 (‖) | 2.1 | |
| 2–800 (⊥) | |||
| SWCNTs | 6000 | — | |
| MWCNTs | 3000 | — | |
| PAN-based CF | 8–105 | 1.8 | |
| Pitch-based CF | 1100 | 2.2 | |
| Diamond | 600–2000 | 3.5 | |
| Ceramics | BeO | 250–300 | 3.0 |
| MgO | 36 | 3.6 | |
| Al2O3 | 30 | 3.5 | |
| AlN | 170–220 | 3.3 | |
| SiC | 150 | 3.2 | |
| BN (cubic) | 1300 | 5.2 | |
| BN (hexagonal) | 600 (‖) | 2.1 | |
| 30 (⊥) |
The k of graphene can be affected by many factors, including defects,36,37 number of atomic layers,34 and size.38 Various defects such as point defects (vacancies and interstitial atoms), line defects (dislocations), surface defects (grain boundaries and phase interfaces), and bulk defects (cavities and bubbles) are unavoidably present in every crystal (Fig. 1(c)).39,40 For single-layer graphene, often exhibits point defects and line defects, primarily comprising single-vacancy (SV), Stone–Wales (SW), double-vacancy (DV), and multi-vacancy (MV). Studies of molecular dynamics and non-equilibrium Green's function-based simulation methods have shown that defects tend to reduce the k of graphene, which is attributed to the fact that the defects lead to scattering of phonons, reducing the mean free path of the phonons.41–44Fig. 1(d) shows that the k of graphene is related to the number of atomic layers, which tends to decrease at room temperature as the number of atomic layers increases.34 This is due to the different frequencies of phonon vibrations between the different atomic layers, and the inconsistency of the normal modes (different frequencies) of these vibrations creates a “thermal resistance”.27 The size of graphene is also an influential factor in k. When the length of graphene is much larger than the phonon means free path, the k continues to increase with the graphene length up to a constant value (Fig. 1(e)).35 Wang et al. summarized similar conclusions and showed that this result was related to the change in the mode of transport of phonons in graphene.45 Large-size, defect-free, monolayer graphene is an ideal thermally conductive filler. However, when graphene is introduced into the polymer matrix, the amorphous polymer chains can severely hinder the heat transfer process of graphene, resulting in the k of GPNs being much lower than the ideal value. This reveals the complex heat transfer mechanism of GPNs triggers continuous exploration by scholars.
2.2 Heat transfer mechanism of GPNs
With the development of electronic products, GPNs have received much attention as thermally conductive materials.46–48 GPN consists of a polymer matrix and thermally conductive fillers (Fig. 2(a)). The polymer matrix exhibits a low k due to defects within the polymer chains. Additionally, the intricate spatial structure resulting from the entanglement of these chains can cause significant phonon scattering (Fig. 2(b)).49 Introducing high k graphene into polymeric thermally conductive materials is considered to be promising. However, the k values of polymer composites filled with fillers are much lower than theoretical expectations.50 Despite high loading, the k never reaches the intrinsic value of the filler. This is mainly due to the presence of an interfacial thermal resistance (also known as Kapitza thermal resistance) between the polymer matrix and the filler, which impedes the transfer of heat flux (Fig. 2(c)).51 This interfacial thermal resistance is caused by the phonon vibration mismatch between the polymer matrix and the filler as well as between the filler and the filler.52,53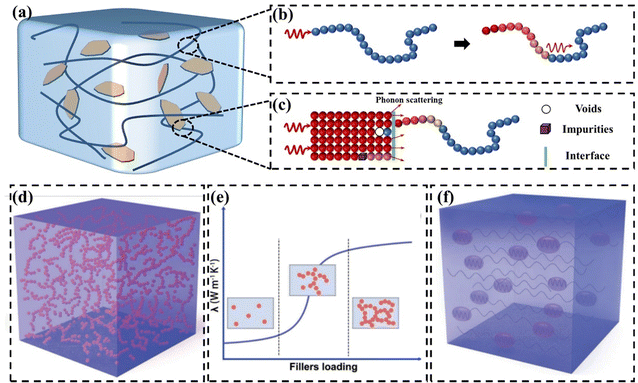 | ||
| Fig. 2 (a) Representation of a nanocomposite loaded with fillers. (b) Severe phonon scattering is caused by the complex spatial structure formed by the entanglement of polymer chains. (c) Kapitza thermal resistance (d) thermal conduction paths at high filler content (Copyright©2023 Wiley-VCH GmbH).21 (e) Thermal percolation theory.21 (f) Thermoelastic coefficient theory.21 | ||
The main mechanisms of heat conduction in GPNs recognized so far are the thermal conduction path theory,54–56 the thermal percolation theory,57,58 and the thermoelastic coefficient theory.21,59 The thermal conduction path theory is the most widely accepted thermal conduction mechanism. When the loading is low, the fillers are isolated and dispersed from each other. Gradually increasing the concentration of fillers, they contact each other in the polymer matrix to form a pathway, which facilitates rapid heat flux transfer (Fig. 2(d)). Thermal penetration theory suggests that there is a process of abrupt change in the k of polymer composites as the filler content reaches the penetration threshold (Fig. 2(e)).60 Comparing the polymer matrix to an ocean, the filler is like an island. When the loading of the filler is low, the filler forms a “sea-island” system in the polymer matrix, and they are isolated from each other. As a result, there is no significant improvement in the k values of the polymer composites. After the loading of the filler reaches the penetration threshold, the k values of the polymer composites rapidly increase. Nevertheless, some polymer composites do not show significant “heat penetration”.61 This is difficult to explain by the theory of heat penetration, which is still controversial. Based on the similarity between the vibration law of phonon and the change law of elasticity coefficient in classical vibrational mechanics, some researchers regarded the k as the thermal elasticity coefficient in the propagation process of phonon and proposed the theory of thermal elasticity coefficient (Fig. 2(f)).62 The k depends on the macroscopic properties of the whole material, and the increase in k of polymer composites can be regarded as the enhancement of the polymer matrix by high fillers.59 The value of the k of the composites gradually increases with the increase in filler content. Polymer matrix and filler are two phases with different thermoelastic coefficients. In the same way that vibrations and waves are reflected, refracted, and interfered at the interface of two phases with different coefficients of elasticity, phonons are also scattered, hindering thermal conduction.
Theoretically, large-sized, defect-free, monolayer graphene is an ideal thermally conductive filler for filling in polymers. However, in polymer composites, the configuration of the filler has a different effect on the k of the composite due to the interfacial thermal resistance. When the filler loading is low, multilayers of graphene are more favorable to enhance the k. Shen et al.63 demonstrated through multiscale modeling and experimental methods that multilayer graphene nanosheets with identical aspect ratios consistently enhance the k of composites more effectively than single-layer nanosheets. This finding is further corroborated by Li et al. using molecular dynamics methods.9 Therefore, substituting multilayer graphene sheets for monolayer sheets represents a more effective strategy for improving the k of composites.64,65 However, phonon scattering caused by surface defects is usually the main provider of the total thermal resistance of composites. The interfacial thermal resistance between the polymer and the filler is the key factor affecting its k.66 Overall, defect-free and large aspect ratio graphene contributes to the enhancement of the k of polymer composites, which poses high requirements and challenges for the preparation process of graphene nanosheets.
2.3 Modulation of the number of layers and size of graphene
Since the size and number of layers of graphene have a great influence on its thermal properties, the thickness and size of graphene need to be precisely regulated. Common regulation methods include mechanical exfoliation,67 epitaxial growth,68 chemical vapor deposition (CVD),69 and chemical exfoliation.70 Mechanical exfoliation is the original method of exfoliating graphite, which is mainly used to overcome the interaction between graphite layers by ultrasound or shear, etc. SiC epitaxial growth, a method of preparing single-crystal graphene on a single-crystal substrate, is also considered to be an effective means of producing large-area, high-quality graphene. However, the disadvantages of above two methods are low exfoliation efficiency and uncontrollable thickness and size. CVD is a technique that produces large-area and high-quality continuous graphene films on metal surfaces at high temperatures, allowing for fine control of the number of layers and the size of graphene. Nevertheless, this method is time-consuming and costly and is not conducive to high-volume preparation. In contrast, chemical exfoliation is a promising and effective method for low-cost macro-preparation of graphene. However, most of the prepared graphene is a mixture of monolayer, bilayer and multilayer graphene. All of the above methods used to regulate the number of layers and the size of graphene have their own advantages and disadvantages, and need to be selected according to the actual conditions and demands.2.4 Defect modulation of graphene
Heat conduction in graphene is often greatly hindered by defects, which has driven many scholars to research defect repair. Graphene oxide (GO), with its high yield and ease of preparation, is often used as an alternative to graphene. However, to realize the thermal properties of graphene, it is necessary to repair the functional group defects on GO. The common methods for removing oxygen-containing functional groups from GO are chemical reduction and high-temperature annealing. Chemical reduction is carried out by adding reducing agents such as hydrazine hydrate, alcohols, and sodium borohydride.71 Zhang et al. successfully synthesized reduced graphene oxide (rGO) by reducing GO using hydrazine hydrate (Fig. 3(a)).72 Xue et al. demonstrated that reducing GO with hydrazine hydrate produces rGO with a high carbon-to-oxygen (C/O) ratio. The rGO/polypropylene nanocomposites exhibited significant improvements in tensile strength, thermal conductivity, and thermal stability as the C/O ratio of rGO increased, achieving enhancements of 20.5% in tensile strength and 54.5% in thermal conductivity compared to pure polypropylene.73 The chemical reduction of GO eliminates various oxygen-containing groups while forming C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bonds and partially restoring the conjugated structure of graphene. However, this method faces challenges in completely removing oxygen-containing groups and excess reductants, making high-temperature annealing a practical alternative. Song et al. effectively increased the thermal conductivity of GO films to 1043.5 W m−1 K−1 through annealing. Higher temperatures (greater than 500 °C) facilitate the removal of functional groups and enhance the conversion of sp3 to sp2 carbon in the graphite lattice (Fig. 3(b)).74 Nevertheless, these methods cannot perfectly enhance the structural integrity of graphene and new defects may be introduced during the reduction process.75 Therefore further enhancement of graphene properties requires repair of lattice defects.
C double bonds and partially restoring the conjugated structure of graphene. However, this method faces challenges in completely removing oxygen-containing groups and excess reductants, making high-temperature annealing a practical alternative. Song et al. effectively increased the thermal conductivity of GO films to 1043.5 W m−1 K−1 through annealing. Higher temperatures (greater than 500 °C) facilitate the removal of functional groups and enhance the conversion of sp3 to sp2 carbon in the graphite lattice (Fig. 3(b)).74 Nevertheless, these methods cannot perfectly enhance the structural integrity of graphene and new defects may be introduced during the reduction process.75 Therefore further enhancement of graphene properties requires repair of lattice defects.
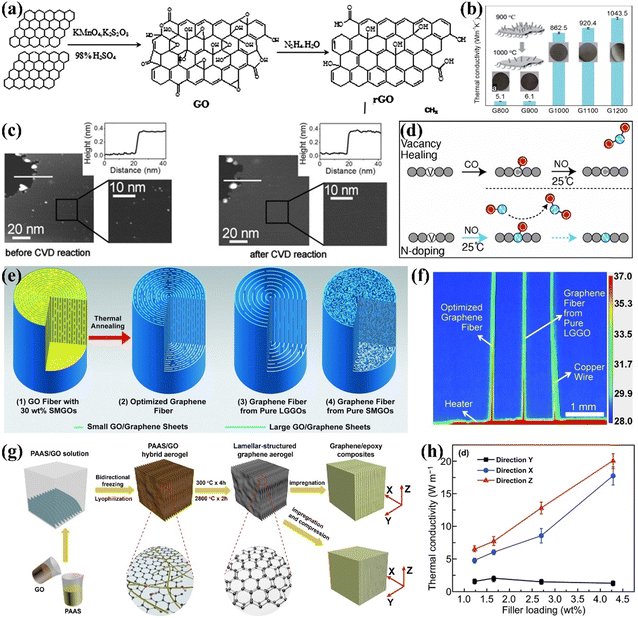 | ||
| Fig. 3 (a) The process of reducing GO with hydrazine hydrate (Copyright©2016 Elsevier Ltd. All rights reserved).72 (b) In-plane k of rGO films at different annealing temperatures.74 (c) Repair of single-layer depth defects in highly oriented pyrolitic graphite surfaces by CVD processing (Copyright©2011 Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim).76 (d) Schematic illustration of the healing and N-doping of graphene vacancies using CO and NO molecules.77 (e) Schematics of the “intercalated” structure of the GO fibers and graphene fibers, and (f) thermal imaging of fast heat transfer on graphene fibers.78 (g) Schematic of the fabrication of layered structured graphene aerogels and their EP composites, and (h) plots of the k of the composites as a function of graphene content in three orientations (Copyright©2020, The Author(s)).79 | ||
The main repair methods for lattice defects in GO include CVD, doping, liquid phase repair, external energy graphitization, and alloying repair. Essentially, lattice defects present in GO can be restored by filling with C radicals or hetero atoms from a C source.80 For example, Kholmanov et al. treated highly oriented pyrolytic graphite using CVD with an acetylene carbon source. Acetylene gas decomposes to supply C atoms for repairing defects. Scanning tunneling microscopy tests revealed that the single-layer depth defects in CVD-treated graphene were repaired, resulting in a perfect honeycomb structure (Fig. 3(c)). But the CVD method makes it difficult to repair multilayer defects.76 Wang et al. demonstrated through first-principles molecular dynamics simulations that vacancies exposed to CO and NO molecules could be healed. CO molecules are trapped in the vacancies, while excess O radicals are removed by NO to form NO2. This CO–NO combination effectively facilitates both repair and doping without introducing additional defects (Fig. 3(d)).77 However, the challenging repair of the polymer matrix and the low efficiency of defect repair restrict the use of graphene as a thermally conductive filler in polymer composites. High-temperature graphitization is a widely used method for repairing lattice defects due to its advantages, which include a straightforward preparation process and high productivity. Xin et al. showed that high-temperature treatment at 2850 °C increased the thermal conductivity of graphene flake fibers from 400 W m−1 K−1 to 1300 W m−1 K−1 by eliminating structural defects, as indicated by the disappearance of the D peak in Raman spectra (Fig. 3(e) and (f)).78 Liu et al. combined high-temperature graphitization of graphene aerogel with vacuum impregnation of EP to create composites with a high k of 20.0 W m−1 K−1 at 2.30 vol% graphene content, as elevated temperatures removed residual oxygen-containing groups and repaired structural defects (Fig. 3(g) and (h)).79 Using a similar approach, An et al. achieved an exceptionally high k of 35.5 W m−1 K−1 for graphene-hybridized foam/EP composites with a rGO content of 19.0 vol%.81
2.5 Surface modification of graphene
Improving the intrinsic k of graphene in polymer composites is crucial, but enhancing compatibility between graphene and the polymer matrix is equally important. Increased compatibility reduces phonon vibrational mismatch during heat transfer and improves the dispersion of the filler.82 Graphene surface functionalization, which includes covalent and non-covalent methods, effectively enhances interfacial compatibility. Covalent bonding introduces functional groups (like –OH, –COOH, –C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, and –O) that strengthen interfacial bonding energy, thus improving heat transfer efficiency.83 A study utilizing molecular dynamics simulated the effects of various functionalizations on the interfacial k of graphene–EP composites, concluding that covalent bonds enhance interfacial interactions and phonon transfer.84 However, while creating active sites for these covalent reactions, the introduction of functional groups can lead to lattice defects, significantly reducing k, as discussed in Section 2.4. Non-covalent functionalization, increasingly recognized in recent years, utilizes blending or reacting with materials (like surfactants, polymers, organic molecules, and biomolecules) to bridge the gap between graphene and the polymer matrix. This method promotes compatibility through various interactions (ionic, hydrogen bonding, π–π interactions, van der Waals forces, electrostatic interactions), without compromising graphene's intrinsic thermal conductivity.85 Nevertheless, the introduction of non-covalent functional groups introduces impurities that can impact the k of the composites. Additionally, aligning graphene consistently is challenging due to its dissociative nature. Researchers still have significant opportunities to improve the k of polymer composites by modulating the interfaces of graphene.
O, and –O) that strengthen interfacial bonding energy, thus improving heat transfer efficiency.83 A study utilizing molecular dynamics simulated the effects of various functionalizations on the interfacial k of graphene–EP composites, concluding that covalent bonds enhance interfacial interactions and phonon transfer.84 However, while creating active sites for these covalent reactions, the introduction of functional groups can lead to lattice defects, significantly reducing k, as discussed in Section 2.4. Non-covalent functionalization, increasingly recognized in recent years, utilizes blending or reacting with materials (like surfactants, polymers, organic molecules, and biomolecules) to bridge the gap between graphene and the polymer matrix. This method promotes compatibility through various interactions (ionic, hydrogen bonding, π–π interactions, van der Waals forces, electrostatic interactions), without compromising graphene's intrinsic thermal conductivity.85 Nevertheless, the introduction of non-covalent functional groups introduces impurities that can impact the k of the composites. Additionally, aligning graphene consistently is challenging due to its dissociative nature. Researchers still have significant opportunities to improve the k of polymer composites by modulating the interfaces of graphene.
3. The structures of graphene in GPNs
Thermally conductive fillers are essential for the performance of GPNs. Initially, graphene was incorporated into the polymer matrix using methods such as solution mixing, in situ polymerization, and melt mixing.86 When graphene is dispersed, the surrounding polymer hinders thermal conduction between the fillers. Therefore, it is essential to increase the filler loading until the percolation threshold is reached to enhance thermal performance by improving contact among the graphene particles. However, a high filler load can lead to clustering due to strong π–π interactions, which limits the thermal conductivity of GPNs. Additionally, larger amounts of filler can compromise the flexibility and compressibility of GPNs, hindering their development and application.87 As the heat flow density in chips increases, traditionally prepared GPNs struggle to meet the demanding heat dissipation requirements of electronic components. Consequently, researchers are focusing on achieving high k in GPNs with lower filler loads. Recognized methods to enhance the k of GPNs include improving the inherent k of the fillers, creating effective thermal pathways, and reducing interfacial thermal resistance.16 Since methods to enhance the intrinsic k of graphene and reduce interfacial thermal resistance were presented in the previous section, this section will summarize strategies specifically related to the construction of effective thermal conductivity pathways.3.1 Hybridization of thermally conductive fillers
The key to enhancing k by conventional blending methods lies in improving the dispersion of graphene and lowering the thermal percolation threshold of the material. The incorporation of a single filler is limited in improving the k of polymer composites, mainly owing to the difficulty in uniformly dispersing a single filler and the severe phonon scattering at the interface between the filler and the polymer matrix. The dispersion of fillers in the polymer matrix can be improved by hybridizing multiple fillers into the polymer matrix. The synergistic effect of multiple shapes of fillers helps fillers to construct thermally conductive pathways by bridging and filling the voids, which greatly enhances the heat transfer performance of the composites.88,89 Graphene nanoparticles (GNPs) are often chosen as a hybridized filler because it has a large aspect ratio, few interfaces, and can form a thermally conductive pathway through face contact. Other fillers with high k are also frequently used, including 0D fillers (e.g., silicon carbide, diamond, alumina, copper nanoparticles, etc.), 1D fillers (e.g., carbon nanotubes (CNTs), carbon nanofibers, silver nanowires, and cellulose nanofibers, etc.), and 2D fillers (e.g., boron nitride nanosheets (BNNS), etc.). These hybridized thermally conductive fillers have been reported to exhibit synergistic effects in polymer composites.90,910D fillers require that the size of all three dimensions must be less than 100 nm. When hybridized with 2D graphene nanosheets and incorporated into a polymer matrix, these fillers can effectively fill the voids between the nanosheets. 0D fillers are becoming increasingly prevalent in GPNs because of their ease of production and their ability to enhance the functionality and characterization of the composites. Metal nanoparticles with high k are often employed to improve the k of these composites, primarily relying on electron heat transport and exhibiting an extremely short mean-free path. Barani et al. incorporated a mixture of fillers, including few-layer graphene (with a size of a few micrometers, 40 wt%) and copper nanoparticles (with a size of a few nanometers, 35 wt%), into EP composites. The resulting k increased by 6750%, reaching 13.5 ± 1.6 W m−1 K−1. Copper nanoparticles were positioned between the graphene sheets (Fig. 4(a)), forming a thermally conductive network that combined phonon and electron transport, demonstrating significant potential for TIM.92 However, due to the excellent electrical conductivity of graphene and metal fillers, GPNs can be challenging to use in electronic devices with high insulation requirements. To harness the exceptional thermal conductivity of graphene while achieving satisfactory electrical insulation in the composites, a critical strategy is to inhibit electron transfer between neighboring graphene sheets by coating insulating particles on their surfaces. Shen et al. successfully grew a layer of SiO2 particles on graphene nanosheets using the sol–gel method, resulting in polydimethylsiloxane (PDMS) based composites with excellent thermal conductivity and electrical insulation. This improvement was primarily attributed to the insulating SiO2 coating preventing electron transfer between graphene while enhancing inter-component interactions, ensuring uniform dispersion of graphene, and creating an efficient thermal conductivity pathway (Fig. 4(b)).93 In a study by Lv et al., alumina-coated graphene flakes were utilized to produce EP composites with high k and low electrical conductivity. A dense Al2O3 layer formed a mesh structure on the graphene sheet surface, serving as an insulator. The EP composites achieved a k of 0.97 W m−1 K−1 with 30 wt% mixed filler, while electrical resistivity remained above 1011 Ω cm.94
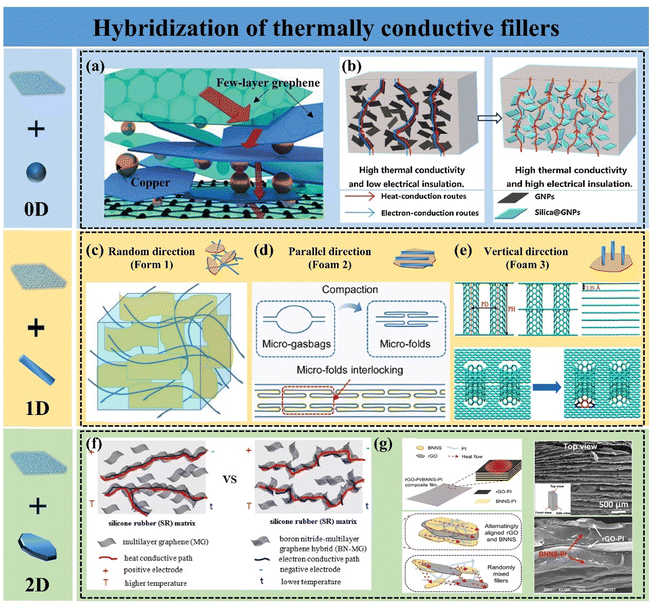 | ||
| Fig. 4 (a) Schematic of the formation of thermal conduction pathways by bridging Cu nanoparticles with GNPs (Copyright©2019 Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim).92 (b) Schematic diagram of the formation of thermal and electrical conduction pathways in silica@GNP/PDMS composites (Copyright©2019, Elsevier).93 Three composite forms of CNTs and graphene, including (c) random distribution (Copyright©2021 Wiley Periodicals LLC),95 (d) horizontal orientation (Copyright©2022 Elsevier Ltd and Techna Group S.r.l. All rights reserved),96 and (e) vertical orientation (Copyright©2023 Elsevier Ltd. All rights reserved).97 (f) Schematic of the thermal and electrical conduction paths of SR/graphene and SR/BN–graphene composites.98 (g) SEM images of the rGO/BNNS/PI composite and a schematic illustrating the mechanism behind its high thermal conductivity (Copyright©2020 Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim).99 | ||
1D filler is a material characterized by dimensions smaller than 100 nm in at least two directions and demonstrates high k in one dimension. CNTs are one of the common 1D thermally conductive fillers with k up to 1000–4000 W m−1 K−1. Hybridization of CNTs and GNPs can synergistically enhance the k of GPNs. To fully leverage the anisotropic properties of 1D fillers, CNTs are aligned differently according to the requirements of GPNs. There are three main composite forms of CNTs and graphene, including random distribution (Form 1), horizontal alignment (Form 2), and vertical alignment (Form 3). For the filler random distribution system, CNTs tend to adsorb on the surface of GNPs to form a cross-network (Fig. 4(c)). Compared to the random distribution of a single filler, the incorporation of CNTs usually reduces the restacking of graphene for dispersion, and the CNTs act as bridges connecting the GNPs, which effectively enhances the heat flux transport and uniform distribution.95 In thin-film GPNs, fillers are often present in a horizontal arrangement. Generally, hybridizing CNTs with graphene enhances the in-plane k of films. Xiong et al. prepared horizontally aligned graphene/CNT films via synthesis and compaction. The AB stacking of CNT and graphene facilitated phonon propagation, resulting in an in-plane k of 1280.3 W m−1 K−1 (Fig. 4(d)).96 However, it is controversial whether the incorporation of CNTs improves the k of graphene films under Form 2. Xing et al.100 employed molecular dynamics simulation methods and experimental analysis to systematically explore the mechanism of CNTs’ influence on the k of graphene films. It was shown that with the addition of CNTs, the in-plane k of the hybridized films decreases while the through-plane k increases, which is mainly due to the increase of defect density by the introduction of CNTs and the creation of covalent bonding between the CNTs and graphene leading to lattice distortion of GNPs, exacerbating the low-frequency phonon scattering. However, the introduction of CNTs provides more channels for phonon transfer in the through-plane direction. Hu et al.101 reported a GO-doped carbon nanotube hybridized film with k up to 1056 W m−1 K−1. The removal of defects within the film by high-temperature annealing and the formation of covalent bonds between the CNTs and graphene sheets resulted in the hybridized film having superior properties compared to those prepared by other methods. To improve the k in the through-plane direction, Georgios K. et al.102 in 2008 reported for the first time a columnar graphene structure consisting of a 1D CNT and a 2D graphene, which corresponds to Form 3. This 3D structure consists of variable-distance parallel graphene layers connected by CNTs placed perpendicularly to the graphene planes. Lin et al.97 demonstrated, using inverse nonequilibrium analytical kinetics (Fig. 4(e)), that carbon nanotube incorporation enhanced the heat transfer between graphene planes but also led to lattice distortion of graphene. Nevertheless, by strategically designing the quantity of CNTs and the number of layers of columnar graphene, the interfacial thermal conductivity between graphene and EP can be significantly enhanced. Regardless of the filler arrangement, the incorporation of CNTs can enhance heat transfer by efficiently constructing the thermal conduction pathways, but the introduction of crystal defects should be avoided.
Compared to 0D and 1D fillers, 2D fillers can partially substitute for graphene due to their high aspect ratio and similar crystal structure. Hexagonal boron nitride, commonly known as BN, is extensively utilized in the thermal management of electronic devices because of its high thermal conductivity (∼600 W m−1 K−1), exceptional mechanical properties, favorable thermal stability, and outstanding electrical insulation.103 The hybridization of boron nitride with graphene not only enhances the thermal transfer performance of GPNs but also imparts new properties to them. According to Deng,98 the electrostatic self-assembly method was employed to hybridize graphene with BNNSs, resulting in a silicone rubber (SR)/BNNS–graphene composite that exhibits excellent insulating properties while maintaining high k (Fig. 4(f)). Feng et al. demonstrated that the GPNs produced through the hybridization of BNNSs with graphene also exhibit synergistic effects in flame retardancy.104 In addition to the inherent properties of BNNSs, a well-considered structural design can further enhance the performance of GPNs. Guo et al. combined conductive rGO with insulating BN to create PI composites with a high dielectric constant, low dielectric loss, high energy density, and exceptional k. The micro-sandwich structure facilitates continuous thermal conductivity pathways for both graphene and BNNSs (Fig. 4(g)), which synergistically improves the k of the hybrid filler without compromising its electrical properties. Ultimately, this approach allows for the achievement of performance requirements at significantly lower filler loadings compared to those reported in most studies.99
In conclusion, the hybridization of fillers with varying shapes and graphene nanosheets can result in GPNs that possess distinct characteristics. This approach allows GPNs to generally exhibit several advantages, including enhanced performance, diversified functionality, improved dispersion, reduced costs, and optimized interfacial interactions, all of which contribute to their increased utility. However, several challenges remain that require further investigation. For instance, certain types of fillers, such as BNNSs and CNTs, are currently difficult to produce in high quality and large quantities.105 Additionally, GPNs created through simple hybridization methods may not meet the current demands of high heat flow density electronic devices. This limitation arises because simple hybridization does not adequately control the contact configuration between fillers, leading to significant interfacial thermal resistance. Therefore, to minimize microscopic interfacial thermal resistance, it is essential not only to select fillers with complementary properties but also to regulate the bonding state at the filler interface.
3.2 3D network alignment of graphene
Simple blending of fillers in polymers can effectively enhance the k of the material through synergistic effects, but sometimes the enhancement of k can be affected by the increase of thermal resistance due to the increase of contact area.106 How to further enhance the k of polymer composites by reducing the interfacial thermal resistance remains an open question.107 The combined design of distribution, orientation, and continuity is crucial to achieve the desired thermal properties of the material.108 The synthesis of continuously oriented graphene structures in polymer matrices is an effective strategy for the development of high-performance polymer composites.109 Xie et al. proposed that the continuity design determined the magnitude of the thermal interactions between reinforcement and matrix, and the control of orientation is a key process to achieve a selective thermal response.108 Therefore, the construction of thermally conductive pathways can modulate the macroscopic properties of the GPNs. In recent years, there has been an increasing interest in constructing 3D interconnected structures as thermally conductive networks, which ensure good dispersion of low-loaded fillers while minimizing the detrimental effects of interfacial thermal resistance at the filler-filler interface.22 For example, Li et al.110 constructed a 3D thermal conductivity network of copper and graphene composite, which improved the k of EP by a factor of 11 owing to the reduction of the filler-filler interfacial thermal resistance. Zhang et al.22 summarized a large number of studies on the preparation methods of dispersed fillers and 3D interconnection networks, and found that composites with 3D interconnection networks were more likely to obtain high k at relatively low filler fractions. At present, there has been in-depth research on the technologies to construct 3D graphene interconnection networks, mainly including template method, self-assembly method, 3D printing technology and so on.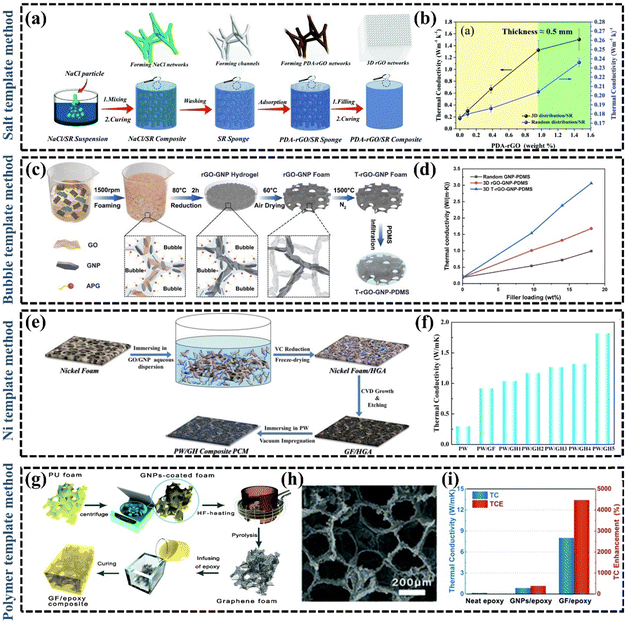 | ||
| Fig. 5 (a) Schematic illustration of the preparation process of the PDA–rGO/SR composite with 3D interconnected graphene networks (Copyright©2021 Elsevier B.V. All rights reserved).111 (b) The TCs of PDA–rGO/SR composites.111 (c) Schematic illustration of the fabrication procedure of 3D rGO–GNP–PDMS composites (Copyright©2021 Elsevier B.V. All rights reserved).112 (d) Effect of the GNP content on the k values of random GNP-PDMS, 3D rGO–GNP–PDMS, and 3D T-rGO–GNP–PDMS composites.112 (e) Schematic illustration of the preparation of GO/GNP/PW composites (Copyright©2017 Published by Elsevier B.V.).118 (f) The k of pure PW, and PW composites.118 (g) Preparation process of graphene foam/EP composites.120 (h) SEM image of graphene foam.120 (i) The k of graphene foam/EP composites.120 | ||
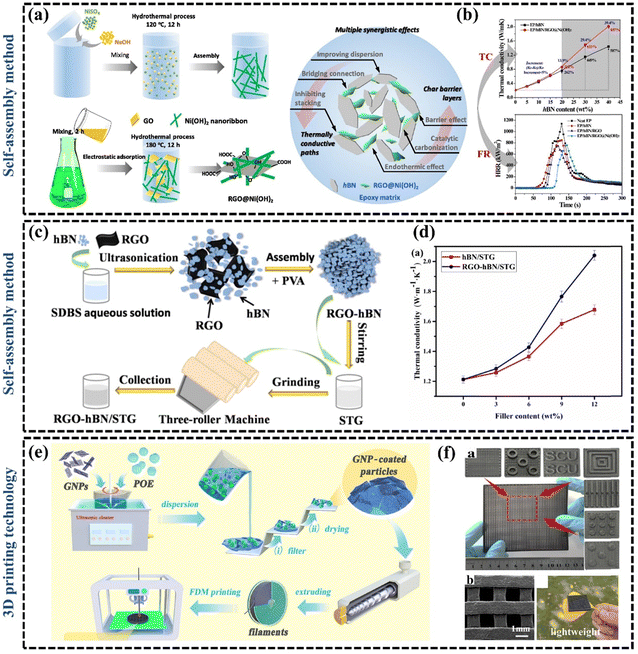 | ||
| Fig. 6 (a) Illustrations of synthesis routes of rGO@Ni(OH)2 hybrid by “two-step” hydrothermal process and multiple synergistic effects of BN and rGO@Ni(OH)2 hybrid in EP matrix (Copyright©2019 Elsevier B.V. All rights reserved).104 (b) The k of EP/BN and EP/BN/rGO@Ni(OH)2 composites as a function of BN content and heat release rate of neat EP and its composites with 20 wt% BN and 2 wt% graphene.104 (c) Scheme for the preparation of rGO–BN/silicone thermal grease (Copyright©2022, American Chemical Society).48 (d) The k of BN/silicone thermal grease and rGO–BN/silicone thermal grease with different filler contents.48 (e) Schematic diagram for preparation of polyolefin elastomer/GNP filaments and the 3D printing process (Copyright©2022, American Chemical Society).126 (f) SEM images, ultra-depth images, and digital photos of printed flexible polyolefin elastomer/GNP pads.126 | ||
3.3 Horizontal alignment of graphene
Besides the method of 3D interconnecting thermally conductive pathways, aligning thermally conductive fillers can enhance heat transfer in specific orientations. The perfect orientation of 2D graphene can maximize its excellent in-plane properties and lower the percolation threshold of the material. A crucial strategy for creating highly anisotropic thermally conductive nanocomposites involves aligning the fillers along the in-plane direction within the polymer matrix. This enables the establishment of horizontal thermal conductivity pathways, thereby maximizing the in-plane k.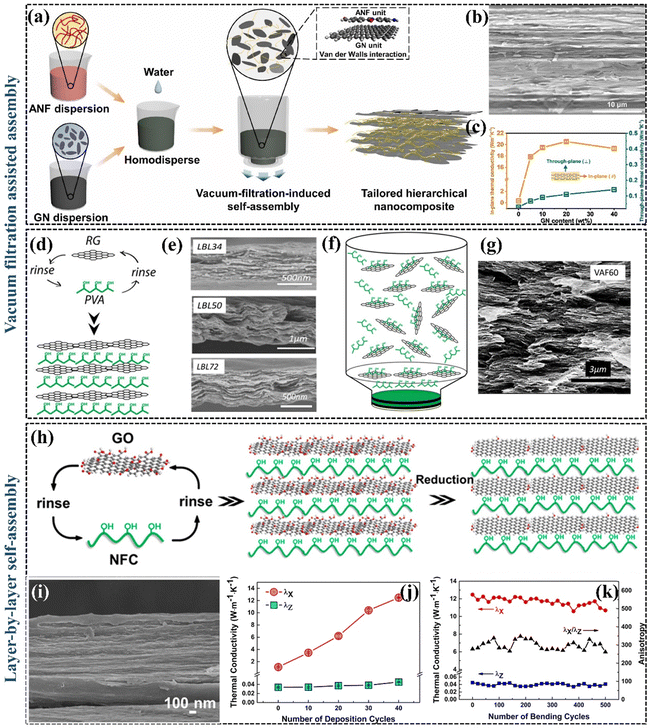 | ||
| Fig. 7 (a) Schematic illustration of the preparation process of aramid nanofibers/GNP nanocomposites (Copyright©2022 Elsevier Ltd. All rights reserved).132 (b) SEM image of aramid nanofibers/20% GNP nanocomposite film.132 (c) In-plane and out-plane k of aramid nanofibers nanocomposite films prepared with different GNP contents.132 (d) A schematic drawing of LBL assembly (Copyright©2013, American Chemical Society).133 (e) SEM images for the cross-sectional areas of LBL34, LBL50, and LBL72. (f) A schematic drawing of vacuum filtration-assisted assembly.133 (g) SEM image for the cross-sectional areas of vacuum filtration-assisted 60.133 (h) Schematic drawing of the preparation of the hybrid films (Copyright©2017, American Chemical Society).135 (i) The cross-section of the thermally conductive coating layer.135 (j) kX and kZ of LBL-assembled (nanofibrillated cellulose/rGO)n hybrid film with different numbers of deposited cycles on a nanofibrillated cellulose substrate.135 (k) kX, kZ, and kX/kZ of (nanofibrillated cellulose/rGO)40 hybrid film under different numbers of bending cycles.135 | ||
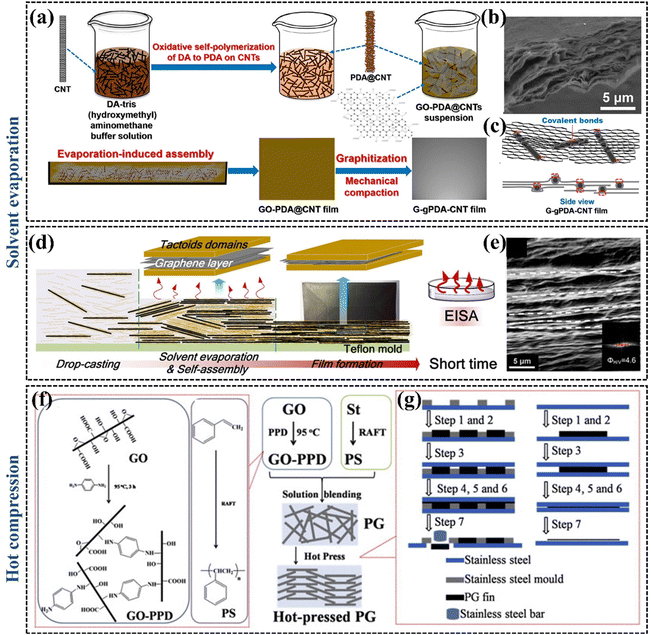 | ||
| Fig. 8 (a) The preparation process of the G–gPDA–CNT films (Copyright©2020, American Chemical Society).137 (b) SEM image showing the microstructure of the cross-section of G–gPDA–CNT-7.5% film (Copyright©2018, American Chemical Society).137 (c) Mechanism of the G–gPDA–CNT-7.5% film (Copyright©2018, American Chemical Society).137 (d) Schematic representation of the vacuum filtration-assisted assembly and solvent evaporation fabrication of rGO/oxidized cellulose nanocrystal nanocomposites (Copyright©2018, American Chemical Society).139 (e) SEM image of rGO/oxidized cellulose nanocrystal nanocomposites.139 (f) and (g) The preparation of hot-pressed PG thermal conductive fins (Copyright©2015 Elsevier Ltd. All rights reserved).140 | ||
3.4 Vertical alignment of graphene
To achieve effective through-plane heat transfer in GPN materials, researchers created vertically aligned 3D graphene structures that leverage graphene's superior in-plane thermal conductivity and various methods to integrate them with polymer matrices. Lin et al.141 prepared four TIM (pristine PDMS/randomly dispersed graphene-based PDMS composites/horizontally oriented graphene backbone PDMS composites/axially oriented graphene backbone PDMS composites) by freeze-drying and vacuum impregnation. By comparing their k, it was found that graphene backbone PDMS composites with vertical orientation had a significant improvement. The reason is that vertically oriented graphene networks can provide shorter transmission paths and enhance the transmission rate, for which a great deal of effort has been made in constructing vertically aligned graphene networks to form fast heat transfer channels.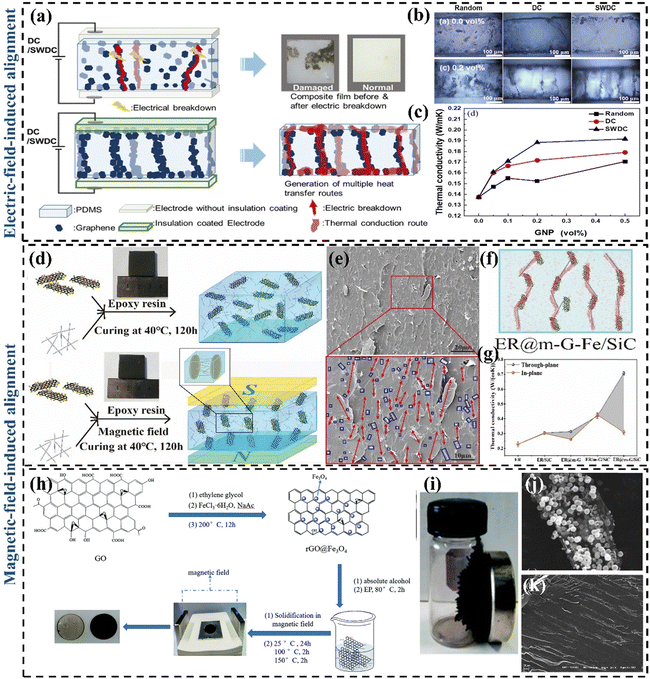 | ||
| Fig. 9 (a) Mechanism diagram of the electric field-induced alignment of graphene (Copyright©2021 Elsevier B.V. All rights reserved).147 (b) Cross-sectional digital micrographs of PDMS/GNP composites with 0.1 vol% and 0.5 vol% prepared using different electric fields (Copyright©2021 Elsevier B.V. All rights reserved).147 (c) The k of PDMS/GNP composites as a function of GNP content (Copyright©2021 Elsevier B.V. All rights reserved).147 (d) Preparation process of ER/m-graphene–Fe/SiC composites with external magnetic field (Copyright©2020 Published by Elsevier Ltd).148 (e) The cross-sectional SEM images of ER@m-graphene–Fe/SiC-3.36 wt% (the red arrows represent the m-G–Fe in ER composites; the blue circles represent the dispersion of SiC nanowires).148 (f) Schematic diagram of the cross-section of the through-surface k of the ER@m-graphene–Fe/SiC composite material.148 (g) The comparison of through-plane k and in-plane k of ER composites.148 (h) Synthesis of rGO@Fe3O4 and preparation of rGO@Fe3O4/EP.149 (i) Image of rGO@Fe3O4.149 (j) SEM images of rGO@Fe3O4 nanocomposite. (k) Cross-sectional SEM image of rGO@Fe3O4/EP parallel to the magnetic field direction.149 | ||
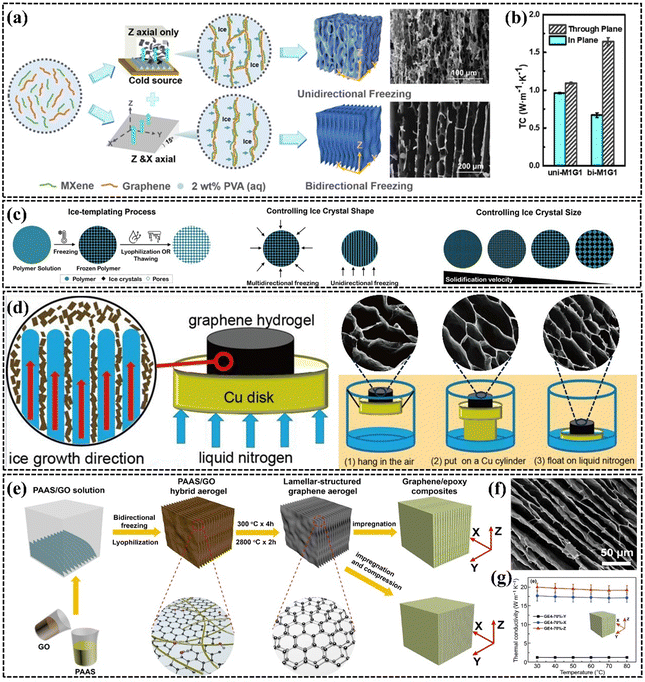 | ||
| Fig. 10 (a) and (b) Schematic structures and k values of PEG/MXene/graphene composites obtained by unidirectional and bidirectional freezing (Copyright©2021 American Chemical Society).152 (c) Effects of cooling rate, solution concentration, and viscosity on pore size and size (Copyright©2021 Wiley-VCH GmbH).153 (d) Schematic diagram and SEM images of vertically aligned graphene aerogels with different pore sizes fabricated by different directional freezing rates (Copyright©2018 Elsevier Ltd. All rights reserved).154 (e–g) Schematic illustration of the fabrication, SEM images, and k of EP/graphene composite (Copyright©2020, The Author(s)).79 | ||
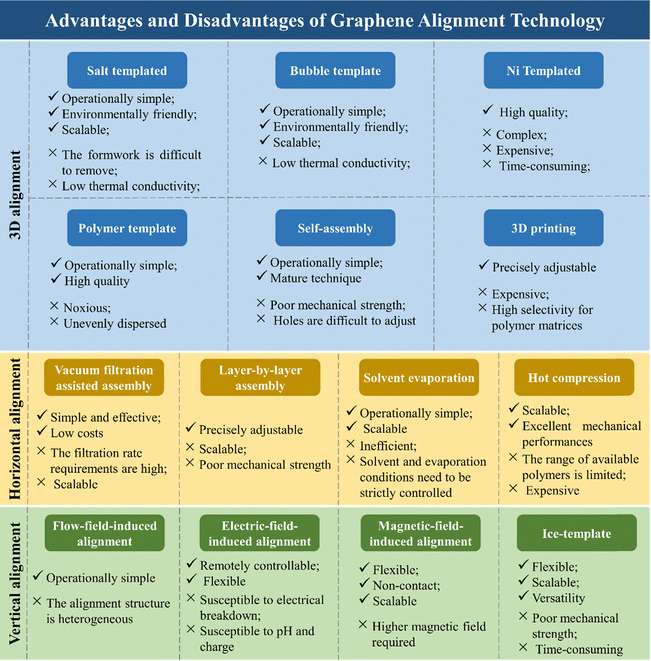
In addition to the methods mentioned above, there are numerous techniques available for aligning graphene. These methods can be interchanged or combined under appropriate conditions. Detailed literature examples and summaries of the advantages and disadvantages of these graphene alignment techniques are provided in Table 2 and Fig. 11, respectively. These summaries are helpful for researchers to understand and appropriately utilize the alignment technology of graphene.
| Method | Filler type | Filler content | k (W m−1 K−1) | Ref. | |
|---|---|---|---|---|---|
| In-plane k | Through-plane k | ||||
| Template method | rGO | 1.46 wt% | — | 1.50 | 111 |
| rGO/GNP | 18.1 wt% | — | 3 | 112 | |
| MXene/graphene | 18.7 wt% | — | 2.44 | 157 | |
| GO/GNP | — | 1.82 | 118 | ||
| Graphene | 0.86 wt% | — | 1.35 | 86 | |
| Self-assembly | GO | 2.5 wt% | — | 2.53 | 124 |
| rGO@Ni(OH)/BN | — | — | 2.01 | 104 | |
| rGO/Al2O3 | — | — | 1.68 | 158 | |
| BN/multilayer graphene | 10 wt% | — | 0.69 | 98 | |
| 3D printing | GNPS | 10.93 vol% | 4.3 | 126 | |
| Vacuum filtration-assisted assembly | Graphene/aramid nanofiber | 20 wt% | — | 20.54 | 132 |
| Alumina/graphene | 42.2 wt% | — | 13.3 | 159 | |
| BNNS/graphene/cellulose nanofiber | — | 125.0 | 2.1 | 160 | |
| Layer-by-layer self-assembly | rGO | 2.53 wt% | — | 2.03 | 134 |
| CNT/graphene | — | 1056 | 101 | ||
| Evaporation-assembled | Graphene/CNT | — | 1597 | 2.65 | 137 |
| External fields assisted alignment | GNP | 0.5 vol% | — | 0.19 | 147 |
| Ice-template | rGO@Fe3O4 | 30 wt% | 0.611 | 148 | |
| BNNS/graphene | 11.2 vol% | 2.23 | 1.09 | 154 | |
| BN/rGO | 2.30 vol% | 20.0 | 155 | ||
| GO/BNNS | — | 1.49 | 99 | ||
4. GPNs for thermal management applications
4.1 Thermal interface materials
The continuous miniaturization of electronic chips has led to a dramatic increase in concentrated heat generation power,31,161,162 which can affect the lifetime and product performance of electronic devices.163,164 The air with extremely low k present between the heat sink and the heat source can prevent electronic devices from dissipating heat efficiently, so TIM is commonly used to replace air as the heat transfer bridge between the heat source and the heat sink to effectively improve the problem of low heat dissipation efficiency (Fig. 12(a)).165 However, the TIMs with low k have emerged as a key challenge to address to guarantee the performance, longevity, and dependability of electronic devices.5,21,166,167 Ideal TIMs require both high k and good mechanical compliance. High k facilitates rapid heat transfer between the heat source and the heat sink, and good mechanical compliance ensures that the TIM adequately fills the interfacial micro void thereby reducing the contact thermal resistance. Common TIMs are mainly composed of thermally conductive fillers (e.g., Al2O3, AlN, and metal particles) and polymer (e.g. PDMS, EP, and SR),168 and there is a trade-off between k and mechanical compliance in such filling systems.169,170 Graphene is a commonly used thermally conductive filler in TIMs due to its ultra-high k and its ease of modulation into different structures from micro to macro. GPNs filled with different situations have been commonly used for thermal interface thermal conductivity applications in recent years, exhibiting high k, excellent flexibility, good processability, and low density.48,171–174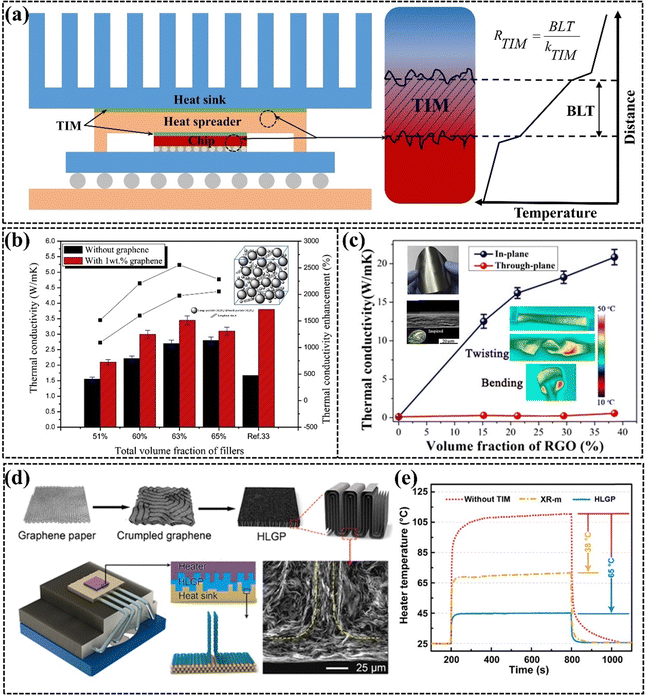 | ||
| Fig. 12 (a) Diagram of TIM materials used for chip thermal conductivity and the factors influencing their thermal conductivity. (b) Comparison of the thermal conductivity of silicone thermal grease with and without graphene, and the enhancement achieved with various filler loadings (Copyright©2015 Elsevier Masson SAS. All rights reserved).175 (c) The k of NR/RGO composite films with varying rGO content, with a thickness ranging from 16 to 22 cm (Copyright©2019 American Chemical Society).176 (d) Schematic diagram illustrating the structural changes in graphene and the thermal interface material, and (e) the temperature variation of a ceramic heating pad at an applied power of 20 W cm−2 (Copyright©2019 American Chemical Society).177 | ||
Common TIMs include both uncured and cured GPNs. Uncured TIMs are recognized for their excellent wettability and flowability, effectively filling gaps between rough surfaces. The viscosity of uncured TIMs is a critical factor influencing their thermal properties, affecting bond line thickness (BLT) and TIM volume. Lower viscosity may reduce BLT but can also lead to leakage.178 Lewis et al.166 noted that although commercially available uncured TIMs typically begin with high viscosity, the incorporation of a small amount of graphene significantly enhances thermal conductivity, as demonstrated by Yu et al., who showed that adding 1 wt% graphene to silicone grease increased its thermal conductivity from 2.70 W m−1 K−1 to 3.45 W m−1 K−1 (Fig. 12(b)).175 Cured TIMs are increasingly preferred in research due to their ease of use and no pump-out effects. They are typically available in two forms, including Graphene pads in block form and graphene paper in film form. Graphene pads are more inclined to transfer heat in the through-plane direction, and graphene needs to be arranged vertically in the matrix to form a vertical heat conduction path. The compressibility of these pads aids in eliminating trapped air between surfaces. Thin graphene paper has garnered attention for its ability to address the low heat transfer efficiency associated with thick adhesive layers in pads. The thickness of graphene paper is typically very minimal. In particular, graphene paper with a bionic nacre layer exhibits exceptionally high in-plane thermal conductivity and tensile strength. Feng et al. developed a robust synthetic nacre material by laminating rGO with natural rubber using a straightforward solution casting method. This TIM achieved an impressive heat dissipation rate of 20.84 W m−1 K−1 at a thickness of only 16–22 μm, while also demonstrating remarkable flexibility and durability, enduring over 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 tensile cycles (Fig. 12(c)).176 Graphene paper can effectively adhere to metal heat sinks, facilitating direct contact between the horizontal graphene and the metal. The superior thermal conductivity of graphene paper, coupled with its ease of large-scale production and low cost, is increasing the potential for practical applications of TIMs in academia and industry. A novel strategy to improve thermal conductivity and reduce contact thermal resistance involves machining horizontal graphene paper into highly conductive graphene pads. Dai et al. prepared layered-structured graphene composites through pleating and lateral compression, achieving a vertical alignment of graphene that resulted in a high thermal conductivity of 143 W m−1 K−1 and a low compression modulus of 0.87 MPa. The cooling efficiency of the graphene pads as a TIM was three times greater than that of leading commercial TIMs, showcasing its superior capability to address interfacial heat transfer challenges in electronic systems (Fig. 12(d) and (e)).177
000 tensile cycles (Fig. 12(c)).176 Graphene paper can effectively adhere to metal heat sinks, facilitating direct contact between the horizontal graphene and the metal. The superior thermal conductivity of graphene paper, coupled with its ease of large-scale production and low cost, is increasing the potential for practical applications of TIMs in academia and industry. A novel strategy to improve thermal conductivity and reduce contact thermal resistance involves machining horizontal graphene paper into highly conductive graphene pads. Dai et al. prepared layered-structured graphene composites through pleating and lateral compression, achieving a vertical alignment of graphene that resulted in a high thermal conductivity of 143 W m−1 K−1 and a low compression modulus of 0.87 MPa. The cooling efficiency of the graphene pads as a TIM was three times greater than that of leading commercial TIMs, showcasing its superior capability to address interfacial heat transfer challenges in electronic systems (Fig. 12(d) and (e)).177
4.2 Phase change materials
A phase change material is a type of material that undergoes a phase change at a specific temperature or pressure, and the process is usually associated with the absorption or release of a large amount of energy. Polymeric phase change materials are widely used because of their stability and wide range of phase change temperatures.179 However, the low k of PCMs is the key issue limiting their development.179,180 The efficient technique to increase the k of PCMs is to incorporate highly thermally conductive fillers,181–183 fins,184 or thermally conductive porous structures.185 Graphene nanosheets have been used to enhance the thermal properties of PCMs because of their ultra-high k and relatively low density. Different forms of graphene-based organic PCMs are often used in the thermal management of electronic devices,186,187 battery thermal management,188,189 and energy storage190–193 due to their high latent heat and lower contact thermal resistance by improving the wettability of the two contacting interfaces through the solid-to-liquid transition. For example, Li et al.174 incorporated and dispersed a mixture of sulfonated graphene (SG) as a thermally conductive enhancement material in PEG, significantly improving the k at low SG loading. To enhance the connected thermal pathway, Hussain et al.194 investigated a graphene-coated nickel (GcN) foam composite phase change material demonstrating that attaching graphene to sponge or metal foam is an effective enhancement method. The surface temperature of the battery using GcN foam composite phase change phase change material was reduced by 17% compared to using nickel foam at 1.7 A discharge current. Graphene helps to enhance the thermal storage rate of phase change materials. Cui et al. enhanced the thermal conductivity of graphene-based composite PCMs to 0.59 W m−1 K−1 and increased solar thermal storage efficiency to 79.36%. This PCM can also be utilized in a solar-powered thermoelectric conversion system, showcasing its application in clean energy (Fig. 13(a) and (b)).190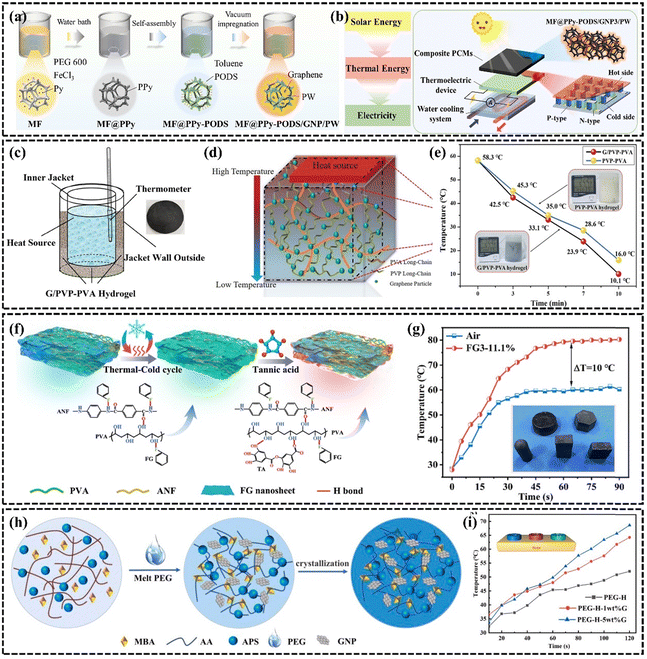 | ||
| Fig. 13 (a) Schematic illustration for the preparation process of composite PCMs (Copyright©2022 Elsevier Ltd. All rights reserved).190 (b) Experimental schematic diagram of the thermoelectric conversion system with composite PCMs driven by solar energy.190 (c) G/PVP–PVA hydrogel heat dissipation model setup (Copyright©2022 The Authors. Macromolecular Materials and Engineering published by Wiley-VCH GmbH).195 (d) Mechanism diagram of G/PVP–PVA hydrogel heat dissipation.195 (e) Comparison of heat dissipation performance of G/PVP–PVA hydrogel and PVP–PVA hydrogel.195 (f) Schematic preparation procedure of ANF–FG–PVA composite hydrogels (Copyright©2024, American Chemical Society).196 (g) Temperature versus time for LED of ANF–FG–PVA hydrogel.196 (h) Synthesis procedure of the graphene-based phase change material composite hydrogel (Copyright©2021 Elsevier Ltd. All rights reserved).197 (i) Variation curve of upper surface temperature and heating time of phase change hydrogel composite sample.197 | ||
Currently, liquid–gas PCMs with an order of magnitude higher latent heat value show a unique appeal than organic solid–liquid PCMs. Water, as a common liquid–gas phase change material with high latent heat (2500 J g−1), has tremendous advantages in heat transfer and heat dissipation. However, the susceptibility of water to leakage limits its wide application in thermal management. Hydrogel is a polymer formed by physical and chemical cross-linking. The 3D hydrogel network formed by crosslinking and entanglement of polymer chains can store up to 95% of its volume of water,198 which behaves as a good water storage matrix. In recent years, the use of hydrogels for phase change cooling has become more and more acceptable to the public. Boon-in199 prepared a dual network hydrogel of PAMPS and PNIPAM to dissipate heat by water evaporation, thus contributing to the relief of pain caused by inflammation of human skin. To accelerate the evaporation of water to achieve the effect of rapid cooling, the addition of fillers to increase the k of the hydrogel is the main method.200 Ma et al.195 constructed a highly thermally conductive graphene-based/polyvinylpyrrolidone–poly(vinyl alcohol) (G/PVP–PVA) hydrogel with an interpenetrating network by physical cross-linking and freeze-thawing combined methods (Fig. 13(c)–(e)). Due to the homogeneous dispersion of graphene in the hydrogel and the formation of thermally conductive pathways, the k of this hydrogel was as high as 1.486 W m−1 K−1, which was enhanced by 170.18% compared with the k of the conventional hydrogel (0.55 W m−1 K−1). Due to the high latent heat and high k, the cooling rate of graphene-based hydrogels is as high as 1.1 °C min−1 far higher than that of commercial gels at 0.27 °C min−1. The enhanced k of hydrogels proves to be crucial for realizing highly efficient heat transfer performance. To broaden the application of hydrogels for the thermal management of flexible electronics, Tian et al.196 created a solid–liquid interpenetrating network hydrogel (ANF-FG-PVA) with a high k of 1.42 W m−1 K−1, composed of aromatic polyamide nanofibers, fluorinated graphene, and PVA (Fig. 13(f) and (g)). The hydrogel significantly reduced the operating temperature in the thermal performance test of LEDs. The composite of PCM and hydrogel is also a new PCM. Yang et al.197 incorporated solid–liquid phase change materials into a graphene-based hydrogel and designed a phase change composite with low contact thermal resistance and high k. The crosslinked network of the hydrogel solves the leakage problem of the phase change material, and the addition of graphene helps to enhance the k and thermal stability of the composite (Fig. 13(h) and (i)). These approaches are anticipated to significantly advance the development of PCM in the field of thermal management.
4.3 Intelligent responsive thermal management materials
A great deal of research has been done on flexible GPNs with high k, which have displayed good potential for thermal management material applications in many fields. However, with the development of microelectronics and other technologies, the smartness of the materials has also become a popular pursuit. It has been proposed that GPN films can be endowed with intelligence by employing shape memory polymers. For example, polyvinyl alcohol is commonly used as a thermally responsive shape memory material, with nanofibrillated cellulose supporting and encapsulating the PEG, and a regular arrangement of graphene to enhance k. The incorporation of 30 wt% graphene significantly improves the thermal conductivity of GPN films, increasing it to 21.83 W m−1 K−1. The shape memory polymer with high k is applied to the back of the LED as a lateral heat spreader, effectively reducing the temperature of the LED system and slowing its heating rate, thereby protecting and extending the lifespan of the electronics. Furthermore, the shape memory film begins to expand at 60 °C, providing a visual warning that the LED is overheating. This shape memory polymer exhibits different folding degrees with temperature changes and accelerates the reduction of LED operating temperature, demonstrating excellent capability for smart thermal management (Fig. 14(a)).201,202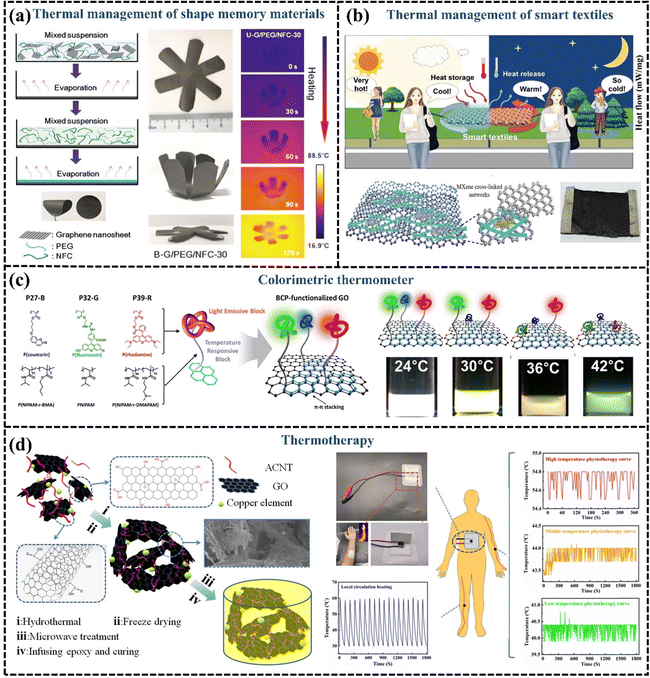 | ||
| Fig. 14 (a) Schematic illustration of the evaporation-induced self-assembly process and shape memory behaviors of the hybrid films (Copyright©2019 American Chemical Society).201 (b) Schematic illustration of the heat storage and temperature regulation of PCM-integrated smart textile (Copyright©2023 Wiley-VCH GmbH).203 (c) Schematic illustration of the colorimetric thermometer (Copyright©2016, American Chemical Society).204 (d) Diagrammatic preparation processing and hyperthermia application of the GO–CNT/EP nanocomposites (Copyright©2021 Wiley-VCH GmbH).205 | ||
GPNs are not only used for thermal management in smart electronic devices but are also widely applied in smart textiles. Circuits in wearable electronic devices or electronic smart textiles generate heat during operation, which requires the enhancement of material thermal conductivity for thermal management. The incorporation of graphene with high k into conventional textiles can be used for heat dissipation and adaptive cooling.206 Yang et al. developed a graphene paper with high out-of-plane k, flexibility, and a large ultra-thin surface area. They demonstrated that this graphene paper can be utilized as a wearable fabric, exhibiting excellent cooling capabilities under moderate temperature conditions (15–30 °C). Due to its high k, graphene paper facilitates passive cooling by transferring heat from the body to the environment. This innovative material significantly reduces the cooling response time for individuals, decreasing it from 150 seconds to just 7 seconds when compared to conventional cotton fabrics, highlighting its substantial potential for human body cooling.207 In addition to its applications in body cooling, smart textiles made from GPNs also show considerable promise in temperature regulation. Chen et al. assembled 1D AgNWs, 2D MXene, and graphene on PU fibers LBL alternately to prepare and obtain a smart textile, which exhibited a fast response to both electrical and optical stimuli due to fast electron/phonon transport conferred by graphene. Smart responsive textiles integrated with PCMs can release stored solar energy during the night or on rainy days, enabling continuous self-powered thermoregulation (Fig. 14(b)).203
Smart responsive GPNs are also being continuously pioneered for applications in other special scenarios for thermal management. Lee et al.204 developed a colorimetric thermometer based on block copolymer-functionalized graphene, where different block copolymers provide different color display responses as the temperature changes, demonstrating the potential of this material for fluorescent thermo-responsive switching or sensor applications (Fig. 14(c)). In recent years thermotherapy has become one of the common means used to induce the death of cancer cells and enhance the effect of radiotherapy. Wang et al.205 designed a poly(vinyl alcohol) aerogel consisting of a combination of GO, acidified CNTs, and copper particles as a reinforcement material, which had efficient electrical heating properties, rapid thermal responsiveness, and temperature stability, and the temperature was always maintained in high-temperature thermotherapy at 54.4–54.8 °C. Thus, thermo-responsive GPNs can fulfill the requirements of thermotherapy devices and have the potential for use in the field of thermotherapy (Fig. 14(d)).
5. Conclusions and perspectives
The recent progress in the study of the thermal conductivity of GPNs in recent years is presented from three primary perspectives. This aims to offer insights for the development of the next generation of highly thermally conductive polymer composites that can effectively meet the demand for efficient heat dissipation. In the first part, the primary focus is on a microscopic perspective to analyze the effect of graphene nanosheets on the k of GPNs. The effects of structural parameters of graphene (e.g., defects, size, and number of layers) on the intrinsic k of graphene are presented. Common strategies used in recent years to modulate the structural parameters, defects, and surface states of graphene are summarized. These strategies include the exfoliation and preparation of graphene, defect engineering, and surface modification. The distribution state of graphene in the polymer matrix and the effect on thermal conductivity are also fully discussed. In the second part, the discussion primarily adopts a macro perspective. We summarize the preparation of macroscopic thermally conductive structures in GPNs, including hybridization of thermally conductive fillers, 3D network alignment, horizontal alignment, and vertical alignment. The hybridization includes the strategy of hybridizing graphene nanosheets with 0D, 1D, and 2D thermally conductive fillers, respectively, all of which exhibit synergistic effects in the polymer composites. This is because multiple fillers with different shapes can enhance each other's dispersion and enable the construction of thermally conductive pathways by bridging and filling the voids. 3D network alignment, horizontal alignment, and vertical alignment allow the construction of continuous thermally conductive pathways in polymers, overcoming the large thermal resistance caused by discontinuous fillers. In the third part, we summarize some recent applications of GPNs as TIMs, PCMs, and smart responsive thermal management materials in the field of thermal management. Although significant progress has been made in recent years to enhance the k of GPNs through both micro- and macro-level strategies, there remains considerable opportunity for future research and development.(1) Graphene is challenging to disperse effectively. To enhance its dispersibility, functionalization is often employed. However, this approach can introduce defects that increase phonon scattering within the graphene structure. A common alternative is the reduced GO, which aims to improve dispersibility while minimizing defects. Unfortunately, this method typically only partially restores the thermal conductivity of graphene. Additionally, new defects may arise during the reduction process, or the original graphene layer may become inhomogeneous, adversely affecting the material's overall performance. Consequently, the pursuit of improved graphene dispersion while maintaining its intrinsic thermal conductivity is a critical focus in the advancement of GPNs.
(2) In numerous studies, it is evident that authors lack stringent criteria for defining graphene. For instance, graphene can be categorized based on the number of layers into single-layer graphene, double-layer graphene, and multi-layer graphene, etc. However, the current definitions of these categories remain rather ambiguous. Additionally, graphene can be classified according to its functionalization into graphene, GO, and rGO. Nevertheless, many researchers may collectively refer to all of these as graphene in their descriptions. Each type of graphene possesses distinct properties that may be suitable for various applications. The absence of standardized information can mislead or confuse readers, thereby impeding the advancement of research. Consequently, the accurate selection of the appropriate type of graphene is essential for success, and the standardization of graphene definitions is particularly urgent.
(3) Model the thermal conductivity pathways of graphene. Parameters such as the length and thickness of the pathway are calculated by constructing a topological model to find the optimal solution or trend. Theoretical guidance can be given to practical experiments through calculations and simulations, which can greatly improve the research efficiency.
(4) In practical applications, thermal conductivity is not the unique indicator for assessing the quality of GPNs. At present, many researchers are overly focused on achieving high k, often neglecting the importance of other essential properties. In thermal management applications, factors such as thermal stability, heat resistance, mechanical properties, coefficient of thermal expansion, and interfacial characteristics also play a crucial role. For instance, commonly used TIM materials often require both high thermal conductivity and excellent mechanical compliance to ensure efficient heat transport under high packaging pressures. Therefore, when evaluating a material's performance, it is vital to consider multiple parameters and real-world application scenarios to obtain a comprehensive understanding of its behavior under specific conditions. This multidimensional evaluation approach will facilitate more accurate selection and design of materials to meet specific requirements.
(5) The multifunctional integration of GPNs is crucial for enhancing their performance and expanding their range of applications. By incorporating various functions and properties into a single material, it becomes possible to satisfy the increasingly stringent demands for material performance in contemporary society. For instance, imparting self-healing and adhesion properties to GPNs can significantly improve their heat transfer stability during use, thereby greatly reducing the risks associated with accidental damage. Thus, multifunctional integrated GPNs will further broaden the range of applications for GPNs.
Data availability
No primary research results, software or code have been included and no new data were generated or analysed as part of this review.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge financial support from the National Natural Science Foundation of China (grant no. 52375221 and 52105229).References
- Z. Yuan, H. Ma, M. A. Hussien and Y. Feng, Macromol. Mater. Eng., 2021, 306, 2100428 CrossRef CAS.
- X. Zhang, Z. Ji, J. Wang and X. Lv, Appl. Therm. Eng., 2023, 235, 121294 CrossRef.
- L. Lv, J. Ying, L. Chen, P. Tao, L. Sun, K. Yang, L. Fu, J. Yu, Q. Yan, W. Dai, N. Jiang and C.-T. Lin, Nanomaterials, 2023, 13, 793 CrossRef CAS.
- J. Janting, J. G. Theander and H. Egesborg, IEEE Trans. Device Mater. Reliab., 2019, 19, 313–321 CAS.
- J. Chen, X. Huang, B. Sun and P. Jiang, ACS Nano, 2019, 13, 337–345 CrossRef CAS PubMed.
- F. Tarannum, R. Muthaiah, R. S. Annam, T. Gu and J. Garg, Nanomaterials, 2020, 10, 1291 CAS.
- C. Huang, X. Qian and R. Yang, Mater. Sci. Eng., R, 2018, 132, 1–22 Search PubMed.
- C. Zhu, T. Liu, F. Qian, T. Y.-J. Han, E. B. Duoss, J. D. Kuntz, C. M. Spadaccini, M. A. Worsley and Y. Li, Nano Lett., 2016, 16, 3448–3456 CAS.
- D. Li, T. Li, Z. Mao, Y. Zhang and B. Wang, RSC Adv., 2023, 13, 27599–27607 RSC.
- A. K. Tareen, K. Khan, M. Iqbal, Y. Zhang, J. Long, F. Nazeer, A. Mahmood, N. Mahmood, Z. Shi, C. Ma, W. Huan, M. F. Khan, J. Yin, C. Li and H. Zhang, J. Mater. Chem. C, 2022, 10, 11472–11531 RSC.
- Y. Zhu, Y. Ming, J. Sun, S. Li, S. Li, H. Xiao, B. Wang and Y. Duan, Chem. Eng. J., 2023, 474, 145583 CrossRef CAS.
- S. Wan, L. Jiang and Q. Cheng, Matter, 2020, 3, 696–707 CrossRef.
- M. Usman, I.-H. Kim and H.-J. Jung, AIP Adv., 2016, 6, 055027 CrossRef.
- X. Zhang and P. Samorì, ChemNanoMat, 2017, 3, 362–372 CAS.
- Q. Guo, J. Guo, H. Chen, P. Zhou, C. Li, K. Yang, N. Hua, J. Wang and M. Weng, J. Mater. Chem. A, 2023, 11, 11773–11785 Search PubMed.
- X. Huang, C. Zhi, Y. Lin, H. Bao, G. Wu, P. Jiang and Y.-W. Mai, Mater. Sci. Eng., R, 2020, 142, 100577 Search PubMed.
- J. Chen and J. Han, Results Phys., 2019, 15, 102803 Search PubMed.
- J. Chen, X. Gao and W. Song, Results Phys., 2019, 15, 102771 Search PubMed.
- S. Wilczewski, K. Skórczewska, J. Tomaszewska, M. Osial, A. Dąbrowska, K. Nikiforow, P. Jenczyk and H. Grzywacz, Molecules, 2023, 28, 3383 CrossRef CAS PubMed.
- P. Govindaraj, A. Sokolova, N. Salim, S. Juodkazis, F. K. Fuss, B. Fox and N. Hameed, Composites, Part B, 2021, 226, 109353 CAS.
- Z. Wang, Z. Wu, L. Weng, S. Ge, D. Jiang, M. Huang, D. M. Mulvihill, Q. Chen, Z. Guo, A. Jazzar, X. He, X. Zhang and B. B. Xu, Adv. Funct. Mater., 2023, 33, 2301549 CAS.
- F. Zhang, Y. Feng and W. Feng, Mater. Sci. Eng., R, 2020, 142, 100580 Search PubMed.
- P. Liu, L. Wang, B. Cao, L. Li, K.-L. Zhang, X.-M. Bian and Z.-L. Hou, J. Mater. Chem. C, 2017, 5, 6745–6754 RSC.
- Q. Kong, X. Shi, W. Ma, F. Zhang, T. Yu, F. Zhao, D. Zhao and C. Wei, J. Hazard. Mater., 2021, 415, 125690 CrossRef CAS PubMed.
- H. Chen, V. V. Ginzburg, J. Yang, Y. Yang, W. Liu, Y. Huang, L. Du and B. Chen, Prog. Polym. Sci., 2016, 59, 41–85 CrossRef CAS.
- R. Wang, C. Xie, B. Gou, H. Xu, S. Luo, J. Zhou and L. Zeng, Polym. Test., 2020, 89, 106574 CrossRef CAS.
- N. Burger, A. Laachachi, M. Ferriol, M. Lutz, V. Toniazzo and D. Ruch, Prog. Polym. Sci., 2016, 61, 1–28 CrossRef CAS.
- H. Kim, G. Park, S. Park and W. Kim, ACS Nano, 2021, 15, 2182–2196 CrossRef CAS PubMed.
- Y. Zhang, Q. Wan and N. Yang, Small, 2019, 15, 1903780 CrossRef CAS.
- J. Chen and B. Liu, Phys. E, 2022, 139, 115146 CrossRef CAS.
- J. Ying, W. Dai, J. Yu, N. Jiang, C.-T. Lin and Q. Yan, Sci. China: Phys., Mech. Astron., 2022, 65, 117005 CAS.
- Z. Ma, Z. Guo, H. Zhang and T. Chang, AIP Adv., 2017, 7, 065104 CrossRef.
- R. Muthaiah, F. Tarannum, S. Danayat, R. S. Annam, A. S. Nayal, N. Yedukondalu and J. Garg, Phys. Chem. Chem. Phys., 2022, 24, 14640–14650 RSC.
- H.-Y. Cao, Z.-X. Guo, H. Xiang and X.-G. Gong, Phys. Lett. A, 2012, 376, 525–528 CrossRef CAS.
- R. Su and X. Zhang, Appl. Therm. Eng., 2018, 144, 488–494 CrossRef CAS.
- M. Li, H. Zhou, Y. Zhang, Y. Liao and H. Zhou, Carbon, 2018, 130, 295–303 CrossRef CAS.
- B. S. Lee, J. Phys.: Condens. Matter, 2018, 30, 295302 CrossRef PubMed.
- H. Wang, K. Kurata, T. Fukunaga, X. Zhang and H. Takamatsu, Int. J. Heat Mass Transfer, 2017, 105, 76–80 CrossRef CAS.
- M. D. Bhatt, H. Kim and G. Kim, RSC Adv., 2022, 12, 21520–21547 RSC.
- F. Banhart, J. Kotakoski and A. V. Krasheninnikov, ACS Nano, 2011, 5, 26–41 CrossRef CAS.
- A. Fox, U. Ray and T. Li, J. Appl. Phys., 2018, 125, 015101 CrossRef.
- X.-F. Peng, X. Zhou, S.-H. Tan, X.-J. Wang, L.-Q. Chen and K.-Q. Chen, Carbon, 2017, 113, 334–339 CrossRef CAS.
- B. Mortazavi and S. Ahzi, Carbon, 2013, 63, 460–470 CrossRef CAS.
- N. Khosravian, M. K. Samani, G. C. Loh, G. C. K. Chen, D. Baillargeat and B. K. Tay, Comput. Mater. Sci., 2013, 79, 132–135 CrossRef CAS.
- J. Wang, C. Li, Y. Sheng, Y. Su and L. Yang, Appl. Phys. Lett., 2022, 121, 042202 CrossRef CAS.
- H. Guo, B. Hu, Q. Wang, J. Liu, M. Li and B. Li, Appl. Surf. Sci., 2023, 615, 156404 Search PubMed.
- G. Chang, L. Wang, Y. Zhang, X. Li, K. Chen, D. Kan, W. Zhang, S. Zhang, L. Dong, L. Li, X. Bai, H. Zhang and W. Huo, ACS Appl. Mater. Interfaces, 2022, 14, 56156–56168 CrossRef CAS PubMed.
- W. Liang, X. Ge, J. Ge, T. Li, T. Zhao, X. Chen, M. Zhang, J. Ji, X. Pang and R. Liu, Nanomaterials, 2019, 9, 938 Search PubMed.
- J. Zhang, T. Chen, S. Liu, Z. Chen, Y. Li, S. Zhu and H. Li, J. Mater. Chem. A, 2021, 9, 27529–27540 CAS.
- J. Gu and K. Ruan, Nano-Micro Lett., 2021, 13, 110 Search PubMed.
- J. Wang, P. Ren, F. Ren, G. Zhu, A. Sun and C. You, J. Mater. Sci., 2021, 56, 7951–7965 CAS.
- S. Lin and M. J. Buehler, Nanotechnology, 2013, 24, 165702 CrossRef PubMed.
- G. Yang, L. Sang, D. R. G. Mitchell, F. Fei Yun, K. Wai See, A. Jumlat Ahmed, S. Sayyar, A. Bake, P. Liu, L. Chen, Z. Yue, D. Cortie and X. Wang, Chem. Eng. J., 2022, 428, 131205 CAS.
- T. Zhou, Y. Du, C. Zhao, Y. Wang and J. Zhao, Int. J. Energy Res., 2020, 44, 1062–1077 Search PubMed.
- C. Zhan, W. Cui, L. Li, X. Quan, Y. Zhang and F. Xiao, Compos. Sci. Technol., 2023, 231, 109823 CAS.
- T. Ma, K. Ruan, Y. Guo, Y. Han and J. Gu, Sci. China Mater., 2023, 66, 4012–4021 Search PubMed.
- A. Chatterjee, R. Verma, H. P. Umashankar, S. Kasthurirengan, N. C. Shivaprakash and U. Behera, Int. J. Therm. Sci., 2019, 136, 389–395 CAS.
- J.-u Jang, S. O. So, J. H. Kim, S. Y. Kim and S. H. Kim, Compos. Commun., 2022, 31, 101110 Search PubMed.
- X. Yang, C. Liang, T. Ma, Y. Guo, J. Kong, J. Gu, M. Chen and J. Zhu, Adv. Compos. Hybrid Mater., 2018, 1, 207–230 Search PubMed.
- J.-u Jang, H. E. Nam, S. O. So, H. Lee, G. S. Kim, S. Y. Kim and S. H. Kim, Polymers, 2022, 14, 323 Search PubMed.
- F. Kargar, Z. Barani, R. Salgado, B. Debnath, J. S. Lewis, E. Aytan, R. K. Lake and A. A. Balandin, ACS Appl. Mater. Interfaces, 2018, 10, 37555–37565 CAS.
- M. Moniruzzaman and K. I. Winey, Macromolecules, 2006, 39, 5194–5205 CAS.
- X. Shen, Z. Wang, Y. Wu, X. Liu, Y.-B. He and J.-K. Kim, Nano Lett., 2016, 16, 3585–3593 CrossRef CAS.
- A. Wei, Y. Li, W. Ren and W. Ye, Appl. Phys. Lett., 2019, 114, 021902 CrossRef.
- B. Li and W.-H. Zhong, J. Mater. Sci., 2011, 46, 5595–5614 CrossRef CAS.
- J. Song and Y. Zhang, Int. J. Heat Mass Transfer, 2019, 141, 1049–1055 CrossRef CAS.
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669 CrossRef CAS PubMed.
- Y.-C. Han, S.-H. Yin, J.-R. Zheng, Y.-F. Hu, L. Sun, L. Zhang, Z.-Q. Tian and J. Yi, Adv. Funct. Mater., 2024, 34, 2307298 CAS.
- X. Li, L. Colombo and R. S. Ruoff, Adv. Mater., 2016, 28, 6247–6252 CAS.
- L. Dong, J. Yang, M. Chhowalla and K. P. Loh, Chem. Soc. Rev., 2017, 46, 7306–7316 RSC.
- C. Xu, R.-S. Yuan and X. Wang, Carbon, 2014, 71, 345 CAS.
- L. Zhang, H. Jiao, H. Jiu, J. Chang, S. Zhang and Y. Zhao, Composites, Part A, 2016, 90, 286–295 CAS.
- X. Xue, Y. Chen, Q. Yin, X. Zhang, W. Zhang, H. Jia, L. Xiao and L. Hong, Polym. Int., 2018, 67, 1401–1409 CrossRef CAS.
- N.-J. Song, C.-M. Chen, C. Lu, Z. Liu, Q.-Q. Kong and R. Cai, J. Mater. Chem. A, 2014, 2, 16563–16568 CAS.
- B.-Y. Ju, W.-S. Yang, Q. Zhang, M. Hussain, Z.-Y. Xiu, J. Qiao and G.-H. Wu, Int. J. Miner., Metall. Mater., 2020, 27, 1179–1190 CrossRef.
- I. N. Kholmanov, J. Edgeworth, E. Cavaliere, L. Gavioli, C. Magnuson and R. S. Ruoff, Adv. Mater., 2011, 23, 1675–1678 CrossRef CAS PubMed.
- B. Wang and S. T. Pantelides, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 245403 CrossRef.
- G. Xin, T. Yao, H. Sun, S. M. Scott, D. Shao, G. Wang and J. Lian, Science, 2015, 349, 1083–1087 CrossRef CAS.
- P. Liu, X. Li, P. Min, X. Chang, C. Shu, Y. Ding and Z.-Z. Yu, Nano-Micro Lett., 2020, 13, 22 CrossRef.
- K. K. H. De Silva, H.-H. Huang, R. Joshi and M. Yoshimura, Carbon, 2020, 166, 74–90 CrossRef CAS.
- F. An, X. Li, P. Min, P. Liu, Z.-G. Jiang and Z.-Z. Yu, ACS Appl. Mater. Interfaces, 2018, 10, 17383–17392 CrossRef CAS.
- T.-Y. Wang and J.-L. Tsai, Comput. Mater. Sci., 2016, 122, 272–280 CrossRef CAS.
- W. Yu, L. Sisi, Y. Haiyan and L. Jie, RSC Adv., 2020, 10, 15328–15345 RSC.
- X. Shen, Z. Wang, Y. Wu, X. Liu and J.-K. Kim, Carbon, 2016, 108, 412–422 CrossRef CAS.
- A. Chandrashekar, M. Hegde, S. Krishna, J. Ayippadath Gopi, T. M. Kotresh and T. N. Prabhu, Eur. Polym. J., 2023, 198, 112379 CrossRef CAS.
- J. Gong, X. Tan, Q. Yuan, Z. Liu, J. Ying, L. Lv, Q. Yan, W. Chu, C. Xue, J. Yu, K. Nishimura, N. Jiang, C.-T. Lin and W. Dai, Chin. J. Chem., 2022, 40, 329–336 CrossRef CAS.
- M. Qin, Y. Xu, R. Cao, W. Feng and L. Chen, Adv. Funct. Mater., 2018, 28, 1805053 CrossRef.
- M.-Y. Song, C.-G. Ma, X.-L. Li, H.-T. Chi, P. Zhang and P.-B. Dai, Polym. Compos., 2023, 44, 6136–6148 CrossRef CAS.
- J. Huang, W. Yang, J. Zhu, L. Fu, D. Li and L. Zhou, Composites, Part A, 2019, 123, 79–85 CrossRef CAS.
- F. Jiang, X. Cui, N. Song, L. Shi and P. Ding, Compos. Commun., 2020, 20, 100350 CrossRef.
- X. Zhang, J. Song, J. Meng and K. Zhang, Materials, 2022, 15, 8078 CrossRef CAS.
- Z. Barani, A. Mohammadzadeh, A. Geremew, C.-Y. Huang, D. Coleman, L. Mangolini, F. Kargar and A. A. Balandin, Adv. Funct. Mater., 2020, 30, 1904008 CrossRef CAS.
- C. Shen, H. Wang, T. Zhang and Y. Zeng, J. Mater. Sci. Technol., 2019, 35, 36–43 CrossRef CAS.
- R. Lv, H. Guo, L. Kang, A. Bashir, L. Ren, H. Niu and S. Bai, Nanomaterials, 2023, 13, 2243 CrossRef CAS.
- H. Wu, W. Zhou, Q. Liu, X. Cai, Z. Qu, P. Li, D. Hu and X. Jia, J. Appl. Polym. Sci., 2022, 139, 51838 CrossRef CAS.
- K. Xiong, C. Ma, J. Wang, X. Ge, W. Qiao and L. Ling, Ceram. Int., 2023, 49, 8847–8855 CrossRef CAS.
- S. Lin, H. Yang, Y. Shen and P. Yang, Eur. Polym. J., 2024, 202, 112632 CrossRef CAS.
- B. Deng, Y. Shi, X. Zhang, W. Ma, H. Liu and C. Gong, Nanomaterials, 2022, 12, 2335 CrossRef CAS.
- F. Guo, X. Shen, J. Zhou, D. Liu, Q. Zheng, J. Yang, B. Jia, A. K. T. Lau and J.-K. Kim, Adv. Funct. Mater., 2020, 30, 1910826 CrossRef CAS.
- Y.-Z. Xing, M. Li, H. Jia, L.-J. Xie, D. Liu, Z. Wang, Z.-C. Tao, Y.-L. Tong, Q.-Q. Kong and C.-M. Chen, J. Mater. Chem. C, 2024, 12, 1851–1859 RSC.
- D. Hu, W. Gong, J. Di, D. Li, R. Li, W. Lu, B. Gu, B. Sun and Q. Li, Carbon, 2017, 118, 659–665 CrossRef CAS.
- G. K. Dimitrakakis, E. Tylianakis and G. E. Froudakis, Nano Lett., 2008, 8, 3166–3170 CrossRef CAS.
- Z. Xu, L. Bai, Y. Zhang, J. Cao and J. Zheng, Compos. Sci. Technol., 2023, 240, 110076 CrossRef CAS.
- Y. Feng, G. Han, B. Wang, X. Zhou, J. Ma, Y. Ye, C. Liu and X. Xie, Chem. Eng. J., 2020, 379, 122402 CrossRef CAS.
- S. Chen, R. Xu, J. Liu, X. Zou, L. Qiu, F. Kang, B. Liu and H.-M. Cheng, Adv. Mater., 2019, 31, 1804810 CrossRef PubMed.
- D. Suh, C. M. Moon, D. Kim and S. Baik, Adv. Mater., 2016, 28, 7220–7227 CAS.
- X. Du, W. Yang, J. Zhu, L. Fu, D. Li and L. Zhou, Compos. Sci. Technol., 2022, 222, 109370 CrossRef CAS.
- B. Xie, W. Zhao, X. Luo and R. Hu, Mater. Sci. Eng., R, 2023, 154, 100738 CrossRef.
- H. Ma, B. Gao, M. Wang, Z. Yuan, J. Shen, J. Zhao and Y. Feng, J. Mater. Sci., 2021, 56, 1064–1086 CrossRef CAS.
- S. Li, W. Wu, D. Drummer, Y. Wang, Z. Lu and X. Zhao, Polym. Compos., 2023, 44, 5369–5380 CrossRef CAS.
- S. Song, J. Wang, C. Liu, J. Wang and Y. Zhang, Nanoscale, 2019, 11, 15234–15244 RSC.
- J. Li, X. Zhao, W. Wu, X. Ji, Y. Lu and L. Zhang, Chem. Eng. J., 2021, 415, 129054 CrossRef CAS.
- Z. Wang, X. Wang, Z. Zhang, L. Liang, Z. Zhao and J. Shi, Polym. Compos., 2023, 44, 3610–3621 CrossRef CAS.
- K. Ba, M. Zhang, X. Wang, P. Xu, W. Song, C. Wang, W. Yang and Y. Liu, Diamond Relat. Mater., 2023, 131, 109585 CrossRef CAS.
- J. Jiang, H. Sun, J. ShangGuan, F. Fu, X. Liu and S. Zhao, ACS Appl. Mater. Interfaces, 2022, 14, 43815–43824 CrossRef CAS.
- L. Pedrazzetti, E. Gibertini, F. Bizzoni, V. Russo, A. Lucotti, L. Nobili and L. Magagnin, Materials, 2022, 15, 1572 CrossRef CAS.
- Z. Chen, W. Ren, L. Gao, B. Liu, S. Pei and H.-M. Cheng, Nat. Mater., 2011, 10, 424–428 CrossRef CAS PubMed.
- J. Yang, G.-Q. Qi, R.-Y. Bao, K. Yi, M. Li, L. Peng, Z. Cai, M.-B. Yang, D. Wei and W. Yang, Energy Storage Mater., 2018, 13, 88–95 CrossRef.
- J. Yang, X. Shen, W. Yang and J. K. Kim, Prog. Mater. Sci., 2023, 133, 101054 CrossRef CAS.
- Z. Liu, Y. Chen, Y. Li, W. Dai, Q. Yan, F. E. Alam, S. Du, Z. Wang, K. Nishimura, N. Jiang, C.-T. Lin and J. Yu, Nanoscale, 2019, 11, 17600–17606 RSC.
- C. Zhu, X. Lu, H. Wu, X. Hu, X. Li, S. Liu and J.-P. Qu, Compos. Sci. Technol., 2022, 226, 109532 CAS.
- W. Dai, Y. Wang, M. Li, L. Chen, Q. Yan, J. Yu, N. Jiang and C.-T. Lin, Adv. Mater., 2024, 36, 2311335 CrossRef CAS PubMed.
- Z. Yuan, X. Xiao, J. Li, Z. Zhao, D. Yu and Q. Li, Adv. Sci., 2018, 5, 1700626 CrossRef.
- S. Cui, W. Wu, C. Liu, Y. Wang, Q. Chen and X. Liu, Nanoscale, 2021, 13, 18247–18255 RSC.
- C. Zhang, R. Huang, P. Wang, Y. Wang, Z. Zhou, H. Zhang, Z. Wu and L. Li, ACS Appl. Mater. Interfaces, 2020, 12, 58170–58178 CrossRef CAS.
- Q. Lv, Z. Peng, Y. Meng, H. Pei, Y. Chen, E. Ivanov and R. Kotsilkova, Ind. Eng. Chem. Res., 2022, 61, 16733–16746 CrossRef CAS.
- J. Zhou, X. Wu, Y. Chen, C. Yang, R. Yang, J. Tan, Y. Liu, L. Qiu and H.-M. Cheng, Adv. Funct. Mater., 2022, 32, 2105879 CrossRef CAS.
- S. Wang, H. He, X. Ye, R. Chen, Q. Li and B. Huang, Compos. Sci. Technol., 2022, 227, 109591 CrossRef CAS.
- Z. Peng, Q. Lv, J. Jing, H. Pei, Y. Chen and E. Ivanov, Composites, Part B, 2023, 251, 110491 CrossRef CAS.
- Y. Wang, Z. Xu, D. Wu and J. Bai, Materials, 2020, 13, 2406 CrossRef CAS.
- F. Zhang, C. Ye, W. Dai, L. Le, Q. Yuan, K. W. A. Chee, Y. Ke, N. Jiang, C.-T. Lin, Z. Zhan, D. Dai and L. He, Chin. Chem. Lett., 2020, 31, 244–248 CrossRef CAS.
- X. He, K. Zhang, H. Wang, Y. Zhang, G. Xiao, H. Niu and Y. Yao, Carbon, 2022, 199, 367–378 CrossRef CAS.
- J. Zhu, H. Zhang and N. A. Kotov, ACS Nano, 2013, 7, 4818–4829 CrossRef CAS PubMed.
- J. Song, C. Chen and Y. Zhang, Composites, Part A, 2018, 105, 1–8 CrossRef CAS.
- N. Song, D. Jiao, S. Cui, X. Hou, P. Ding and L. Shi, ACS Appl. Mater. Interfaces, 2017, 9, 2924–2932 CrossRef CAS.
- H. Zhu, H. Cao, X. Liu, M. Wang, X. Meng, Q. Zhou and L. Xu, Mater. Des., 2019, 175, 107783 CrossRef.
- R. Zou, F. Liu, N. Hu, H. Ning, Y. Gong, S. Wang, K. Huang, X. Jiang, C. Xu, S. Fu, Y. Li and C. Yan, ACS Appl. Mater. Interfaces, 2020, 12, 57391–57400 CrossRef CAS.
- K. E. Shopsowitz, H. Qi, W. Y. Hamad and M. J. MacLachlan, Nature, 2010, 468, 422–425 CrossRef CAS.
- H. Zeng, J. Wu, Y. Ma, Y. Ye, J. Liu, X. Li, Y. Wang, Y. Liao, X. Luo, X. Xie and Y.-W. Mai, ACS Appl. Mater. Interfaces, 2018, 10, 41690–41698 CrossRef CAS.
- P. Ding, J. Zhang, N. Song, S. Tang, Y. Liu and L. Shi, Compos. Sci. Technol., 2015, 109, 25–31 CrossRef CAS.
- Y. Lin, J. Chen, S. Dong, G. Wu, P. Jiang and X. Huang, J. Mater. Sci. Technol., 2021, 83, 219–227 CrossRef CAS.
- Z. Zhang, J. Qu, Y. Feng and W. Feng, Compos. Commun., 2018, 9, 33–41 CrossRef.
- V. Ghai, S. Pandit, M. Svensso, R. Larsson, A. Matic, R. Ngaloy, S. P. Dash, A. Terry, K. Nygård, I. Mijakovic and R. Kádár, Adv. Funct. Mater., 2024, 2406875 CrossRef CAS.
- A. Sierra-Romero and B. Chen, Nanocomposites, 2018, 4, 137–155 CrossRef CAS.
- M. Monti, M. Natali, L. Torre and J. M. Kenny, Carbon, 2012, 50, 2453–2464 CrossRef CAS.
- C.-S. Lim, A. J. Rodriguez, M. E. Guzman, J. D. Schaefer and B. Minaie, Carbon, 2011, 49, 1873–1883 CrossRef CAS.
- K.-R. Park, H.-B. Cho, M. Lim, B. K. Jang, J. Lee, B. Jeon and Y.-H. Choa, Appl. Surf. Sci., 2021, 551, 149201 CrossRef CAS.
- J. He, H. Wang, Q. Qu, Z. Su, T. Qin and X. Tian, Composites, Part A, 2020, 139, 106062 CrossRef CAS.
- J. Geng, Y. Men, C. Liu, X. Ge and C. Yuan, RSC Adv., 2021, 11, 16592–16599 RSC.
- M. Li, X. Dai, W. Gao and H. Bai, Acc. Mater. Res., 2022, 3, 1173–1185 CrossRef CAS.
- M. Li, X. Dai, M. Wang and H. Bai, Small Methods, 2024, 8, 2300213 CrossRef CAS PubMed.
- L. Jin, P. Wang, W. Cao, N. Song and P. Ding, ACS Appl. Mater. Interfaces, 2022, 14, 1747–1756 CrossRef CAS.
- H. Joukhdar, A. Seifert, T. Jüngst, J. Groll, M. S. Lord and J. Rnjak-Kovacina, Adv. Mater., 2021, 33, 2100091 CrossRef CAS PubMed.
- X.-H. Li, P. Liu, X. Li, F. An, P. Min, K.-N. Liao and Z.-Z. Yu, Carbon, 2018, 140, 624–633 CrossRef CAS.
- D. An, S. Cheng, Z. Zhang, C. Jiang, H. Fang, J. Li, Y. Liu and C.-P. Wong, Carbon, 2019, 155, 258–267 CrossRef CAS.
- D. Chen, B. Yang, C. Yang, J. Wu and Q. Zhao, Chin. J. Chem., 2023, 41, 3082–3096 CrossRef CAS.
- L. Jin, W. Cao, P. Wang, N. Song and P. Ding, Nano-Micro Lett., 2022, 14, 133 CrossRef CAS.
- W. Liang, T. Li, X. Zhou, X. Ge, X. Chen, Z. Lin, X. Pang and J. Ge, Nanomaterials, 2020, 10, 544 CrossRef CAS PubMed.
- Y. Chen, X. Hou, M. Liao, W. Dai, Z. Wang, C. Yan, H. Li, C.-T. Lin, N. Jiang and J. Yu, Chem. Eng. J., 2020, 381, 122690 CrossRef CAS.
- P. Gong, L. Li, M. Li, S. Zhang, F. Yang, Y. Wang, X. Kong, H. Chen, C. Jiao, X. Ruan, T. Cai, W. Dai, Z. Pan, Y. Li, L. Xu, C.-T. Lin, N. Jiang and J. Yu, Compos. Commun., 2023, 40, 101596 CrossRef.
- W. Hua, L. Zhang and X. Zhang, J. Mol. Liq., 2021, 340, 117183 CrossRef CAS.
- Y. Xu, X. Wang and Q. Hao, Compos. Commun., 2021, 24, 100617 CrossRef.
- D.-J. Huang, W.-T. Peng, Y.-T. Lee and M.-C. Lu, Int. Commun. Heat Mass Transfer, 2022, 136, 106193 CrossRef CAS.
- H. Waqas, S. A. Khan, U. Farooq, T. Muhammad, A. Alshehri and S. Yasmin, Sci. Rep., 2022, 12, 8035 CrossRef CAS PubMed.
- H. Zhang, X. Zhang, D. Li, J. Zhuang, Y. Liu, H. Liu, D. Wu, J. Feng and J. Sun, Adv. Compos. Hybrid Mater., 2022, 5, 1756–1768 CrossRef CAS.
- J. S. Lewis, T. Perrier, Z. Barani, F. Kargar and A. A. Balandin, Nanotechnology, 2021, 32, 142003 CrossRef CAS.
- Y. Wang, Y. Gao, B. Tang, X. Wu, J. Chen, L. Shan, K. Sun, Y. Zhao, K. Yang, J. Yu and W. Li, RSC Adv., 2021, 11, 25422–25430 RSC.
- W. Dai, X.-J. Ren, Q. Yan, S. Wang, M. Yang, L. Lv, J. Ying, L. Chen, P. Tao, L. Sun, C. Xue, J. Yu, C. Song, K. Nishimura, N. Jiang and C.-T. Lin, Nano-Micro Lett., 2022, 15, 9 CrossRef PubMed.
- Y. Wu, C. Zhang, W. Tu, G. Du, X. Zeng, R. Sun, Y. Xu and L. Ren, Compos. Commun., 2023, 37, 101452 CrossRef.
- Q. Zhang, B. A. Calderon, C. R. Ebbing, L. J. Elston, L. W. Byrd and B.-H. Tsao, Front. Mater., 2020, 7, 572956 CrossRef.
- P. Zhang, J. Zeng, S. Zhai, Y. Xian, D. Yang and Q. Li, Macromol. Mater. Eng., 2017, 302, 1700068 CrossRef.
- D. An, Z. Li, H. Chen, C. Liang, Z. Sun, J. Li, J. Yao, Y. Liu and C. Wong, Composites, Part A, 2022, 156, 106890 CrossRef.
- J. Chen and X. Gao, Diamond Relat. Mater., 2019, 100, 107571 CrossRef CAS.
- J. Zhang, H. Wang, T. Zhang, X. Sun, Y. Meng, C. Ma, T. Zhang, N. Lu, C. Liu and Y. Zeng, Compos. Sci. Technol., 2023, 233, 109915 CrossRef CAS.
- W. Yu, H. Xie, L. Yin, J. Zhao, L. Xia and L. Chen, Int. J. Therm. Sci., 2015, 91, 76–82 CrossRef CAS.
- C.-P. Feng, L.-B. Chen, G.-L. Tian, S.-S. Wan, L. Bai, R.-Y. Bao, Z.-Y. Liu, M.-B. Yang and W. Yang, ACS Appl. Mater. Interfaces, 2019, 11, 18739–18745 CrossRef CAS PubMed.
- W. Dai, T. Ma, Q. Yan, J. Gao, X. Tan, L. Lv, H. Hou, Q. Wei, J. Yu, J. Wu, Y. Yao, S. Du, R. Sun, N. Jiang, Y. Wang, J. Kong, C. Wong, S. Maruyama and C.-T. Lin, ACS Nano, 2019, 13, 11561–11571 CrossRef CAS PubMed.
- S. Sudhindra, L. Ramesh and A. A. Balandin, IEEE Open J. Nanotechnol., 2022, 3, 169–181 Search PubMed.
- J. Pereira da Cunha and P. Eames, Appl. Energy, 2016, 177, 227–238 CrossRef CAS.
- M. Ren, Y. Liu and X. Gao, Energy, 2020, 197, 117262 CrossRef CAS.
- C. Liu, T. Xiao, J. Zhao, Q. Liu, W. Sun, C. Guo, H. M. Ali, X. Chen, Z. Rao and Y. Gu, Renewable Sustainable Energy Rev., 2023, 188, 113814 CrossRef CAS.
- X. Huang, J. Guo, Y. Yang, S. Li, S. Chen, Y. Liu and S. Zhang, J. Appl. Polym. Sci., 2018, 135, 46641 CrossRef.
- N. Alizadeh, R. M. Broughton and M. L. Auad, ACS Appl. Polym. Mater., 2021, 3, 1785–1794 CrossRef CAS.
- J. Jiang, Y. Hong, Q. Li and J. Du, Energy, 2023, 283, 129143 CrossRef.
- W. Lee, J. Hong, J. Song, W. Yang and J. Kim, Compos. Sci. Technol., 2023, 240, 110092 CrossRef CAS.
- M. Emam, S. Ookawara and M. Ahmed, Renewable Energy, 2019, 141, 322–339 CrossRef CAS.
- G. K. S. Khagokpam and S. Halder, High Perform. Polym., 2018, 31, 767–777 CrossRef.
- P. Huang, R. Feng, Z. Tang, Y. He, D. Peng, E. Li, M. Wei, Z. He and Z. Bai, Appl. Therm. Eng., 2023, 235, 121389 CrossRef CAS.
- D. Zou, X. Ma, X. Liu, P. Zheng and Y. Hu, Int. J. Heat Mass Transfer, 2018, 120, 33–41 CrossRef CAS.
- W. Cui, X. Li, X. Li, T. Si, L. Lu, T. Ma and Q. Wang, J. Cleaner Prod., 2022, 367, 133031 CrossRef CAS.
- S. Wu, T. Yan, Z. Kuai and W. Pan, Energy Storage Mater., 2020, 25, 251–295 CrossRef.
- A. Allahbakhsh and M. Arjmand, Carbon, 2019, 148, 441–480 CrossRef CAS.
- J. Yang, G.-Q. Qi, Y. Liu, R.-Y. Bao, Z.-Y. Liu, W. Yang, B.-H. Xie and M.-B. Yang, Carbon, 2016, 100, 693–702 CrossRef.
- A. Hussain, I. H. Abidi, C. Y. Tso, K. C. Chan, Z. Luo and C. Y. H. Chao, Int. J. Therm. Sci., 2018, 124, 23–35 CrossRef CAS.
- J. Ma, W. Du, Z. Chen, W. Wang and L. Zhang, Macromol. Mater. Eng., 2023, 308, 2200332 CrossRef CAS.
- R. Tian, X. Jia, Y. Bai, J. Yang and H. Song, ACS Appl. Mater. Interfaces, 2024, 16, 1451–1460 CrossRef CAS PubMed.
- J. Yang, W. Yu, C. Liu, H. Xie and H. Xu, Compos. Sci. Technol., 2022, 219, 109223 CrossRef CAS.
- P. Win, C.-G. Lin, Y. Long, W. Chen, G. Chen and Y.-F. Song, Chem. Eng. J., 2018, 335, 409–415 CrossRef CAS.
- S. Boon-in, M. Theerasilp and D. Crespy, ACS Appl. Polym. Mater., 2023, 5, 2562–2574 CrossRef CAS.
- J. Yang, W. Yu, Y. Zhang, C. Liu and H. Xie, Int. Commun. Heat Mass Transfer, 2021, 127, 105537 CrossRef CAS.
- S. Cui, F. Jiang, N. Song, L. Shi and P. Ding, ACS Appl. Mater. Interfaces, 2019, 11, 30352–30359 CrossRef CAS PubMed.
- Y. Song, F. Jiang, N. Song, L. Shi and P. Ding, Composites, Part A, 2021, 141, 106222 CrossRef.
- X. Chen, Y. He, M. Tian, L. Qu, T. Fan and J. Miao, Small, 2023, 2308404 Search PubMed.
- J. Lee, H. Yang, C. H. Park, H.-H. Cho, H. Yun and B. J. Kim, Chem. Mater., 2016, 28, 3446–3453 CrossRef CAS.
- H. Wang, L. Wu, L. Xu, L. Zheng, Y. Wu, K. Wu, J. Wang and Q. Chen, Adv. Eng. Mater., 2021, 23, 2001429 CrossRef CAS.
- Q. Ge, J. Chu, W. Cao, F. Yi, Z. Ran, Z. Jin, B. Mao, Z. Li and K. S. Novoselov, Adv. Funct. Mater., 2022, 32, 2205934 CrossRef CAS.
- Y. Guo, C. Dun, J. Xu, J. Mu, P. Li, L. Gu, C. Hou, C. A. Hewitt, Q. Zhang, Y. Li, D. L. Carroll and H. Wang, Small, 2017, 13, 1702645 Search PubMed.
| This journal is © The Royal Society of Chemistry 2025 |