Surface chemical trapping of optical cycling centers

Abstract

Quantum information processors based on trapped atoms utilize laser-induced optical cycling transitions for state preparation and measurement. These transitions consist of an electronic excitation from the ground to an excited state and a decay back to the initial ground state, associated with a photon emission. While this technique has been used primarily with atoms, it has also recently been shown to work for some divalent metal hydroxides (e.g. SrOH) and alkoxides (e.g. SrOCH₃). This extension to molecules is possible because these molecules feature nearly isolated, atomic-like ground and first-excited electronic states centered on the radical metal atom. We theoretically investigate the extension of this idea to a larger scale by growing the alkyl group, R, beyond the initial methyl group, CH₃, while preserving the isolated and highly vertical character of the electronic excitation on the radical metal atom, M. Theory suggests that in the limit as the size of the ligand carbon chain increases, it can be considered a functionalized diamond (or cubic boron nitride) surface. Several requirements must be observed for the cycling centers to function when bound to the surface. First, the surface must have a significant band gap that fully encapsulates both the ground and excited states of the cycling center. Second, while the surface lattice imposes strict limits on the achievable spacing between the SrO– groups, at high coverage, SrO– centers can interact, and show geometric changes and/or electronic state mixing. We show that the coverage of the diamond surface with SrO– cycling centers needs to be significantly sub-monolayer for the functionality of the cycling center to be preserved. Having the lattice-imposed spatial control of SrO– placements will allow nanometer-scale proximity between qubits and will eliminate the need for atom traps for localized cycling emitters. Our results also imply that a functionalization could be done on a scanning microscope tip for local quantum sensing or on photonic structures for optically-mediated quantum information processing.

---

Introduction

Quantum information processing (QIP) is currently in a stage of parallel exploration of multiple platforms. Much like classical electronics, large-scale QIP will require approaches that are amenable to miniaturization and scalability. Along these lines, it seems fitting to approach building a quantum device (sensor, simulator, computer, etc.) by utilizing the natural scale at which quantum effects are important; for electrons at room temperature, this means the energy and size scale of single atoms. In contrast to larger systems that currently dominate the QIP landscape (such as superconducting qubits¹ and phonons in trapped ion Coulomb crystals²), working at the nanometer scale has the potential advantage that inter-qubit coupling can be significantly stronger at short range, leading to systems that require less cooling to access pure collective states. However, single atom engineering at nanometer length scales is most naturally accomplished by chemically bonding the atoms to molecular hosts and using chemical (as opposed to mechanical) assembly. Chemical methods will therefore likely play a major role in development of quantum systems built from single molecular qubits.

Here, we present a new concept for molecular qubits that are designed to be scalable and packed at high density via surface modification, potentially produced by self-assembly of organic molecules. By attaching an optical cycling qubit moiety to a chemically defined crystal surface, we combine initialization and state readout based on optical cycling that trapped atoms provide, with the potential for the nanoscale lithographic control that surfaces furnish. In this way, this “chemically-trapped ion” platform borrows strengths from both gas-phase and solid state devices in an effort to build a concept that can leverage the best features of each for building the next generation of quantum devices.

Surface-bound optical cycling centers

Recent successes in the laser cooling of molecules forms the basis of our design.^3–5 That work demonstrated that many photons can be spontaneously emitted by repeatedly laser-exciting optical transitions from polyatomic molecules without partitioning into excited molecular vibronic states. Common in these systems are ‘functional groups’ based on a metal atom that acts as optical cycling centers (OCCs).⁶ The primary feature of an OCC is an atom-centered optical electronic transition with near-zero Franck–Condon overlap for transitions that change its vibrational state. In this system, successive excitation and spontaneous emission from the OCC can result in a reduction of entropy as the internal state of the molecule is heralded, allowing for quantum state preparation (including laser cooling) and readout. The workhorse of this process is typically alkaline earth metal alkoxide groups (MO-R) in which a radical valence electron centered on the alkaline earth serves as the handle for state preparation and measurement (SPAM).

Our calculations suggest that increasing the size and complexity of the ligands may slightly disrupt the closure of the optical cycle. However the size and complexity effects may be small and can be compensated by additional repumping lasers, if the ligand is spatially and electronically separated from the OCC.⁶ This raises the possibility that an OCC can be chemically tethered to a substrate in vacuo while retaining its ability to spontaneously emit a series of photons upon state-selective excitation, providing readout of the initial internal quantum state of the molecule.

Beyond OCCs’ roles in supplying an isolated transition in the molecule, they also provide a natural basis for storing and using quantum information. A quantum state stored in a pair of long-lived sublevels of the electronic ground state (such as hyperfine structure) serves as a qubit and a state-selective optical cycle would allow excitation of only one of these qubit eigenstates (the “bright state”) for laser-induced fluorescence, while the other eigenstate (the “dark state”) would not emit fluorescence photons. Lack of collected fluorescence therefore constitutes detection (and heralds preparation) of the dark state, while detection of fluorescence indicates the bright state. As such, the optical cycling property allows SPAM of the molecular qubit, in a scheme analogous to those used in trapped ion quantum computers.^7,8

Taken together, the tantalizing possibility that OCCs might be realized on surfaces and even patterned to produce multi-OCC interactions argues for a theoretical treatment of whether molecules hosting optical cycling centers can be attached to surfaces while retaining both chemical and physical properties. We approach this by expanding on the complexity of alkyl chain R-groups that are amenable to optical cycling. For strontium (Sr) as our example of an alkaline earth metal, we suggest that diamond and cubic boron nitride (cBN) may serve as a good substrate for OCC anchoring and derive some general trends. We then explore how multiple OCCs may interact chemically or spectroscopically on a surface. We close by speculating on several schemes by which surface bound OCCs may provide next generation quantum systems through nanoscale control and patterning.

Computational methods

We first probed the electronic structure of the smallest molecular emitters using MRCI/CASSCF (9 electrons/10 orbitals active space) with the def2-TZVPPD basis set.^9–11 The geometries are optimized using the state-average CASSCF method (3 lowest-energy states with weights 0.8/0.1/0.1 for the ground state, and 0.2/0.4/0.4 for the first excited state given its near-degeneracy), and then the MRCI method is used to calculate electronic excitation energies with Molpro.^12–17 These results were used to benchmark the performance of the Density Functional Theory (DFT) and Time-Dependent DFT (TD-DFT) methods,^18–21 implemented in the Gaussian 16 package,²² capable of probing larger molecular systems. We show the comparison between DFT and MRCI/CASSCF for the geometries and excitation energies in Table S1 (ESI†). We found the PBE0 hybrid functional²³ with the D3 dispersion correction²⁴ yielded the most reliable DFT-based results. It is additionally known to work well for excited state calculations.^25–27 We also probed the effects of basis set size and functional (Table S2, ESI†). DFT geometry optimizations are performed with the def2-SVPD basis set, and a larger def2-TZVPPD basis set is used for excitation energy calculations. The effective core potential (ECP) is used for the Sr atom. The Franck–Condon Factors (FCFs) are calculated within the double-harmonic approximation using ezSpectrum.²⁸

Geometry optimizations of OCCs bound to surfaces were performed using the Perdew–Burke–Ernzerhof (PBE) functional,^29,30 with the projector augmented-wave (PAW) potentials,^31,32 implemented in the DFT-based Vienna ab initio simulation package (VASP).^31,33–36 The hybrid functional HSE06³⁷ is used for single point energy calculations, density of states calculations and the Bader charge analysis.^38,39 HSE06 has been extensively benchmarked against other functionals and performs well in predicting band gaps that fall within 1–5 eV.^40,41 A 1 × 1 × 1 Monkhorst–Pack k-point grid centered at Γ-point and a plane-wave cutoff energy of 400 eV are employed, with a convergence criterion of 10⁻⁶ eV for the SCF relaxation. The k-point grid is considered sufficient due to the large size of the unit cell and the significant separation between OCCs that we probe, expected to produce flat bands, accurately modeled with just the Γ-point calculation. A five-layer 2 × 2 supercell with the exposed (111) facet, in periodic boundary conditions, represents the cubic diamond surface as an infinite slab, in which the two surfaces are covered with H atoms. In this supercell 160 C atoms in total, of which 64 are surface-exposed (or 32 per face), all capped with H before SrO deposition. The dimensions of the supercell are 14 Å × 14 Å × 20 Å, which we found to be sufficient to prevent the interaction between the periodic images. The top-three layers of C atoms and the surface H atoms are relaxed during the geometry optimizations. The optimizations are considered converged when the residual forces are less than 0.01 eV per atom.

Results and discussion

Molecular alkoxide radicals

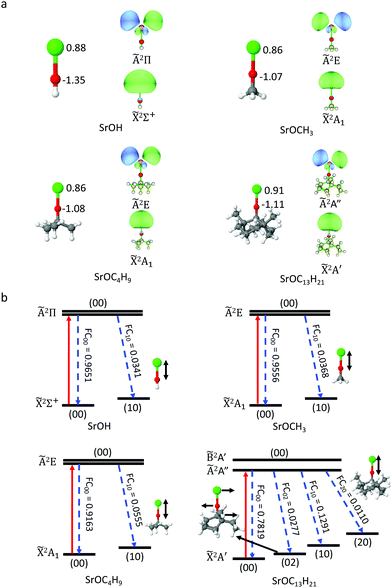
The benchmarking of the computational methodology was done on the SrOH species, for which the experimental data is available, and high-level ab initio theory is affordable. TD-DFT results agree well with the MRCI/CASSCF results and the experiment^42,43 (Tables S1 and S2, ESI†). The TD-DFT optimized Sr–O bond lengths deviate from the experiment values by less than 0.02 Å, and the differences between TD-DFT and CASSCF are less than 0.06 Å. More importantly, for both TD-DFT and CASSCF methods, the computed bond length differences between the ground and excited states differ from the experimental data by 0.002–0.008 Å. All considered functionals give reasonable results for Sr–O bond length and bond length change. The TD-DFT excitation energy agrees with experimental results within 0.1 eV, and the PBE0 hybrid functional performs best in this regard. We also probed the effect of functionals and basis sets. In order to further reduce the computation cost, we use a smaller basis set, def2-SVPD, for geometry optimization and a larger basis set, def2-TZVPPD, for excitation energy calculations. Table S2 (ESI†) shows that this strategy gives a good agreement for bond length change and excitation energy with the results from the def2-TZVPPD basis set. Thus, TD-DFT should provide accurate descriptions for alkoxide radicals. The good performance of DFT is not unexpected, because for optimized OCC the wavefunctions on both electronic states are single configuration and located far from crossings with other electronic states.

We start from the hypothesis that the alkyl group R, in SrOR, can be increased beyond methyl, CH₃. We apply the TD-DFT method to a series of SrOR molecular radicals, R, with increasing numbers of carbon atoms, CH₃, C₄H₉, C₁₃H₂₁ (Fig. 1). Our goal is to progressively build up to the local structure of a diamond surface. We focus on the changes in geometries within the SrO part of the molecular radicals in the ground and first excited states, the excitation energies, and the Frank–Condon factors, FCFs. All the cluster models can maintain a local linear structure, with the Sr–O–C angles of 179.8°–179.9° for the ground state, and 179.6°–180.0° for the excited state. This bond angle is characteristic also of SrOH, and suggests a strongly ionic bond character between Sr and the O atom. As shown in Table 1, the two states in these models are aligned within 0.02–0.03 Å in terms of the equilibrium Sr–O bond length, and larger R sizes correspond to slight deviations from the linear character.

Fig. 1 (a) Optimized ground-state geometries of SrOR. Atomic charges on the Sr and O atoms, computed from NPA, are also shown in the left side of each sub-figure. The right side of each sub-figure shows the NTO for particle orbitals and hole orbitals. The isosurfaces are plotted with an isovalue of 0.03. (b) Photon cycling scheme for SrOR. Excitation from the ground state to the first excited state and spontaneous decay channels are shown with upward red arrows and downward blue dashed arrows. The FCFs are shown along with each decay. The vibrational quantum numbers (v₁v₂) correspond to the Sr–O stretching (v₁) and Sr–O–C bending (v₂) modes.

Table 1 Electronic excitation properties for SrOR. Δr_Sr–O is the Sr–O bond length change from the ground state to the first excited state (Δr_Sr–O = r^ex_Sr–O − r^gs_Sr–O), ΔE is the computed vertical excitation energy, and FCF is the Franck–Condon factor for the decay transition from the first excited state to the ground state. The initial and target states are vibrational ground states

Molecule	ΔrSr–O (Å)	ΔE (eV)	FCF
SrOH	−0.017	1.750	0.9651
SrOCH3	−0.018	1.754	0.9556
SrOC4H9	−0.021	1.738	0.9163
SrOC13H21	−0.029	1.721	0.7819

---

The three cluster models exhibit similar charge distribution on the Sr and O atoms from the natural population analysis (NPA),⁴⁴ due to the similar electron withdrawing strength of the alkoxide groups bound to Sr. The natural transition orbitals (NTOs) in all cluster-bound SrO have the same shape as those in SrOH, with electron density localized on the Sr atom (Fig. 1). This suggests that the perturbation from the R group is minor. However, we observe that, as the cluster size increases, a small amount of electron density appears on the O atom and some on the C atoms, which will make the potential energy surfaces (PESs) of the ground (X̃) and first excited (Ã) states, less parallel, and thus the FCF less diagonal (deviating more form the highly diagonal FCF in SrOH^5,6). This is because more modes are contributing to the off-diagonal FCFs. In addition, the contribution from the Sr–O stretching mode is slightly increased, consistent with our observation that the Sr–O bond length change is increased, and thus the PESs of the two states are less parallel along this mode as we move to larger model systems. However, the decrease in FCF, due to the size effect, is not significant, and SrO will still have a reasonably good FCF. Note as well that the diamond-supported system will have a very different reduced mass.

In SrOC₁₃H₂₁, there is a very small amount of electron density on the two C atoms that are not directly bound to O, but are only 2.7 Å apart from the O atom. These carbon atoms will conform to the top-layer atoms on the diamond surface, which are 2.9 Å away from O in Fig. 2. Consistently, we find that the distance between the O atom and these C atoms changes by 0.004 Å from the X̃²A′ to the òA′′ state, and that constitutes the second largest geometric changes in SrOC₁₃H₂₁. Therefore, when the cycling center is deposited onto the diamond surface, the orbitals of these two C atoms may have weak couplings to the O and Sr atoms and affect the FCF. On the other hand, the chemical nature of these atoms in the diamond surface is not identical to that in a finite hydrocarbon, and thus, this small involvement of the C atoms of the C₁₃H₂₁ system in the key transition does not necessarily preclude the possibility of the infinite surface to be a viable OCC platform.

Fig. 2 (a and b) Optimized geometries of the gas-phase SrOH molecule and the SrO-group bound to the diamond surface. The green, red, gray and white colors represent the Sr, O, C and H atoms, respectively. The atomic charges on Sr and O from the Bader charge analysis are also shown. (c and d) Electron density of the HOMO and LUMO of the SrOH molecule and the SrO supported on diamond. The isosurfaces are plotted with an isovalue of 0.001. (e) PDOS, indicating the excitation energy distance.

The TD-DFT calculations show that the first vertical excitation energy is slightly decreased as the size of the R group increases (Table 1), agreeing well with previous experimental measurements⁴² (Table S3, ESI†). Given this trend, the diamond-bound SrO is expected to have slightly lower excitation energy than SrOH.

Surface functionalization with SrO cycling centers

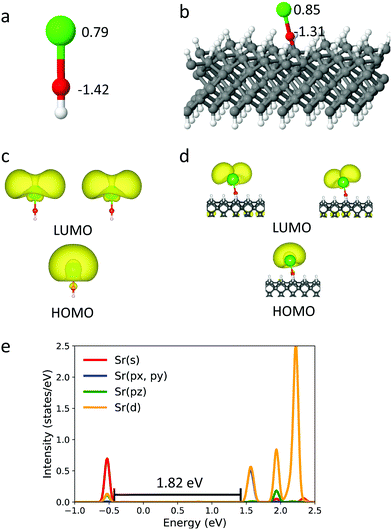
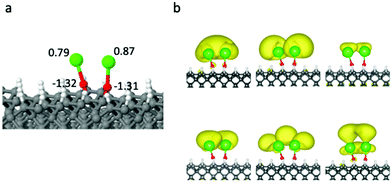
Encouraged by the FCFs observed so far in small clusters, we now expand the R group to encompass the full diamond surface. We first explore the ground state structure of SrO bound to diamond, and compare those to the gas-phase SrOH radical, which is known to have a diagonal FCF. The Sr–Sr separation afforded within this supercell is 14.27 Å. When the SrO group is bound to the surface, the Sr–O–C unit can maintain a roughly linear geometry (Fig. 2), with an angle of 175.2°. The sp³ hybridized C atoms result in a tilted Sr–O–C unit with respect to the surface normal, and the unit thus experiences unbalanced forces from the two sides of the surface, which give rise to the small bend angle. However, this small bending does not affect the extent of density localization on HOMO and LUMO, and will not affect the FCF. The ground-state Sr–O bond length is 2.125 Å on the diamond surface, i.e. 0.019 Å longer than that of the gas-phase SrOH molecule. The atomic Bader charge on Sr within the surface-bound SrO (Fig. 2(a and b)) is +0.85 e, i.e. similar to that in SrOH and nearly identical to those seen in SrOCH₃ and SrOC₄H₉ (Fig. 1), indicating an unpaired electron localized on the cycling center. The overall resemblance of the surface-bound SrO to the best cycling molecules suggests that optical efficient cycling should still be possible at this limit.

Fig. 2(c and d) show the electron density of the highest occupied molecular orbital (HOMO), occupied by the unpaired electron, and the doubly-degenerate lowest unoccupied molecular orbital (LUMO) of the SrOH molecule and the SrO group attached to diamond. For both HOMO and LUMO of surface-bound SrO, a majority of electron density is localized on Sr, leading to electronic transition localized on the cycling center. Again, the molecular orbitals of the surface-bound SrO have similar shapes to those of the SrOH radical, suggesting similar distributions of atomic orbital characters. For SrOH in the X̃²Σ⁺ state, the orbital occupied by the unpaired electron is dominated by the Sr s character with the remaining contribution from the Sr p orbital, whereas for the Ã²Π state, the Sr p and d orbitals dominate the molecular orbital character.

Given the similarity in geometry, charge distribution and shapes of the HOMO and LUMO between the diamond-surface-bound SrO and the SrOH molecule, we expect SrO to maintain its excitation properties once bound to the diamond surface. We can roughly estimate the excitation energy from the projected density of states (PDOS) (Fig. 2e), to be 1.82 eV for diamond-bound SrO. This is close to the excitation energy in SrOH (1.83 eV), estimated from the PDOS calculation. While the number derived from PDOS is necessarily approximate, the HSE06 functional is known to be quite reliable for the optical gap, as discussed above. Calculating the FCF for the infinite surface is unfortunately technically impossible at the moment, and thus, our results are a proposal, substantiated as best as currently possible. Confirming this obviously requires experimental validation.

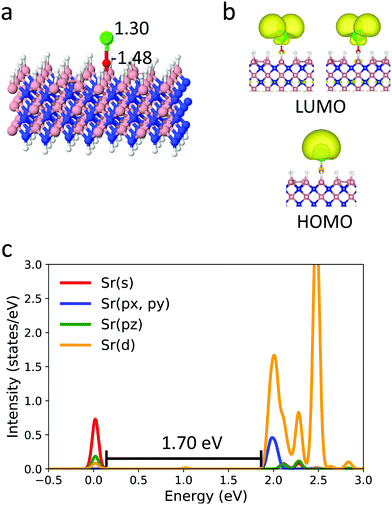
Next, we believe there is a rational way to improve the properties of the surface-bound SrO, through changing the support to a close diamond analogue, cubic boron nitride (cBN). cBN has the same number of valence electrons and the same crystal structure as the cubic diamond, and thus, mirrors diamond's properties. However, it additionally features a small amount of charge transfer between B and N. Given that the surface of cBN is expected to be B-terminated, and that SrO– would therefore bind to the boron, the intra-crystal polarization is expected to effectively create a more electron-withdrawing ligand, R, for SrO–. Fig. 3 shows the optimized structure for SrO–cBN from periodic DFT calculations. The Sr–O bond is 2.104 Å on cBN, i.e. 0.021 Å shorter than that on diamond. The Sr–O–B can maintain a linear structure near Sr, with a now-perfect angle of 180.0°. In line with this finding, and our hypothesis regarding cBN, the Sr atom has more positive charge on cBN than that on diamond. The HOMO and LUMO of this system (Fig. 3) are the expected singly-occupied states, very similar to those of SrO– on diamond and SrOH in the gas phase. From the PDOS, the excitation energy of SrO– on cBN is 1.70 eV. Thus, we see that the behavior of OCC is likely again preserved on cBN at this low coverage. While the experimental confirmation of the OCC behavior on both surfaces is warranted, our results suggest that both diamond and cBN could be used to support the SrO– cycling radical centers, and cBN has a potential to be a superior support.

Fig. 3 (a) Optimized geometry of the SrO– group bound to the boron nitride surface. The green, red, pink, blue and white colors represent the Sr, O, B, N and H atoms, respectively. The atomic charges on Sr and O from the Bader charge analysis are also shown. (b) Electron density of the HOMO and the LUMO of the SrO– supported on cBN. The isosurfaces are plotted with an isovalue of 0.001. (c) PDOS, indicating the excitation energy distance.

Effect of surface coverage

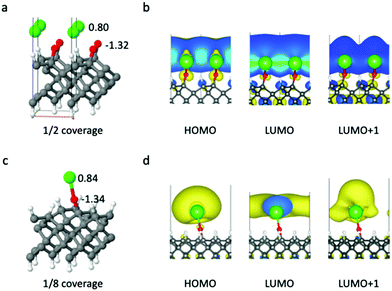
Finally, the interactions and entanglement between the optical cycling centers would be affected by their spatial separation. The surface allows for certain control of it, since the affordable separations are multiples of the surface lattice constant. We explore the effect of surface coverage on the properties of the cycling centers. First, we have studied the interactions between the SrO– groups when they are uniformly distributed on diamond, by changing the size of the periodic supercell. The structure in Fig. 2 corresponds to a coverage of 1/32 monolayer (ML), and it was chosen specifically to avoid the interactions between the Sr centers in the neighboring unit cells. Below we address what happens if coverage increases to 1/8 or even 1/2 ML.

When the cycling center coverage is 1/2 ML, Sr will bind to two O atoms, with bond lengths of 2.33 Å and 2.39 Å, respectively (Fig. 4). The distance between the two Sr centers is 3.57 Å. The HOMO and LUMO are completely delocalized, where the adjacent Sr radical orbitals mix, effectively forming a half-filled σ-band. When the coverage is 1/8 ML, corresponding to the distance between the two cycling centers of 7.13 Å, the Sr–O–C unit can maintain the locally linear structure. However, the orbitals of two neighboring Sr atoms still interact with each other, either polarizing the original orbitals, or mixing and splitting into two mixed states.

Fig. 4 (a and c) Optimized geometries for SrO-diamond with the cycling center coverage of 1/2 and 1/8. Two unit cells are shown for the case of 1/2 coverage. (b and d) Electron density of the HOMO, LUMO, and LUMO+1 for different coverages of cycling centers. The isosurfaces are plotted with an isovalue of 0.001.

We have also studied the systems where two SrO– units are in the same unit cell, and can form dimer geometries. In some cases, one Sr will bind to two O atoms, similar to that in Fig. 4(a), while in other cases the two SrO– groups can maintain the locally linear structures, but their orbitals interact with each other. Fig. 5 shows one case where the distance between two Sr is 3.73 Å, and the distance between the two C atoms that the SrO– groups are bound to is 1.71 Å. The two Sr s orbitals with the same energy form a bonding and an antibonding combinations, while the doubly degenerate p- and d-type orbitals from different Sr form even more mixed orbitals. The charges on the Sr atoms also suggest that they are not chemically identical.

Fig. 5 (a) Optimized geometry for two cycling centers on the diamond surface. The atomic charges on Sr and O from the Bader charge analysis are also shown. (b) Electron density for 6 low energy orbitals. The isosurfaces are plotted with an isovalue of 0.001.

Clearly, these coverages are too high to maintain the clean radical character of the cycling centers in the ground and excited states. Our results indicate that the surface coverage with radical center has to be certainly lower than 1/8 ML, in order for the cycling centers to maintain their local electronic character and the diagonal FCF.

Conclusions and future prospects

In this contribution we showed that the SrO– radical cycling center can be attached to R groups as large as the diamond or cBN surface. Surface patterning with such centers allows for spatial control and alignment. The coverage of the surface with the cycling centers cannot be very high, to prevent their chemical interaction with each other (as seen at 1/2 ML), or mutual electronic perturbation (as seen at 1/8 ML). Even though at 1/8 ML the geometries of the SrO– units are linear, their electronic states can still mix, particularly on the excited state. Furthermore, our results suggest that the surfaces that can successfully host radical cycling centers must feature large band gaps, such that the HOMO and LUMO of the radical are located safely within the gap and not mix with the states of the surface.

We hypothesize that surface supported optical cycling ligands can be realized through chemical functionalization of the surface. We propose that diamond grown by chemical vapor deposition (CVD) (which is typically H-terminated) can be functionalized with pendant hydroxide groups by low-pressure oxygen plasma treatment.^45,46 Following this, reactive Sr can be prepared by exciting the Sr atoms to the metastable state ³P₁ with laser excitation.^47–49 To control the deposition, the amount of pendant hydroxide can be tuned by modulating the power and duration of the plasma treatment.

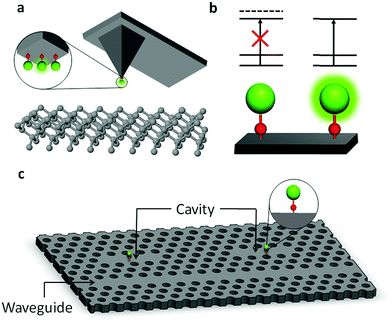
Fig. 6 shows three applications that would be enabled by the development of surface-bound, state-selective emitters. For sensing applications, Fig. 6(a) shows a conceptual arrangement whereby a single molecular qubit could be used for spatial imaging of, for instance, local magnetic fields by functionalizing the tip of a scanning tunneling microscope (STM) or an atomic force microscope (AFM). Light for SPAM can be delivered to and collected from the OCC via fibers or optical waveguides built into the tip. A superposition of field-sensitive qubit states will process at a rate determined by the local magnetic field, and readout after free precession can be used to map the field at the atomic scale.

Fig. 6 Applications of surface bound OCCs. (a) An AFM/STM tip can be functionalized with OCC centers, enabling precision quantum-enhance readout of local magnetic and electric fields through fluorescence. (b) Two OCCs in spatial proximity can provide the two qubit basis for a CNOT gate achieved through dipole blockade. (c) OCCs can be placed in a photonic waveguide, entangling two OCCs via photonic bus.

Note, however, that, if AFM is conducted at ambient pressures, the Sr radicals are likely to chemically react with the gases, and quench. For STM, the tip generates an oriented electric field, which at large enough magnitudes may affect charge separation and hinder Franck–Condon factors. Experimentally, an external electric field generated by STM was shown to stabilize or destabilize charge-transfer in organic molecules placed on gold surfaces, based on alignment. The external electric field strengths studied ranged from −1 × 10⁹ to 1 × 10⁹ V m⁻¹.⁵⁰

To probe how external fields would affect optical cycling, we introduced electrical fields in two ways. A field between −1 × 10¹⁰ to 1 × 10¹⁰ V m⁻¹ aligned with the Sr–O bond was applied to 1/32 ML Sr–O OCCs on diamond (Table S5, ESI†). In another case, a field of 1 × 10⁸–1 × 10¹⁰ V m⁻¹ was applied to two SrO– units located 3.88 Å apart and 10.39 Å from other OCCs on diamond (Table S6, ESI†). In both cases, larger electric fields reduced charge localization on Sr, while the Sr–O bond length would increase or decrease depending on the direction of the field. The effect on charge can be explained by the fact that the field pushes the full electron density in the system, affecting the bonding character on the ground and excited state beyond just the radical-centered HOMO and LUMO. We made a comparison of these results to the cluster model, SrOCH₃, with an external electric field applied along the Sr–O bond. As on the surface, the applied field led to charge delocalization and increase or decrease in Sr–O bond length, depending on the field direction. In both field directions, the ground versus excited state geometry difference increases with increasing field magnitude, implying poorer FCFs (Table S7, ESI†). Thus, in STM, large electric fields can adversely affect radical charge localization and FCF of OCCs.

In Fig. 6(b), two qubits in a quantum processor are shown performing a controlled-NOT (CNOT) quantum gate. Each qubit can be defined on a pair of long-lived internal states |0〉 and |1〉 (for instance, hyperfine levels) that have nearly identical electric dipole moments. Even so, inhomogeneities in the local surface features and attachment details are expected to result in strong (in the sense that they fully mix opposite parity states) static electric fields that are different at each qubit's location, which will lead to small shifts that produce a unique splitting for each qubit. This will allow individual addressing of single-qubit gates through frequency resolution of the applied resonant fields, with the size of the splitting required for resolution set by the available interaction time. State preparation is furnished by laser-driven optical pumping through the OCC.

For two-qubit operations, a third, long-lived state (|0〉) in each molecule that does possess a large electric dipole moment (polarized by the local static field of its environment) can be utilized. Frequency resolution can be used to couple only one of the qubit states of any particular qubit to the auxiliary level, which will Stark shift all of the auxiliary states of the qubits around it via the dipole–dipole interaction (any residual differential shift of the qubit states near the dipole, including the target qubit, can be removed through global dynamical decoupling). In this way, a dipole blockade CNOT gate,⁵¹ between any two qubits within a blockade radius of one another can be performed that does not depend upon their separation. State readout can likewise be performed using frequency-resolved addressing of each molecule's OCC.

Since the proximity of the qubits can be extremely close (but not closer than 1/32 ML on diamond, in our calculations) the energy scale (and therefore achievable speed) of the gate is expected to be high. For example, for 1 Deybe dipoles, the 1 MHz blockade radius could contain about 1000 qubits at 1/32 ML packing. While the coherence properties of these qubits remain an open experimental question, the basic tools presented here show that there is no fundamental impediment to achieving universal quantum computation with this platform.

As a third example, Fig. 6(c) shows a photonic interconnect for large-scale processing based on surface-bound OCCs. Even qubits that are physically distant can interact strongly with one another due to their strong coupling to photonic cavities built from their substrates, and classical routers can turn interactions between individual qubits on and off by optically connecting their photonic cavities together.

We examine the possibility of constructing pendant radical alkaline earth based OCCs on surfaces. Such structures may bridge surface engineering with the precise quantum control afforded by atomic physics. After validating our computational methods, we find that diamond and cBN could support SrO– based OCCs. We establish the necessary density of OCCs on a surface needed to retain independent electronic character and explore how they might be used in applications such as STMs, universal quantum gates, or as substrates for quantum photonics. We believe this presents a path forward to realizing a novel quantum architecture experimentally.

Author contributions

HG, ANA, WC, JRC generated the main project idea. HG and CD performed all calculations. ANA supervised the technical execution of the project. All Authors discussed and analyzed the results. The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Department of Energy Basic Energy Sciences grant DE-SC0019152. This work used computational and storage services associated with the Hoffman2 cluster provided by the UCLA Institute for Digital Research and Education's Research Technology Group, the NSF-supported Extreme Science and Engineering Discovery Environment (XSEDE) (TG-CHE160054).

References

1. P. Krantz, M. Kjaergaard, F. Yan, T. P. Orlando, S. Gustavsson and W. D. Oliver, Appl. Phys. Rev., 2019, 6, 021318.
2. C. D. Bruzewicz, J. Chiaverini, R. McConnell and J. M. Sage, Appl. Phys. Rev., 2019, 6, 021314.
3. E. S. Shuman, J. F. Barry, D. R. Glenn and D. Demille, Phys. Rev. Lett., 2009, 103(22), 223001.
4. M. T. Hummon, M. Yeo, B. K. Stuhl, A. L. Collopy, Y. Xia and J. Ye, Phys. Rev. Lett., 2013, 110(14), 143001.
5. I. Kozyryev, L. Baum, K. Matsuda, B. L. Augenbraun, L. Anderegg, A. P. Sedlack and J. M. Doyle, Phys. Rev. Lett., 2017, 118(17), 173201(6).
6. I. Kozyryev, L. Baum, K. Matsuda and J. M. Doyle, ChemPhysChem, 2016, 17(22), 3641–3648.
7. A. H. Myerson, D. J. Szwer, S. C. Webster, D. T. C. Allcock, M. J. Curtis, G. Imreh, J. A. Sherman, D. N. Stacey, A. M. Steane and D. M. Lucas, Phys. Rev. Lett., 2008, 100(20), 200502.
8. R. Blatt and C. F. Roos, Nat. Phys., 2012, 8(4), 277–284.
9. B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, J. Chem. Inf. Model., 2019, 59(11), 4814–4820.
10. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8(9), 1057–1065.
11. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7(18), 3297–3305.
12. H. J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2(2), 242–253.
13. P. J. Knowles and H. J. Werner, Theor. Chim. Acta, 1992, 84, 95–103.
14. P. J. Knowles and H. J. Werner, Chem. Phys. Lett., 1988, 145(6), 514–522.
15. H. J. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89(9), 5803–5814.
16. H. J. Werner and P. J. Knowles, J. Chem. Phys., 1985, 82(11), 5053–5063.
17. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Gaussian, Inc., Wallingford CT, 2016.
18. J. Liu and W. Liang, J. Chem. Phys., 2011, 135(18), 184111.
19. J. Liu and W. Liang, J. Chem. Phys., 2011, 135(1), 014113.
20. F. Furche and R. Ahlrichs, J. Chem. Phys., 2002, 117(16), 7433–7447.
21. R. Bauernschmitt and R. Ahlrichs, Chem. Phys. Lett., 1996, 256, 454–464.
22. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian, Inc., Wallingford, CT, 2009.
23. J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105(22), 9982–9985.
24. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132(15), 154104.
25. Y. Shao, Y. Mei, D. Sundholm and V. R. I. Kaila, J. Chem. Theory Comput., 2020, 16, 587–600.
26. P. J. Robinson, X. Zhang, T. McQueen, K. H. Bowen and A. N. Alexandrova, J. Phys. Chem. A, 2017, 121(8), 1849–1854.
27. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110(13), 6158–6170.
28. V. A. Mozhayskiy and A. I. Krylov, ezSpectrum, http://iopenshell.usc.edu/downloads.
29. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78(7), 1396.
30. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77(18), 3865–3868.
31. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(3), 1758–1775.
32. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50(24), 17953–17979.
33. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169–11186.
34. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6(1), 15–50.
35. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49(20), 14251–14269.
36. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47(1), 558–561.
37. A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125(22), 224106.
38. W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 7.
39. G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36(3), 354–360.
40. P. Borlido, J. Schmidt, A. W. Huran, F. Tran, M. A. L. Marques and S. Botti, npj Comput. Mater., 2020, 6, 96.
41. P. Borlido, T. Aull, A. W. Huran, F. Tran, M. A. L. Marques and S. Botti, J. Chem. Theory Comput., 2019, 15(9), 5069–5079.
42. C. R. Brazier, L. C. Ellingboe, S. Kinsey-Nielsen and P. F. Bernath, J. Am. Chem. Soc., 1986, 108(9), 2126–2132.
43. S. Yu, J. G. Wang, P. M. Sheridan, M. J. Dick and P. F. Bernath, J. Mol. Spectrosc., 2006, 240(1), 26–31.
44. F. Weinhold and J. E. Carpenter, in The Structure of Small Molecules and Ions, ed. R. Naaman and Z. Vager, Plenum, 1988.
45. H. Notsu, I. Yagi, T. Tatsuma, D. A. Tryk and A. Fujishima, Electrochem. Solid-State Lett., 1999, 2(10), 522–524.
46. H. Kawarada, Surf. Sci. Rep., 1996, 26(7), 205–259.
47. B. L. Augenbraun, J. M. Doyle, T. Zelevinsky and I. Kozyryev, Phys. Rev. X, 2020, 10(3), 31022.
48. W. T. M. L. Fernando, R. S. Ram, L. C. O. O’Brien and P. F. Bernath, J. Phys. Chem., 1991, 95(9), 2665–2668.
49. A. M. R. P. Bopegedera, C. R. Brazier and P. F. Bernath, J. Phys. Chem., 1987, 91(11), 2779–2781.
50. A. C. Aragonès, N. L. Haworth, N. Darwish, S. Ciampi, N. J. Bloomfield, G. G. Wallace, I. Diez-Perez and M. L. Coote, Nature, 2016, 531(7592), 88–91.
51. D. Jaksch, J. I. Cirac, P. Zoller, S. L. Rolston, R. Côté and M. D. Lukin, Phys. Rev. Lett., 2000, 85(10), 2208–2211.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0cp04525j

---