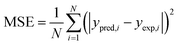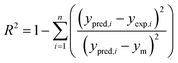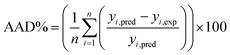DOI:
10.1039/C5RA26036A
(Paper)
RSC Adv., 2016,
6, 19768-19779
Optimization of the process parameters for the adsorption of ternary dyes by Ni doped FeO(OH)-NWs–AC using response surface methodology and an artificial neural network†
Received
7th December 2015
, Accepted 1st February 2016
First published on 2nd February 2016
Abstract
The present study deals with the simultaneous removal of chrysoidine G (CG), rhodamine B (RB) and disulfine blue (DB) by Ni doped ferric oxyhydroxide FeO(OH) nanowires on activated carbon (Ni doped FeO(OH)-NWs–AC). The adsorbent was characterized using X-ray diffraction (XRD), field emission scanning electron microscopy (FE-SEM) and scanning electron microscopy (SEM). Derivative spectrophotometry was used for investigation of simultaneous dye adsorption by an artificial neural network (ANN) and response surface methodology (RSM) to analyse and model their adsorption behavior. Using the ANN analysis, the optimal configuration of the ANN model for modeling of the adsorption process was found to be (6:(4–6):3). The effect of adsorption parameters such as initial pH, adsorbent mass, sonication time and initial CG, RB and DB concentration was studied using central composite design (CCD), while design results were also utilized as a training set for the ANN. After predicting the model using RSM and ANN, the two methodologies were statistically compared by their coefficient of determination, root mean square error, absolute average deviation and mean absolute error based on the validation data set. Results suggest that ANN has better prediction performance as compared to RSM. It was also found that response surface methodology (RSM) predicts the suitability of output parameters. The adsorption mechanism and process rates were investigated by analyzing time dependency data using various conventional kinetic models such as pseudo-first-order and second order, intra-particle diffusion and Elovich models and the best fit was obtained by a pseudo-second-order kinetic model with good agreement between the equilibrium and expected adsorption data. The experimental results revealed that dye adsorption was highly linear and followed the Langmuir isotherm model with maximum adsorption capacities of 187.420 (CG), 210.170 (RB) and 235.650 mg g−1 (DB).
1. Introduction
A great amount of the pollution associated with different aquatic ecosystems is related to dyes,1,2 which are extensively used in the textile industry and other related activities.3 Their wastewater discharge is composed of a high content of dye color, suspended solids and dissolved organics and salts that significantly affect the physicochemical properties of fresh water.4 Some of these dyes are aesthetic pollutants and their presence interferes with light penetration and affects aquatic ecosystems.5 There are many unique and distinguished cleaning procedures for treating the dye-containing wastewater,6 such as biodegradation, coagulation/flocculation, adsorption, chemical oxidation, ozone treatment, membrane filtration, and photocatalysis, but adsorption is the highly preferred technique in view of its effectiveness, high efficiency, economy, simplicity of design and ease of operation. However, good adsorption, regeneration, and isolation characteristics of adsorbents are desirable. Therefore, more research work is required to design new adsorbents with high adsorption capacity, regeneration properties, and easy isolation from an aquatic environment.7
Activated carbon (AC), which is widely applied in industrial processes, has a microporous, homogenous structure with high surface area and radiation stability.8 Furthermore, there are many problems with AC regeneration that can simply be removed by its modification with a nanoscale material that can simultaneously enhance the surface reactive atoms available, as well as its surface area and porosity. Ni doped ferric oxyhydroxide FeO(OH) nanowires, due to their high aspect ratio, high mechanical strength and high surface area, are suitable for efficient adsorption of trace (ppb range) levels of metals and other contaminants. Iron oxide and iron oxyhydroxide particles, particularly the goethite α-FeOOH phase, are environmentally friendly materials which are applicable as adsorbents.
Spectrophotometric methods, despite their convenient properties including simplicity, cost-effectiveness and wide availability in most quality control laboratories, are not selective and sensitive enough for simultaneous quantification of CG, RB and DB. This difficulty is due to the high overlap of their absorption spectra (Fig. 1a), which can be overcome by the application of derivative spectroscopy and derivative ratio spectrophotometry, which simultaneously increase selectivity and sensitivity.9–11
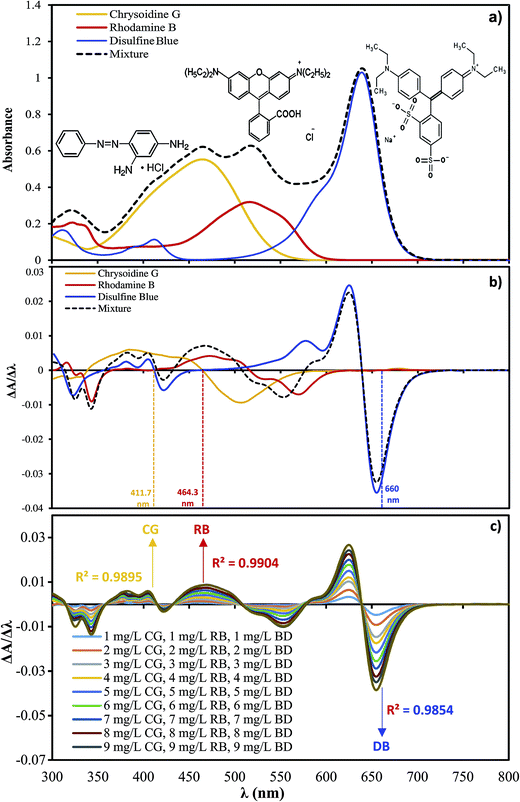 |
| | Fig. 1 (a) Zero order derivative spectra for CG, RB, DB and ternary mixture. (b) First order derivative spectra for CG, RB, DB and ternary mixture. (c) Calibration graph at 411.7 nm for CG, 464.3 for RB and 660 nm for DB. | |
Response surface methodology (RSM) is a powerful technique for testing multiple process variables via a minimum number of experimental trials compared to a “one-factor-at-a-time” method.12,13 In addition, significant interactions among the variables identified and quantified by this technique allows simultaneous optimization of conditions widely performed by Central Composite Design (CCD) or Box–Wilson design.14–17
This work is devoted to the modeling and optimization of the ternary dye adsorption process onto Ni doped FeO(OH)-NWs–AC using derivative spectrophotometry. CCD of the RSM was employed to investigate the effects of significant operating parameters including initial dye concentrations, pH, adsorbent mass and sonication time on dye adsorption to find the most suitable combination of variables to achieve maximum dye adsorption efficiency. The second-order polynomial equation (regression model) provides an excellent explanation of the relationship between the response (R% CG, RB and DB) and independent parameters. This study proposed a three layer ANN model using a back propagation (BP) algorithm to predict adsorption efficiency and subsequently investigate the mechanism kinetics and isotherms.
2. Materials and methods
2.1. Materials
Chemicals including nickel(II) sulfate hexahydrate (NiSO4·6H2O) were provided by the Scharlau. Iron(II) sulfate heptahydrate (FeSO4·7H2O) and ammonium iron(III) sulfate dodecahydrate (NH4Fe(SO4)2·12H2O) were purchased from Sigma. Sulfuric acid (H2SO4), hydrochloric acid (HCl) sodium hydroxide (NaOH) and chrysoidine G (CG, C12H13N4Cl), rhodamine B (RB, C28H31ClN2O3) and disulfine blue (DB, C27H31N2NaO6S2) were purchased from Merck. The adsorption spectra and chemical structures of CG, RB and DB dyes are shown in Fig. 1a. A stock solution (100 mg L−1) of each dye was prepared by dissolving 100 mg of solid dye in 100 mL double distilled/deionized water (Milli-Q, Millipore, Bedford, Massachusetts, USA) and the working concentrations were prepared daily by suitable dilution.
2.2. Instrumental analysis
All of spectrum was recorded by an UV-Vis spectrophotometer (Lambda 25 UV-Vis spectrometer from Perkin-Elmer Instruments, Wellesley, Massachusetts, USA). The concentration of the dyes were calculated at wavelength of 411.7, 464.3 and 660 nm obtained from first order derivative spectra for CG, RB and DB, respectively. The ultrasonic device (TECNO-GAZ, Parma, Italy) was equipped with a digital timer and temperature controller. A pH meter (Ino Lab pH 730, Weilheim, Germany) was used to determine the pH of solutions. A HERMLE bench centrifuge (Hermle-Labortechnik 2206A, Gosheimer Str., Germany) was used to accelerate phase separation. X-ray diffraction (XRD, Philips, PW1800, Eindhoven, Netherlands) was performed to characterize the phase and structure of the prepared nanoparticles using Cu Kα radiation (40 kV and 40 mA) at angles ranging from 20 to 80°. The morphologies of the nanoparticles were observed by scanning electron microscopy and field emission scanning electron microscopy (FE-SEM: Hitachi S-4160, Tokyo, Japan) under an acceleration voltage of 15 kV.
2.3. Ultrasound assisted adsorption experiments
The adsorption of dye solutions onto Ni doped FeO(OH)-NWs–AC was examined using ultrasound as follows: 0.01–0.03 g of Ni doped FeO(OH)-NWs–AC was added into 50 mL of dye solution with a concentration (C0) between 4–50 (mg L−1) at pH 5.0, which was adjusted using 0.1 mol L−1 HCl and/or NaOH, in a glass beaker covered with plastic paraffin film. Then it was mounted on an ultrasound device for 2–6 min at constant temperature (25 °C) to reach equilibrium. Then the sample was immediately centrifuged and effluent solutions were analyzed for the final concentration of CG, RB and DB via derivative spectrophotometric method at 411.7, 464.3 and 660 nm, respectively. The amount of each dye was analyzed via the corresponding calibration curve at the aforementioned wavelength. In ternary solutions, first order derivatives of the absorbance spectra were used to find the optimal wavelength for each dye at which the impact of the other components was minimized. The CG, RB and DB removal percentage (R%) was calculated using the following equation:| |
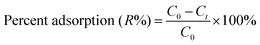 | (1) |
where C0 (mg L−1) and Ct (mg L−1) are the initial dye concentration and after time t, respectively. The amount adsorbed (qe, in mg g−1) is calculated using the following relationship:| |
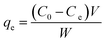 | (2) |
C0 and Ce are the initial and final concentrations (mg L−1) of dye, respectively, V (L) is the volume of the solution and W is the mass of the adsorbent (g).
2.4. Adsorption kinetics
Adsorption kinetic experiments were carried out at various contact times (0.5–8 min) using optimum conditions of other variables. The samples were removed at various time intervals (0.5–8 min) followed by centrifuging and subsequent analysis of the amount of adsorbed dye. Pseudo-first and second order, intra particle diffusion and Elovich models were selected to find an efficient model for the best description of the dye adsorption kinetics.
The adsorption kinetics of dyes was plotted using a pseudo first-order equation:18
| |
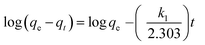 | (3) |
where
qe and
qt are the amount of dye adsorbed (mg g
−1) at equilibrium and at time
t (min),
k1 is the overall rate constant of pseudo-first order adsorption (min
−1). Values of
k1 were calculated from the linear plots of ln(
qe −
qt)
versus t.
The linear form of the pseudo-second order model19 is given by eqn (4):
| |
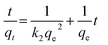 | (4) |
where
qe and
qt are the amounts of dye adsorbed by lignite (mg g
−1) at equilibrium and time
t, respectively, and
k2 is the pseudo second order rate constant (g mg
−1 min
−1).
qe and
k2 can be computed from the slope and intercept of the line from a plot of
t/
qt versus t.
Weber’s intraparticle diffusion model was employed to elucidate the diffusion mechanism and to identify the steps involved in the adsorption process:20
where
Kdif is the intraparticle diffusion rate constant (mg g
−1 h
−1/2), and
c is a constant (mg g
−1) that gives an idea about the thickness of the boundary layer. Weber’s model states that if the passage of the regression line corresponding to
qt versus t1/2 is through the origin, intraparticle diffusion is the only rate-limiting step. Otherwise, two or more steps are involved in the adsorption process.
21,22
Another rate equation based on the adsorption capacity is the Elovich equation, presented as follows:
| |
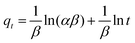 | (6) |
Plot of qt versus ln(t) should yield a linear relationship if the Elovich model is applicable with a slope of (1/β) and an intercept of (1/β)ln(αβ). The Elovich constants are obtained from the slope and the intercept of the straight line.23
2.5. Adsorption isotherms
The adsorption capacity at different aqueous equilibrium concentrations is a measure of how the solutes interact with the adsorbent and assesses the distribution of solute between the solid and liquid phase by measuring the distribution coefficient.24
The linear form of the Langmuir isotherm equation is:
| |
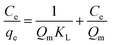 | (7) |
where
qe is the solid phase adsorbate concentration at equilibrium (mg g
−1),
Qm is the maximum adsorption capacity corresponding to complete monolayer coverage on the surface (mg g
−1),
Ce is the concentration of adsorbate at equilibrium (mg L
−1) and
KL is the Langmuir constant (L mg
−1). The constants can be evaluated from the intercepts and slopes of linear plots of
Ce/
qe versus Ce.
25
A linear form of the Freundlich expression can be obtained by taking logarithms of eqn (8):
| |
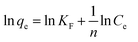 | (8) |
where
qe is the solid phase adsorbate concentration at equilibrium (mg g
−1),
Ce is the equilibrium liquid phase concentration (mg L
−1),
KF the Freundlich constant (L mg
−1) and 1/
n is the heterogeneity factor. Therefore, a plot of ln
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe versus
qe versus ln
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce
Ce enables calculation of
KF and 1/
n.
26
The Temkin isotherm27 assumes that the heat of adsorption of all molecules in the phase decreases linearly when the layer is covered and that the adsorption has a maximum energy distribution of uniform bond.28 The linearized mathematical form of the isotherm is expressed as:
where
B = (
RT)/
b is related to the heat of adsorption,
T is the absolute temperature in Kelvin and
R is the universal gas constant (8.314 J mol
−1 K
−1). Values of
B and
KT were calculated from the plot of
qe against ln
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce
Ce.
29
The Dubinin and Radushkevich (D–R) model was chosen to calculate the apparent free energy of adsorption.30 The linear form of the D–R isotherm equation is described by eqn (10):
| |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe = ln qe = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Q − βε2 Q − βε2
| (10) |
where
qe is the amount of adsorbed dye on the biomass (mol g
−1),
Qs is the maximum biosorption capacity (mol g
−1);
B is the activity coefficient (mol
2 J
−2) corresponding to the mean energy of adsorption and
ε is the Polanyi potential, which is calculated using
eqn (11):
| |
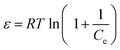 | (11) |
where
R is the gas constant and
T (K) is the absolute temperature. The mean free energy of adsorption (
E) is calculated according to the following relationship:
31| |
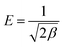 | (12) |
The adsorption process is chemically controlled when the E value falls in the range from 8 to 16 kJ mol−1 and it progresses through a physical mechanism when E is <8 kJ mol−1.
2.6. Preparation of Ni doped FeO(OH)-NWs–AC
The reaction solution for loading Ni doped ferric oxyhydroxide FeO(OH) nanowires (Ni:FeO(OH)-NWs) on activated carbon (AC) was prepared as follows: 0.0190 mmoL NiSO4·6H2O, 0.018 mmol FeSO4·7H2O and 0.021 mmol NH4Fe (SO4)2 were dissolved in 20 mL deionized water with 6 mL H2SO4. Then, deionized water was added to the solution to make a total volume of 150 mL at pH = 2.35. In the next step, 20.0 g AC was added to the prepared solution in an Erlenmeyer flask. Then 240 mL of 2.0 mol L−1 sodium hydroxide was added to the mixture drop-by-drop along with vigorous stirring at room temperature. The obtained solution was stirred at room temperature for 17 h and then the Ni doped FeO(OH)-NWs–AC was filtered and washed several times by distilled water and pre-dried at 40 °C for 1 h and then dried at 70 °C for 7.5 h and finally the prepared Ni doped FeO(OH)-NWs–AC was kept at 35 °C for 15 h and then used as an absorbent for adsorptions experiments.
2.7. Process variables and design of experiments
STATISTICA 10.0 software was applied to generate the matrix and analyze the response surface models. A central composite design (CCD) with 5-levels and 6-factors was selected for this study because it can evaluate quadratic interactions between pairs of factors while minimizing the number of required experiments.32 The influence and interactions of six factors were examined in this study: CG, RB and DB concentration, pH, adsorbent mass and sonication time (Table 1) while their ranges and values were described according to previous studies.33 33 experiments with different factor values were performed. The three responses (R% CG, RB and DB) were measured for each experiment and the synthetic scores were evaluated based on an established mathematic model. The empirical relationships between the three input factors were evaluated from these results. The coded design patterns represent the scaled factor values (lowest (−α), low (−1), central (0), high (+1) and highest (+α)) used in each run for CG, RB and DB concentration, pH, adsorbent mass and sonication time.
Table 1 Experimental factors and levels in the central composite design for the dyes adsorption
| Factors |
Levels |
| Low (−1) |
Central (0) |
High (+1) |
−α |
+α |
| A: CG concentration (mg L−1) |
8 |
12 |
16 |
4 |
20 |
| B: RB concentration (mg L−1) |
8 |
12 |
16 |
4 |
20 |
| C: DB concentration (mg L−1) |
8 |
12 |
16 |
4 |
20 |
| D: pH |
4.0 |
5.0 |
6.0 |
3.0 |
7.0 |
| E: adsorbent mass (g) |
0.015 |
0.020 |
0.025 |
0.010 |
0.030 |
| F: sonication time (min) |
3 |
4 |
5 |
2 |
6 |
| Run |
Factors |
Response |
| A |
B |
C |
D |
E |
F |
R% CG |
R% RB |
R% DB |
| 1 |
12 |
12 |
12 |
3.0 |
0.020 |
4 |
77.84 |
33.69 |
43.25 |
| 2 |
12 |
12 |
12 |
5.0 |
0.020 |
2 |
77.25 |
85.63 |
62.56 |
| 3 |
16 |
16 |
8 |
4.0 |
0.025 |
5 |
75.23 |
63.25 |
50.36 |
| 4 |
8 |
16 |
16 |
4.0 |
0.015 |
3 |
48.27 |
21.88 |
28.63 |
| 5 |
8 |
16 |
16 |
6.0 |
0.025 |
3 |
33.75 |
42.72 |
23.12 |
| 6 |
16 |
8 |
16 |
6.0 |
0.015 |
5 |
71.23 |
79.36 |
48.36 |
| 7 |
8 |
8 |
16 |
4.0 |
0.015 |
5 |
52.08 |
56.96 |
38.56 |
| 8 |
12 |
12 |
12 |
5.0 |
0.030 |
4 |
59.32 |
31.23 |
48.64 |
| 9 |
12 |
12 |
12 |
5.0 |
0.010 |
4 |
21.43 |
70.20 |
19.26 |
| 10 |
12 |
12 |
12 |
5.0 |
0.020 |
4 |
41.20 |
51.20 |
35.86 |
| 11 |
8 |
8 |
16 |
6.0 |
0.025 |
5 |
44.33 |
48.38 |
33.20 |
| 12 |
8 |
8 |
8 |
4.0 |
0.015 |
3 |
63.44 |
23.16 |
51.23 |
| 13 |
12 |
12 |
12 |
5.0 |
0.020 |
4 |
43.89 |
51.06 |
36.89 |
| 14 |
12 |
12 |
4 |
5.0 |
0.020 |
4 |
27.83 |
63.25 |
27.59 |
| 15 |
12 |
12 |
20 |
5.0 |
0.020 |
4 |
44.97 |
41.26 |
32.85 |
| 16 |
12 |
12 |
12 |
5.0 |
0.020 |
4 |
43.20 |
50.95 |
37.86 |
| 17 |
12 |
12 |
12 |
5.0 |
0.020 |
4 |
44.56 |
51.45 |
35.12 |
| 18 |
8 |
16 |
8 |
6.0 |
0.025 |
5 |
78.36 |
71.26 |
65.39 |
| 19 |
16 |
8 |
8 |
4.0 |
0.025 |
3 |
51.70 |
76.52 |
45.36 |
| 20 |
12 |
12 |
12 |
5.0 |
0.020 |
6 |
69.25 |
75.63 |
48.88 |
| 21 |
12 |
20 |
12 |
5.0 |
0.020 |
4 |
13.88 |
52.36 |
12.50 |
| 22 |
12 |
4 |
12 |
5.0 |
0.020 |
4 |
53.85 |
8.12 |
39.46 |
| 23 |
12 |
12 |
12 |
5.0 |
0.020 |
4 |
44.90 |
52.10 |
38.62 |
| 24 |
16 |
8 |
16 |
4.0 |
0.025 |
5 |
66.34 |
71.12 |
48.36 |
| 25 |
16 |
16 |
8 |
6.0 |
0.015 |
5 |
45.76 |
49.63 |
44.69 |
| 26 |
20 |
12 |
12 |
5.0 |
0.020 |
4 |
38.28 |
37.80 |
34.26 |
| 27 |
8 |
8 |
8 |
6.0 |
0.025 |
3 |
38.81 |
42.36 |
20.36 |
| 28 |
12 |
12 |
12 |
7.0 |
0.020 |
4 |
59.88 |
51.20 |
36.52 |
| 29 |
8 |
16 |
8 |
4.0 |
0.015 |
5 |
60.38 |
58.52 |
47.44 |
| 30 |
4 |
12 |
12 |
5.0 |
0.020 |
4 |
79.68 |
68.12 |
63.56 |
| 31 |
16 |
16 |
16 |
6.0 |
0.015 |
3 |
29.63 |
31.25 |
19.52 |
| 32 |
16 |
8 |
8 |
6.0 |
0.015 |
3 |
46.12 |
32.75 |
37.11 |
| 33 |
16 |
16 |
16 |
4.0 |
0.025 |
3 |
62.20 |
65.96 |
46.39 |
The quality-of-fit of the polynomial model was expressed by the coefficient of determination (R2) and statistical significance was checked by an F-test. The residual error, pure error and lack-of-fit were calculated from the repeated measurements.12 The desirability was selected as maximum adsorption of dyes at optimum pH, mass of adsorbent, sonication time and initial concentration of dyes. To visualize the relationship between responses and experimental levels for each of the factors, the fitted polynomial equation was expressed as surface plots.
2.8. Artificial neural networks
Artificial neural networks (ANN) are inspired by the extreme ability of the human brain and nervous systems to learn and classify data.34 ANNs consist of an input and an output layer and one or more hidden layers, while the input and hidden layers have neurons that receive input values. Neurons transfer input values to the next layer and the strength of these connections are determined by their weights.35 In the present study, different back-propagation (BP) algorithms were checked to select the best BP algorithm with a minimum mean squared error (MSE) and best correlation coefficient (R2). The Levenberg–Marquardt back propagation algorithm (LMA) was applied for training of the network as the best algorithm. Also, a three-layer feed forward ANN with a linear transfer function (purelin) at the output layer and a tangent sigmoid transfer function (tansig) at a hidden layer was developed to predict and simulate the adsorption of dyes. For the three dyes, all experimental data (33) were divided randomly into three groups (70%, 15% and 15% of data were applied for training, cross validation and testing of the accuracy of the model and prediction). The training parameters were 6 input nodes, 25 hidden layer neurons, 3 output nodes and error goal: 0.00001. In this study, all inputs and output are normalized within a uniform range of [0, 1] according to the equation below:33,36| |
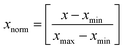 | (13) |
where x is a variable, xmax is the maximum value and xmin the minimum value.
3. Results and discussion
3.1. Characterization of the adsorbent
The morphology and the size of the obtained Ni:FeO(OH) nanowires by FE-SEM (Fig. 2a) reveal its nanowire shape with approximate diameter of 50 nm and length of about 500 nm. The SEM image (Fig. 2b) of the prepared Ni:FeO(OH) nanowires–AC also confirms the presence of its porous structure that effectively increases the surface sites for adsorption.
 |
| | Fig. 2 (a) FESEM image of the α-FeO(OH) nanowires, (b) SEM image of the Ni doped FeO(OH)-NWs–AC and (c) XRD pattern of the prepared α-FeO(OH) nanowires. | |
The structural analysis of the prepared Ni:FeO(OH) nanowires by X-ray diffraction (XRD) (Fig. 2c) confirms XRD peaks at 2θ = 21.3, 34.7, 36.7, 53.1, 59.0 and 61.5° attributed to the lattice planes of (110), (021), (111), (221), (100) and (002), respectively, of the goethite structure of orthorhombic α-FeO(OH)-NWs in good agreement with the reference JCPDS card no. 29-0713. The observed strong XRD peaks (Fig. 2c) indicate the well-crystallized structure of the prepared α-FeO(OH)-NWs while the absence of any characteristic peaks corresponding to impurities, such as Fe, Fe2O3, Fe(OH)2, Fe(OH)3 and/or other compounds, reveals and proves its high purity. The nanocrystal size of the prepared α-FeO(OH) particles was estimated to be about 20 nm based on the Debye–Scherrer formula on the basis of the full width at half-maximum (FWHM) of the (111) peak.37
3.2. Derivative spectrophotometry for simultaneous quantification of CG, RB and DB in ternary systems
The zero-order spectra of dyes exhibit maxima at 461, 543 and 637 nm (Fig. 1a), while the spectrum of their mixture is more complicated with maxima over the range of 400–600 nm. Therefore, direct UV-Vis absorption does not seem suitable for their individual determination in their mixed system. This challenge could be overcome by using the derivative spectrophotometric method based on the theory and applications reported in our pervious works.10,33,38 The first-order derivative absorption spectra of CG, RB and DB in individual and ternary solutions containing 6 mg L−1 of each dye (Fig. 1b) reveal that CG, RB and DB could be determined at 411.7, 464.3 and 660 nm, respectively, where the first-order derivative spectrum of the other dyes is zero. The calibration equations for the three dyes were constructed by plotting the absolute values of the first-order derivative signal (dA/dλ) at 411.7, 464.3 and 660 nm for CG, RB and DB, respectively, against different concentrations of the three dyes (see Fig. 1c). The concentration of each dye could be calculated from their respective calibration graphs under the studied conditions. The amount of each dye was analyzed via the corresponding calibration curve (R2CG = 0.9895, R2RB = 0.0.9904 and R2DB = 0.9854) at the above-mentioned wavelengths.
3.3. Experimental design and quadratic model
The 3-factor CCD matrix and experimental results obtained for the adsorption of the dyes in ternary systems are presented in Table 1. Based on the experimental design (Table 1), the response surface model relating the adsorption efficiency with independent variables was constructed to fit the experimental data. The linear model in terms of coded variables approximated the efficiency of the adsorption process (for R% CG, RB and DB, respectively) as follows:| |
YCG = 248 − 19.5X1 − 0.73X2 + 19.4X3 − 49.4X4 + 113![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200X5 − 83.2X6 − 0.18X1X2 + 0.3X1X3 + 1.8X1X4 + 0.3X1X6 − 0.6X2X3 − 0.4X2X4 + 303.7X2X5 + 2.0X2X6 − 72.0X3X5 − 2.5X3X6 − 2430X4X5 + 4.0X4X6 + 448X5X6 + 0.2X12 − 0.17X22 − 0.14X32 + 6.0X42 − 462 200X5 − 83.2X6 − 0.18X1X2 + 0.3X1X3 + 1.8X1X4 + 0.3X1X6 − 0.6X2X3 − 0.4X2X4 + 303.7X2X5 + 2.0X2X6 − 72.0X3X5 − 2.5X3X6 − 2430X4X5 + 4.0X4X6 + 448X5X6 + 0.2X12 − 0.17X22 − 0.14X32 + 6.0X42 − 462![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300X52 + 7.1X62 300X52 + 7.1X62
| (14) |
| |
YRB = −485 + 16.7X1 + 25.9X2 − 5.2X3 + 122.0X4 + 140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600X5 − 58.8X6 − 0.3X1X2 + 0.2X1X3 − 4.5X1X4 + 343.0X1X5 − 0.8X1X6 − 0.8X2X3 + 0.16X2X4 + 112X2X5 − 1.4X2X6 + 0.2X3X4 − 158X3X5 + 3.2X3X6 − 2823X4X5 + 2.4X4X6 − 1362X5X6 + 0.032X12 − 0.3X22 + 0.021X32 − 2.12X42 + 7.43X62 600X5 − 58.8X6 − 0.3X1X2 + 0.2X1X3 − 4.5X1X4 + 343.0X1X5 − 0.8X1X6 − 0.8X2X3 + 0.16X2X4 + 112X2X5 − 1.4X2X6 + 0.2X3X4 − 158X3X5 + 3.2X3X6 − 2823X4X5 + 2.4X4X6 − 1362X5X6 + 0.032X12 − 0.3X22 + 0.021X32 − 2.12X42 + 7.43X62
| (15) |
| |
YDB = 164.3 − 15.8X1 − 0.9X2 + 14.9X3 − 13.4X4 + 6207X5 − 64.9X6 − 0.2X1X2 + 0.2X1X3 + 1.6X1X4 + 118X1X5 − 0.3X1X6 − 0.63X2X3 + 0.4X2X4 + 228X2X5 + 1.5X2X6 − 0.2X3X4 + 47X3X5 − 1.7X3X6 − 1868X4X5 + 4.9X4X6 + 244X5X6 + 0.2X12 − 0.2X22 − 0.1X32 + 0.8X42 − 271![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500X52 + 4.8X62 500X52 + 4.8X62
| (16) |
where X1, X2, X3, X4, X5 and X6 are the terms of the coded levels for CG, RB and DB concentration, pH, adsorbent mass and sonication time, respectively.
ANOVA was carried out to justify the adequacy of the models. The ANOVA results of the second-order response surface model fitting are given in Table S1† for R% CG, RB and DB. The quality of the constructed model was evaluated based on the coefficient of determination (R2), coefficient of variation (CV%), standard deviation (SD) and also the adequate precision (AP) values. Data given in Table S1† demonstrate that all the models were significant at the 5% confidence level, with their P-values being less than 0.05. The closer the R2 value to unity and the smaller the standard deviation, strongly support a more accurate response being predicted by the model (see Table S2†). The values of the coefficient of determination (R2 = 0.9977, 0.9998 and 0.9984) obtained in the present study for CG, RB and DB removal were higher than 0.80. A good quality of fitting experimental data to a model is indicated by a coefficient of determination of at least 0.80. Fig. 3a shows the correlation of predicted and experimental dye adsorption efficiency. Observed values correspond to experimental data, and predicted values were calculated from the regression equation. It can be seen that there was a consistency between the experimental data and the predicted results. A high R2 value close to 1 demonstrates good agreement between the calculated and observed results within the range of experiments, and shows the presence of desirable and reasonable agreement with adjusted R2. It was shown that the above models were adequate to predict the CG, RB and DB within the studied range of variables.39 The adequate precision (AP) ratio of the models varies as 34.83, 137.4 and 44.22 for CG, RB and DB, which is an adequate signal for the model. AP values higher than 4 are desirable and confirm that predicted models are navigated by the space defined by the CCD.40 The coefficient of variance (CV%) is the ratio of the standard error of the estimate to the mean response value (as a percentage) and identifies the reproducibility of the model. A CV% value less than 10% confirms high reproducibility of experimental data.41 According to Table S2,† the CV% values obtained for all responses studied are relatively small with none of them exceeding 4.0%.
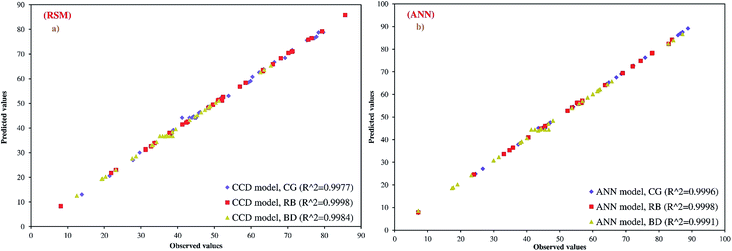 |
| | Fig. 3 The scatter plots of RSM and ANN model predicted values versus actual values for the central composite design matrix. | |
3.4. 2D contour plot analysis
The contour graph (Fig. 4a) displays the variation in removal efficiency based on the increase of initial pH and RB concentration. At low pH values with high proton values, competition between H+ and RB to occupy the reactive sites hinders dye adsorption. On the other hand, simultaneous protonation of dye and adsorbent strongly reduces the attractive force and enhances the repulsive force between them. The adsorbent functional groups like COOH and OH correspond to AC and O and OH correspond to FeO(OH) is protonated. In this study, the removal efficacy increased at higher pH values. This can likely be attributed to the competition between H+ and RB dye being adsorbed on the Ni-FeO(OH)-NWs–AC. At lower pH values, the H+ dye is able to exclude a significant number of adsorption sites at Ni-FeO(OH)-NWs–AC from the RB adsorption process.
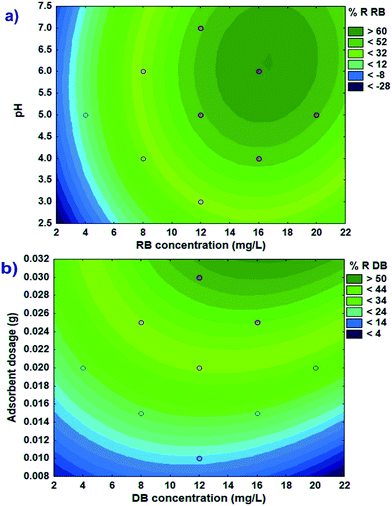 |
| | Fig. 4 Contour plots of combined effects of pH–RB concentration (a) and adsorbent dosage–DB concentration (b) on the % removal of RB and DB, respectively. The actual values of other factors are mean values (coded values 0). | |
The removal efficiency increased with the increase of the adsorbent mass as well as with the increase of the initial DB concentration (Fig. 4b). Increasing the adsorbent dose provided greater surface area and availability of more dye binding sites; hence the rate of dye sorption increased even when the initial dye concentration remained constant. Increasing the initial concentration of the dye increases the probability of contact between dye molecules and Ni-FeO(OH)-NWs–AC particles. However, removal efficiency was observed to decrease slightly when the initial dye concentration and adsorbent mass were increased above some critical values (Fig. 4b). This could be due to the saturation of available binding sites on the adsorbent due to the increased dye concentration. Also, the greater adsorbent dose could create some kind of screening effect hindering the attachment of dye onto binding sites on the dense layer of adsorbent particles.
3.5. Optimization of the dye adsorption
Optimization was carried out to investigate the interaction between the adsorption variables and also to determine the optimum adsorption conditions for optimal removal of CG, RB and DB from aqueous solution using the STATISTICA 10.0 software. According to the software optimization step, the desired goal for each operational condition (CG, RB and DB concentration, pH, adsorbent mass and sonication time) was chosen ‘within the range’. The responses (R% CG, RB and DB) were defined as maxima to achieve the highest performance. The value of desirability obtained (1.0) shows that the estimated function may represent the experimental model and desired conditions. The predicted and experimental results of CG, RB and DB obtained at optimum conditions (Fig. S1†) were obtained using the following conditions: 10 mg L−1 of CG and RB, 8 mg L−1 of DB, pH of 4.0, 0.023 g adsorbent mass and 2 min sonication time, to give experimentally removal of 94.56% CG, 99.60% RB and 74.21% DB. It was observed that the experimental values obtained were in good agreement with the values predicted by the models with relatively small errors (between 0.40% and 0.77% for dye removal). This means that the model can be used to predict the removal efficiencies of dyes under the experimental conditions used.
3.6. Neural network training
The required input–output data for network training were obtained from adsorption experiments and were planned through CCD. The deviations used for selecting the best ANN architecture are the mean square errors (MSE) and absolute fraction of variance (R2) which can be defined as follows:38,42| |
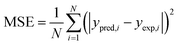 | (17) |
| |
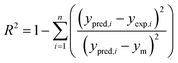 | (18) |
where, N is the number of points, ypred,i is the predicted value obtained from the neural network model, yexp,i is the actual value, and ym is the average of the actual values.
The Levenberg–Marquardt (LMA) algorithm is a standard technique used to solve nonlinear least squares problems. This is one of the most popular methods used in neural network applications because of its relatively high speed, and because it is highly recommended as a first choice supervised algorithm, although it does require more memory than other algorithms. The theory behind and further details of LMA and ANN can be found in the literature.43
Hence, the Levenberg–Marquardt back propagation algorithm (LMA) was applied for the network training as the best algorithm. The optimization of a network is a very important step in network training that is based on optimization of the number of neurons in the hidden layer. For this purpose, different numbers of neurons, in the range of 1–25, were tested in the hidden layer and it was found that hidden layers with 4 for DB, 5 for RB and 6 for CG were the best, permitting achievement of good operation parameters with minimum values of MSE and maximum values of R2 (0.0055 and 0.9997 for CG, 0.0033 and 0.9999 for RB and 0.0046 and 0.9996 for DB, respectively) (Table S3†). As a result, in this study a three layered feed forward back propagation neural network (6:(4–6):3) was used for modeling of the adsorption process.
3.7. Comparison of RSM with ANN
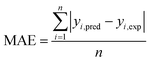
The estimation capabilities of the proposed ANN and RSM techniques for adsorption efficiency of CG, RB and DB were evaluated by means of comparing the responses computed from both methods to the observed data. For this purpose, the techniques were used to predict the responses at 33 experimental points (CCD). The performance of the constructed ANN and RSM models were also statistically measured by the coefficient of determination (R2) (eqn (18)), root mean squared error (RMSE), mean absolute error (MAE) and absolute average deviation (AAD) as follows:33| |
 | (19) |
| |
 | (20) |
| |
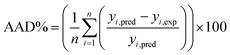 | (21) |
where n is the number of experimental data, yi,pred and yi,exp are the predicted and experimental responses, respectively. R2 measures the percentage of total variation in the response variable that is explained by least-squares regression. R2 must be closed to 1.0, whereas AAD, which is a direct method for describing deviations between predicted and experimental data, must be as small as possible.
Table 2 presents the statistical comparison (i.e. R2, RMSE, AAD and MAE) of RSM and ANN models. Generally, both RSM and ANN models provided good quality predictions in this study and can be considered to perform well in data fitting and offered stable responses. However, the ANN model showed a clear superiority over RSM. This finding is similar to the usual notion that ANN has the best performance compared with RSM.36,44
Table 2 Appraisal of ANN and RSM models
| Models |
Statistical parameters |
| R2 |
MSE |
AAD% |
MAE |
| CG |
RB |
BD |
CG |
RB |
BD |
CG |
RB |
BD |
CG |
RB |
BD |
| ANN |
0.9996 |
0.9998 |
0.9991 |
0.00324 |
0.00325 |
0.00874 |
0.01304 |
0.15830 |
0.73408 |
0.00130 |
0.00208 |
0.00779 |
| RSM (CCD) |
0.9977 |
0.9998 |
0.9984 |
0.79560 |
0.23804 |
0.50359 |
0.2216 |
0.06832 |
0.00901 |
0.85440 |
0.25000 |
0.31560 |
The goodness-of-fit between the experimental and the predicted responses given by the ANN and RSM models is shown in Fig. 3. The distributions of residuals (the difference between predicted and actual values) for both approaches are shown in Fig. S2†. The fluctuations of the residuals are relatively small and regular for ANN compared to RSM. The RSM model shows greater deviation than the ANN model.
However, there is no vagueness in the RSM model compared with the ANN approach, because the RSM model presents all of the relationships between linear, interaction and quadratic effects. Furthermore, the RSM plays an important role in decreasing the number of experiments, cost and time. In addition, RSM optimized the conditions and developed a full quadratic model for the optimum conditions.
3.8. Adsorption kinetics
The results obtained from five kinetic models, including pseudo-first and second order, intraparticle diffusion and Elovich models, at various contact times (0.5–8 min) are given in Table S4.† As can be seen, the pseudo-second order model generated the best fit (R2 > 0.995 for all dyes) of the sorption kinetic data for the three dye-Ni-FeO(OH)-NWs–AC adsorption systems. The theoretical qe(cal) values agree well with the experimental qe(exp) values for all data. This implies that the second order model is in good agreement with experimental data and can be used to favorably explain the dye adsorption on Ni-FeO(OH)-NWs–AC. As shown in Table S4,† the k2 values calculated for RB are higher than the k2 values for CG and DB, suggesting a lower affinity for adsorbent exchange sites.
Using the intraparticle diffusion model, plots of qt (mg g−1) vs. t1/2 were drawn. The applicability of the intraparticle diffusion model requires that the plot passes through the origin, but here the plots for the three dyes do not pass through the origin and so intraparticle diffusion is not the rate controlling step here.
3.9. Equilibrium isotherms
Various isotherm models have been described in order to obtain knowledge about the distribution of adsorbate molecules between the liquid phase and the solid phase before reaching the equilibrium state. The model that best fits the isotherm data is therefore the most suitable model to describe the isotherm behaviour. The Langmuir, Freundlich, Temkin and D–R models were applied to fit the equilibrium data of the dyes onto Ni-FeO(OH)-NWs–AC. According to the presented correlation coefficients in Table 3, the equilibrium data fitted both the Freundlich and Langmuir expressions. However, the high correlation coefficient for the Langmuir isotherm (0.989–0.999) confirmed the applicability of the monolayer sorption model for the dye/Ni-FeO(OH)-NWs–AC systems. In Table 4the values of maximum adsorption capacity (Qmax) and contact time are compared to the values reported for different adsorbents. As can be seen, the present study is superior to previously reported literature in terms of higher adsorption capacity and shorter required time, using a small amount of adsorbent.
Table 3 Isotherm constant parameters and correlation coefficients calculated for the adsorption of dyes onto 0.010 g Ni doped FeO(OH)-NWs–AC in the single component system
| Isotherm |
Parameters |
CG |
RB |
DB |
| Langmuir |
Qm (mg g−1) |
187.42 |
210.17 |
235.65 |
| KL (L mg−1) |
2.33 |
4.66 |
4.55 |
| R2 |
0.989 |
0.997 |
0.999 |
| Freundlich |
1/n |
0.5312 |
0.6625 |
0.7893 |
| KF (L mg−1) |
6.960 |
8.540 |
9.360 |
| R2 |
0.936 |
0.981 |
0.978 |
| Temkin |
B |
17.89 |
25.69 |
29.36 |
| KT (L mg−1) |
22.65 |
39.95 |
45.86 |
| R2 |
0.936 |
0.971 |
0.956 |
| Dubinin–Radushkevich |
Qs (mg g−1) |
69.85 |
98.36 |
100.22 |
| β × 10−7 |
1.00 |
0.312 |
0.324 |
| E (kJ mol−1) |
2.236 |
4.002 |
3.928 |
| R2 |
0.959 |
0.949 |
0.931 |
Table 4 Comparison of the removal of dyes by different methods and adsorbents
| Adsorbent |
Adsorbate |
Sorption capacity (mg g−1) |
Contact time (min) |
Ref. |
| Bottom ash |
CG |
18.08 |
120 |
45 |
| De-oiled soya |
CG |
8.33 |
120 |
45 |
| Row cork |
CG |
57.30 |
50 |
29 |
| CuS-NPs-AC |
CG |
89.30 |
6 |
46 |
| Kaolinite |
RB |
46.08 |
80 |
47 |
| Iron-pillared bentonite |
RB |
98.62 |
40 |
48 |
| Scrap tires |
RB |
280.10 |
500 |
49 |
| Tannic acid functionalized graphene |
RB |
201.00 |
150 |
25 |
| NiO nanoparticles in the presence of H2acacen ligand |
RB |
111.00 |
120 |
30 |
| Zr-containing metal–organic framework formed by terephthalate |
RB |
200.40 |
180 |
50 |
| Ni doped FeO(OH)-NWs–AC |
CG |
187.42 |
2.0 |
This work |
| RB |
210.17 |
| DB |
235.65 |
4. Conclusion
In this study, ANN and RSM have been successfully used to study the modeling, optimization and interaction of the variables for maximum removal percent of ternary dyes using experimental data based upon CCD. RSM was used to determine the major factors influencing CG, RB and DB adsorption efficiency and the interactions between these factors (CG, RB and DB concentration, pH, adsorbent dosage, and sonication time), and to optimize the operating variables as well. Regression analysis showed a good fit of the experimental data to the second-order polynomial model with coefficient of determination values of 0.9977, 0.9998 and 0.9984 for CG, RB and DB, respectively. Under the experimental conditions: 10 mg L−1 of CG and RB, 8 mg L−1 DB, pH 4.0, adsorbent mass 0.023 g and 2 min sonication time, the highest dye adsorption efficiencies were achieved as 94.56%, 99.60% and 74.21% for CG, RB and DB. The removal performance of Ni-FeO(OH)-NWs–AC in the treatment of ternary dye solutions was successfully predicted by applying a three layer neural network with 25 neurons in the hidden layer, and using a back propagation algorithm (LMA). An analysis of the relationship between the predicted results of the designed ANN model and the experimental data was also conducted. The results obtained from the neural model showed that the values of the determination coefficient (R2) were found to be 0.9996 for CG, 0.9998 for RB and 0.9991 for DB. The root mean square error (RMSE), absolute average deviation (AAD), and mean absolute error (MAE) were used together to compare the performance of the RSM and ANN models. The ANN model was found to have higher predictive capability than the RSM model. Based on the findings, the present work indicates that the ANN model is much more accurate in modeling the removal of CG, RB, and DB dyes in comparison to RSM.
The results gained from this study were well described by the Langmuir isotherm model. The kinetic data indicated that the adsorption process was controlled by a pseudo-second-order equation.
Acknowledgements
The authors thanks of the Research Council of the Yasuj University and Social determinates of health research center Yasuj University of medical sciences, Yasuj, Iran for financial supporting this study.
References
- V. K. Gupta, I. Ali, T. A. Saleh, A. Nayak and S. Agarwal, RSC Adv., 2012, 2, 6380–6388 RSC.
- V. Gupta, S. Srivastava, D. Mohan and S. Sharma, Waste Manag., 1997, 17, 517–522 CrossRef CAS.
- L. Liu, Z. Y. Gao, X. P. Su, X. Chen, L. Jiang and J. M. Yao, ACS Sustainable Chem. Eng., 2015, 3, 432–442 CrossRef CAS.
- Q. Liu, B. Yang, L. Zhang and R. Huang, Int. J. Biol. Macromol., 2015, 72, 1129–1135 CrossRef CAS PubMed.
- X. Zhang, H. Yu, H. Yang, Y. Wan, H. Hu, Z. Zhai and J. Qin, J. Colloid Interface Sci., 2015, 437, 277–282 CrossRef CAS PubMed.
- J.-F. Gao, Q. Zhang, K. Su and J.-H. Wang, Bioresour. Technol., 2010, 101, 5793–5801 CrossRef CAS PubMed.
- X. Jin, B. Yu, Z. Chen, J. M. Arocena and R. W. Thring, J. Colloid Interface Sci., 2014, 435, 15–20 CrossRef CAS PubMed.
- U. Gecgel and H. Kolancilar, Nat. Prod. Res., 2012, 26, 659–664 CrossRef CAS PubMed.
- F. N. Azad, M. Ghaedi, K. Dashtian, S. Hajati and V. Pezeshkpour, Ultrason. Sonochem., 2016, 31, 383–393 CrossRef CAS.
- M. Jamshidi, M. Ghaedi, K. Dashtian, A. M. Ghaedi, S. Hajati, A. Goudarzi and E. Alipanahpour, Spectrochim. Acta, Part A, 2016, 153, 257–267 CrossRef CAS PubMed.
- J. Zolgharnein, M. Bagtash and T. Shariatmanesh, Spectrochim. Acta, Part A, 2015, 137, 1016–1028 CrossRef CAS PubMed.
- A. Asfaram, M. Ghaedi, A. Goudarzi and M. Rajabi, Dalton Trans., 2015, 44, 14707–14723 RSC.
- S. Chowdhury, S. Chakraborty and P. D. Saha, Environ. Sci. Pollut. Res., 2013, 20, 1698–1705 CrossRef CAS PubMed.
- P. Das, P. Banerjee and S. Mondal, Environ. Sci. Pollut. Res. Int., 2015, 22, 1318–1328 CrossRef CAS PubMed.
- A. Asfaram, M. Ghaedi, S. Agarwal, I. Tyagi and V. Kumar Gupta, RSC Adv., 2015, 5, 18438–18450 RSC.
- P. F. de Sales, Z. M. Magriotis, M. A. Rossi, R. F. Resende and C. A. Nunes, J. Environ. Manage., 2013, 130, 417–428 CrossRef CAS PubMed.
- M. Dastkhoon, M. Ghaedi, A. Asfaram, A. Goudarzi, S. M. Langroodi, I. Tyagi, S. Agarwal and V. K. Gupta, Sep. Purif. Technol., 2015, 156, 780–788 CrossRef CAS.
- L. Wang, J. Environ. Manage., 2012, 102, 79–87 CrossRef CAS PubMed.
- J. Anandkumar and B. Mandal, J. Hazard. Mater., 2011, 186, 1088–1096 CrossRef CAS PubMed.
- W. J. Weber and J. C. Morris, J. Sanit. Eng. Div., Am. Soc. Civ. Eng., 1963, 89, 53–61 Search PubMed.
- F. Deniz and S. D. Saygideger, Bioresour. Technol., 2010, 101, 5137–5143 CrossRef CAS PubMed.
- K. Kadirvelu, C. Karthika, N. Vennilamani and S. Pattabhi, Chemosphere, 2005, 60, 1009–1017 CrossRef CAS PubMed.
- B. Linhares, C. T. Weber, E. L. Foletto, D. S. Paz, M.A. Mazutti and G. C. Collazzo, Environ. Technol., 2013, 34, 2401–2406 CrossRef CAS PubMed.
- G. L. Dotto, J. M. Santos, I. L. Rodrigues, R. Rosa, F. A. Pavan and E. C. Lima, J. Colloid Interface Sci., 2015, 446, 133–140 CrossRef CAS PubMed.
- K. Liu, H. Li, Y. Wang, X. Gou and Y. Duan, Colloids Surf., A, 2015, 477, 35–41 CrossRef CAS.
- A. Roy, B. Adhikari and S. B. Majumder, Ind. Eng. Chem. Res., 2013, 52, 6502–6512 CrossRef CAS.
- M. Temkin and V. Pyzhev, Acta Physicochim. URSS, 1940, 12, 217–222 Search PubMed.
- E. L. Foletto, C. T. Weber, D. S. Paz, M. A. Mazutti, L. Meili, M. M. Bassaco and G. C. Collazzo, Water Sci. Technol., 2013, 67, 201–209 CrossRef CAS PubMed.
- V. M. Nurchi, M. Crespo-Alonso, R. Biesuz, G. Alberti, M. I. Pilo, N. Spano and G. Sanna, Arabian J. Chem., 2014, 7, 133–138 CrossRef CAS.
- F. Motahari, M. R. Mozdianfard and M. Salavati-Niasari, Process Saf. Environ. Prot., 2015, 93, 282–292 CrossRef CAS.
- S. Kaur, S. Rani, R. K. Mahajan, M. Asif and V. K. Gupta, J. Ind. Eng. Chem., 2015, 22, 19–27 CrossRef CAS.
- F. Nasiri Azad, M. Ghaedi, K. Dashtian, S. Hajati, A. Goudarzi and M. Jamshidi, New J. Chem., 2015, 39, 7998–8005 RSC.
- A. Asfaram, M. Ghaedi, S. Hajati and A. Goudarzi, RSC Adv., 2015, 5, 72300–72320 RSC.
- M. Ghaedi, A. M. Ghaedi, A. Ansari, F. Mohammadi and A. Vafaei, Spectrochim. Acta, Part A, 2014, 132, 639–654 CrossRef CAS PubMed.
- T. Shojaeimehr, F. Rahimpour, M. A. Khadivi and M. Sadeghi, J. Ind. Eng. Chem., 2014, 20, 870–880 CrossRef CAS.
- E. A. Dil, M. Ghaedi, A. M. Ghaedi, A. Asfaram, A. Goudarzi, S. Hajati, M. Soylak, S. Agarwal and V. K. Gupta, J. Ind. Eng. Chem., 2016, 34, 186–197 CrossRef CAS.
- A. Goudarzi, G. M. Aval, R. Sahraei and H. Ahmadpoor, Thin Solid Films, 2008, 516, 4953–4957 CrossRef CAS.
- M. Ghaedi, S. Hajati, M. Zare, M. Zare and S. Y. Shajaripour Jaberi, RSC Adv., 2015, 5, 38939–38947 RSC.
- H. Mazaheri, M. Ghaedi, S. Hajati, K. Dashtian and M. K. Purkait, RSC Adv., 2015, 5, 83427–83435 RSC.
- M. Ghaedi, H. Z. Khafri, A. Asfaram and A. Goudarzi, Spectrochim. Acta, Part A, 2016, 152, 233–240 CrossRef CAS PubMed.
- A. Asfaram, M. Ghaedi, A. Goudarzi, M. Soylak and S. Mehdizadeh Langroodi, New J. Chem., 2015, 39, 9813–9823 RSC.
- H. Karimi and M. Ghaedi, J. Ind. Eng. Chem., 2014, 20, 2471–2476 CrossRef CAS.
- A. Bouchachia, Adaptive and Intelligent Systems: Third International Conference, ICAIS 2014, September 8–9, 2014, Proceedings, Springer, Bournemouth, UK, 2014 Search PubMed.
- B. Hameed, J. Hazard. Mater., 2009, 161, 753–759 CrossRef CAS PubMed.
- A. Mittal, J. Mittal, A. Malviya and V. K. Gupta, J. Colloid Interface Sci., 2010, 344, 497–507 CrossRef CAS PubMed.
- A. R. Bagheri, M. Ghaedi, S. Hajati, A. M. Ghaedi, A. Goudarzi and A. Asfaram, RSC Adv., 2015, 5, 59335–59343 RSC.
- T. A. Khan, S. Dahiya and I. Ali, Appl. Clay Sci., 2012, 69, 58–66 CrossRef CAS.
- M.-F. Hou, C.-X. Ma, W.-D. Zhang, X.-Y. Tang, Y.-N. Fan and H.-F. Wan, J. Hazard. Mater., 2011, 186, 1118–1123 CrossRef CAS PubMed.
- L. Li, S. Liu and T. Zhu, J. Environ. Sci., 2010, 22, 1273–1280 CrossRef CAS.
- Q. He, Q. Chen, M. Lü and X. Liu, Chin. J. Chem. Eng., 2014, 22, 1285–1290 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c5ra26036a |
|
| This journal is © The Royal Society of Chemistry 2016 |
Click here to see how this site uses Cookies. View our privacy policy here. 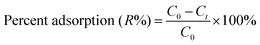
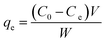
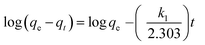
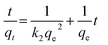
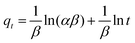
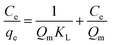
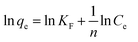
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe versus ln
qe versus ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce enables calculation of KF and 1/n.26
Ce enables calculation of KF and 1/n.26
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KT + B
KT + B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce
Ce
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ce.29
Ce.29
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) qe = ln
qe = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Q − βε2
Q − βε2
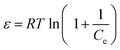
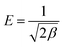
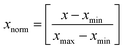

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 200X5 − 83.2X6 − 0.18X1X2 + 0.3X1X3 + 1.8X1X4 + 0.3X1X6 − 0.6X2X3 − 0.4X2X4 + 303.7X2X5 + 2.0X2X6 − 72.0X3X5 − 2.5X3X6 − 2430X4X5 + 4.0X4X6 + 448X5X6 + 0.2X12 − 0.17X22 − 0.14X32 + 6.0X42 − 462
200X5 − 83.2X6 − 0.18X1X2 + 0.3X1X3 + 1.8X1X4 + 0.3X1X6 − 0.6X2X3 − 0.4X2X4 + 303.7X2X5 + 2.0X2X6 − 72.0X3X5 − 2.5X3X6 − 2430X4X5 + 4.0X4X6 + 448X5X6 + 0.2X12 − 0.17X22 − 0.14X32 + 6.0X42 − 462![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300X52 + 7.1X62
300X52 + 7.1X62
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600X5 − 58.8X6 − 0.3X1X2 + 0.2X1X3 − 4.5X1X4 + 343.0X1X5 − 0.8X1X6 − 0.8X2X3 + 0.16X2X4 + 112X2X5 − 1.4X2X6 + 0.2X3X4 − 158X3X5 + 3.2X3X6 − 2823X4X5 + 2.4X4X6 − 1362X5X6 + 0.032X12 − 0.3X22 + 0.021X32 − 2.12X42 + 7.43X62
600X5 − 58.8X6 − 0.3X1X2 + 0.2X1X3 − 4.5X1X4 + 343.0X1X5 − 0.8X1X6 − 0.8X2X3 + 0.16X2X4 + 112X2X5 − 1.4X2X6 + 0.2X3X4 − 158X3X5 + 3.2X3X6 − 2823X4X5 + 2.4X4X6 − 1362X5X6 + 0.032X12 − 0.3X22 + 0.021X32 − 2.12X42 + 7.43X62
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500X52 + 4.8X62
500X52 + 4.8X62