Open Access Article
Open Access ArticleCation distribution: a descriptor for hydrogen evolution electrocatalysis on transition-metal spinels†
Aya K.
Gomaa‡
 a,
Maram G.
Zonkol‡
a,
Ghada E.
Khedr
a,
Maram G.
Zonkol‡
a,
Ghada E.
Khedr
 b and
Nageh K.
Allam
b and
Nageh K.
Allam
 *a
*a
aEnergy Materials Laboratory, School of Sciences & Engineering, The American University in Cairo, Cairo, 11835, Egypt. E-mail: nageh.allam@aucegypt.edu
bDepartment of Analysis and Evaluation, Egyptian Petroleum Research Institute, Cairo, 11727, Egypt
First published on 6th August 2024
Abstract
Exploring cost-effective and efficient electrocatalysts for the hydrogen evolution reaction (HER) is essential for realizing green energy technologies such as water electrolyzers and fuel cells. To this end, identifying descriptors that determine the activity of the employed catalysts would render the process more efficient and help to design selective catalytic materials. Herein, cation distribution (δ) is presented as the activity descriptor for the HER on CoFe2O4 spinels. A one-step hydrothermal synthesis method is demonstrated for the fabrication of flower-shaped spinel CoFe2O4 nanosheets on Ni foam at various pH values with different cation distributions. XPS and Raman analyses revealed the cation distribution of Co and Fe as the main factor determining the catalytic activity of the material. This has been confirmed both experimentally and computationally. The catalyst with the largest δ (0.33) showed as low as 66 mV overpotential at −10 mA cm−2 with exceptional stability for 44 hours of continuous electrolysis in 1 M KOH. Our study demonstrates cation distribution in spinels as a descriptor of their HER catalytic activity.
Broader contextExploring efficient and low-cost electrocatalysts for the hydrogen evolution reaction (HER) and oxygen-evolution reaction (OER) is critical for developing renewable energy technologies such as fuel cells, metal–air batteries, and water electrolyzers. The rational design of a catalyst can be guided by identifying descriptors that determine its activity. This is a descriptor study of the HER of spinel oxides, which enables the design and fabrication of exceptionally active HER electrocatalysts. A general principle is that the ratio of the occupancy of the active cation in the tetrahedral and octahedral sites is the activity descriptor for the HER of spinels. This study may possibly inspire more insightful studies on the catalysis of water splitting among other electrochemical processes. |
Introduction
Access to affordable, clean, and reliable energy is crucial for economic growth and global prosperity. This becomes even more pronounced as the currently existing non-renewable energy sources are becoming scarce owing to fossil fuel depletion and the alarming increase in carbon dioxide emissions.1,2 In this regard, hydrogen (H2) is not only a vital raw material in the chemical industry but also plays an immense role in the future energy landscape. It serves as a zero-carbon energy carrier and can be directly used as a fuel in hydrogen fuel cells, leaving behind only water as a byproduct. Additionally, hydrogen boasts the highest specific energy among conventional fuels, with a high energy yield of 122 kJ g−1, making it an attractive alternative to fossil fuels.3 Electrocatalytic water splitting, which involves the oxygen evolution reaction (OER) and the hydrogen evolution reaction (HER), has garnered global attention in recent years as a propitious process for large-scale hydrogen production.4,5 Nonetheless, the thermodynamic and kinetic challenges associated with the OER and HER hinder the efficiency of water electrolysis. The high electrode overpotential required for initiating overall water splitting reduces the overall efficiency, leading to high-energy consumption. Therefore, developing durable active electrocatalysts is essential to overcome the sluggish kinetics of the two half-reactions and to accelerate their reaction rates.6,7 Traditionally, platinum, ruthenium, and iridium-based materials have been considered the most effective catalysts for the HER and OER. However, their scarcity and high cost limit their widespread use. As a result, recent focus has been shifted towards earth-abundant metal oxides, sulfides, phosphides, nitrides and chalcogenides that exhibit comparable activity to precious-metal-based catalysts.8–13However, discovering efficient electrocatalysts remains a challenge due to the vast materials space and difficulty and expense in identifying the appropriate catalytic materials. Therefore, there is an urgent need to identify efficient methods for understanding the HER mechanism and screening different electrocatalysts. By doing so, the progress in developing efficient and cost-effective electrocatalysts for water splitting can be accelerated, thus enabling the ubiquitous adoption of hydrogen as a clean and sustainable energy source.14,15 In catalysis, descriptors derived from the simulations and experiments establish a link between the intrinsic activity of the electrocatalysts and their physicochemical characteristics during electrochemical reactions. Thus, descriptors have been considered as a tool for predicting the catalytic activity (ECA) of electrocatalysts.16,17 For different reactions and different classes of materials there are many descriptors that are used to demonstrate the different catalytic activities and how to control the reaction rate and reaction mechanism via tuning the structure or controlling the activity descriptors.18 Controlling these descriptors would imply understanding the relationship between the catalyst, the reactants, and the intermediates. For the HER, the adsorption energy (ΔG) is one of the universal descriptors. The smaller the energy difference between the experimental ΔG and the optimum value (ΔG° ∼ 0 eV), the superior the catalytic activity, as indicated by Sabatier's law.19 Another important descriptor in catalysis, particularly for transition metals, is the d-band center. The adsorption energy of intermediates is sensitive to the shift of the d-band center toward the Fermi level, which significantly and potentially alters the reaction pathway and the energy barriers of the rate-determining step, ultimately affecting the reaction kinetics of the catalytic process.18–21 Additionally, tuning these descriptors within a specific class of materials directly affects their chemical and physical properties.
Among the various electrocatalytic materials, spinel ferrites possess an essential parameter that directly affects their physical, chemical, and catalytic properties, i.e., cation distribution (δ).22–24 The general formula of spinel ferrites is (MδFe1−δ)[M1−δFe1+δ]O4, where the parentheses denote the tetrahedral sites and the square brackets represent the octahedral sites25 and δ is the inversion parameter quantifying the distribution of M2+ and Fe3+ cations among these sites. The tetrahedral sites are located at the corners of the unit cell and are coordinated to four oxygen atoms. In comparison, the octahedral sites are situated in the center of the unit cell faces and are coordinated to six oxygen atoms. The inversion parameter (δ) is usually used to quantify the distribution of the cations among the tetrahedral and octahedral sites. In particular, the choice of spinel ferrites for electrocatalytic applications arises from their distinguishable properties such as electrochemical durability under harsh conditions and the ability to control and tune their redox features via modulation of the divalent ion in accordance with the respective application.26,27
Of specific interest, spinel cobalt ferrite (CoFe2O4) has received special attention in the field of electrocatalysts due to its excellent electrochemical stability, magnetic, and electronic properties.28–30 However, CoFe2O4 still has some drawbacks such as low conductivity and a slow ion diffusion rate. In this regard, the reaction conditions, including temperature, pH, and time, used for the growth of CoFe2O4 have a great impact on the morphology, surface area, cation distribution, and chemical and physical characteristics of the material,31 which directly influence the performance of the electrocatalyst. For example, the octahedral sites in spinels are usually more catalytically active than the tetrahedral sites.32–34 Therefore, the relative distribution of particular cations in these sites might change their catalytic activity.35 Accordingly, it is indispensable to optimize the exact conditions that result in a catalyst with the highest electrocatalytic activity toward the HER. Specifically, to ensure high catalytic activity and fast electron transport, the catalyst must be loaded on a conductive substrate. The 3D porous architecture of the conductive nickel foam (NF) is beneficial for increasing the active sites.36 The high surface area-to-volume ratio of the foam also enables efficient mass transfer of reactants and products, leading to improved reaction kinetics and significantly enhancing the performance of electrochemical and catalytic reactions.37
Herein, we demonstrate the possibility of using cation distribution in spinels as a descriptor of their HER electrocatalytic activity. To better visualize the effect of cation distribution on the electrocatalytic activity, CoFe2O4 supported on NF was fabricated via a simple, yet optimized, one-step hydrothermal route. The use of NF as a substrate and optimizing the solution pH enable the fabrication of the material with different cation distributions. The electrocatalytic activity of the resulting materials was elucidated towards the HER, revealing a direct correlation between the cation distribution and the activity of the material. Of specific interest, the CoFe2O4 catalyst prepared at pH 9 showed an outstanding low overpotential of 66 mV at −10 mA cm−2 towards the HER with high stability over 44 h of continuous electrolysis in 1 M KOH. These findings were also confirmed by density functional theory (DFT) calculations, unveiling the effect of different cation distributions on the catalytic behavior and the underlying reaction mechanisms.38–40 We hope this work opens a new avenue for considering cation distribution (δ) as an activity descriptor for other catalytic systems to help better design efficient electrocatalysts for a plethora of applications.
Experimental section
Materials
The following materials were purchased and used with no further purification: cobalt nitrate hexahydrate (Co(NO3)2·6H2O, Alfa Aesar, ThermoFisher, Germany), Ni foam (Goodfellow, UK), ferrous nitrate nonahydrate ((Fe(NO3)3·9H2O); Techno Pharmchem, India), sodium hydroxide (NaOH; Panreac, Spain), absolute ethanol (Sigma Aldrich), and distilled water.Synthesis of CoFe2O4/Ni foam
First, Ni foam was cleaned with absolute ethanol for 10 min in a sonication bath, followed by washing with distilled water for another 10 min and drying at 60 °C for 15 min. Next, a mixed solution was formed by adding 5.7 g of (Fe(NO3)3·9H2O) to 2.04 g of (Co(NO3)2·6H2O) in 50 mL of distilled water and stirring until fully dissolved. In a separate beaker, 2.65 g of NaOH pellets were added to 60 mL of distilled water and stirred until fully dissolved. The NaOH solution was then dropwise added to the mixed solution with continuous stirring until the pH reached the desired value (9, 12.5, and 13). 5 mL of this solution was then added to 45 mL of distilled water under stirring. The mixture was then poured into an 80 mL Teflon reactor. The previously prepared Ni foam was added to the mixture, and the whole system was heated to 180 °C for 24 h before being allowed to cool naturally to ambient temperature. After cooling, the sample was washed with deionized water via sonication and then dried in a drying oven at 60 °C for 1 h. The resulting material is CoFe2O4/Ni foam as depicted in Scheme 1.Characterization of materials
Zeiss Ultra 60 FESEM equipment was utilized to elucidate the morphology. The vibration modes present in the samples were identified using Fourier transform infrared spectroscopy (FTIR, Thermo Scientific Nicolet) in the range of 400–4000 cm−1. A Rigaku SmartLab X-ray diffractometer was employed to identify the crystal structure of the films at a step rate of 0.007°. An ESCALAB 250Xi X-ray photoelectron spectrometer (Thermo Scientific) was used to elucidate the surface composition with the C 1s signal at 284.8 eV as the reference. Transmission electron microscopy (TEM) (Thermo Scientific, Talos F200i) was utilized to examine the morphology and crystal structure via the selected area electron diffraction (SAED) pattern. A 12 mW laser power-Bruker Raman microscope was employed to record the Raman spectra at λexcitation = 785 nm.Electrochemical characterization
The electrochemical scans were conducted using an SP300 Biologic potentiostat. The samples (bare Ni foam and CoFe2O4/Ni foam, 1 cm2 each), graphite rod, and 1 M KOH were used as the working electrode, counter electrode, and electrolyte for the HER measurements in a 3-electrode cell with Hg/HgO as the reference electrode. The potentials were expressed on the reversible hydrogen electrode (RHE) scale using eqn (1):| V(Hg/HgO) = V(RHE) − (0.098 + 0.059 pH) | (1) |
| η = E(HER in RHE scale at 10 mA) − 0 V | (2) |
| Ic = vCDL | (3) |
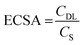 | (4) |
The electrochemical impedance spectroscopy (EIS) scans were recorded at −0.176 V (RHE) in the frequency range (1 mHz–100 KHz) to estimate the charge transfer and solution resistances. Moreover, chronopotentiometry (CP) scan was carried out at −15 mA cm−2 for 44 h to elucidate the stability of the catalysts. In all HER measurements, ohmic drop (iR) of the half-cell reaction was compensated to account for the electrolyte resistance. The electrochemical performance of the entire system was assessed from the recorded LSV plots in the potential window of 1–2 V at a scan rate of 10 mV s−1. Also, the CP test for 48 h at 15 mA cm−2 was used to elucidate the stability of the catalyst. The faradaic efficiency (FE) was estimated using an H-cell via the water displacement method with RuO2 as a counter electrode in 1 M KOH as an electrolyte. The measurements were done via CP at 20 mA cm−2 for 1 h. The detailed calculations of the FE are listed in the ESI.†
Computational details
The Vienna Ab initio Simulation Package (VASP 5.4.4) was used for all calculations. The interactions among the valence and the core electrons and the exchange–correlation potential were described using the generalized gradient approximation (GGA) with Perdew–Burke–Ernzerhof (PBE) and projected augmented wave (PAW) functionals using a conjugate-gradient algorithm. A cut-off energy of 600 eV was used to reach convergence within 10−8 eV and a 1 × 2 × 2 Monkhorst–Pack K-point mesh was used. For charge and density of state analyses, a 10 × 10 × 10 Monkhorst–Pack K-point mesh was applied. We started with the normal spinel structure (Fe16Co8O32) with the Fd3m space group from the Materials Project database, then a supercell of 2 × 1 × 1 was constructed, then we modelled three structures, the ideal inverse spinel structure having only Fe in the tetrahedron and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 Co
1 Co![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fe in the octahedron, distorted inverse spinel structure having 0.25
Fe in the octahedron, distorted inverse spinel structure having 0.25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.75 Co
0.75 Co![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fe and 0.75
Fe and 0.75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.25 Co
1.25 Co![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fe and distorted inverse spinel structure having 0.32
Fe and distorted inverse spinel structure having 0.32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.68 Co
0.68 Co![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fe and 0.68
Fe and 0.68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.32 Co
1.32 Co![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fe, and then we did geometry optimization. After the bulk optimization, the (3 1 1) surface was cleaved with a vacuum slab of 15 Å in the c-direction to prevent interactions between images. The 311 plane was chosen as it showed the most dominant peak, see Fig. S1 (ESI†). Also, we simulated Ni foam by starting with cubic Ni of space group Fm3m and then a supercell of 2 × 2 × 2 was created and a (1 1 1) slab was designed. To simulate the effect of Ni foam, a two-layer slab from Ni foam (bottom layer) and a distorted inverse spinel Fe2CoO4 (CFOdis) (top layer) were created. All the surfaces were fully relaxed using a k-point mesh of 3 × 3 × 1.
Fe, and then we did geometry optimization. After the bulk optimization, the (3 1 1) surface was cleaved with a vacuum slab of 15 Å in the c-direction to prevent interactions between images. The 311 plane was chosen as it showed the most dominant peak, see Fig. S1 (ESI†). Also, we simulated Ni foam by starting with cubic Ni of space group Fm3m and then a supercell of 2 × 2 × 2 was created and a (1 1 1) slab was designed. To simulate the effect of Ni foam, a two-layer slab from Ni foam (bottom layer) and a distorted inverse spinel Fe2CoO4 (CFOdis) (top layer) were created. All the surfaces were fully relaxed using a k-point mesh of 3 × 3 × 1.
Results and discussion
Fig. 1 illustrates the FESEM images of the as-grown cobalt ferrite on Ni foam at different pH values. Fig. 1(a) reveals the formation of flower-like nanosheets at pH 9, with enormous surface area and a large number of active sites suitable for redox reactions and electrocatalysis.42 Upon changing the pH to 12.5 and 13, the morphology is changed into nanoneedles (Fig. 1(b)) and prism structure (Fig. 1(c)), respectively.43,44The synthesized CoFe2O4 film at pH 9 was sonicated in ethanol for 1 h and then imaged using a transmission electron microscope (TEM), Fig. 2. The TEM image in Fig. 2(a) indicates the uniform morphology of the sample. The HRTEM image (Fig. 2(b)) reveals perfect lattice fringes with inter-planar distances of 0.23 and 0.29 nm, respectively, owing to (222) and (220) planes of CoFe2O4. To gain more insights into the crystal structure of the material, grazing angle X-ray diffraction (XRD) spectra of the CoFe2O4/Ni foam were collected (Fig. 2(c)). Note that the high intensity peaks at 45° and 52° are correlated to the (111) and (200) planes of Ni foam with a small shift of the peak position due to the strain resulting from the growth of the ferrite film. Moreover, the three peaks at 30.8°, 36°, and 38.4° can be assigned to the (220), (311), and (222) planes of CoFe2O4.45 Note that the small peak shift in the CoFe2O4 spectra can be ascribed to the induced strain due to the growth on Ni foam. The XRD spectrum of the powder formed in the hydrothermal reactor at different pH values is presented in Fig. S1 (ESI†), confirming the formation of CoFe2O4 during the different synthesis conditions. The findings from TEM and XRD results are consistent. The Fourier transform infrared (FTIR) spectra show the characteristic features of spinel ferrites as displayed in Fig. 2(d). The observed two absorption bands in the range of 400–430 cm−1 are assigned to the stretching vibrations of the octahedral Co2+–O and Fe3+–O bonds. The band at ∼590 cm−1 is assigned to the stretching vibrations of the tetrahedral iron–oxygen bond and the band at 670 cm−1 is assigned to the stretching vibration of the tetrahedral cobalt–oxygen bond.46–50 Almost at 1630 cm−1, the O–H bending can be observed and the OH group of water adsorbed on the samples can be represented at around 3420 cm−1. The full FTIR spectrum for different pH values can be found in Fig. S2 (ESI†).
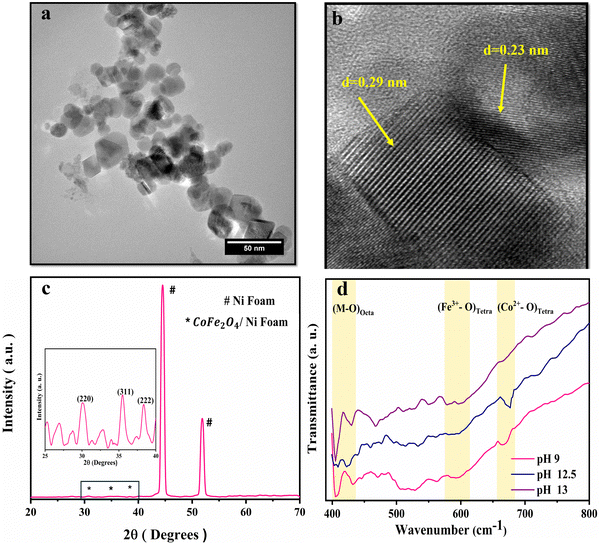 | ||
| Fig. 2 Structural characterization of CoFe2O4/Ni foam. (a) TEM image, (b) HRTEM image showing the d-spacing, (c) XRD spectra, and (d) FTIR spectra at different pH values. | ||
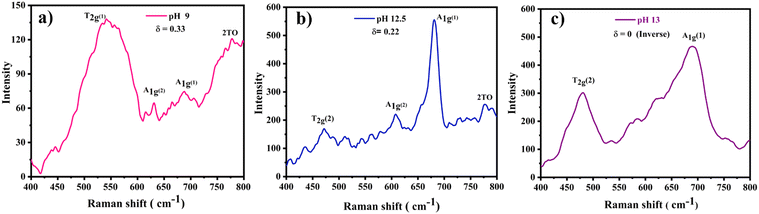
Moreover, to confirm the formation of CoFe2O4 and gain insights into the inversion degree of cation distribution in the formed structure, the Raman spectra were collected and analyzed, Fig. 3. The spectra show the characteristic Raman active modes of CoFe2O4 prepared at different pH values, namely A1g (1) and A1g (2), characteristic of the stretching vibrations of Fe–O and Co–O bonds in the tetrahedral sites.51,52 T2g(1) and T2g(2) are attributed to the asymmetric bending of oxygen ions in the M–O bond at octahedral sites and the 2TO band is due to the interaction of two transverse optical phonons.53–55 The degree of inversion (δ) was calculated based on the Raman spectrum using eqn (5):56
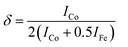 | (5) |
To elucidate the surface chemical composition of the material, X-ray photoelectron spectroscopy (XPS) analysis was utilized. The Fe 2p spectra of the sample fabricated at pH 9 Fig. 4(a) reveal two peaks characteristic of Fe 2p3/2 and Fe 2p1/2 at 712 and 722 eV, respectively. Deconvolution of the Fe 2p3/2 spectrum indicates three peaks positioned at 707, 711.88, and 713.58 eV, assigned to Fe0, Feoct3+, and Fetet3+, respectively, revealing the different distribution of Fe3+ at the octahedral site (Feoct3+) and tetrahedral site (Fetet3+).24 The shift of the Fetet3+ peak between the two samples may be due to the increase of Fe3+ ions in the tetrahedral site, resulting in higher shift for the binding energy of Fe3+. Fe0 appears to be a byproduct of the reaction with a small ratio, which might be due to the use of a reducing agent (NaOH) during the preparation.59 In the Co 2p high-resolution XPS spectrum (Fig. 4(b)), the peaks of Cooct2+ and Cotet2+ were observed at 779.9 and 782 eV for 2p3/2, showing the distribution of Co2+ at the octahedral site and tetrahedral site in the spinel structure.60,61 The doublet splitting of ∼15.4 confirms the formation of the CoFe2O4 layer.62,63 In addition, the ratio of the area under the peaks for both Cotet2+ and Cooct2+ was found to be 0.33, in agreement with the Raman analysis results. Note that the peak at 774 eV for Co is the Auger Co LMM peak. Also, the observed peak at ∼784.5 eV seems to correspond to either the Auger peak of Fe or the satellite peak of Co2p3/2.64Fig. 4(c) and (d) shows the Fe 2p spectra and Co 2p spectra of the sample fabricated at pH 13. The area under the peaks for the two elements changed owing to the change in the cation distribution among the samples as proven by the Raman spectra. As noticed for Co 2p in Fig. 4(d), the peak of Cotet2+ was not observed and only one peak attributed to Cooct2+ was noticed at 781.6 eV for 2p3/2, indicating the formation of the inverse structure. Fig. S3a and c (ESI†) depicts the high-resolution XPS scan of Ni 2p showing peaks at 855.48 and 873.48 eV, attributed to Ni2+ 2p3/2 and Ni2+ 2p1/2, respectively. Also, the high-resolution O 1s spectra in Fig. S3b and d (ESI†) reveal the coexistence of three oxygen species. The peak at 529.4 eV is owing to the metal–O bond, while the peaks at 530.9 and 532.48 eV are associated with oxygen in the hydroxide groups and oxygen species in the surface-adsorbed H2O molecules, respectively.63
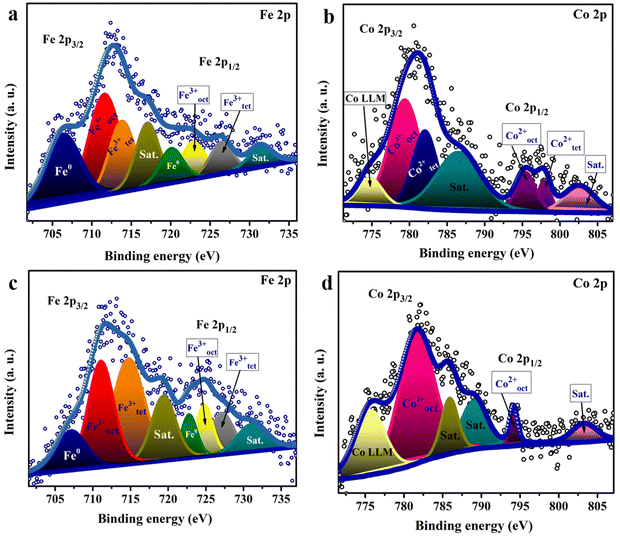 | ||
| Fig. 4 High resolution XPS scan of (a) Fe 2p and (b) Co 2p spectra of the catalyst fabricated at pH 9 and (c) Fe 2p and (d) Co 2p spectra of the catalyst synthesized at pH 13. | ||
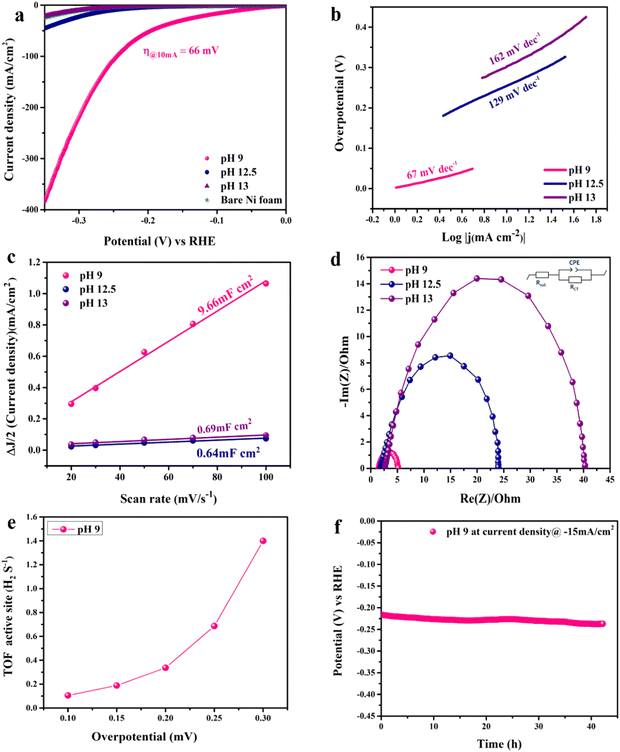
The electrocatalytic activity of the catalyst towards the HER was evaluated in 1.0 M KOH using a 3-electrode electrochemical cell. Fig. 5(a) shows the LSV scans in the cathodic direction. Note that LSV is iR-corrected for ohmic potential losses of the bare nickel foam used as the substrate compared to the prepared CoFe2O4/Ni foam electrodes. At the benchmark current of −10 mA cm−2, the LSV spectra reveal exceptional electrochemical activity of the prepared CoFe2O4 electrode prepared at pH 9 compared to the other samples fabricated at other pH values. iR-corrected LSV performed at different scan rates (2, 5, and 10 mV s−1) for the pH 9 sample to eliminate the effect of capacitive current is shown in Fig. S4 (ESI†). The estimated overpotential (η) was as low as 66 mV at −10 mA cm−2 with exceptional increase in the cathodic current density with increasing overpotential, indicative of the high catalytic activity of the material surpassing those of most of the reported ferrites prepared via more complex and multiple processing steps as listed in Table S1 (ESI†). Note that bare NF showed a high η of 290 mV at −10 mA cm−2, while the sample prepared at pH 12.5 showed η = 246 mV and the sample prepared at pH 13 showed η = 296 mV. The results showed the exceptional electrocatalytic activity of the prepared material, which can be attributed to the high catalytic activity of the prepared CoFe2O4 and the effect of the cation distribution within the material in addition to the interfacial interaction between the nickel foam and the CoFe2O4 spinel structure. The synergy between spinel and NF should facilitate charge transfer and HER kinetics due to the high conductivity of the system.37,65,66 Moreover, the 3D sheet-like structure also contributes to the high catalytic activity of the catalyst by providing plenty of active sites and enormous surface area, and the higher electrode–electrolyte interface area results in enhanced diffusion and adsorption of the reactant species.
Tafel analysis was used to get insights into the mechanistic pathways of the HER. Fig. 5(b) reveals Tafel slopes of 67, 129, and 162 mV dec−1, for the CoFe2O4/Ni foam electrodes synthesized at pH 9, 12.5, and 13, respectively. The obtained Tafel slopes suggest that the HER of the samples fabricated at pH 9 and pH 12.5 follows the Volmer–Heyrovsky mechanism, where hydrogen desorption (H2O + e− + H* → H2 + HO−) is the rate determining step.67,68 However, the lower Tafel slope of the CoFe2O4/Ni foam electrode at pH 9 indicates faster kinetics. In addition, the exchange current density (j0) of CoFe2O4 fabricated at pH 9 is ∼1 mA cm−2, while that of the counterpart samples prepared at pH 12.5 and pH 13 is ∼0.1 mA cm−2 for both, indicating the better kinetics of the HER on the surface of the CoFe2O4 electrode fabricated at pH 9. To gain in-depth insights into the inherent properties of the CoFe2O4/Ni foam catalyst, the electrochemical active surface area (ECSA) was calculated to estimate the capacitance of the double layer (Cdl) at the electrode/electrolyte interface. Note that Cdl is obtained from the cyclic voltammograms (CVs) at different scan rates by measuring the non-faradaic capacitive current related to the double layer charging as shown in Fig. S5a–c (ESI†) for the electrodes synthesized at pH 9, 12.5, and 13, respectively, and then taking the linear regression of the slope of the cathodic current and anodic current difference vs. the scan rate.
As presented in Fig. 5(c), for the pH 12.5-sample, the Cdl is 0.64 mF cm−2 and for the pH 13-sample, the Cdl is 0.69 mF cm−2 even though the catalytic activity of the pH 12.5-sample is higher than that of the pH 13-sample. The higher surface area does not necessarily indicate higher activity in this case; it might be due to the difference in the structure between the two samples.69 The Cdl of the pH 9-sample is 9.66 mF cm−2, which is 15 times higher than those of the other samples. This high Cdl indicates higher surface roughness and more catalytically active sites available on the surface of the CoFe2O4/Ni foam. ECSA was computed by dividing the Cdl of all the catalysts by the specific capacitance (Cs) of the flat surface, which is considered to be 40 μF cm−2,41 to accurately determine the area of the active sites. The ECSA values were found to be 241.5, 16, and 17.25 cm2 for the samples fabricated at pH 9, 12.5, and 13, respectively. The current density normalized ECSA of the three samples at different potentials is shown in Table S2 (ESI†). These results demonstrated that the sample prepared at pH 9 exhibits superior activity compared to those prepared at pH 12.5 and 13. This suggests that the catalytic performance is influenced not only by the surface area but also by the inherent activity of the active sites.
Since the charge transfer resistance at the electrode/electrolyte interface and electronic conductivity are important parameters determining the electrochemical activity, electrochemical impedance spectra (EIS) of the synthesized CoFe2O4 electrodes at different pH values were collected at −0.176 V vs. RHE and analyzed, Fig. 5(d). The spectra depict a semi-circle that was fitted by Randle's circuit (inset in Fig. 5(b)), revealing a charge transfer resistance (Rct), a solution resistance (Rsol), and a constant phase element (CPE) instead of an ideal capacitor due to the surface roughness of the nanostructured material as indicated by the depressing y-axis.70 The Rsol is almost the same for all samples, indicating that Rct is the one controlling the catalytic activity of the catalyst as well as the bare Ni foam. Upon comparing the Nyquist plots of all samples, the smallest semicircle of the pH 9-sample showed an Rct of 3.6 Ω, while the Rct values of pH 12.5- and 13-samples are 22.9 and 38.47 Ω, respectively. This result indicates that the cation distribution of the sample prepared at pH 9 and the coupling between CoFe2O4 and Ni foam enhanced the charge transfer at the electrode/electrolyte interface and the conductivity, resulting in higher current density and faster HER kinetics.69 In catalysis, one of the best figures of merits to assess and compare the catalytic activity of catalysts is to calculate the turnover frequency (TOF), which represents the amount of H2 generated per active site, as detailed in the ESI.† As illustrated in Fig. 5(e), the TOF of the pH 9-catalyst was found to be 18 × 10−2 s−1 at 150 mV, surpassing many of the reported HER electrocatalysts.71 The stability of the catalyst is another important merit that determines its potential use on a large scale. To assess the stability of the electrode, the chronopotentiometry test was carried out at −15 mA cm−2 for 44 h as shown in Fig. 5(f). The pH 9-catalyst showed steady current response with a minimal fluctuation of the overpotential of approximately 20 mV, revealing its long-term durability. The electrocatalytic activity of the CoFe2O4/Ni foam catalyst prepared at pH 9 surpassed those of most of the reported non-precious metal-based catalysts, Table S1 (ESI†).
Intrigued by the superior HER activity of the CoFe2O4/Ni foam catalyst, it was further tested in a 2-electrode water electrolyzer employing RuO2 as the counter electrode to minimize the OER overpotential, as depicted in the inset of Fig. 6(a). The polarization curve of the overall water splitting (Fig. 6(a)) reveals a cell voltage of 1.61 V to achieve a current density of 15 mA cm−2, corresponding to a low η of 0.38 V. The chronopotentiometric stability measurement (Fig. 6(b)) was performed in a 2-electrode water electrolyzer for about 50 h, with only a 20 mV increase in the overpotential over the entire 50 h of electrolysis, revealing the high stability of the electrode and its efficiency as an HER catalyst. Fig. S6 (ESI†) shows FESEM images of the electrode before and after the electrochemical and stability measurements, indicating the preservation of the unique sheet structure even after the aggressive tests. As an additional confirmation to prove the stability of the electrode, SEM-EDS and mapping analyses were performed on the electrode before and after stability measurement as depicted in Fig. S7 and S8 (ESI†). The results revealed the homogenous distribution of the elements (Fe, Co, and O) on the surface of the Ni foam not affected by the stability test. Thus, the prepared catalyst is stable and durable for the HER. The amount of H2 produced was determined via the water displacement method in an H-type cell having two compartments, where the cathode and the anode were separated by a Nafion membrane. The amount of gas was quantified during electrolysis at 20 mA cm−2 over different time intervals. As shown in Fig. 6(c), the amount measured experimentally is roughly in agreement with the theoretically calculated values with FE approaching 100%.
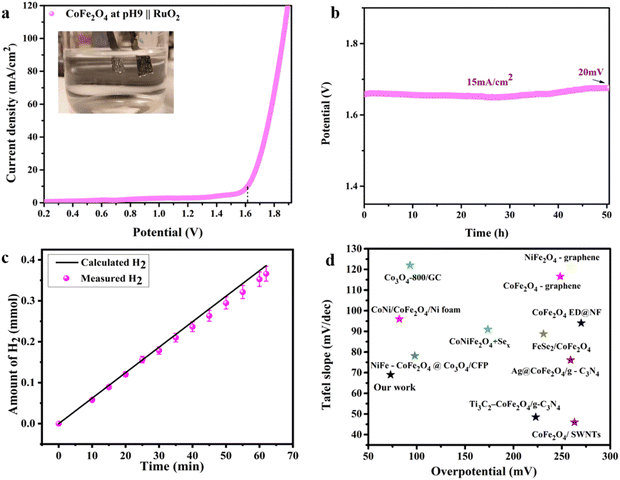 | ||
Fig. 6 The overall water splitting electrolyzer performance determined using the pH 9 CoFe2O4 electrocatalyst as the cathode and RuO2 as the anode in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) M KOH solution. (a) iR-compensated LSV plot at a 10 mV s−1 scan rate, (b) CP durability test recorded at 15 mA cm−2, (c) the amount of gas determined experimentally and theoretically vs. time at 20 mA cm−2 and (d) comparison of the HER electrocatalytic activity of the CoFe2O4-based catalysts (ref. 63 and 72–80). M KOH solution. (a) iR-compensated LSV plot at a 10 mV s−1 scan rate, (b) CP durability test recorded at 15 mA cm−2, (c) the amount of gas determined experimentally and theoretically vs. time at 20 mA cm−2 and (d) comparison of the HER electrocatalytic activity of the CoFe2O4-based catalysts (ref. 63 and 72–80). | ||
Therefore, the above findings indicate the potential of the prepared CoFe2O4/Ni foam as a promising low-cost HER catalyst, which has the advantages of high activity, easy preparation, and long-term stability characteristics. Fig. 6(d) compares the HER electrocatalytic activity of CoFe2O4-based catalysts, revealing the superiority of our catalyst, in agreement with the data in Table S1 (ESI†). From the catalysis point of view, it has been observed that octahedral sites tend to possess a higher catalytic activity compared to tetrahedral sites due to their exceptional geometric and electronic properties, which make them more favorable for participating in catalytic reactions.28 When the inversion parameter is higher, a larger proportion of Fe atoms occupy the octahedral sites. Increasing the inversion parameter means increasing the amount of iron in the octahedral sites, which would result in a better catalytic activity of the material, i.e. the HER in our case. The reasons behind this activity might be assigned to the role of Fe existing in the octahedral sites in adjusting the electronic structure of the material, resulting in an improvement of the electron transfer processes throughout the HER.81 Generally, the integration of more active octahedral sites with increasing amount of iron in those sites with a higher inversion parameter results in a material that exhibits better catalytic activity towards the HER.
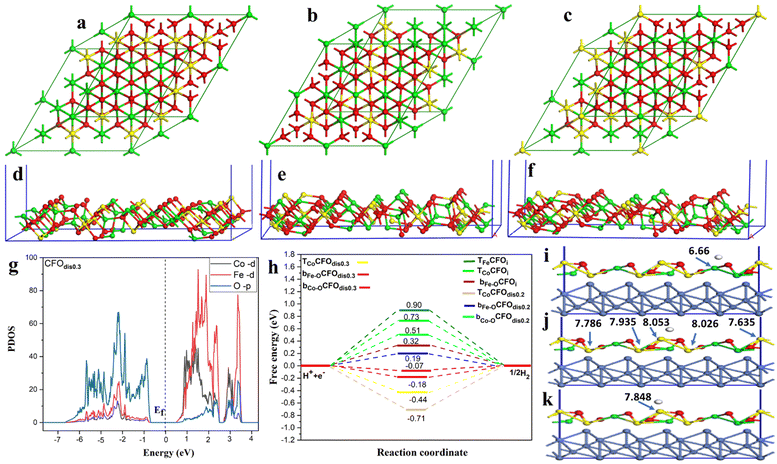
To unveil the experimentally observed superior HER activity of the fabricated distorted inverse spinel CoFe2O4 (CFOdis), density functional theory (DFT) calculations were conducted. In an ideal inverse spinel (CFOi), Fe occupies all tetrahedral sites (Td) and half of the octahedral sites (Oh), and Co occupies only half of the octahedral sites, Fig. 7(a). However, Fig. 7(b) and (c) shows CFOdis0.2 and CFOdis0.3, respectively, where both Co and Fe atoms occupy octahedral and tetrahedral sites in the above-mentioned ratios. The distribution of the metals in the octahedral and tetrahedral sites has a great effect on the catalytic activity. It was noticed from Fig. 7(d)–(f) that the upper layer of the 311 CFOdis0.3 surface has more Co sites than those of 311 CFOdis0.2 and 311 CFOi surfaces, respectively, which affects the HER catalytic activity.
Charge transfer is one of the most important surface descriptors that has a strong effect on the adsorption energy and facilitates the determination of the active sites for hydrogen adsorption. To this end, various possible active sites were considered, Fig. 7(i)–(k), the bridge between Fe and O denoted as bFe–O, the bridge between Co and O denoted as bCo–O, and top Co atom (TCo) sites. Bader charge analysis was performed on each atom and its net charge was calculated for CFOdis0.3. Negative charge means accepting electrons, while a positive value refers to donation of electrons. It was observed that Bader charges of Co atoms on the surface before H adsorption were 8.145 e, 8.091 e, 7.972 e, 7.848 e, and 7.679 e. After adsorption on the top Co site, there was a charge transfer from the Co atom binding with the hydrogen atom (TCo) from 8.145 e to 7.848 e, indicating charge transfer from TCo to the incoming hydrogen by −0.297 e, suggesting strong adsorption. Besides, after adsorption on the bridge between Co and O, the charges on the neighboring Co atoms were 8.053 e, 8.026 e, 7.935 e, 7.786 e, and 7.635 e, indicating a total charge transfer from the surrounding atoms of −0.255 e to the adsorbed hydrogen. For the Fe atom, Bader charges were found to be 6.800 e and 6.66 e before and after H adsorption on the bridge between Fe and O, respectively, indicating a little charge transfer to the hydrogen atom of −0.14 e and weaker adsorption than the other sites. The partial density of states (PDOS) reveals the semiconducting behavior of the CFO as depicted in Fig. 7(g) and Fig. S9 (ESI†). Observing the PDOS for CFOdis0.3, the valence band is dominated by overlapping of oxygen p orbitals while the conduction band is dominated by overlapping of FeTd, FeOh, CoOh, and CoTd. Also, the position of the d-band center from the Fermi level (Ef) is a good indicator of the catalytic activity of the catalyst.82 The nearer the d-band center to the Ef, the better the electrocatalytic activity. The distorted structures have an up-shifted d-band center position towards the Ef from −2.35 eV for CFOi to −1.89 eV for CFOdis0.2 and −1.247 eV for CFOdis0.3, which could explain the obtained enhanced activity. The d-band center (Ed) was estimated using eqn (6):
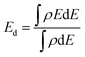 | (6) |
As the HER involves adsorption and desorption of hydrogen, Gibbs free energy (ΔGH*) was found to be a good descriptor of HER activity.83–86 A superior catalyst should have a ΔGH* value near zero, as ΔGH* greater than zero means that the catalyst has weak affinity for adsorption. Also, ΔGH* much less than zero indicates sturdy adsorption, which inhibits desorption of hydrogen. Both cases require overpotential for the HER. According to the Sabatier principle, for better catalytic activity, the adsorption of hydrogen should not be too robust or too weak. It should be intermediary. The adsorption energy for hydrogen was calculated using eqn (7) and the Gibbs free energy was computed according to eqn (8):
| ΔE = Esurf+H − Esurf − 1/2E(H2) | (7) |
| ΔG = ΔE + ΔZPE − TΔS | (8) |
Conclusion
The appropriate design and fabrication of cost-effective, durable, and efficient electrocatalysts for water splitting are essential to realize sustainable hydrogen production. The exploration of non-noble metal electrocatalysts, such as spinel ferrite nanoparticles, and the use of suitable conducting substrates, such as nickel foam, have shown promising results in enhancing the stability and electrocatalytic activity of these electrocatalysts for the water-splitting process. However, most of the studies are based on trial-and-error methods in selecting the catalysts. Further development and optimization of the catalysts necessitate the identification of crucial descriptors that govern the activity of such catalysts. This study introduced the cation distribution, i.e., the degree of inversion (δ), as a valuable descriptor to design efficient electrocatalysts. A facile yet optimized hydrothermal method was used to prepare CoFe2O4 as an efficient HER catalyst with different cation distributions (δ = 0, 0.22, and 0.33). The experimental measurements revealed that the sample with the high cation distribution possesses a high electrochemical active surface area, good stability over 44 h of continuous electrolysis and high TOF, confirming the high catalytic activity of the catalyst toward the HER with a low overpotential of 66 mV at −10 mA cm−2. The high catalytic activity was ascribed to the cation distribution as revealed by the XPS and Raman analyses and supported by the DFT calculations. We hope this work will inspire more insightful studies on the identification, design, and fabrication of a plethora of efficient electrocatalysts.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
The American University in Cairo is highly appreciated for supporting this work. This work was also supported by computational resources provided by the Bibliotheca Alexandrina on its High-Performance Computing (HPC) infrastructure (see hpc.bibalex.org).Notes and references
- S. Chu and A. Majumdar, Nature, 2012, 488, 294–303 CrossRef CAS PubMed.
- A. Pareek, R. Dom, J. Gupta, J. Chandran, V. Adepu and P. H. Borse, Mater. Sci. Energy Technol., 2020, 3, 319–327 CAS.
- G. Li, G. Han, L. Wang, X. Cui, N. K. Moehring, P. R. Kidambi, D. Jiang and Y. Sun, Nat. Commun., 2023, 14, 525 CrossRef CAS PubMed.
- S. Anwar, F. Khan, Y. Zhang and A. Djire, Int. J. Hydrogen Energy, 2021, 46, 32284–32317 CrossRef CAS.
- F. M. Sapountzi, J. M. Gracia, C. J(.Kees-J). Weststrate, H. O. A. Fredriksson and J. W(.Hans) Niemantsverdriet, Prog. Energy Combust. Sci., 2017, 58, 1–35 CrossRef.
- K. E. Salem, A. A. Saleh, G. E. Khedr, B. S. Shaheen and N. K. Allam, Energy Environ. Mater., 2023, 6, e12324 CrossRef CAS.
- Q. Xu, J. Zhang, H. Zhang, L. Zhang, L. Chen, Y. Hu, H. Jiang and C. Li, Energy Environ. Sci., 2021, 14, 5228–5259 RSC.
- M. M. Hasan, A. K. Gomaa, G. E. Khedr, K. E. Salem, B. S. Shaheen and N. K. Allam, Energy Fuels, 2022, 36, 14371–14381 CrossRef CAS.
- F. Guo, T. J. Macdonald, A. J. Sobrido, L. Liu, J. Feng and G. He, Adv. Sci., 2023, 10, 2301098 CrossRef CAS PubMed.
- S. Anantharaj, S. R. Ede, K. Sakthikumar, K. Karthick, S. Mishra and S. Kundu, ACS Catal., 2016, 6, 8069–8097 CrossRef CAS.
- P. Chen, J. Ye, H. Wang, L. Ouyang and M. Zhu, J. Alloys Compd., 2021, 883, 160833 CrossRef CAS.
- Y. Wang, B. Kong, D. Zhao, H. Wang and C. Selomulya, Nano Today, 2017, 15, 26–55 CrossRef CAS.
- T. Xiong, Z. Zhu, Y. He, M. Sadee, M. S. Balogun and Y. Huang, Small Methods, 2023, 7, 2201472 CrossRef CAS.
- S. Wang, A. Lu and C. J. Zhong, Nano Convergence, 2021, 8, 4 CrossRef CAS PubMed.
- S. Anantharaj, S. R. Ede, K. Karthick, S. Sam Sankar, K. Sangeetha, P. E. Karthik and S. Kundu, Energy Environ. Sci., 2018, 11, 744–771 RSC.
- A. Chirila, Y. Hu, J. C. Linehan, D. A. Dixon and E. S. Wiedner, J. Am. Chem. Soc., 2024, 146, 6866–6879 CrossRef CAS PubMed.
- A. Kumar, G. Zhang, W. Liu and X. Sun, J. Electroanal. Chem., 2022, 922, 116799 CrossRef CAS.
- L. Giordano, K. Akkiraju, R. Jacobs, D. Vivona, D. Morgan and Y. Shao-Horn, Acc. Chem. Res., 2022, 55, 298–308 CrossRef CAS PubMed.
- S. Jiao, X. Fu and H. Huang, Adv. Funct. Mater., 2021, 32, 2107651 CrossRef.
- S. González-Poggini, Int. J. Hydrogen Energy, 2024, 59, 30–42 CrossRef.
- Z. Xie, X. Huang, Z. Zhang and H. Xu, Phys. Chem. Chem. Phys., 2021, 23, 15101–15106 RSC.
- N. N. Huyen, L. M. Tung, T. A. Nguyen, T. L. Huong Phung, P. D. Thang, N. T. Vinh, Q. Van Nguyen, T. K. Oanh Vu, V. D. Lam, V. K. Le, N. X. Dinh and A.-T. Le, J. Phys. Chem. C, 2023, 127, 12262–12275 CrossRef CAS.
- J. K. Sharma, P. Srivastava, G. Singh and H. S. Virk, Solid State Phenom., 2015, 241, 126–138 Search PubMed.
- K. R. Sanchez-Lievanos, J. L. Stair and K. E. Knowles, Inorg. Chem., 2021, 60, 4291–4305 CrossRef CAS PubMed.
- S. J. Salih and W. M. Mahmood, Heliyon, 2023, 9, e16601 CrossRef CAS PubMed.
- N. M. Malima, M. D. Khan, S. C. Masikane, F. M. de Souza, J. Choi, R. K. Gupta and N. Revaprasadu, Sci. Rep., 2023, 13, 22179 CrossRef CAS PubMed.
- A. Tahir, F. Arshad, T. ul Haq, I. Hussain, S. Z. Hussain and H. ur Rehman, ACS Appl. Nano Mater., 2023, 6, 1631–1647 CrossRef CAS.
- S. K. Dutta, M. Akhter, J. Ahmed, M. K. Amin and P. K. Dhar, Biointerface Res. Appl. Chem., 2022, 12, 4399–4416 CAS.
- L. Chen, H. Hu, Y. Chen, J. Gao and G. Li, Chem. – Eur. J., 2021, 27, 7444–7452 CrossRef CAS PubMed.
- K. Ueda, M. Tsuji, J. Ohyama and A. Satsuma, Catal. Today, 2023, 411–412, 113816 CrossRef CAS.
- N. M. Refat, M. Y. Nassar and S. A. Sadeek, RSC Adv., 2022, 12, 25081–25095 RSC.
- J. X. Flores-Lasluisa, F. Huerta, D. Cazorla-Amorós and E. Morallón, Environ. Res., 2022, 214, 113731 CrossRef CAS PubMed.
- C. Wei, Z. Feng, G. G. Scherer, J. Barber, Y. Shao-Horn and Z. J. Xu, Adv. Mater., 2017, 29, 1–8 Search PubMed.
- X.-Y. Zhang, J.-Y. Xie, Y. Ma, B. Dong, C.-G. Liu and Y.-M. Chai, Chem. Eng. J., 2022, 430, 132312 CrossRef CAS.
- Y. Liu, Y. Ying, L. Fei, Y. Liu, Q. Hu, G. Zhang, S. Y. Pang, W. Lu, C. L. Mak, X. Luo, L. Zhou, M. Wei and H. Huang, J. Am. Chem. Soc., 2020, 141, 8136–8145 CrossRef PubMed.
- D. Wang, Y. Xu, X. Guo, Z. Fu, Z. Yang and W. Sun, J. Alloys Compd., 2021, 870, 159472 CrossRef CAS.
- M. Das, Z. B. Khan, M. Banerjee, A. Biswas and R. S. Dey, Catal. Today, 2023, 424, 113836 CrossRef CAS.
- A. M. Elbanna, A. M. Mohamed, L. G. Ghanem, H. M. El Sharkawy, G. E. Khedr and N. K. Allam, ACS Appl. Eng. Mater., 2024, 2, 35–48 CrossRef CAS.
- G. E. Khedr, S. M. Fawzy and N. K. Allam, J. CO2 Util., 2023, 78, 102619 CrossRef CAS.
- A. M. Asran, M. A. Mohamed, G. E. Khedr, G. M. G. Eldin, A. M. Yehia, R. K. Mishra and N. K. Allam, J. Therm. Anal. Calorim., 2022, 147, 5779–5786 CrossRef CAS.
- C. C. L. McCrory, S. Jung, J. C. Peters and T. F. Jaramillo, J. Am. Chem. Soc., 2013, 135(45), 16977–16987 CrossRef CAS PubMed.
- H. Gao, J. Xiang and Y. Cao, Appl. Surf. Sci., 2017, 413, 351–359 CrossRef CAS.
- D. A. Links, CrystEngComm, 2012, 14, 2213–2221 RSC.
- L. Chen, H. Wang, Y. Li and Q. Jiang, CrystEngComm, 2014, 16, 448–454 RSC.
- S. Mitra, P. S. Veluri, A. Chakraborthy and R. K. Petla, ChemElectroChem, 2014, 1, 1068–1074 CrossRef CAS.
- I. Sharifi, H. Shokrollahi, M. M. Doroodmand and R. Safi, J. Magn. Magn. Mater., 2012, 324, 1854–1861 CrossRef CAS.
- M. Kurian, S. Thankachan, D. S. Nair, A. E. K, A. Babu, A. Thomas and B. Krishna K. T, J. Adv. Ceram., 2015, 4, 199–205 CrossRef CAS.
- F. Paquin, J. Rivnay, A. Salleo, N. Stingelin and C. Silva, J. Mater. Chem. C, 2015, 3, 10715–10722 RSC.
- B. Jeevanantham, Y. Song, H. Choe and M. K. Shobana, Mater. Lett.: X, 2021, 12, 100105 CAS.
- M. M. El-Masry and R. Ramadan, Appl. Phys. A: Mater. Sci. Process., 2022, 128, 110 CrossRef CAS.
- P. Chandramohan, M. P. Srinivasan, S. Velmurugan and S. V. Narasimhan, J. Solid State Chem., 2011, 184, 89–96 CrossRef CAS.
- S. M. Ansari, K. C. Ghosh, R. S. Devan, D. Sen, P. U. Sastry, Y. D. Kolekar and C. V. Ramana, ACS Omega, 2020, 5, 19315–19330 CrossRef CAS PubMed.
- V. Bartůněk, D. Sedmidubský, Š. Huber, M. Švecová, P. Ulbrich and O. Jankovský, Materials, 2018, 11, 1241 CrossRef PubMed.
- R. S. Yadav, I. Kuřitka, J. Vilcakova, J. Havlica, J. Masilko, L. Kalina, J. Tkacz, J. Švec, V. Enev and M. Hajdúchová, Adv. Nat. Sci.: Nanosci. Nanotechnol., 2017, 8, 045002 Search PubMed.
- N. Mironova-Ulmane, A. Kuzmin, I. Sildos and M. Pärs, Cent. Eur. J. Phys., 2011, 9, 1096–1099 CAS.
- H. D. T. Duong, D. T. Nguyen and K.-S. Kim, Nanomaterials, 2021, 11, 3056 CrossRef CAS PubMed.
- V. Georgiadou, V. Tangoulis, I. Arvanitidis, O. Kalogirou and C. Dendrinou-Samara, J. Phys. Chem. C, 2015, 119, 8336–8348 CrossRef CAS.
- S. Suharyana, R. R. Febriani, N. P. Prasetya, U. Utari, N. A. Wibowo, S. Suharno, A. Supriyanto, A. H. Ramelan and B. Purnama, Kuwait J. Sci., 2023, 50, 575–579 CrossRef.
- H. Sun, X. Yang, L. Zhao, T. Xu and J. Lian, J. Mater. Chem. A, 2016, 4, 9455–9465 RSC.
- Z. Zhou, Y. Zhang, Z. Wang, W. Wei, W. Tang, J. Shi and R. Xiong, Appl. Surf. Sci., 2008, 254, 6972–6975 CrossRef CAS.
- K. Chakrapani, G. Bendt, H. Hajiyani, I. Schwarzrock, T. Lunkenbein, S. Salamon, J. Landers, H. Wende, R. Schlögl, R. Pentcheva, M. Behrens and S. Schulz, ChemCatChem, 2017, 9, 2988–2995 CrossRef CAS.
- C. Xiao, Y. Li, X. Lu and C. Zhao, Adv. Funct. Mater., 2016, 26, 3515–3523 CrossRef CAS.
- S. Li, S. Sirisomboonchai, A. Yoshida, X. An, X. Hao, A. Abudula and G. Guan, J. Mater. Chem. A, 2018, 6, 19221–19230 RSC.
- A. Kumar, T. Shripathi and P. C. Srivastava, J. Sci. Adv. Mater. Devices, 2016, 1, 290–294 CrossRef.
- X. Hu, X. Tian, Y.-W. Lin and Z. Wang, RSC Adv., 2019, 9, 31563–31571 RSC.
- S. Riyajuddin, K. Azmi, M. Pahuja, S. Kumar, T. Maruyama, C. Bera and K. Ghosh, ACS Nano, 2021, 15(3), 5586–5599 CrossRef CAS PubMed.
- F. Bao, E. Kemppainen, I. Dorbandt, R. Bors, F. Xi, R. Schlatmann, R. van de Krol and S. Calnan, ChemElectroChem, 2021, 8, 195–208 CrossRef CAS.
- L. Huang, Y. Hou, Z. Yu, Z. Peng, L. Wang, J. Huang, B. Zhang, L. Qian, L. Wu and Z. Li, Int. J. Hydrogen Energy, 2017, 42, 9458–9466 CrossRef CAS.
- S. I. Perez Bakovic, P. Acharya, M. Watkins, H. Thornton, S. Hou and L. F. Greenlee, J. Catal., 2021, 394, 104–112 CrossRef CAS.
- S. Anantharaj and S. Noda, ChemElectroChem, 2020, 7, 2297–2308 CrossRef CAS.
- Y. Zhu, H. A. Tahini, Z. Hu, J. Dai, Y. Chen, H. Sun, W. Zhou, M. Liu, S. C. Smith, H. Wang and Z. Shao, Nat. Commun., 2019, 10, 149 CrossRef PubMed.
- P. Muthukumar, M. Pannipara, A. G. Al-Sehemi, D. Moon and S. P. Anthony, New J. Chem., 2022, 46, 12558–12564 RSC.
- Y. Lin, J. Wang, D. Cao and Y. Gong, Sustainable Energy Fuels, 2020, 4, 1933–1944 RSC.
- S. Mathew, R. Madhushree and K. R. S. Devi, Sustainable Energy Fuels, 2023, 7, 2601–2612 RSC.
- M. J. Sadiq Mohamed, S. Caliskan, M. A. Gondal, M. A. Almessiere, A. Baykal, Y. Slimani, K. A. Elsayed, M. Hassan, I. A. Auwal, A. Z. Khan, A. A. Tahir and A. Roy, ACS Appl. Nano Mater., 2023, 6, 7330–7341 CrossRef CAS.
- R. Nivetha, S. Chella, P. Kollu, S. K. Jeong, A. Bhatnagar and N. G. Andrews, J. Magn. Magn. Mater., 2018, 448, 165–171 CrossRef CAS.
- H. Zhang, L. Nengzi, B. Li, Q. Cheng, J. Gou and X. Cheng, Renewable Energy, 2020, 155, 717–724 CrossRef CAS.
- C. Zhang, S. Bhoyate, C. Zhao, P. Kahol, N. Kostoglou, C. Mitterer, S. Hinder, M. Baker, G. Constantinides, K. Polychronopoulou, C. Rebholz and R. Gupta, Catalysts, 2019, 9, 176 CrossRef.
- Y. Ding, J. Zhao, W. Zhang, J. Zhang, X. Chen, F. Yang and X. Zhang, ACS Appl. Energy Mater., 2019, 2, 1026–1032 CrossRef CAS.
- A. Zabielaite, O. Eicher-Lorka, Z. Kuodis, R. Levinas, D. Simkunaite, L. Tamasauskaite-Tamasiunaite and E. Norkus, Crystals, 2023, 13, 1342 CrossRef CAS.
- Y. Sun, A. Huang and Z. Wang, RSC Adv., 2019, 9, 26321–26326 RSC.
- W. Qiao, S. Yan, D. Jin, X. Xu, W. Mi and D. Wang, J. Phys.: Condens. Matter, 2021, 33, 245201 CrossRef CAS PubMed.
- I. M. Badawy, G. E. Khedr, A. M. Hafez, E. A. Ashour and N. Allam, Chem. Commun., 2023, 59, 7974–7977 RSC.
- A. M. Agour, E. Elkersh, G. E. Khedr, H. G. El-Aqapa and N. K. Allam, ACS Appl. Nano Mater., 2023, 6(17), 15980–15989 CrossRef CAS.
- H. G. El-Aqapa, I. M. Badawy, G. E. Khedr, A. M. Agour, D. M. Sayed, M. M. Taha and N. K. Allam, Catal. Sci. Technol., 2023, 13, 5175–5179 RSC.
- S. M. Fawzy, G. E. Khedr and N. K. Allam, Int. J. Hydrogen Energy, 2023, 48, 33111–33118 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ey00121d |
| ‡ Both authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |