Valley-selective carrier transfer in SnS-based van der Waals heterostructures

Abstract

Valleytronics, i.e., use of the valley degree of freedom in semiconductors as an information carrier, is a promising alternative to conventional approaches for information processing. Transition metal dichalcogenides with degenerate K/K′ valleys have received attention as prototype 2D/layered semiconductors for valleytronics, but these systems rely on exotic effects such as the valley-Hall effect for electrical readout of the valley occupancy. Non-traditional valleytronic systems hosting sets of addressable non-degenerate valleys could overcome this limitation. In the van der Waals semiconductor Sn(II) sulfide (SnS), for instance, different bandgaps and band edges may allow manipulating the population of the X- and Y-valleys via charge transfer across interfaces to other layered semiconductors. Here, we establish this concept by comparing SnS flakes and SnS-based heterostructures. Cathodoluminescence spectroscopy shows a striking reversal of the luminescence intensity of the two valleys in SnS–GeS van der Waals stacks, which stems from a selective electron transfer from the Y-valley into GeS while X-valley electrons remain confined to SnS. Our results suggest that non-traditional systems, embodied here by SnS-based van der Waals heterostructures, open avenues for valley-selective readout relying on design parameters such as heterostructure band offsets that are among the core concepts of semiconductor technology.

---

New concepts

Valleytronics, using the valley degree of freedom in semiconductors as an information carrier, represents a promising alternative to conventional approaches for information processing. So far, transition metal dichalcogenides with degenerate valley states have received attention as 2D/layered semiconductors for valleytronics, but they have the disadvantage of relying on exotic effects for electrical readout of the valley state. Here, we explore the properties of non-traditional valleytronic materials that harbor sets of non-degenerate valleys, using the layered semiconductor Sn(II) sulfide (SnS) as a model system. With their different bandgaps and valence/conduction band edges, the two (X, Y) valleys in SnS promise the unique ability to manipulate the valley-state via charge transfer across interfaces to other layered semiconductors. We address this possibility in SnS flakes and SnS-based heterostructures. Cathodoluminescence shows a striking reversal of the emission intensity of the X- and Y-valleys in SnS–GeS van der Waals stacks, which implies a selective electron transfer from the Y-valley into GeS while X-valley electrons remain confined to SnS. Our results show that unconventional valleytronic systems, such as SnS-based heterostructures, enable avenues for valley-selective readout relying on design parameters such as heterostructure band offsets that are among the core concepts of semiconductor technology.

Introduction

The electronic band structure of many semiconductors comprises several competing extrema in the valence- or conduction bands straddling the fundamental bandgap, which are referred to as valleys. A classic example is silicon, whose band structure involves six symmetry-equivalent (i.e., degenerate) conduction-band valleys located along the Γ–X line in reciprocal space. The field of valleytronics is based on the premise that the occupancy of different valleys could be used as an information carrier.¹ Early efforts toward this end included studies on the lifting of the valley degeneracy in Si inversion layers near high-index surfaces.^2,3 More recent work has built on these early findings by considering factors such as confinement and strain to lift the valley degeneracy and manipulate different valley states in Si.⁴

With the advent of two-dimensional (2D) semiconductors, avenues for addressing the valley degree of freedom have received renewed interest. The most studied systems include hexagonal transition metal dichalcogenides (TMDs) MX₂, where M = Mo, W and X = S, Se. As in the semimetal graphene, the degenerate band-edge states in these semiconductors occur at two types of inequivalent K-points (referred to as K and K′) at the edge of the 2D Brillouin zone. The K/K′ valleys can be represented by a pseudospin that behaves like a (two-state) spin-½ system. It has been shown that the degenerate valleys in these systems can be addressed optically via circularly polarized light with opposite helicity.^5,6 To address the valleys electrically, however, one has to rely on exotic phenomena, such the valley Hall effect^7,8 that arises from the opposite Berry curvatures of the two types of valleys in systems that lack inversion symmetry, notably monolayer TMDs.⁹ Other control strategies rely on the application of magnetic fields and the valley-Zeeman effect^10–12 to lift the inherent degeneracy of the K/K′ valleys.

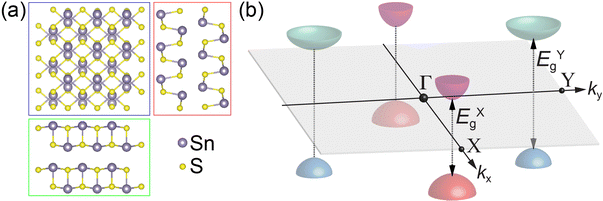
An alternative approach toward utilizing the valley degree of freedom involves semiconductors with multiple symmetry-distinct valleys that are not degenerate, i.e., whose interband transitions occur at different energies. A prototype system representing this class of valleytronic materials is tin(II) sulfide (SnS), an orthorhombic layered monochalcogenide semiconductor whose structure resembles that of black phosphorus (Fig. 1(a)).¹³ In SnS, pairs of valleys located along the orthogonal Γ–X and Γ–Y lines in k-space give rise to distinct bandgaps, i.e., they are inherently non-degenerate (Fig. 1(b)).¹⁴ Optical selection rules for the X- and Y-valleys imply that they can be addressed by linearly polarized light,¹⁴ both in absorption and photoluminescence.¹⁵ Such systems present opportunities for valley-selective electrical readout based on carrier transfers at interfaces, e.g., in heterostructures with suitable band offsets.

Fig. 1 Crystal structure and band edges of orthorhombic SnS. (a) Crystal structure of SnS (space group Pnma). Red, green, and blue boxes show views along [100], [010], and [001] axes. (b) Schematic illustration of the valence- and conduction band edges of SnS along k_x and k_y reciprocal space axes, with bandgaps E^X_g and E^Y_g of the non-degenerate X- and Y-valleys, respectively.

Here, we report experiments demonstrating the valley-selective carrier extraction in SnS-based heterostructures. Although the ultimate goal is the electrical readout of the carrier population of the valleys, we find that local luminescence spectroscopy – implemented via electron-beam excited cathodoluminescence in scanning transmission electron microscopy (STEM-CL) – lends itself ideally for interrogating relative changes in the carrier population in the two valleys due to the valley-selective extraction of carriers across interfaces. By comparing measurements on homogeneous multilayer SnS flakes, SnS–SnS₂ wrap-around core–shell heterostructures,¹⁶ and SnS–GeS lateral/vertical heterostructures,^17,18 we demonstrate how interfaces to other layered crystals lead to the same (type II) band alignment for both valleys in SnS–SnS₂, or different alignments for the X-valley (type I) and Y-valley (type II) at the SnS–GeS van der Waals interface. The latter gives rise to a striking inversion of the ratio between X- and Y-valley luminescence intensities that accompanies the selective carrier transfer from the SnS Y-valley into GeS. The CL results also support the notion that intervalley scattering¹⁹ in this system is sufficiently slow to allow an efficient transfer of carriers from a particular valley across a heterointerface. The reported findings represent an important step toward device architectures based on an unconventional valleytronic system with competing non-degenerate valleys, where the valley degree of freedom is used to encode, process, or store information.

Results and discussion

The growth of homogeneous SnS flakes was performed by a vapor transport process on mica substrates. Use of SnS powder as a growth precursor yields SnS flakes that are single crystalline with lateral sizes typically exceeding 5 μm, terminated by {110} side facets, as illustrated by the transmission electron microscopy (TEM) image in Fig. 2(a) and nanobeam electron diffraction pattern in Fig. 2(b). High-resolution TEM (Fig. 2(c)) shows the lattice fringes of SnS throughout the entire flake up to the surface without any detectable moiré patterns or other lattice fringes, thus corroborating the homogeneous composition of the flakes with only one crystalline phase, namely orthorhombic SnS with space group Pnma. Raman spectroscopy shows the characteristic modes of SnS across such flakes (Fig. S1(a) and (b), ESI†),²⁰ further supporting these conclusions.

Fig. 2 Structure and morphology of homogeneous SnS flakes. (a) TEM image of an entire SnS flake (side length 9.4 μm). (b) Nanobeam electron diffraction pattern of the flake, identifying the major side facets as {110} facets. (c) High-resolution TEM image showing SnS lattice fringes throughout the flake up to the free surface.

In order to create SnS flakes with interfaces that enable the manipulation of excited states, two types of heterostructures were synthesized: SnS–SnS₂ wrap-around core–shell heterostructures¹⁶ and SnS–GeS multilayer heterostructures.^17,18 The former were grown by vapor transport using an SnS₂ precursor. The SnS₂ precursor promotes large, thin SnS flakes by thermally decomposing to SnS and S,²¹ thereby providing both an SnS source and excess sulfur required for limiting vertical growth.²² Toward the end of the growth process, excess S is incorporated near the surface to produce a crystalline few-layer SnS₂ shell encapsulating the single-crystalline SnS core.¹⁶ An example of such a heterostructure is shown in Fig. 3(a–d). High-angle annular dark-field scanning TEM (HAADF-STEM, Fig. 3(a) illustrates the overall morphology of the heterostructures comprising a large, crystalline core of layered SnS that is again terminated by (110) majority side facets (Fig. 3(b)). High-resolution TEM shows the lattice fringes due to the wrap-around SnS₂ shell at the surface facets (Fig. 3(c)) as well as a stripe moiré pattern due to the superposition of the SnS and SnS₂ crystal lattices in the vertical SnS₂–SnS van der Waals stack across the large (001)^SnS top facet (Fig. 3(d)). Raman linescans primarily show the characteristic modes of SnS, consistent with the majority SnS phase in the core–shell structures (Fig. S1(c and d), ESI†). Averaging the individual spectra across the entire flake enhances the signal to noise ratio sufficiently to detect the major (A₁) mode of SnS₂,^16,23 originating from the few-layer SnS₂ shell (Fig. S1(e and f), ESI†).

Fig. 3 SnS-based heterostructures. (a)–(d) SnS–SnS₂ wrap-around core–shell heterostructures. (a) HAADF-STEM images of an SnS–SnS₂ heterostructure flake. (b) Electron diffraction pattern of the flake in (a), indexed to the primary SnS phase (zone axis [001]). (c) TEM image of part of the flake showing a stripe moiré pattern visible across the entire flake. (d) Higher magnification TEM image of the stripe moiré. (e)–(h) SnS–GeS multilayer heterostructures. (e) and (f) HAADF-STEM images of SnS–GeS heterostructures, showing a darker GeS lateral band surrounding a vertically stacked SnS–GeS center with brighter contrast. (g) TEM images of three SnS–GeS heterostructures with different thicknesses. (h) High-resolution TEM of the SnS–GeS moiré pattern detected in the central region (white rectangle in (g)).

Sequential growth of GeS on SnS seed flakes produces a different type of heterostructure that combines both lateral and vertical interfaces between the layered monochalcogenide crystals (Fig. 3(e and h)).^18,24 These combined (lateral/vertical) heterostructures consist of single crystalline GeS lateral bands (darker contrast in HAADF-STEM, Fig. 3(e and f)) around central regions with brighter contrast matching the shape of the initial SnS flake. TEM images of the central region (Fig. 3(g and h)) show the presence of stripe moiré patterns confirming the formation of vertically stacked GeS and SnS with aligned lattices along the [001] direction. Nanobeam electron diffraction confirms the vertical stacking of GeS and SnS in the central region of the flakes while a single-phase GeS diffraction pattern is observed in the lateral GeS band (Fig. S2, ESI†). Hence, the central region provides a van der Waals interface between the multilayer SnS flake and few-layer GeS, in addition to the covalent lateral interface between multilayer SnS and GeS at the periphery of the heterostructure. Raman spectroscopy of SnS–GeS multilayer heterostructures obtained with different GeS exposure during the second growth step illustrates the tunable thickness of the GeS across the top (001) facet of the flakes, i.e., the ability of obtaining morphologies ranging from structures covered by a thick (optically opaque) vertical GeS stack (Fig. S3(a–c), ESI†) to flakes with few-layer GeS coverage across the top facet (Fig. S3(d–f), ESI†).

The optoelectronics of homogeneous SnS flakes as well as the two types of heterostructures, with focus on the occupation of the two non-degenerate valleys along the Γ–X and Γ–Y directions in k-space (here referred to as X-valley and Y-valley), were interrogated by cathodoluminescence spectroscopy excited by the focused electron beam in STEM (STEM-CL). By using luminescence spectroscopy to probe light emission due to excited states at the two valleys, we can identify valley-selective carrier transfers across interfaces while avoiding the ambiguities inherent to other experiments, e.g., electrical transport measurements across the interfaces. Furthermore, the realization of large SnS flakes and heterostructures along with measurements with nanometer spatial resolution provides access to the properties of the van der Waals interfaces in the vertically stacked portion of the heterostructures. Flakes with sub-2 μm size readily support the excitation and propagation of photonic waveguide modes as well as interference phenomena involving the interaction of primary modes with guided modes reflected by the specular side facets (lateral waveguide modes).²⁵ The resulting interference fringes (see for example Fig. S4, ESI†), which hinder the analysis of luminescence spectra, can be avoided in STEM-CL measurements near the center of the large flakes and heterostructures prepared here.

The optoelectronic properties of (i) pure SnS flakes, (ii) SnS flakes whose (001) facets are terminated by few-layer SnS₂, and (iii) vertically stacked SnS–GeS heterostructures were thus probed by STEM-CL, using a focused (∼1–2 nm) electron beam as an excitation source and detecting the emitted light in the far field. Hyperspectral CL linescans were measured to demonstrate the uniformity of the spectra across the flake centers. STEM-CL measurements for a homogeneous SnS crystal are shown in Fig. 4. Fig. 4(a and b) show a HAADF-STEM image and a simultaneously acquired panchromatic CL map of a characteristic SnS flake. Fig. 4(c) shows a hyperspectral CL linescan that includes the edge region as well as the interior of the flake. An intensity modulation in dispersive fringes near the edge is rapidly attenuated toward the interior and becomes undetectable ∼0.8 μm from the flake edge. Spectra acquired at larger distances from the edge consistently show the same behavior, namely maxima in the emitted intensity at photon energies between 1.1–1.5 eV, as well as a broad peak at higher energy, centered at ∼1.8 eV (Fig. 4(d)). The high-energy emission, which originates from recombination between states far (>0.2 eV) from the band edges, is not relevant for the present discussion of the valleytronic properties of SnS crystals and SnS-based heterostructures. Hence, we focus the analysis on the low-energy region, which includes recombination across the X- and Y-valleys (see Fig. 1(b) and 5(a)). Using a Gaussian lineshape analysis, the band-edge luminescence can be deconvoluted into two narrow peaks (full width at half maximum, FWHM ∼ 0.10 to 0.15 eV) centered at 1.26 eV and 1.39 eV. These peaks are identified as corresponding to radiative transitions at the X-valley and Y-valley of SnS, respectively.^15,24 Note that the emission at 1.39 eV (Y-valley recombination) is significantly more intense than the peak at 1.26 eV (X-valley recombination), with a ratio of the peak areas (obtained from the Gaussian fits) of I^Y/I^X = 2.2.

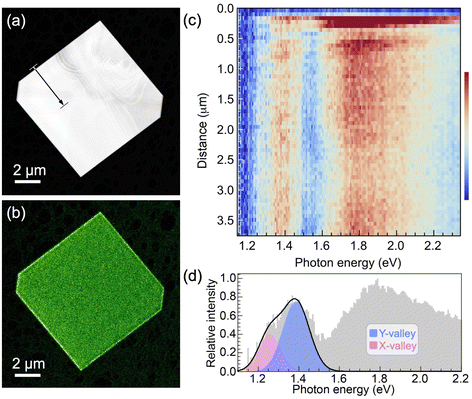Fig. 4 STEM cathodoluminescence spectroscopy of homogeneous SnS flakes. (a) HAADF-STEM image of a large, homogeneous SnS flake (edge length: 9.2 μm, thickness ∼150 nm; see Fig. S5 and S6, ESI†). (b) Panchromatic STEM-CL map of the flake shown in (a). (c) Hyperspectral CL linescan along the arrow in (a). (d) CL spectrum obtained within the SnS flake (>3 μm from the edge). Colored peaks: Gaussian lineshape analysis of the contributions of the SnS X-valley (pink) and Y-valley (blue) to the low-energy light emission.

Fig. 5 shows the band structures of all components of the vertical van der Waals heterostructures considered here, calculated using density functional theory (DFT; PBE-D2 with G₀W₀ quasiparticle corrections, see Methods).²⁴ The energy axes of the different band structures are aligned by calculating the electrostatic potential profiles from interface models of the vertical SnS–SnS₂ and SnS–GeS heterostructures (see Fig. S8, ESI†), so that they represent the actual band offsets between the van der Waals semiconductors. The interface models allowed us to determine the difference in the electrostatic potential (ΔV) across the van der Waals interface in each of the heterostructures, so that the valence band edges in the stacked crystals could be related to each other via the potential difference ΔV. Note that the calculations did not consider possible band bending. Such effects of interfacial charge transfer may play a role in the case of stacks of p-type SnS and n-type SnS₂, but for this system the band offsets are so large that our conclusions will not be affected. Band bending effects are expected to be small for vertical heterostructures between SnS and GeS (both the p-type semiconductors). Furthermore, due to their identical crystal structure and close chemical similarity, the calculations are expected to provide high accuracy in representing the band offsets between SnS and GeS.

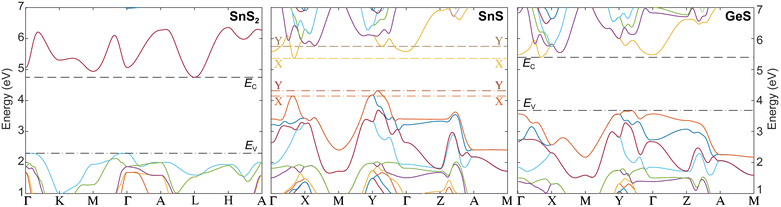Fig. 5 Energy-aligned band structures of SnS₂, SnS, and GeS, showing the different band offsets. The E(k) dispersion relations of the valence- and conduction bands of the three layered semiconductors were calculated using density functional theory with identical methodology (PBE-D2 with G₀W₀ quasiparticle corrections, see Methods) and their energy axes were aligned via the electrostatic potential from interface models of vertical SnS–SnS₂ and SnS–GeS van der Waals stacks (see Fig. S8, ESI†) to reflect the actual band offsets between the different valence- and conduction band extrema. Dashed and dash-dotted lines represent the conduction band minima (E_C) and valence band maxima (E_V), respectively. For SnS, the extrema at the X- and Y-valleys are indicated with brighter and darker colors, respectively. For an illustration of the Brillouin zones of the three crystals and designation of the high-symmetry points, see Fig. S7 (ESI†).

Fig. 6(a) shows a more detailed view of the band structure of SnS along the Γ–X and Γ–Y reciprocal space axes, illustrating the X- and Y-valleys. Fig. 6(b–e) summarize the structure and band diagrams (derived from the aligned band structures in Fig. 5) of the two types of heterostructures used for manipulating excited states at van der Waals interfaces. Fig. 6(b) illustrates the SnS–SnS₂ core–shell structures, in which a layered SnS core is surrounded by a wrap-around shell of few-layer SnS₂.¹⁶ The corresponding band diagram is shown in Fig. 6(c). The DFT-calculated alignment of the valence band maxima and conduction band minima between SnS and SnS₂ (Fig. 5 and 6(c)) is in good agreement with the measured band alignment reported in ref. 26, thus validating the calculations. The SnS–SnS₂ stack produces a type II (staggered) band alignment where the conduction band edge (E_C) in SnS₂ lies below E_C of both SnS valleys while the valence band edge (E_V) in the SnS X- and Y-valleys lies above E_V of SnS₂. This band alignment should cause the separation of near-interface electron–hole pairs excited in SnS, leading to the transfer of electrons across the interface into SnS₂ while the holes are retained in SnS. From the standpoint of valleytronics, this interface should not be of interest since the carrier transfer is not valley-selective, i.e., does not discriminate between the SnS X- and Y-valleys.

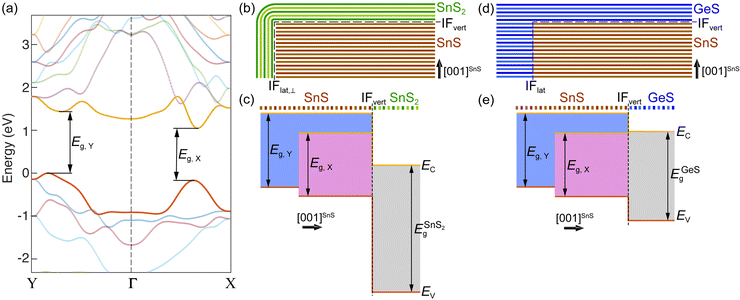Fig. 6 Band structure of SnS and band alignments in SnS-based heterostructures. (a) Detailed view of the SnS band structure (calculated with PBE-D2 G₀W₀, see Methods) along the Γ–X and Γ–Y directions in reciprocal space, showing the X- and Y-valleys. Bands straddling the bandgap are shown in red (valence band) and yellow (conduction band), respectively. (b) Schematic of an SnS–SnS₂ wrap-around core–shell heterostructure. (c) Band alignment between the two SnS valleys and the SnS₂ shell, as determined from the energy-aligned GW band structures of SnS and SnS₂ shown in Fig. 5. (d) Schematic of a layered SnS–GeS lateral/vertical heterostructure. (e) Band alignment between the two SnS valleys and the layered GeS cap, as determined from the energy-aligned GW band structures of SnS and GeS shown in Fig. 5.

A different situation is presented by the SnS–GeS heterostructure illustrated in Fig. 6(d). The alignment of the SnS X- and Y-valley band edges to the band edges in the GeS component of a SnS–GeS van der Waals stack was calculated by the same methodology used for computing the SnS–SnS₂ band offsets (see above), and the results agree well with previous calculations.²⁷ The band diagram across the vertical van der Waals interface (IF_vert) between SnS and GeS, shown in Fig. 6(e), indicates valley-specific interface types, namely a type I interface for the SnS X-valley and a type II interface for the Y-valley. While E_V for both SnS valleys lies above that of GeS (thus preventing the transfer of holes from SnS to GeS), the conduction band edge at the Y-valley lies above E_C in GeS (similar to the situation in SnS–SnS₂ discussed above). This type II band alignment will cause the separation of electron–hole pairs at the Y-valley. E_C of the X-valley, on the other hand, lies below E_C of GeS. The resulting type I band alignment is consistent with the retention of both electrons and holes at the X-valley of SnS. Overall, we therefore expect a quenching of the radiative recombination associated with the SnS Y-valley whereas the X-valley luminescence should remain high. The experimental confirmation of this scenario by luminescence spectroscopy would indicate the ability of selectively reading out the Y-valley population either optically or by other means, e.g., using electron transport across the SnS–GeS heterointerface.

Fig. 7 summarizes the results of STEM-CL measurements on the two types of SnS-based heterostructures. Fig. 7(a–c) represent spectroscopy on vertically stacked SnS and SnS₂, while Fig. 7(d–f) show our findings for van der Waals stacks of SnS and GeS. In both cases, measurements were conducted near the center of the flakes (see HAADF-STEM images, Fig. 7(a and d)) to probe only the effects of the vertical (van der Waals) interface and to exclude any influence from waveguide mode interference, as discussed above. Hyperspectral linescans, shown in Fig. 7(b and e), respectively, illustrate the reproducibility of the spectra across the central region of the heterostructures. Representative spectra (Fig. 7(c and f)) were used to perform a Gaussian lineshape analysis and deconvolute the low-energy peak into components due to the SnS X- and Y-valleys. Note that in both heterostructures, recombination across the fundamental bandgaps (E_g) of the top layers (SnS₂: E^ind_g = 2.25 eV;^28,29 GeS: E^dir_g = 1.65 eV)³⁰ lead to photon emission at substantially higher energies, i.e., do not affect the analysis of the low-energy emission at photon energies below 1.5 eV.

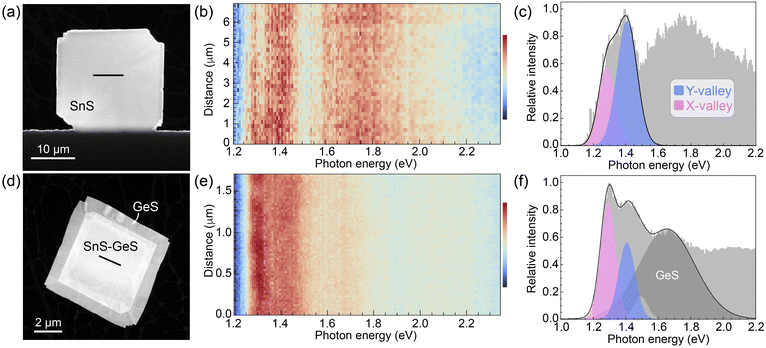Fig. 7 STEM cathodoluminescence spectroscopy of SnS-based heterostructures. (a) STEM image of an SnS–SnS₂ wrap-around heterostructure. (b) Hyperspectral CL linescan across the central part of the flake (line in (a); thickness ∼200 nm, see Fig. S5 and S6, ESI†). (c) Characteristic CL spectrum extracted from the linescan in (b). A Gaussian lineshape analysis shows two dominant components in the low-energy region corresponding to the X-valley (1.28 eV) and Y-valley (1.40 eV) emission in SnS, respectively. (d) STEM image of an SnS–GeS heterostructure. (e) Hyperspectral CL linescan across the vertically stacked central region of the SnS–GeS heterostructure (line in (d), thickness ∼140 nm, see Fig. S5 and S6, ESI†). (f) Characteristic CL spectrum extracted from the linescan in (e), along with a Gaussian lineshape analysis showing two dominant peaks stemming from the X-valley (1.29 eV) and Y-valley (1.40 eV) emission in SnS together with a third peak (centered at 1.65 eV), characteristic of the recombination across the fundamental bandgap of GeS.

The spectra of the SnS–SnS₂ heterostructures (Fig. 7(c)) appear similar to those of homogeneous SnS flakes (Fig. 4(d)), comprising a low-energy peak that can be deconvoluted into two components associated with the SnS X- and Y-valley, respectively. The ratio of the peak areas is I^Y/I^X = 1.9, i.e., the Y-valley emission remains substantially more intense than that of the X-valley. These findings are consistent with the realization of a type II interface between both SnS valleys and SnS₂, which is expected to cause equal carrier separation in the X- and Y-valleys (see Fig. 6(c)), leaving the emission intensity ratio from the two valleys unchanged from pure SnS flakes.

Spectra of SnS–GeS heterostructures (Fig. 7(f)) can also be deconvoluted into narrow low-energy peaks associated with the SnS X- and Y-valleys. In addition, there is a broader peak centered at 1.65 eV due to radiative recombination across the bandgap of GeS, and a minor component at ∼1.5 eV that is also detectable in homogeneous SnS (Fig. 4(d)). The major difference to SnS flakes and SnS–SnS₂ heterostructures is an inversion of the intensities of the two valleys, evident in the raw spectra. This is confirmed by a Gaussian lineshape analysis, which yields a ratio of the peak areas I^Y/I^X = 0.7, i.e., the intensity of the Y-valley emission is now smaller than that from the X-valley. This inversion of the Y/X intensity ratio is consistent with the expected valley-selective luminescence quenching due to the type II character for SnS^Y–GeS, and absence of carrier separation for SnS^X–GeS with type I band alignment (Fig. 6(e)).

Conclusions

We have used synthetic SnS flakes and SnS-based heterostructures to probe the potential for a valley-selective carrier transfer across van der Waals interfaces. Large flakes combined with electron-stimulated luminescence spectroscopy ensured measurements far from lateral flake edges, thus avoiding possible complications due to interference of edge-reflected photonic modes in the layered van der Waals crystals. Excitation at distances of several micrometers from edges and lateral interfaces ensured that any interface effects were due to vertically stacked portions of the heterostructures.

Spectroscopy on homogeneous SnS flakes shows a characteristic low-energy peak that can be deconvoluted into Gaussian components due to recombination at the X- and Y-valleys of SnS, with a reproducible intensity ratio I^Y/I^X = 2.2. A likely origin of this difference in emission are different joint densities of state (JDOS) for the X- and Y-valley. Indeed, the calculated band structure of SnS (Fig. 5 and 6(a)) shows larger band curvature (i.e., smaller effective mass, m*) for X-valley electrons and holes. Since the individual band DOS of a 3D semiconductor scales with 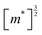, it follows that the valence- and conduction band DOS, and hence also the JDOS (proportional to 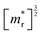, where 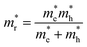is the reduced effective mass of electrons and holes) is larger for the Y-valley.

Vertically stacked SnS and SnS₂, expected to give rise to an interfacial type II band alignment for both valleys, preserves the overall spectral shape with a minor change in the I^Y/I^X ratio, consistent with a carrier extraction across the interface that does not discriminate between the two valleys. Vertical SnS–GeS heterostructures present a different situation, since they realize a type II alignment for the Y-valley but a type I alignment for the X-valley. For this system, we find a strong attenuation of the Y-valley emission leading to a reversal of the I^Y/I^X ratio to a new value of 0.7. Our combined results have important implications for unorthodox valleytronic systems such as SnS, with multiple non-degenerate and symmetry-distinct valleys. The findings demonstrate that suitable band offsets at heterointerfaces can be used for a valley-selective carrier extraction. In the present case, different alignments between the X- and Y-valley conduction band edges and the conduction band in GeS favored the transfer of Y-valley electrons from SnS to GeS. Given that the valence band edge of the X-valley lies below that of the Y-valley, the possibility exists that X-valley holes could be transferred selectively if a suitable heterostructure partner is identified. This raises the prospect of selectively reading out both the X-valley (holes) and Y-valley (electrons) via interfacial carrier transfers. Candidate materials for the selective readout of X-valley holes need to mirror the behavior at the SnS–GeS interface, namely: (i) their valence band maximum should fall between the valence band edges of the two SnS valleys to allow the selective transfer of X-valley holes; and (ii) their conduction band minimum should lie above the conduction band edges of both the X- and Y-valley of SnS to suppress the transfer of electrons from both valleys. Such a material, which may be identified by computational screening,³¹ could be integrated with the SnS–GeS stack reported here, for instance by van der Waals stacking on the free (001) facet of SnS.

We point out two additional conclusions that can be drawn based on the present experiments. Firstly, the fact that the valley intensity ratio is significantly modified in SnS–GeS heterostructures implies that the interfacial electron transfer must be quite efficient, even though the SnS flakes used here are fairly thick (∼150 nm, see Fig. S5 and S6, ESI†) and the required carrier transport is along the [001] direction, i.e., across the SnS van der Waals gaps. Thinner SnS flakes could further enhance the efficiency of the valley-selective electron extraction. And secondly, our data suggest that the rate of interfacial carrier transfer competes favorably with the rate of intervalley scattering, which might scramble the populations of the two SnS valleys. Hence, we conclude that intervalley scattering in this system will not impede the readout of the valley populations via carrier transfer.

Future challenges in the SnS valleytronics model system include (i) the realization of heterostructures with suitable band offsets in the valence and conduction bands to allow the readout of both the Y-valley occupancy (e.g., via electron transfer across a SnS–GeS junction, as demonstrated here) and the X-valley occupancy (via hole transfer across a suitable second interface, as suggested above); and (ii) the design of device architectures that enable the electrical readout of the valley states, building on the findings presented here. Overall, our results suggest that nontraditional valleytronic systems, such as the SnS-based van der Waals heterostructures analyzed here, may enable avenues for valley-selective readout of the carrier populations that avoid the complex topological effects required in transition metal dichalcogenides, instead relying on design parameters such as heterostructure band offsets that have long been established in semiconductor technology.

Materials and methods

Growth of SnS flakes on mica

Large multilayer SnS flakes were synthesized in a pumped quartz tube reactor with two independently controlled temperature zones. SnS powder (99.999%; ALB Materials) was used as the source material, purified by pre-annealing to 600 °C so as to release any excess sulfur that might be present in the original powder. The powder precursor was placed in a quartz boat in the center of the evaporation zone and heated to 600 °C. A freshly cleaved mica substrate (Ted Pella) was placed in the second temperature zone and heated to a growth temperature of 470 °C. During growth, an Ar (99.9999%, Matheson) carrier gas flow was maintained at 60 standard cubic centimeters per minute (sccm) and a pressure of 20 mTorr. Growth was typically performed for 20 minutes, after which the reactor was cooled naturally to room temperature.

Growth of SnS–SnS₂ heterostructures

SnS–SnS₂ wrap-around core–shell heterostructures were synthesized in a pumped quartz tube reactor with two independently controlled temperature zones, using an SnS₂ powder precursor (99.999%; ALB Materials) in the evaporation zone heated to 600 °C. A freshly cleaved mica substrate (Ted Pella), placed in the second zone, was heated to 470 °C. During growth, an Ar (99.9999%, Matheson) carrier gas flow was maintained at 60 sccm and a pressure of 20 mTorr. Growth was performed for 15 minutes, after which the reactor was cooled naturally to room temperature.

Growth of SnS–GeS heterostructures

SnS–GeS heterostructures were obtained by depositing GeS onto SnS seed flakes (synthesized as discussed above) via vapor transport using GeS powder (99.99%; ALB Materials) in a pumped quartz tube reactor with two temperature zones. The GeS precursor was placed in a quartz boat in the evaporation zone and heated to 420 °C. The zone containing SnS flakes on mica was heated to 320 °C. During growth, an Ar (99.9999%, Matheson) carrier gas flow was maintained at 60 sccm and a pressure of 76 Torr. GeS growth was typically performed for 15 minutes, after which the reactor was cooled naturally to room temperature.

Electron microscopy, nanobeam diffraction, and cathodoluminescence spectroscopy

Structure and morphology of the SnS flakes and SnS-based heterostructures were investigated by (scanning) transmission electron microscopy ((S)TEM) and nanobeam electron diffraction in an FEI Talos F200X field emission electron microscope. Cathodoluminescence spectroscopy was performed in STEM (STEM-CL) in a FEI Talos F200X microscope using a Gatan Vulcan CL holder at room temperature, 200 keV electron energy, and an incident beam current of ∼400 pA. Panchromatic CL maps (512 × 512 pixels, 1.28 ms per pixel) were acquired by scanning the exciting electron beam and recording the emitted light intensity at each pixel over a broad wavelength range (400–1000 nm). Hyperspectral linescans were acquired by displacing the electron beam in equal steps across individual flakes or heterostructures and acquiring full CL spectra (integration time: 10 s per spectrum) at each beam position.

Raman spectroscopy

Raman spectroscopy was performed using a Horiba Xplora Plus Raman microscope, a 100× objective, and 532 nm excitation wavelength at a laser power of 0.168 μW. Hyperspectral Raman linescans were obtained by scanning the focused laser in equal steps across the flakes and measuring full Raman spectra at each position (integration time: 10 s per spectrum).

Computational methods

All density-functional theory (DFT) calculations were carried out using the Vienna ab initio simulation package (VASP).^32,33 The structural relaxations were performed using the PBE-D2 functional^34,35 with 350 eV plane-wave cutoff. The GW calculations were carried out with the same parameters as in our previous study (ref. 24), where these parameters were carefully benchmarked. In particular, we consider the G₀W₀ flavor, the number of bands was set to 1280 and the k-point mesh to 16 × 16 × 3 for SnS and GeS. Since SnS₂ has only one layer in the primitive cell (as compared to two in SnS and GeS), the number of bands was reduced to 640 (resulting in about the same number of empty bands above the Fermi-level) and the k-point mesh was increased to 16 × 16 × 6. The Boltztrap2 software was used for interpolating the band structures.³⁶

The band alignments shown in Fig. 5 and 6 were obtained by calculating the electrostatic potential profile from an interface model of each of the heterostructures (SnS–SnS₂ and SnS–GeS; see Fig. S8, ESI†) and using these potential profiles to align the GW band structures via rigid shifts in energy. The electrostatic potential was evaluated at the atomic cores. Only interfaces in the out-of-plane (001) direction were considered. The heterostructure models were created to produce minimal strain (less than 1%) in both materials. The optimized lattice constants of the host materials are a = 4.0092 Å and b = 4.2664 Å for SnS; a = 4.0355 Å and b = 4.3402 Å for GeS; and a = 3.6850 Å and b = √3, a = 6.3826 Å for the tetragonal cell of SnS₂. For the SnS/GeS interface, we used an 11 × 1 cell (44.101 Å × 4.2664 Å) of SnS and a 12 × 1 cell of GeS (44.024 Å × 4.3402 Å), yielding maximal strain of about 0.2% and 1.7%. The supercell contains 6 layers of SnS and 6 layers of GeS (total of 552 atoms). The Brillouin zone was sampled using a 1 × 8 × 1 k-point mesh. The atom positions and all the lattice parameters were fully relaxed, after which the strain on each material was about half of the maximal strain and consequently the strain even in the b-direction dropped below 1%. For the SnS/SnS₂ interface, we used an 11 × 3 cell of SnS (44.101 Å × 12.799 Å) and a 12 × 2 cell of SnS₂ (44.220 Å × 12.765 Å), yielding maximal strain of about 0.3% and 0.3%. Due to the larger lateral size, the supercell was chosen to contain 4 layers of SnS and 4 layers of SnS₂ (total of 1104 atoms). The Brillouin zone was sampled using a 1 × 2 × 1 k-point mesh.

Data availability

The data that support the findings of this study are available in the ESI.†

Conflicts of interest

The authors declare no competing interests.

Acknowledgements

Research was sponsored by the Army Research Office and was accomplished under Award Number: W911NF-23-1-0060. The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the Army Research Office or the U.S. Government. The U.S. Government is authorized to reproduce and distribute reprints for Government purposes notwithstanding any copyright notation herein.

References

1. J. R. Schaibley, H. Yu, G. Clark, P. Rivera, J. S. Ross, K. L. Seyler, W. Yao and X. Xu, Nat. Rev. Mater., 2016, 1, 16055.
2. T. Cole, A. A. Lakhani and P. J. Stiles, Phys. Rev. Lett., 1977, 38, 722–725.
3. L. J. Sham, S. J. Allen, A. Kamgar and D. C. Tsui, Phys. Rev. Lett., 1978, 40, 472–475.
4. F. A. Zwanenburg, A. S. Dzurak, A. Morello, M. Y. Simmons, L. C. L. Hollenberg, G. Klimeck, S. Rogge, S. N. Coppersmith and M. A. Eriksson, Rev. Mod. Phys., 2013, 85, 961–1019.
5. K. F. Mak, K. He, J. Shan and T. F. Heinz, Nat. Nanotechnol., 2012, 7, 494–498.
6. H. Zeng, J. Dai, W. Yao, D. Xiao and X. Cui, Nat. Nanotechnol., 2012, 7, 490–493.
7. K. F. Mak, K. L. McGill, J. Park and P. L. McEuen, Science, 2014, 344, 1489–1492.
8. J. Lee, K. F. Mak and J. Shan, Nat. Nanotechnol., 2016, 11, 421–425.
9. D. Xiao, G.-B. Liu, W. Feng, X. Xu and W. Yao, Phys. Rev. Lett., 2012, 108, 196802.
10. A. Srivastava, M. Sidler, A. V. Allain, D. S. Lembke, A. Kis and A. Imamoğlu, Nat. Phys., 2015, 11, 141–147.
11. G. Aivazian, Z. Gong, A. M. Jones, R.-L. Chu, J. Yan, D. G. Mandrus, C. Zhang, D. Cobden, W. Yao and X. Xu, Nat. Phys., 2015, 11, 148–152.
12. D. MacNeill, C. Heikes, K. F. Mak, Z. Anderson, A. Kormányos, V. Zólyomi, J. Park and D. C. Ralph, Phys. Rev. Lett., 2015, 114, 037401.
13. L. C. Gomes and A. Carvalho, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 085406.
14. A. S. Rodin, L. C. Gomes, A. Carvalho and A. H. Castro Neto, Phys. Rev. B, 2016, 93, 045431.
15. S. Lin, A. Carvalho, S. Yan, R. Li, S. Kim, A. Rodin, L. Carvalho, E. M. Chan, X. Wang, A. H. Castro Neto and J. Yao, Nat. Commun., 2018, 9, 1455.
16. P. Sutter, J. Wang and E. Sutter, Adv. Mater., 2019, 31, 1902166.
17. E. Sutter, J. Wang and P. Sutter, ACS Nano, 2020, 14, 12248–12255.
18. E. Sutter, R. R. Unocic, J.-C. Idrobo and P. Sutter, Adv. Sci., 2022, 9, 2103830.
19. Y. Song, O. Chalaev and H. Dery, Phys. Rev. Lett., 2014, 113, 167201.
20. P. Sutter and E. Sutter, ACS Appl. Nano Mater., 2018, 1, 3026–3034.
21. T. Shimada, F. S. Ohuchi and B. A. Parkinson, J. Vac. Sci. Technol., A, 1992, 10, 539–542.
22. E. Sutter, J. Wang and P. Sutter, Chem. Mater., 2020, 32, 8034–8042.
23. Y. Huang, E. Sutter, J. T. Sadowski, M. Cotlet, O. L. A. Monti, D. A. Racke, M. R. Neupane, D. Wickramaratne, R. K. Lake, B. A. Parkinson and P. Sutter, ACS Nano, 2014, 8, 10743–10755.
24. P. Sutter, H.-P. Komsa, K. Kisslinger and E. Sutter, ACS Nano, 2023, 17, 9552–9564.
25. P. Sutter, C. Argyropoulos and E. Sutter, Nano Lett., 2018, 18, 4576–4583.
26. T. J. Whittles, L. A. Burton, J. M. Skelton, A. Walsh, T. D. Veal and V. R. Dhanak, Chem. Mater., 2016, 28, 3718–3726.
27. B. D. Malone and E. Kaxiras, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 245312.
28. L. A. Burton, T. J. Whittles, D. Hesp, W. M. Linhart, J. M. Skelton, B. Hou, R. F. Webster, G. O'Dowd, C. Reece, D. Cherns, D. J. Fermin, T. D. Veal, V. R. Dhanak and A. Walsh, J. Mater. Chem. A, 2016, 4, 1312–1318.
29. P. Sutter, H.-P. Komsa, A. V. Krasheninnikov, Y. Huang and E. Sutter, Appl. Phys. Lett., 2017, 111, 262102.
30. E. Sutter, B. Zhang, M. Sun and P. Sutter, ACS Nano, 2019, 13, 9352–9362.
31. L. Weston, H. Tailor, K. Krishnaswamy, L. Bjaalie and C. G. Van de Walle, Comput. Mater. Sci., 2018, 151, 174–180.
32. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
33. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
34. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
35. A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005.
36. G. K. H. Madsen, J. Carrete and M. J. Verstraete, Comput. Phys. Commun., 2018, 231, 140–145.

---

Footnote

† Electronic supplementary information (ESI) available: Supporting figures: Raman spectroscopy of SnS flakes, SnS–SnS₂ and SnS–GeS heterostructures; nanobeam electron diffraction analysis of SnS–GeS heterostructures; STEM imaging and STEM-CL panchromatic map and hyperspectral line scan of smaller SnS–GeS heterostructures; thickness analysis of SnS flakes and SnS-based heterostructures; Brillouin zones of SnS₂, SnS, and GeS. Interface models used for calculating band offsets in SnS–SnS₂ and SnS–GeS van der Waals heterostructures. See DOI: https://doi.org/10.1039/d4nh00231h

---