Active site engineering of intermetallic nanoparticles by the vapour–solid synthesis: carbon black supported nickel tellurides for hydrogen evolution

Abstract

The development and design of catalysts have become a major pillar of latest research efforts to make sustainable forms of energy generation accessible. The production of green hydrogen by electrocatalytic water splitting is dealt as one of the most promising ways to enable decarbonization. To make the hydrogen evolution reaction through electrocatalytic water splitting usable on a large scale, the development of highly-active catalysts with long-term stability and simple producibility is required. Recently, nickel tellurides were found to be an interesting alternative to noble-metal materials. Previous publications dealt with individual nickel telluride species of certain compositions due to the lack of broadly applicable synthesis strategies. For the first time, in this work the preparation of carbon black supported nickel telluride nanoparticles and their catalytic performance for the electrocatalytic hydrogen evolution reaction in alkaline media is presented. The facile vapour–solid synthesis strategy enabled remarkable control over the crystal structure and composition, demonstrating interesting opportunities of active site engineering. Both single- and multi-phase samples containing the Ni–Te compounds Ni₃Te₂, NiTe, NiTe_2−x & NiTe₂ were prepared. Onset potentials and overpotentials of −0.145 V vs. RHE and 315 mV at 10 mA cm⁻² respectively were achieved. Furthermore, it was found that the mass activity was dependent on the structure and composition of the nickel tellurides following the particular order: Ni₃Te₂ > NiTe > NiTe_2−x > NiTe₂.

---

Introduction

Due to the rise in global population and development of the economy, the global energy demand is expected to remain steadily increasing. To the largest extent, fossil fuels such as oil, coal and natural gas are used for power generation.¹ The adverse impact on the environment as well as the depletion from non-renewable fossil fuels stimulates the research in innovative technologies for clean and sustainable energy conversion and storage. Future energy carriers must have a low environmental impact and should be renewable and easily accessible; they must have a high energy density and be prone to an efficient energy conversion.²

Hydrogen is expected to be one of the most promising and potent energy carriers to tackle the challenges of climate crisis and substitute fossil fuels.^3,4 Hydrogen offers versatile options of implementation in sustainable future scenarios.⁵ A high gravimetric energy density of 120 MJ kg⁻¹ and eminent abundance make hydrogen suitable for efficient energy storage.⁶ Among the most promising technologies for clean hydrogen production, electro-catalytic water splitting powered by solar, or wind power has been the centre of attention for decades.^7–9 Water electrolysis involves the two half-cell reactions: hydrogen evolution (HER) on the cathode side, with simultaneous oxygen evolution (OER) on the anode side (Fig. 1).

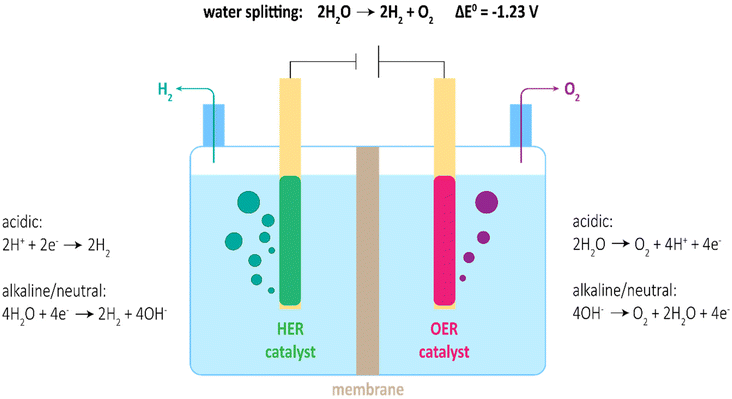Fig. 1 Scheme of water electrolyser with respective half-cell reactions in acidic, alkaline, and neutral media.

Unfortunately, both reactions, but in particular OER, are hindered by sluggish reaction kinetics, demanding for high overpotentials to achieve reasonable current densities. Thus, input potentials of practical water electrolysers are much larger than the theoretical 1.23 V, ultimately leading to low energy conversion efficiencies.¹⁰ To perform water splitting with acceptable efficiency, sophisticated electrocatalysts are needed. State-of-the-Art catalysts involve noble metal-based materials (e.g. Pt, IrO₂ and RuO₂) for acidic media and transition metal-based materials (e.g. Ni, Fe and Co) for alkaline media.^9,11 Though, high cost and unsatisfactory catalytic stability of noble metal-based catalysts as well as moderate activity of transition metal-based catalysts yet hinder the broad application of water splitting for industrial-scale H₂ production. Hence, realization of large-scale H₂ production by water splitting requires the development of competitive non-noble electrocatalysts. On account of favoured thermodynamics for OER in alkaline media, potential catalysts for HER should also be optimised for alkaline media to allow reconcilable implementation.

Recently, “active site engineering”, in which the accessibility, reactivity and density of catalytically active sites should be controlled through optimized synthesis approaches, became the significant strategy for catalyst development.¹² Latest research focusses on the idea of morphology and electronic structure tuning.^13,14 Morphology tuning strategies target the formation of 2D and highly dispersed 3D materials (e.g. nanoparticles). Those materials have higher specific surface areas and porosities, therefore an increase in accessibility of active sites compared to planar bulk materials is achieved. Electronic structure tuning on the other hand utilises the possibility to alter the electronic structure and form active sites through vacancy engineering, elemental doping, or control over crystal phase formation.

Following these developments, intermetallic compounds moved into the spotlight of researchers.¹⁵ Intermetallic compounds consist of two or more (transition-)metals arranged in crystal structures differing from their constituting metals (e.g. transition metal chalcogenides). In the intermetallic compounds a mixture of metallic, covalent, and ionic bond contents leads to unique physical, chemical, and mechanical characteristics.¹⁶ Long-range order, high stability and designability of morphology and electronic structure make intermetallic compounds ideal catalyst materials.¹⁷ Although their excelling catalytic performance is well documented, synthesis of intermetallic compounds, particularly in nanoparticle shape remains challenging.¹⁸

Synthesis methods of intermetallic nanoparticles can typically be divided into the two categories of thermal annealing and wet-chemistry approaches.¹⁹ For thermal annealing routes, thermodynamic and kinetic studies imply that disordered alloys exist in a meta-stable state relative to the well-ordered intermetallic phase. When the alloy is annealed at elevated temperatures the atoms will arrange in the highly ordered intermetallic structure.²⁰ Unfortunately, the high temperatures needed to overcome the kinetic energy barriers promote particle aggregation, sintering and Ostwald ripening. In wet-chemistry methods, on the other hand, co-reduction of dissolved precursors is carried out in the presence of stabilizers, capping- and reduction agents at milder temperatures. The need for various additives not only limits the product quality but also enforces difficult individual synthesis development for each intermetallic system, limiting their comparability and hindering their broad usage.²¹

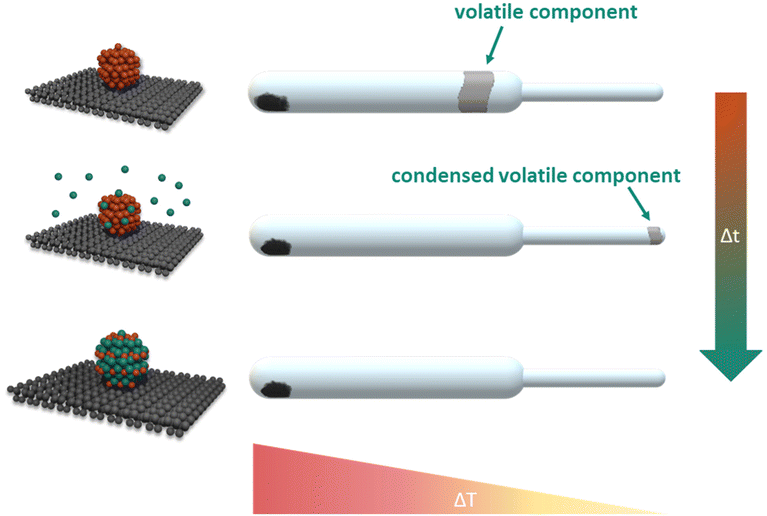
A preeminent response to the above-mentioned synthesis challenges is the facile, direct vapour–solid (VS) synthesis method. The vapour–solid synthesis emerged from the isopiestic method and was originally developed for the stoichiometric preparation and study of intermetallic bulk compounds.^22,23 Subsequently, supported intermetallic nanoparticles moved into the focus of research effort in our group.^24,25 For the preparation of intermetallic compounds by the vapour–solid approach, stoichiometric amounts of the constituting metals are sealed in an evacuated quartz vessel, separated in space and equilibrated within an temperature gradient. The reaction partner with lower vapour pressure condenses on the coolest part of the system. From the respective temperature the system pressure and consequently the activity are controlled (Fig. 2). The absence of any additives, use of simple, commercially available educts with high purity and the excellent compositional control enables the synthesis of various intermetallic compounds with morphological and electronic structure tunability.

Fig. 2 Schematic illustration of the vapour–solid synthesis method.

Nickel-based materials can offer highly active and stable alternatives to state-of-the-art catalysts.²⁶ A comparison between representative nickel chalcogenide materials and their reported overpotential at 10 mA cm⁻² are presented in Table 1. In particular Nickel-tellurides unveiled outstanding electrocatalytic performance for HER in recent publications.^27–41

Table 1 Representative nickel-based catalysts and their HER performance in 1 M KOH

Catalyst and morphology	Supports	Loading [mg cm^−2]	η 10 [mV]	References
NiTe2 nanowire	Nickel foam	1.98	113	Anantharaj et al.^29
NiSe nanowire	Nickel foam	21.47	135	Ren et al.^42
Ni3S2 nanowire	Nickel foam	19.28	123	Ren et al.^42

---

Nonetheless, the research field lacks a broadly applicable synthesis strategy capable of distinct and composition-controlled preparation. To the best of our knowledge, this is the first time the synthesis of carbon black supported nickel telluride nanoparticles and their performance in electrocatalytic HER are reported. In this work we aim to present the direct vapour–solid method to a wide audience and highlight its potential in future catalyst development by benchmarking carbon black supported, single- and multiphase nickel telluride nanoparticles for electrocatalytic HER in alkaline medium. An overview about the intermetallic nickel–tellurium system⁴³ from bulk studies is presented in Table 2.

Table 2 Crystallographic and phase diagram information for the nickel–tellurium system

Name	Formula	Structure type	Space group	Homogeneity range^43 [at% Te]	Lattice parameters [nm]	References
(Ni)	Ni	Cu	Fm3̄m	—	a = 3.5181	P. Juhás et al.^44
β2	Ni3+xTe2	Own type	P121/m1	41–42	a = 0.3376	J. Barstard et al.^45
					b = 0.3800
					c = 0.6100
					β = 91.25°
γ1	NiTe0.775	Own type	Pmc21	—	a = 0.3916	K. Klepp et al.^46
					b = 0.6860
					c = 1.232
δ	NiTe2−x	NiAs	P63/mmc	51–67	a = 0.3956	J. Barstard et al.^45
					c = 0.5370

---

Experimental section

Chemicals

Nickel(II) acetylacetonate, for synthesis (Merck, Germany); carbon powder, steam activated & acid washed, Norit GSX (Alfa Aesar, Germany); platinum on carbon, 10 wt% (Sigma-Aldrich, Germany); ethanol, 96% (Brenntag, Austria); Nafion®-117, around 5% in a mixture of water and lower aliphatic alcohols (Sigma-Aldrich, Germany); KOH pellets, 85% (VWR Chemicals, Germany); 2-propanol ≥99.5% (Sigma-Aldrich, Germany); Al₂O₃ MicroPolish suspension, 0.05 μm and 1 μm (Buehler Ltd, Germany); tellurium, 99.99+% (ASARCO; United States of America); Tellurium AAS-standard solution, 1000 mg L⁻¹ Te in 2% HNO₃ (Carl Roth, Germany); nitric acid, 69% HNO₃ suprapur (Merck, Germany); Inoxline H5, 95 vol% Ar/5 vol% H₂ (Messer, Austria); Hydrogen 5.0, 99.999% H₂ (Messer, Austria); Argon 5.0, 99.999% Ar (Messer, Austria).

All chemicals were used as purchased. Water was purified and deionized (18.2 MΩ cm) in-house by a Milli-Q® (Merck, Germany) system.

Preparation of Ni/C

Synthesis of the carbon supported nickel nanoparticles was carried out by a facile wet impregnation – thermal decomposition method similar to the procedure described by Schubert et al.⁴⁷ In a 250 mL round-bottomed flask, the nickel(II) acetylacetonate precursor was diluted in about 50 mL of ethanol. The respective amount of carbon powder was added and dispersed by 15 minutes of sonification. The solvent was removed under reduced pressure and constant stirring at 40 °C. The wet powder was dried at 95 °C under ambient atmosphere for 15 minutes and subsequently calcinated at 350 °C for 10 h. Reduction of the material was carried out in a tube furnace (Nabertherm, Germany) at 350 °C in an Inoxline (Ar/H₂ = 95/5 = v/v) gas stream of about 30 mL_N min⁻¹ for 2 h. Afterwards, the gases were removed at 350 °C for 2 h under reduced pressure. The as-prepared Ni/C powder was transferred and stored in argon atmosphere.

Preparation of Ni–Te/C by the vapour–solid approach

Pure tellurium was weighed to an accuracy of ±0.1 mg and transferred into a custom-built quartz glass tube. The quartz glass tube was connected to a vacuum line and put under reduced pressure of ≤2 × 10⁻² mbar. The tellurium was evaporated under static conditions by heating the tube with a H₂/O₂-torch and consequently condensed as a thin layer on the cool, top side of the quartz glass tube. The evacuated tube was moved into a glovebox (MBraun, Germany) with argon atmosphere. The respective amount of Ni/C powder was transferred into the quartz glass tube without direct contact to the tellurium layer using a funnel and a pipe cleaner. The quartz glass tube, with the Ni/C powder on the bottom and the tellurium layer on top, was mounted on the vacuum line under argon atmosphere and then alternately evacuated and purged with argon. Finally, the quartz glass tube was sealed above the tellurium layer under reduced pressure of ≤2 × 10⁻² mbar. The evacuated vessel was transferred into a two-zone furnace (HTM Reetz, Germany) and aligned in a temperature gradient of 422 °C at the tellurium side and 448 °C at the Ni/C side of the final experimental setup. The reaction progress was monitored by the fading and ultimately disappearance of the condensed tellurium. Full conversion was earliest observed after 1 day of reaction. To ensure homogeneity of the samples, an isothermal post-reaction step of 1 to 3 days at 400 °C in a muffle furnace (Nabertherm, Germany) was applied to the reaction vessels. The reaction vessels were opened in the glovebox and the produced Ni–Te/C catalysts were stored under argon.

Materials characterization

Quantitative analysis of the materials was done by Total X-ray fluorescence spectroscopy with a Picofox S2 (Bruker, Germany) setup. About 30 mg of the respective catalyst powders were dispersed in 20 mL of 2 mol L⁻¹ HNO₃ and kept under constant stirring at 105 °C for one hour. Subsequently, the dispersions were filtered, and the solutions each diluted up to 100 mL with ultra-pure water. In 1.5 mL Eppendorf tubes, 500 μL of the respective solutions were mixed with 500 μL of 30 mg L⁻¹ Ga standard solution and 100 μL of 0.3 g L⁻¹ polyvinyl alcohol solution. For analysis 5 μL of the sample solutions were transferred onto quartz plates and dried under infra-red irradiation and reduced pressure for 45 minutes. The dried plates were mounted to the Picofox S2 apparatus and measured for 400 seconds each. Gain correction was carried out with an arsenic standard mounted on a quartz sample holder. For quality control 10 mg L⁻¹ Ni and 10 mg L⁻¹ Te standard solutions were as well measured using 30 mg L⁻¹ Ga is internal standard.

Phase composition and structural information of the catalysts was acquired by powder X-ray diffraction with a D8 Advance (Bruker, Germany) diffractometer in Bragg–Brentano pseudo focusing mode with theta/theta geometry and structure refinement with the Topas 7.13 software. Zero-background silicon single-crystal plates covered with a thin layer of grease to fix the powders were used as sample holders. For all measurements, the diffractometer was mounted with a one-dimensional silicon strip detector, Lynxeye (Bruker, Germany). Patterns were determined in the 30° to 90° 2-theta range over 3 h with an acceleration voltage of 40 kV and a beam current of 40 mA.

Nitrogen adsorption–desorption isotherms were recorded at −196 °C with a QuantaTech Inc. iQ3 (Anton Paar, USA) physisorption setup. Outgassing was performed at 80 °C for 12 h. The Anton Paar QuantaTech Inc. ASiQWin 5.2 software was used for data evaluation. The Brunauer–Emmett–Teller (BET) equation was applied to calculate the specific surface area (SSA) in the relative pressure range of 0.05–0.20 P/P₀. For comparison, the specific surface area and the pore size distribution were also determined according to the quenched solid density functional theory (QSDFT) from the adsorption branch of the isotherms, which is reported to result in more precise values for carbon materials.^48–50 For the QSDFT calculations, slit/cylindrical pore geometries of carbon were assumed. Based on the Gurvich rule, the total pore volume was evaluated at the plateau region of the isotherm at P/P₀ = 0.95.

Electron microscopy was carried out for size verification of the intermetallic nanoparticles as well as elemental mapping. The scanning and high-resolution images were taken at a Talos F200i (Thermo Scientific™, Germany) transmission electron microscope (TEM) operated at a voltage of 200 kV, equipped with a field electron gun (FEG) and a 4k·4k Ceta 16M camera. Data evaluation was done in Velox software.

Electrochemical measurements

Benchmarking the materials regarding their electrocatalytic HER performance and stability in alkaline media was carried out according to recently recommended practices.^51–53 All investigations were conducted in a quartz glass cell using a PGSTAT302N Autolab electrochemical workstation (Metrohm, Germany). The cell was filled with 200 mL of 1.0 M KOH (VWR pellets dissolved in ultra-pure water) and kept at a constant temperature of 30 °C by an external thermostat. Prior to the measurement, the electrolyte solution was purged with argon gas for 30 minutes. In a typical three-electrode setup, a graphite rod, a HydroFlex reversible hydrogen electrode (Gaskatel, Germany), and a glassy carbon rotating disc electrode (GC-RDE) with a disc area of 0.196 cm² (Metrohm, Germany) modified with the catalyst material were used as counter, reference, and working electrode respectively.

The catalyst suspension was prepared by dispersing 4.8 mg of the catalyst powder in a mixture of 700 μL ultra-pure water, 250 μL 2-propanol, and 50 μL Nafion® solution and subsequent sonication for 15 minutes. The GC-RDE was polished over Polish cloth with 1 μm and 0.05 μm Al₂O₃ suspension to give a mirror finish and subsequently sonicated in ultra-pure water for 5 minutes. 10 μl of the freshly prepared catalyst suspension were drop-cast onto the polished electrode disc and dried under light irradiation for 30 minutes. The preparation led to a final catalyst loading of the working electrode of 0.24 mg cm⁻².

All electrochemical measurements were recorded at a RDE rotation speed of 1600 rpm. For the cyclic voltammetry (CV) and linear sweep voltammetry (LSV) measurements, 90% of the iR-drop was corrected by the Nova 2.1.5 software (Metrohm, Germany). To ensure reproducibility, the measurements were repeated in triplicates. For data evaluation the measurement closest to the median values was chosen. Prior to the catalyst screening, the open circuit potential (OCP) was screened for at least six minutes, the electrode was accepted as stable if potential changes of ≤10 mV s⁻¹ were achieved for the last minute of measurement.

The working electrode was activated by a series of CV measurements under constant argon purging of the electrolyte: alternately, in the potential range of 0.4 to −0.4 V vs. RHE, 1 cycle with a scan rate of 10 mV s⁻¹ was followed by 25 cycles with a scan rate of 100 mV s⁻¹ until 53 activation cycles were recorded in total. Potentiostatic electrochemical impedance spectroscopy (EIS) in a range from 100 kHz to 100 mHz with an amplitude of 5 mV at an applied potential of −0.3 V vs. RHE, allowed for further investigation of the catalyst's reaction kinetics. The electrochemical active surface area (ECSA) was assessed similar as described by McCrory et al.¹¹ by investigating the double layer capacitance: CVs with ascending scan rates (20 to 220 mV s⁻¹, 5 cycles per scan speed) in the non-faradaic current region (0.05–0.15 V vs. RHE) were measured. The respective anodic and cathodic current values at 0.10 V vs. RHE were plotted over the scan rate. The determined double-layer capacitance (C_DL) of the system was taken as the average of the absolute values of the slope of the linear fits to the data. The specific capacitance (C_S) reference value of 0.040 mF cm⁻², which was reported to be a typical approximation in alkaline media, was used to estimate the ECSA as the product of C_DL·C_S⁻¹.³⁴

To exclude the impact of hydrogen formation during the reaction, the LSV measurements, in the potential range of 0.4 to −0.4 V vs. RHE, were recorded after purging the electrolyte with hydrogen gas for 30 minutes.

Catalyst stability was investigated by chronoamperometric (CA) measurements in argon purged electrolyte over 12 h at a constant potential of −0.25 V vs. RHE. Before and after the CA measurement a LSV curve was recorded and each 500 μL of the electrolyte solution were taken for TXRF spectroscopy investigation.

Results and discussion

X-ray fluorescence spectroscopy

The elemental compositions of the supported nickel educts and the supported intermetallic powders were analysed using Total X-ray fluorescence spectroscopy (TXRF). Measured concentrations for Ni standard solution were within a 95% confidence interval of the nominal concentration and the results for all samples were used without any further correction. Recovery rate experiments with a 10 mg L⁻¹ Te standard solution showed, that a correction factor of 0.45 for the tellurium concentrations had to be applied for the samples under used conditions (Table S1†). The results for samples are presented based on the total powder mass (Table 2 & S2†). Product compositions deviate within the range of a few percent points to the targeted concentrations. Also, it is observed that the deviations found for both Ni and Te mostly behave coherent, indicating cause by balancing variations. Overall, quantification of the powders highlights the superior composition control of the vapour–solid synthesis method.

In addition, TXRF was used to investigate the electrolyte solution used for electrocatalytic tests. Typical limits of detection are in the low ppb range. The spectra did not show any Ni, Te, or Fe impurities prior to catalytic testing, nor after the twelve hours lasting chronoamperometric measurements.

X-ray diffraction and Rietveld refinement

Generally, structural characterization of supported nanoparticles is a challenge, as the small particles cause broad reflections and those may overlap with the patterns of crystalline support materials. The carbon black starting material was investigated by PXRD both, before and after, the respective conditions of annealing and reduction which are applied to the material during the synthesis of the metallic nanoparticles. No severe differences were observed between the carbon black material before and after annealing and reduction. The pattern revealed mainly amorphous behaviour with some minor reflections. Since the pattern could not solely be described with the graphite structure (graphite-type, P6₃/mmc),⁵⁴ the description was augmented empirically by inserting 14 reflections and is referred to as “simulated support”. The individually refined reflection positions, profile function and scaling factors yielded a satisfactory fit to the observed pattern of the support. The measured and refined powder diffraction patterns of the Ni/C powder as well as of two representative Ni–Te/C sample are shown in Fig. 3 respectively. Other patterns are presented in Fig. S1.† The expected crystal structures include Ni (Cu-type, Fm3̄m),⁴⁴ NiO (NaCl-type, Fm3̄m),⁵⁵ Ni_3+xTe₂ (Ni₃Te₂-type, P12₁/m1),⁵⁶ NiTe_0.775 (Pmc2₁)⁵⁶ and NiTe_2−x (NiAs-type, P6₃/mmc).⁴⁶ Except for the stoichiometric compound NiTe_0.775, all mentioned compounds were successfully verified. Rietveld refinement, including the empirical description simulating the carbon black support, resulted in individual crystallographic parameters for the various phases in the samples listed in Table 4.

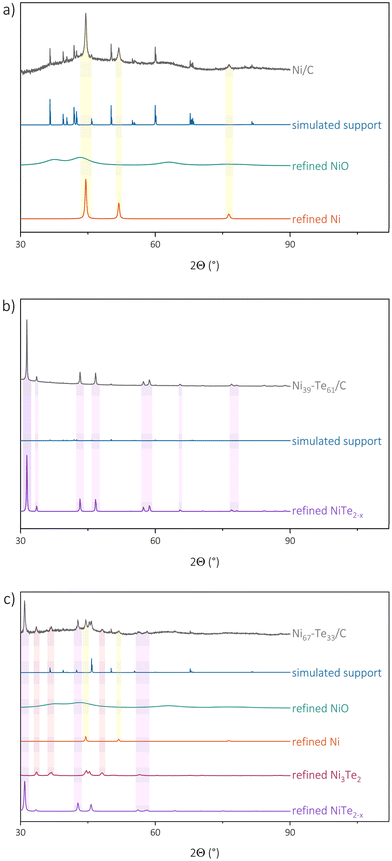Fig. 3 Measured and refined pXRD patterns with the most significant peaks highlighted of Ni/C (a), Ni₃₉–Te₆₁/C (b) and Ni₆₇–Te₃₃/C (c).

Table 3 TXRF results of the intermetallic products

Sample	ω TXRF(Ni) [wt%]	ω target(Ni) [wt%]	ω TXRF(Te) [wt%]	ω target(Te) [wt%]
Ni85–Te15/C	17.6	15.2	6.0	5.8
Ni78–Te22/C	19.6	19.5	8.8	11.9
Ni67–Te33/C	9.6	6.7	9.4	7.2
Ni60–Te40/C	8.6	6.5	10.6	9.5
Ni49–Te51/C	15.6	11.8	28.7	26.9
Ni39–Te61/C	12.3	10.5	39.8	35.0

---

Table 4 Lattice parameters and the calculated volume weighted mean column height (LVol-FWHM, Lorentzian Volume full width at half maximum) obtained from Rietveld refinements of Ni/C and Ni–Te/C samples

Sample	Phase	Lattice parameters [Å]	LVol-FWHM [nm]
a LVol-FWHM value not observed due to overlapping composition sets of the same phase.
Ni/C	Ni	a = 3.529(9)	27.(9)
	NiO	a = 4.177(0)	1.(2)
Ni85–Te15/C	Ni	a = 3.528(7)	45.(1)
	NiO	a = 4.177(0)	1.(0)
	NiTe2−x	a = 3.939(2)–3.975(2), c = 5.321(5)–5.368(1)
Ni78–Te22/C	Ni	a = 3.529(3)	37.(0)
	NiO	a = 4.177(0)	4.(0)
	NiTe2−x	a = 3.874(3)–3.963(7), c = 5.329(2)–5.372(0)
Ni67–Te33/C	Ni	a = 3.531(3)	54.(8)
	NiO	a = 4.177(0)	1.(3)
	NiTe2−x	a = 3.977(4), c = 5.368(2)	36.(1)
	Ni3Te2	a = 7.592(2), b = 3.777(1), c = 6.142(5)	26.(2)
Ni60–Te40/C	Ni	a = 3.530(5)	47.(2)
	NiO	a = 4.177(0)	1.(2)
	NiTe2−x	a = 3.948(8)–3.975(5), c = 5.369(2)–5.371(2)
	Ni3Te2	a = 7.586(3), b = 3.770(3), c = 6.136(3)	22.(9)
Ni49–Te51/C	NiO	a = 4.177(0)	1.(3)
	NiTe2−x	a = 3.902(7)–3.953(0), c = 5.356(1)–5.369(6)
Ni39–Te61/C	NiO	a = 4.177(0)	1.(2)
	NiTe2−x	a = 3.889(7), c = 5.340(1)	89.(0)

---

Surprisingly, NiTe_2−x was present in all samples. Furthermore, it was observed that peak-broadening occurred for those NiTe_2−x patterns of samples, which were not targeting the NiTe_2−x phase region directly. The peak-broadening is caused by the presence of slightly differing lattice parameter sets reflecting compositional variations, hence hinting that those samples were not finally in thermodynamic equilibrium. Furthermore, the peak broadening hinders an explicit evaluation of the crystal domain size of NiTe_2−x in the sample. The NiAs structure type of the NiTe_2−x phase has a broad, potential homogeneity range and would allow for intermetallic Ni–Te compositions to extend from Ni₂Te to NiTe to NiTe₂, dependent on the occupation of vacancies and interstitial sites.⁵⁷ The lattice parameter ‘a’ is increasing with decreasing tellurium concentration in NiTe_2−x.⁴³ For nanoparticles, the phase stability is greatly dependent on morphology and size. A homogeneity range, and the associated flexibility regarding composition and activity, could therefore benefit the stability of such phases compared to stoichiometric line compounds like NiTe_0.775. Another factor of this behaviour might be that simpler and comparatively smaller structures are more facile to form in nanoparticles contrary to complex structures with high unit cell volume. Our observations indicate that NiTe_2−x is the most favourable structure formed from our starting material.

Rietveld refinement confirmed vacancy formation on the nickel sites in samples with high tellurium concentration, while the nickel doping on interstitial sites could not be seen. This led to a composition of NiTe_1.9 and NiTe_1.8 for phase-pure catalysts. In samples which were not in equilibrium (e.g. Ni₈₅Te₁₅/C & Ni₇₈Te₂₂/C), NiTe was the dominant NiTe_2−x composition. A slight shift towards higher tellurium concentration is caused by partial oxidation of nickel reflected by the observation of almost amorphous NiO in the patterns.

Transmission electron microscopy and energy dispersive X-ray spectroscopy

Transmission electron microscopy (TEM) images were taken from the as-prepared Ni/C educt material as well as the intermetallic Ni–Te/C catalyst products. Exemplary bright field images of Ni₃₉–Te₆₁/C are presented in Fig. 4. The TEM images show that the carbon surface was loaded with dispersed, randomly oriented, edgy nanoparticles. While the particles of the intermetallic products were evenly dispersed, the Ni/C educt exhibited agglomerated areas of smaller particles besides the well dispersed bigger particles.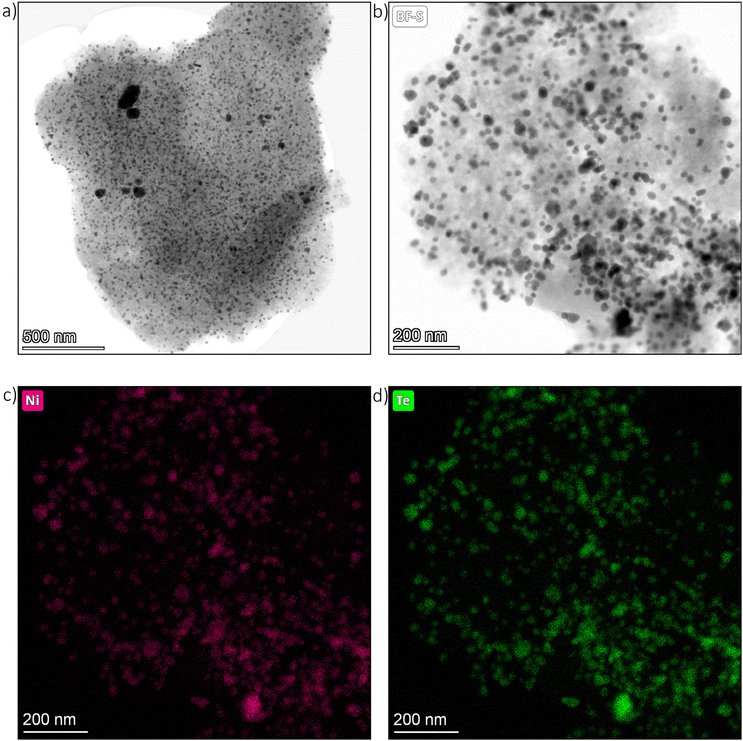

Fig. 4 TEM images of Ni₃₉–Te₆₁/C particle (a) & (b) as well as respective nickel (c) and tellurium (d) elemental maps.

Energy dispersive X-ray spectroscopy (EDS) confirmed the expected nanoparticle compositions. The nickel nanoparticles of the Ni/C educt were at least superficially oxidized in contact to air, confirming the necessity of pre-reduction and handling under inert atmosphere for the vapour–solid reactions. Selective tellurium intake into the nickel nanoparticles was assured by EDS elemental mapping of the intermetallic Ni–Te/C catalyst powders (Fig. 4).

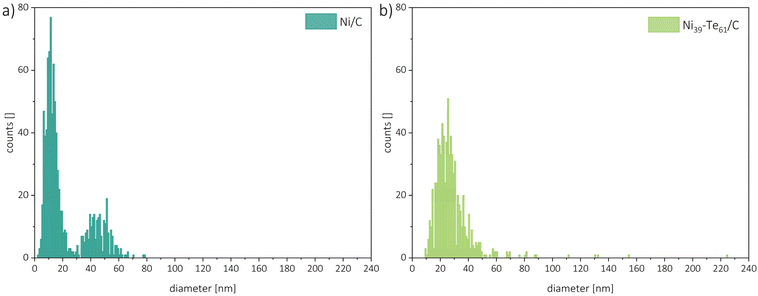
For particle size analysis, the diameters of about 400 particles per sample were measured in both the horizontal and vertical directions. To minimize the impact of outliers, several powder particles were compared. Representative particle size distributions are shown in Fig. 5. The Ni/C educt displayed a bimodal particle size distribution with estimated diameters of 11 nm and 45 nm, with the smaller particles being the dominant species. The intermetallic Ni–Te/C catalyst powders, on the other hand, showed a more uniform particle size distribution which was shifted slightly in comparison to the educt pattern towards bigger particle sizes. Thus, hinting on the agglomeration and sintering of the small, accumulated nickel particles during the formation of the intermetallic compound. As expected, a higher tellurium concentration leads to the increase of particle size. Very rarely single particles of sizes up to 225 nm were observed in the intermetallic products.

Fig. 5 Particle size distributions of Ni/C (a) and Ni₃₉–Te₆₁/C (b).

Physisorption

The nitrogen adsorption–desorption isotherms of the carbon black supported materials were measured at −196 °C and show a typical type IV isotherm for mesoporous carbon materials. The isotherms and resulting QSDFT pore size distributions are plotted in staggered form to prevent overlapping of the curves in Fig. S3.† According to IUPAC standards⁵⁸ the broad hysteresis loops, observed from 0.45 up to 0.95 P/P₀ can be classified as H4 type. H4 type materials are typically associated with non-rigid aggregates of plate-like particles leading to slit-shaped pores including micropores.⁵⁹ The desorption branch of the isotherm closes the hysteresis loop at around 0.40–0.45 P/P₀, which is due to the cavitation effect and does not reflect a true pore size but rather an artefact.⁵⁰ Therefore, the adsorption branch was used for data evaluation. A slight difference in the high relative pressure regime between the commercial Pt/C and the in-house prepared catalysts is caused by the different carbon support materials. The nickel and nickel telluride loadings only slightly affect the porosity of the material. Hence, it is concluded that the (inter-)metallic nanoparticles are loaded at the surface of the support.

QSDFT calculations performed on the adsorption branch of the isotherm and assuming slit/cylindrical pore geometries of carbon, revealed the presence of micropores in all samples. The average micropore volume, total pore volume and specific surface areas are presented in Table 5. Comparison of the calculated QSDFT and BET specific surface areas lead to comparable values and an expected trend of decreasing surface areas with increasing (inter-)metallic content. The significantly higher surface areas of the samples Ni₆₇–Te₃₃/C and Ni₆₀–Te₄₀/C results from the comparably lower initial metal loading of the respective educt batch.

Table 5 BET specific surface areas, QSDFT calculated specific surface areas, total and micropore volumes

Sample	S BET [m^2 g^−1]	S DFT [m^2 g^−1]	V tot [cm^3 g^−1]	V micro [cm^3 g^−1]
Pt/C	1198	992	0.84	0.25
C	736	760	0.65	0.21
Ni/C	662	622	0.60	0.15
Ni85–Te15/C	483	452	0.42	0.12
Ni78–Te22/C	440	402	0.40	0.10
Ni49–Te51/C	411	380	0.38	0.09
Ni39–Te61/C	415	384	0.37	0.10
Ni67–Te33/C	788	746	0.72	0.20
Ni60–Te40/C	779	749	0.70	0.19

---

Catalytic performance

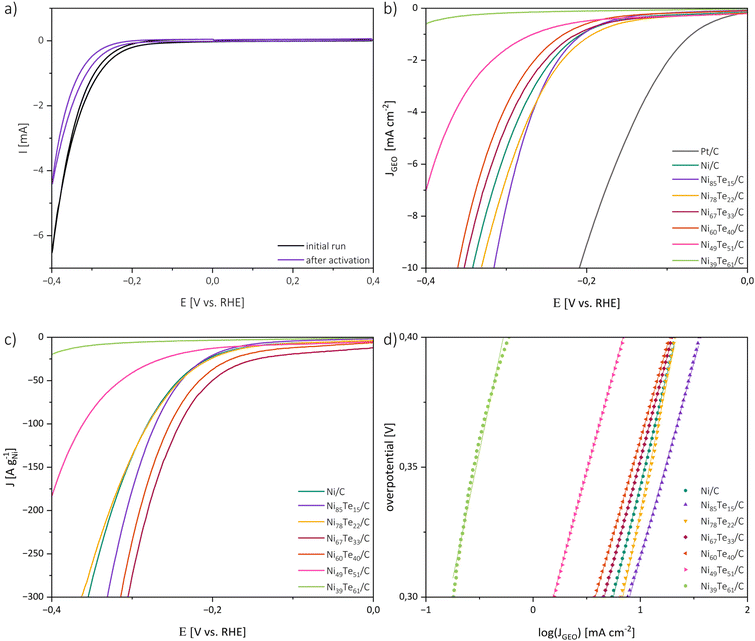
The catalytic activities of the catalysts in 1 M KOH were investigated by cyclic voltammetry (CV), linear sweep voltammetry (LSV) and electrochemical impedance spectroscopy (EIS). For the interpretation of the catalytic performance a few points must be considered. Firstly, the highly porous carbon black support does not noticeably participate in the HER but was employed to obtain a good dispersion of the active material at the surface. Therefore, it is expected that the catalytic performance is strongly dependent on the actual metal loading and the accessibility of the active sites of the respective intermetallic. In terms of practical design parameters for water splitting systems, normalizing the polarization curves to the geometric surface area, and benchmarking the activity at 10 mA cm⁻², which relates to at least 10% solar-to-hydrogen efficiency, is considered the conventional standard.^60,61 However, both the active metal loading and the specific surface area of the prepared electrode are strongly dependent on the (inter-)metallic content, particularly due to the relatively high atomic mass of tellurium. Hence, the mass activity, normalized to the amount of metal in the employed electrocatalyst, is expected to allow for a better understanding of the intrinsic catalytic performance and better comparability.

Fig. 6 shows the initial and final CV curve of Ni₈₅Te₁₅/C as a representative sample as well as the polarization curves normalized to the geometric surface area (S_geo), the mass activity and Tafel plots of the prepared catalysts. Besides the onset of the HER at potentials more cathodic than −0.1 V vs. RHE, the CV curves of the nickel-based materials did not show any significant peak in the potential range of interest, implying the absence of redox-reactions of the catalyst material. The CV curves of the other samples are presented in Fig. S3.†

Fig. 6 Cyclic voltammetry curves before and after activation cycling of Ni₈₅Te₁₅/C (a), polarization curves normalized to the geometric area (b), mass activity normalized to the nickel content (c) and Tafel plots (d).

The area normalized polarization curves reveal a positive effect of tellurium addition to a certain extent, but do not take the different nickel loadings of the electrode into account. Hence, the resulting performance is a counterpoise between the positive effect of tellurium addition and the lower absolute nickel concentration in the electrode. To overcome those limitations and get a deeper understanding on the effect tellurium intake has on the catalytic activity, the mass activity is a relevant parameter. Therefore, the polarization curves were additionally normalized to the nickel contents of the catalysts. Comparing the mass activities regarding sample composition reveals that the catalytic performance does not strictly follow the tellurium concentration but the formation of different intermetallic Ni–Te phases (see Table 3). The single-phase samples, Ni₃₉Te₆₁/C and Ni₄₉Te₅₁/C, have the highest tellurium concentrations and consist of the δ phase compound NiTe_2−x with low nickel occupation.⁵⁷ Their polarization curves do not reach the desired value of 10 mA cm⁻² in the potential range of interest, but as a trend, the catalytic activity increases with the nickel occupation. For the mixed-phase samples Ni₈₅Te₁₅/C and Ni₇₈Te₂₂/C a positive effect due to the presence of NiTe, a compound of the δ phase with high Ni occupation, was observed. The highest mass activities were achieved due to the presence of Ni₃Te₂ in the samples Ni₆₇Te₃₃/C and Ni₆₀Te₄₀/C. We conclude that the catalytic activity of the Ni–Te nanoparticles in 1 M KOH follows the particulate order of Ni₃Te₂ > NiTe > NiTe_2−x > NiTe₂. This trend appears to agree with literature when comparing different bulk studies, although a comprehensive comparison of all the intermetallic nickel tellurides was not published yet.

It is widely accepted that the HER takes place on the surface of the electrode by a multi-step electrochemical process including:⁶²

H₂O + e⁻ + M → M–H_ads + OH⁻ (Volmer) (1)

H₂O + e⁻ + M–H_ads → M + H₂ + OH⁻ (Heyrovsky) (2)

2M–H_ads → H₂ + 2M (Tafel) (3)

Here “M” refers to an active site of the electrocatalyst.

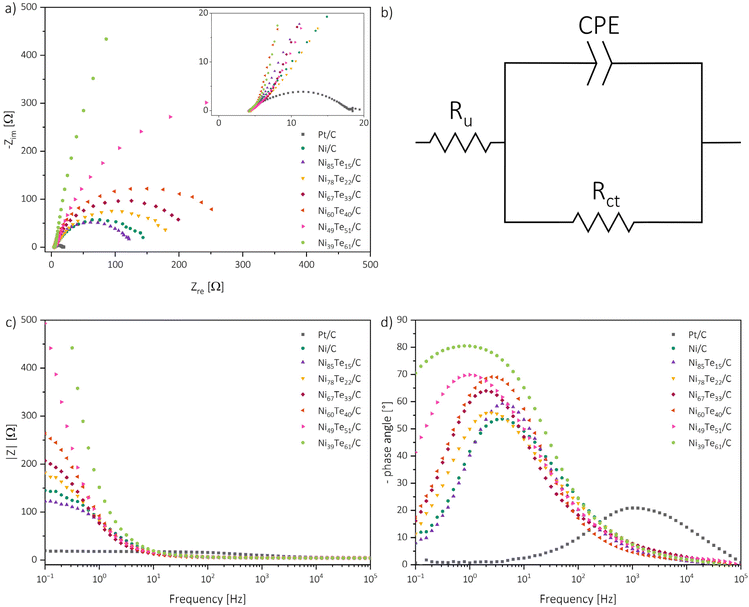
For the understanding of the reaction kinetics, Tafel plots were investigated in the high overpotential region of −0.4 to −0.3 V vs. RHE. The Tafel plots are presented in Fig. 6. The observed Tafel slopes >120 mV dec⁻¹ for all nickel-based catalysts indicate the Volmer step as rate determining step of the HER process. The reaction is therefore limited by the hydrogen adsorption and charge transfer rate of the catalyst. Those observations are supported by the results of electrochemical impedance spectroscopy (EIS) (Fig. 7).

Fig. 7 Nyquist plots (a), modified Randel's circuit (R_u = uncompensated solution resistance, CPE = constant phase element, R_ct = charge transfer resistance) (b), Bode absolute impedance plot (c) and Bode phase angle plot (d).

For each nickel-based catalyst only one time constant is observed in the Bode phase angle plot, with comparably high maximum phase angles between 54 to 81° at low peak frequencies in the regime of 1 to 4 Hz. Generally, higher maximum phase angles and lower peak frequencies are correlated to more sluggish reaction kinetics.⁶³ Interestingly, from that observation the Ni/C educt shows the fastest kinetics of the nickel based catalysts. For the intermetallic nickel tellurides again a higher nickel occupation in the δ phase occurs advantageous, NiTe furthermore shows improved HER kinetics compared to Ni₃Te₂. These observations highlight that the overall catalytic behaviour of the catalysts are not only determined by the reaction kinetics, but by the combination of many factors, like the surface admittance, charge transfer resistance of the interface, active surface area and the accessibility of the active sites.

The admittance acts as a measure of how facile an interface is for electron crossover. It was calculated as the reciprocal of the modulus of impedance by extrapolating the linear region in the Bode absolute impedance plot towards the lowest frequency of the experiments, where the charge transfer is solely controlled by the charge transfer resistance.⁶³

The charge transfer resistance, on the other hand, was obtained by fitting the Nyquist plots with a modified Randel's circuit.⁵¹ Bigger diameters of the semi-circles are related to increased charge transfer resistances. The presence of only one semi-circle per sample suggests that the reaction kinetics are dominated by one charge transfer step. Thus, EIS also indicates the charge transfer in the Volmer step to be the rate determining step of the process. As expected, the charge transfer resistance generally follows a contrary trend to the admittance and is increasing with the tellurium intake into Ni/C. Only the NiTe containing Ni₈₅Te₁₅/C sample has a lower charge transfer resistance and higher admittance than Ni/C.

The electrochemical active surface area (ECSA) was estimated from the double layer capacitance through assessment of CV measurements in the non-faradaic region (0.05–0.15 V vs. RHE) at different scan rates (Fig. S4; Table S3†).¹¹ The ECSA is dependent on the material loading as well as the crystal structure, and subsequently on the phase composition of the catalysts. Electrochemical data of the benchmarked catalysts are listed in Table 6. The comparison of the EIS and ECSA results helps to further understand the catalytic performance of the materials. While the admittance follows a contrary trend to the charge transfer resistance, the observed ECSA data does not align with the charge transfer parameter trend. Neither the charge transfer parameters, nor the ECSA data by itself are suited to explain the catalytic activities. The ECSA presents the total accessible surface for electrochemical reactions but does not provide information about the activity of the catalytically active sites. As mentioned above, the Volmer step, which was found to be the rate determining step, is not solely influenced by the charge transfer, but also the hydrogen adsorption activity of the catalytic sites. The charge transfer parameters of NiTe_2(−x) samples hint strong oppression, despite the high ECSA ultimately causing the weakest HER performance. The NiTe sample, on the other hand, showcased the most beneficial kinetics and charge transfer parameters, but the respective low ECSA, despite the minimal tellurium intake, hints meagre accessibility of the active sites. Thus, it is concluded that the formation of the intermetallic Ni₃Te₂ structure significantly improves the accessibility of the active nickel sites for HER in alkaline media. The increased accessibility in combination with good kinetics allow Ni₃Te₂ to outmatch the other nickel-based catalysts. The catalytic performance of the nickel tellurides follows the order mentioned before, Ni₃Te₂ > NiTe > NiTe_2−x > NiTe₂.

Table 6 Characteristic parameters observed from the catalytic activity investigations. (η₁₀ = overpotential vs. RHE at 10 mA cm⁻² normalized to the geometric surface area; η_os = onset-potential vs. RHE; b = Tafel slope; ω_pf = peak frequency; Y = admittance; Θ_max = maximum phase angle; R_ct = charge transfer resistance; ECSA = electrochemically active surface area.)

Sample	η 10 [mV]	η os [mV]	b [mV dec^−1]	ω pf [Hz]	Y [mS]	Θ max [°]	R ct [Ω]	ECSA [m^2 g^−1]
Ni/C	342	−155	171	4.0	5.7	53.6	145	46
Ni85–Te15/C	315	−158	150	4.0	6.3	59.2	116	31
Ni78–Te22/C	331	−149	172	2.5	5.0	56.0	186	67
Ni67–Te33/C	352	−145	157	2.0	4.3	64.0	204	60
Ni60–Te40/C	360	−146	144	2.5	3.4	69.1	283	29
Ni49–Te51/C	>400	−183	154	1.0	2.1	69.9	752	57
Ni39–Te61/C	>400	−229	141	0.8	0.9	80.5	5302	18

---

Stability and durability

The materials were investigated regarding their chemical as well as their catalytic stability and durability. Therefore, 12 h chronoamperometric measurements at a constant potential of −0.25 V vs. RHE were recorded. Before and after the chronoamperometric run, linear sweep polarization curves in cathodic scan direction were recorded and each 500 μl of the electrolyte solution were collected for TXRF spectroscopy investigation.

The absence of Ni, Te, and Fe traces in the TXRF spectra does not only hint on chemical stability of the materials, but also confirms that the “iron effect”,⁶⁴i.e. the change of activity through the doping with iron from electrolyte impurities, is excludable.

The chronoamperometry investigations depicted in Fig. 8 reveal two zones. An initial rapid decrease of the current density (t < 1 h) is followed by steady state conditions. The rapid catalyst aging effect is known for nickel catalysts,⁶⁵ possible causes include the charging of the electrical double layer, adsorption/desorption processes, surface restructuring and mass transport changes. The zig-zag form of Ni₈₅Te₁₅/C curve is caused by the formation of H₂ gas bubbles which are not removed efficiently from the electrode surface, this joins the observation of fast kinetics of the sample and highlights mass transport limitations in the particular case. An interesting trend is shown by the NiTe_2(−x) samples, as Ni₃₉Te₆₁/C and Ni₄₉Te₅₁/C become gradually activated over time. Possibly, surface reconstruction of the telluride species leads to lesser vacancy occupation which was found to be more active towards HER as described before.

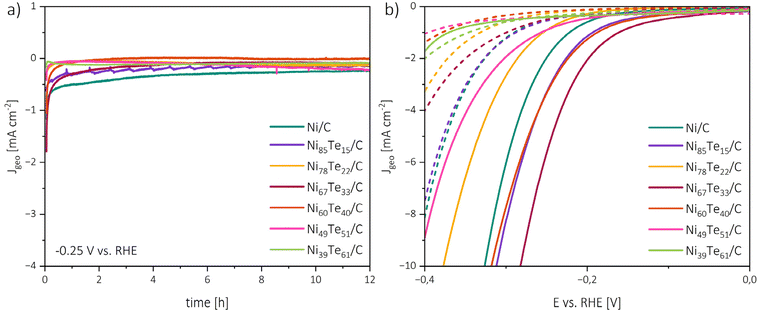Fig. 8 Chronoamperometry measurements at −0.25 V vs. RHE and 1600 rpm RDE rotation rate (a), polarization curves before chronoamperometry (solid lines) and after chronoamperometry (dashed lines) (b).

The initial rapid aging effect was also reflected in the comparison of the polarization curves before and after the 12 h chronoamperometric run. Besides Ni₃₉Te₆₁/C, for all catalysts a significant increase in the HER overpotentials was found. These observations lead to the conclusion that the catalysts are chemically stable and remain active during the reaction period in alkaline media, but the durability suffers from early deactivation processes.

Conclusion

In this report the facile vapour–solid synthesis approach was used to produce intermetallic nickel telluride nanoparticles with tellurium concentrations in the range of 0 at% to 61 at%. Characterization of the materials revealed remarkable compositional control. For the first time, carbon black supported nickel tellurides have been investigated regarding their hydrogen evolution reaction in alkaline media. The ability to benchmark and study whole intermetallic systems on their catalytic behaviour was demonstrated. Active site engineering by targeting different crystal structures and compositions was highlighted as a major advantage of the vapour–solid method. Identical synthesis parameters of the various nickel tellurides enabled a comprehensive comparison regarding their catalytic performance. In the future, this method could also be used for other intermetallic systems in order to efficiently develop and study a multitude of catalyst materials. Also, further investigation of different reaction temperatures, temperature gradients and dimensioning are of interest.

Author contributions

Daniel Garstenauer: writing – original draft, methodology, investigation, formal analysis, data curation, conceptualization, visualization. Patrick Guggenberger: writing – review & editing, methodology, investigation, formal analysis. Ondřej Zobač: writing – review & editing, methodology, investigation, formal analysis, resources. Franz Jirsa: writing – review & editing, formal analysis, resources. Klaus W. Richter: writing – review & editing, methodology, formal analysis, conceptualization, resources, project administration, validation, supervision.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

The authors wish to express their thanks to Dr Freddy Kleitz from the Department of Functional Materials and Catalysis, University of Vienna, for granting access to the physisorption and catalysis lab. Dr Ivo Kuběna, Institute of Physics of Materials, Czech Academy of Sciences, deserves our thanks for the advice on the interpretation of the microscopy results. The authors acknowledge the funding support of the University of Vienna, Austria. This research was further supported by Austria's Agency for Education and Internationalisation (OEAD) within the scientific & technological cooperation programme (CZ 06/2023).

References

1. IEA, World Energy Outlook 2023, International Energy Agency, Paris, 2023.
2. A. Zuttel, A. Remhof, A. Borgschulte and O. Friedrichs, Philos. Trans. R. Soc., A, 2010, 368, 3329–3342.
3. M. A. Rosen and S. Koohi-Fayegh, Energy, Ecol. Environ., 2016, 1, 10–29.
4. M. Genovese, A. Schlüter, E. Scionti, F. Piraino, O. Corigliano and P. Fragiacomo, Int. J. Hydrogen Energy, 2023, 48, 16545–16568.
5. Y. Gong, J. Yao, P. Wang, Z. Li, H. Zhou and C. Xu, Chin. J. Chem. Eng., 2022, 43, 282–296.
6. M. H. McCay and S. Shafiee, in Future Energy, 2020, pp. 475–493.  DOI:10.1016/b978-0-08-102886-5.00022-0.
7. J. D. Holladay, J. Hu, D. L. King and Y. Wang, Catal. Today, 2009, 139, 244–260.
8. T. Shinagawa and K. Takanabe, ChemSusChem, 2017, 10, 1318–1336.
9. L. Sun, Q. Luo, Z. Dai and F. Ma, Coord. Chem. Rev., 2021, 444, 214049.
10. M. Yu, E. Budiyanto and H. Tuysuz, Angew. Chem., Int. Ed., 2022, 61, e202103824.
11. C. C. McCrory, S. Jung, J. C. Peters and T. F. Jaramillo, J. Am. Chem. Soc., 2013, 135, 16977–16987.
12. H. Chen, X. Liang, Y. Liu, X. Ai, T. Asefa and X. Zou, Adv. Mater., 2020, 32, e2002435.
13. D. Yao, L. Gu, B. Zuo, S. Weng, S. Deng and W. Hao, Nanoscale, 2021, 13, 10624–10648.
14. B. You and Y. Sun, Acc. Chem. Res., 2018, 51, 1571–1580.
15. Y. Yang and M. Wei, J. Mater. Chem. A, 2020, 8, 2207–2221.
16. A. P. Tsai, S. Kameoka, K. Nozawa, M. Shimoda and Y. Ishii, Acc. Chem. Res., 2017, 50, 2879–2885.
17. M. Armbruster, Sci. Technol. Adv. Mater., 2020, 21, 303–322.
18. B. P. Williams, Z. Qi, W. Huang and C. K. Tsung, Nanoscale, 2020, 12, 18545–18562.
19. J. Li and S. Sun, Acc. Chem. Res., 2019, 52, 2015–2025.
20. W. J. Zeng, C. Wang, Q. Q. Yan, P. Yin, L. Tong and H. W. Liang, Nat. Commun., 2022, 13, 7654.
21. T. Y. Yoo, J. M. Yoo, A. K. Sinha, M. S. Bootharaju, E. Jung, H. S. Lee, B. H. Lee, J. Kim, W. H. Antink, Y. M. Kim, J. Lee, E. Lee, D. W. Lee, S. P. Cho, S. J. Yoo, Y. E. Sung and T. Hyeon, J. Am. Chem. Soc., 2020, 142, 14190–14200.
22. D. C. A. Ivarsson, U. Burkhardt, K. W. Richter, R. Kriegel, L. Rößner, M. Neumann and M. Armbrüster, J. Alloys Compd., 2018, 743, 155–162.
23. J. A. Rard, J. Solution Chem., 2019, 48, 271–282.
24. P. Wibner, Master's Thesis, University of Vienna, 2014.
25. P. Wibner, R. Kriegel, D. Garstenauer, O. Zobač, I. Kuběna, N. Rösch, T. Seyller, M. Armbrüster and K. W. Richter, J. Phys. Chem. C, 2024, 128, 6906–6916.
26. C. Hu, C. Lv, N. Zeng, A. Liu, Y. Liu, L. Hu, P. Li, Y. Yao, J. Cai and T. Tang, Energy Technol., 2022, 11, 2002435.
27. I. Amorim and L. Liu, Curr. Opin. Electrochem., 2022, 34, 101031.
28. S. Anantharaj, S. Kundu and S. Noda, J. Mater. Chem. A, 2020, 8, 4174–4192.
29. S. Anantharaj, K. Karthick and S. Kundu, Inorg. Chem., 2018, 57, 3082–3096.
30. K. S. Bhat and H. S. Nagaraja, Mater. Res. Innovations, 2019, 25, 29–52.
31. K. S. Bhat, H. C. Barshilia and H. S. Nagaraja, Int. J. Hydrogen Energy, 2017, 42, 24645–24655.
32. X. Chia, Z. Sofer, J. Luxa and M. Pumera, Chemistry, 2017, 23, 11719–11726.
33. U. De Silva, J. See, W. P. R. Liyanage, J. Masud, J. Wu, W. Yang, W.-T. Chen, D. Prendergast and M. Nath, Energy Fuels, 2021, 35, 4387–4403.
34. U. De Silva, J. Masud, N. Zhang, Y. Hong, W. P. R. Liyanage, M. Asle Zaeem and M. Nath, J. Mater. Chem. A, 2018, 6, 7608–7622.
35. U. De Silva, Doctor of Philosophy Doctoral Thesis, Missouri University of Science and Technology, 2021.
36. F. Mingli, L. Xue, W. Dandan, W. Yinling and L. Maoguo, Electrochim. Acta, 2019, 328, 135075.
37. R. Samal, C. Debbarma and C. S. Rout, Catal. Today, 2023, 424, 113880.
38. S. S. A. Shah, N. A. Khan, M. Imran, M. Rashid, M. K. Tufail, A. U. Rehman, G. Balkourani, M. Sohail, T. Najam and P. Tsiakaras, Membranes, 2023, 13, 113.
39. Z. Wang and L. Zhang, Electrochem. Commun., 2018, 88, 29–33.
40. Y. Xiang, K. Xiong, L. Yu, H. Zhang, J. Chen and M. Xia, J. Alloys Compd., 2022, 891, 161955.
41. W. Zheng, Y. Li, M. Liu and L. Y. S. Lee, Small, 2021, 17, e2007768.
42. H. Ren, Z.-H. Huang, Z. Yang, S. Tang, F. Kang and R. Lv, J. Energy Chem., 2017, 26, 1217–1222.
43. B. Predel, in Copyright 1998 Springer-Verlag Berlin Heidelberg, ed. O. Madelung, Springer-Verlag Berlin Heidelberg, 1998, vol. 51.
44. P. Juhás, J. N. Louwen, L. van Eijck, E. T. C. Vogt and S. J. L. Billinge, J. Appl. Crystallogr., 2018, 51, 1492–1497.
45. J. Barstard, F. Gronvold, E. Rost and E. Vestersjo, Acta Chem. Scand., 1966, 20, 2865–2879.
46. K. O. Klepp and K. L. Komarek, Monatsh. Chem., 1972, 103, 934–946.
47. J. S. Schubert, J. Popovic, G. M. Haselmann, S. P. Nandan, J. Wang, A. Giesriegl, A. S. Cherevan and D. Eder, J. Mater. Chem. A, 2019, 7, 18568–18579.
48. T. A. Centeno and F. Stoeckli, Carbon, 2010, 48, 2478–2486.
49. M. Kwiatkowski and E. Broniek, Materials, 2020, 13, 3929.
50. C. Schlumberger and M. Thommes, Adv. Mater. Interfaces, 2021, 8, 2002181.
51. S. Anantharaj and S. Noda, ChemElectroChem, 2020, 7, 2297–2308.
52. S. Anantharaj and S. Noda, Energy Adv., 2022, 1, 511–523.
53. C. Wei, R. R. Rao, J. Peng, B. Huang, I. E. L. Stephens, M. Risch, Z. J. Xu and Y. Shao-Horn, Adv. Mater., 2019, 31, e1806296.
54. L. Boulet-Roblin, D. Sheptyakov, P. Borel, C. Tessier, P. Novák and C. Villevieille, J. Mater. Chem. A, 2017, 5, 25574–25582.
55. W. Dang, X. Tang, W. Wang, Y. Yang, X. Li, L. Huang and Y. Zhang, Dalton Trans., 2020, 49, 10994–11004.
56. L. D. Gulay and I. D. Olekseyuk, J. Alloys Compd., 2004, 376, 131–138.
57. I. Jandl, H. Ipser and K. W. Richter, Calphad, 2015, 50, 174–181.
58. K. S. W. Sing, D. H. Everett, R. A. W. Haul, L. Mouscou, R. A. Pierotti, J. Rouquerol and T. Siemieniewska, Pure Appl. Chem., 1985, 57, 603–619.
59. M. Thommes, G. Q. Lu and X. S. Zhao, Physical Adsorption Characterization of Ordered and Amorphous Mesoporous Materials, Imperial College Press, Nanoporous Materials: Science and Engineering, 2004.
60. P. C. Vesborg, B. Seger and I. Chorkendorff, J. Phys. Chem. Lett., 2015, 6, 951–957.
61. J. D. Benck, T. R. Hellstern, J. Kibsgaard, P. Chakthranont and T. F. Jaramillo, ACS Catal., 2014, 4, 3957–3971.
62. F. Bao, E. Kemppainen, I. Dorbandt, R. Bors, F. Xi, R. Schlatmann, R. van de Krol and S. Calnan, ChemElectroChem, 2021, 8, 195–208.
63. S. Anantharaj, H. Sugime and S. Noda, J. Electroanal. Chem., 2021, 903, 511–523.
64. C. Zhang, Y. Bai, Y. Zhang, C. Li and S. Zhou, Results Phys., 2019, 14, 102522.
65. E. A. Franceschini, G. I. Lacconi and H. R. Corti, Electrochim. Acta, 2015, 159, 210–218.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr03397c

---