Open Access Article
Open Access ArticleHigh-efficiency prediction of water adsorption performance of porous adsorbents by lattice grand canonical Monte Carlo molecular simulation†
Zhilu
Liu
 a,
Wei
Li
a,
Wei
Li
 b and
Song
Li
b and
Song
Li
 *a
*a
aSchool of Energy and Power Engineering, Huazhong University of Science and Technology, Wuhan 430074, China
bEnergy & Electricity Research Center, Jinan University, Zhuhai, 519070, China. E-mail: songli@hust.edu.cn
First published on 18th November 2024
Abstract
Water adsorption has come under the spotlight for its tremendous potential in numerous environment- and energy-related applications. Given the vast adsorbent space, computational studies play a critically significant role in facilitating the discovery of potential candidates. However, large-scale computational deployment by conventional grand canonical Monte Carlo (GCMC) to identify optimal water adsorbents is challenging due to its extreme computation time and expense. In this work, a lattice GCMC method (LGCMC) with hierarchically constructed discretized interaction of host–guest and guest–guest driven by atomistic potentials was attempted to accurately and rapidly simulate the water adsorption performance of adsorbents using a coarse-grained Molinero water (mW) model. Nevertheless, given the monatomic nature of the mW model, leading to different phase behaviors in nanoscale confinement, a remarkable discrepancy in the primitive LGCMC-predicted isotherms, especially different step positions, compared with experiments was observed. Thus, a general correction strategy of water adsorption isotherm by tuning the saturation pressure was adopted. Taking metal–organic frameworks (MOFs) as examples, simulated water adsorption isotherms consistent with experimental results were obtained by the correction strategy using LGCMC. It is worth highlighting that the simulation of water adsorption in adsorbents by LGCMC can be accomplished within a few hours, which yields a significant acceleration of two to three orders of magnitude compared to conventional GCMC simulations. Therefore, the corrected LGCMC is a powerful tool to screen a huge number of adsorbents to facilitate the discovery of potential adsorbents for water adsorption-related applications, and this study provides microscopic insights into water adsorption mechanisms in porous adsorbents.
Introduction
Water is one of the necessities to guarantee the survival and development of mankind as well as the best green working medium in numerous environment- and energy-related applications owing to its abundance, non-toxicity and high enthalpy of evaporation.1 The adsorption phenomenon of water in porous adsorbents gave birth to a series of energy conservation and environmental protection thermal-driven applications, for example, adsorption water harvesting, desalination and purification for obtaining fresh water2–4 and adsorption heat pumps and chillers for producing heat or cold.5,6 The water adsorption performance of porous adsorbents including water stability, deliverable capacity and kinetics play a vital role in determining the application performance.7,8 In recent years, fast-growing novel adsorbents showing outstanding water adsorption performance such as metal–organic frameworks (MOFs)9 and covalent organic frameworks (COFs)10 have attracted much more attention than conventional adsorbents including zeolites, silica gels and porous carbons.11 The best candidates are various in different adsorption applications, for which the achievable performance of adsorbent/water working pairs not only is affected by operational conditions12 but also depends on diverse water adsorption characteristics such as hydrophilicity, water uptake, step position of adsorption isotherms and desorption hysteresis.1,13 Fundamentally, all these water adsorption characteristics can be acquired from water adsorption isotherms, which highlights the importance of acquiring water adsorption isotherms of various adsorbents for evaluating their potential in different applications.From the perspective of experiment, water adsorption isotherms of synthesized adsorbents can be tested using gas adsorption equipment and then be used as a primary basis for evaluating application performance. In recent years, novel adsorbents with excellent water adsorption performance have been continuously reported in various adsorption applications. For example, soc-MOF-1-Cr with a record-breaking water uptake of about 2 g g−1 at more than 70% relative humidity was regarded as a paragon in dehumidification applications.14 Subsequently, the reported MOF-801-Zr used for water harvesting from desert air, an Al-based MOF-303 delivering more than twice the amount of water (∼0.7 L kg−1 per day in the Mojave Desert) was developed, which benefits from its high deliverable water capacity (∼0.45 g g−1) at a low relative humidity of 10–30%.15,16 The MOFs ZJNU-30-Zr17 and CUK-1-Co18 and the COF TpPa-1 (ref. 19) with attractive water uptake and stepwise adsorption isotherms were recognized as potential candidates for adsorption chillers driven by a low-grade heat source. It is not difficult to obtain the water adsorption isotherms of several adsorbents, but it is impractical to synthesize and test thousands of adsorbents to identify the best performer for water adsorption. An effective machine learning (ML) model was successfully developed based on an experimental water adsorption isotherm database to predict water adsorption isotherms of various adsorbents. However, three experimental structural features (accessible surface area, available pore volume and pore diameter) as input descriptors were indispensable for executing the prediction procedure.20 It is still extremely challenging to comprehensively characterize all existing adsorbents, especially since around 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 synthesized records of MOFs were documented in the Cambridge Structural Database.21
000 synthesized records of MOFs were documented in the Cambridge Structural Database.21
From the perspective of computation, gas adsorption isotherms of a large number of adsorbents may be obtained from molecular simulation with the crystal structure of adsorbents, which can greatly reduce the experimental time and cost in the high-efficiency discovery of top performers, and have been successfully practiced in various applications such as carbon capture, methane storage and hydrogen storage.22–24 The conventional and most widely used approach for simulating water adsorption in porous materials is the grand canonical Monte Carlo (GCMC) simulation based on a grand canonical ensemble (μVT), which has been used to simulate water adsorption in porous carbon, zeolites and MOFs.25–27 For example, GCMC assists the exploration of the water adsorption mechanism in ZIF-8-Zn,28 the temperature effect on water adsorption and desorption processes in MIL-101-Cr,29,30 and the influence of structural defects on the water adsorption properties of Zr-based MOFs such as MOF-801-Zr (ref. 31) and UiO-66-Zr.32 In each GCMC cycle, the addition or deletion of water molecules is implemented and the total potential energy of the simulation system is calculated, and these processes are repeated till the system reaches equilibrium to output accurate water adsorption results. However, the hard truth is that an extremely long time is required to simulate water adsorption in adsorbents, up to tens of months of computational wall clock time on a single central processing unit (CPU) core to yield results, which is linked to the ultra-slow equilibrium convergence of the adsorbent/water system.28,31,33 Tracing it to its cause, except for time-consuming potential energy calculation in each cycle, the formation of water clusters during the water adsorption process due to the strong hydrogen-bonding networks causes a local free-energy minimum trap and thus leads to millions of cycles or a long time to reach equilibrium.28,34 Therefore, large-scale GCMC computational deployment to identify optimal water adsorbents can be very challenging due to its extremely high computation expense.
Several strategies have been proposed to accelerate the GCMC simulations. For example, the interactions between atoms of adsorbents and water molecules were precomputed on a grid to reduce the computation time of potential energy during the simulations. Paranthaman et al. executed water adsorption simulation in an Al(OH)(1,4-NDC) MOF and obtained consistent results with experimental water adsorption isotherms, in which 2 × 109 cycles were carried out.35 Another possible remedy is using a more efficient insertion and deletion strategy such as the continuous fractional component Monte Carlo (CFCMC),36 in which water molecules have a higher chance of being accepted by adding or removing molecules gradually rather than all of a sudden in regular GCMC. It has been shown to achieve convergence more rapidly than the regular GCMC in the case of water adsorption in MOF-806-Zr.34 Besides, other Monte Carlo methods were also attempted; the flat histogram method based on a canonical ensemble (NVT) was illustrated in simulating water adsorption of MOF-806-Zr,34 and Gibbs ensemble Monte Carlo (GEMC) based on Gibbs ensemble (NPT) was adopted to predict water adsorption isotherms of two Al-based MOF-303 and MOF-333.37 However, the consumed time of water adsorption simulation by the abovementioned approaches is not clearly stated; thus their feasibility in large-scale water adsorption simulation cannot be definitively assessed. To the best of our knowledge, a suitable approach to rapidly and accurately simulate water adsorption isotherms of porous adsorbents on a large scale is still in urgent development.
A simulation method based on a hierarchically constructed lattice model (i.e., the discretized free energy model replacing the continuous interaction of host–guest and guest–guest) driven by underlying atomistic potentials, named lattice GCMC method (LGCMC),38 has been developed to quickly estimate gas adsorption in porous materials and practiced in the prediction of CO2 adsorption isotherms in MOFs.38 In conjunction with appropriately coarse-grained guest–guest interactions, this method can offer agreement as compared to a fully atomistic GCMC simulation. Crucially, it yielded significant two to three orders of magnitude acceleration as compared to conventional GCMC simulations. In this work, LGCMC attempted to allow the use of a coarse-grained Molinero water (mW) model,39 which may provide the possibility of high-efficiency acquisition of water adsorption isotherms in porous adsorbents. Six typical MOFs were tested to verify the feasibility of LGCMC for efficiently simulating water adsorption isotherms. Eventually, we proved that simulated water adsorption isotherms of MOFs that are consistent with the experimental results can be obtained by LGCMC within several hours. Therefore, accurate and rapid simulation of water adsorption isotherms in porous materials was realized by LGCMC, which opens up the possibility for high-throughput screening of large-scale adsorbents in water adsorption-related applications.
Materials and methods
Lattice model description
Similar to conventional atomistic GCMC, the structure and geometry information of adsorbents were taken into account as input files of LGCMC. A given crystal unit cell is partitioned into an Na × Nb × Nc sub-lattice cell, where N is the number of divisions along the direct lattice vector to control the resolution of the grid. In the lattice model, the original continuous interaction potential energy of guest molecules within the unit cell is replaced with the corresponding discretized free energy at lattice cells, which is the key to determine the guest molecules adsorbed in a given adsorbent. It should be noted that the lattice approach in this work is used where adsorption space is divided into subspaces rather than into specific adsorption sites.40For the occupation configuration of guest molecules in a given crystal unit cell, the total free energy (Ftot) is approximated as eqn (1).
 | (1) |
Specifically, F(n) replacing the continuous interaction potential energy of guest molecules within adsorbents can be given by
F(n) = −kT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Qn Qn | (2) |
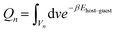 | (3) |
F int(n, m) is the discrete free energy of guest–guest interaction (Eguest–guest), which can be ignored in Henry's region (i.e., very low pressure and uptake), while the approximation of Fint(n, m) determines the accuracy of the total free energy (Ftot) when the uptake is high. The continuous interaction potentials of Eguest–guest must be discretized commensurate with the lattice grid to calculate the Fint(n, m). The straightforward discretization has been proven to work well.38
| Fint(n, m) = E(rnm) | (4) |
LGCMC simulations are executed on the constructed lattice model with a free energy grid including the host–guest and discretized guest–guest interactions. Three types of Monte Carlo moves including particle translations, insertions and deletions are performed in each cycle, in which a random guest is displaced on a random lattice according to the acceptance probability from the standard Metropolis scheme.38 The acceptance probabilities (p) are as follows.
| ptra = min(1, exp(−β(Ftrytot − Ftot))) | (5) |
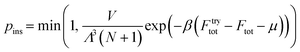 | (6) |
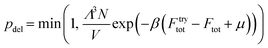 | (7) |
Model and force field parameters of adsorbent and guest molecules
In this work, experimental adsorption isotherms of MOFs in our updated experimental water adsorption isotherm database (EWAID)13,42 were selected as benchmarks to verify the accuracy of isotherms simulated by LGCMC. The crystal structures of such MOFs were collected from the Cambridge Crystallographic Data Centre (CCDC)43 and RASPA package.44 However, the existing difference between the structural properties of experimental samples and perfect crystals can be ascribed to the defects, unremoved solvents, or free ions in experimental samples.45 Besides, there are inevitable differences due to different evaluation methods, in which theoretical values are based on geometric methods (e.g., commonly using Zeo++) and experimental ones are usually based on analysis of nitrogen isotherms (e.g., BET method).46 The agreement between simulations and experiments is not expected for those adsorbents with inconsistent structural properties.45 Thus, to exclude the influence of differences in structural properties on the prediction results to the greatest extent, six MOFs (in Table 1) with consistent theoretical and experimental structural properties including accessible surface area (Sa), available pore volume (Va) and pore diameter (Dp) were eventually adopted. The process for selecting MOFs is shown in Fig. S1,† and their literature source and structural properties are provided in Table S1.†| No. | Adsorbents | Mea. Sa (m2 g−1) | Mea. Va (cm3 g−1) | Mea. Dp (Å) | Com. Sa (m2 g−1) | Com. Va (cm3 g−1) | Com. LCD (Å) |
|---|---|---|---|---|---|---|---|
| 1 | Al(OH)-(1,4-NDC)47 | 546 | 0.22 | 7.70 | 614 | 0.19 | 7.48 |
| 2 | DUT-67-Zr (ref. 48) | 1560 | 0.60 | 16.60 | 1808 | 0.54 | 17.05 |
| 3 | MIL-100-Fe (ref. 49) | 1549 | 0.82 | 29.00 | 1931 | 0.88 | 26.60 |
| 4 | MIL-101-Cr (ref. 50) | 3124 | 1.58 | 34.00 | 3026 | 1.61 | 33.66 |
| 5 | MOF-74-Mg (ref. 50) | 1400 | 0.65 | 11.00 | 1708 | 0.67 | 11.87 |
| 6 | MUF-77-Zn-methyl (ref. 51) | 3600 | 1.85 | 21.10 | 4437 | 1.68 | 21.78 |
For the host–guest interaction (Ehost–guest here is EMOF-water), selected MOFs and the Tip4p water model were considered in this work. Their interaction includes both van der Waals (12-6 Lennard-Jones) and coulombic potential as shown in eqn (8).
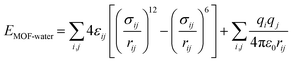 | (8) |
The discretized guest–guest interaction (Eguest–guest) in specific adsorbents was calculated. In this work, the guest is coarse-grained mW, which represents each water molecule by a single particle with tetrahedral interactions. The mW model potential39,57 uses the short-range interaction form of the Stillinger–Weber potential, consisting of a sum of two-body attraction terms that favor high coordination, and three-body repulsion terms that reinforce tetrahedral hydrogen-bonded configurations (eqn (9)).
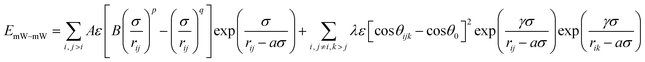 | (9) |
LGCMC simulations
In the LGCMC simulation, the adsorption condition was reflected by the chemical potential (μ), and it is used to evaluate the acceptance probabilities of particle translation moves. The chemical potential depends on the adsorption conditions (temperature and pressure) and the properties of the guest molecule. | (10) |
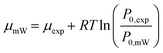 | (11) |
In this work, a total of 2 × 107 cycles including 1 × 107 cycles for equilibration and 1 × 107 cycles for production were implemented. The manual and original simulation code of LGCMC can be found on the websites of Schmidt's group.61 Output results including water uptake, the heat of adsorption and water distribution in adsorbents can be obtained from LGCMC. In our pre-test, the LGCMC simulations are extremely rapid and typically finish within a few minutes using a single CPU core, which benefits from the exclusive use of the pre-tabulated discretized free energy model. As such, the majority of the computational cost of simulation is contributed by the generation of a free energy model.
Results and discussion
Grid size optimization
For a given adsorbent, the grid size determining the resolution of the lattice cell is one of the most important factors affecting the computational time of the free energy model. In the construction of the lattice model, the periodic boundary conditions were used, and the unit cell size of MOFs was set to larger than twice the cutoff (i.e., larger than 15 Å). For specific MOFs, the number of gridded sub-cells depends on the size of their unit cell (Table S5† shows the size of the crystal unit cell for six MOFs used in this work) and grid size. Owing to the trade-off between the high precision and the long computational time of the free energy model using a small grid size, grid size optimization was performed first. The representative MOFs, MOF-74-Mg, DUT-67-Zr and MIL-101-Cr with small-size (<30 Å), medium-size (30–50 Å) and large-size (>50 Å) unit cells, respectively, were chosen for LGCMC under varying grid sizes (0.5 Å, 1 Å and 2 Å). It is indicated that the equilibrium water uptakes obtained using smaller grid sizes (0.5 Å and 1 Å) are slightly higher than that using a large grid size of 2 Å (Fig. 1), which may be due to the high-precision free energy model increasing the insertion sites of the water molecule. The water uptake values obtained using grid sizes of 0.5 Å and 1 Å are almost exactly the same, but there is a huge difference in computational cost. Taking MIL-101-Cr with a large-size unit cell as an example, a computation time of about 24 h is required to produce the free energy grid with a grid size of 1 Å, while around 200 h is needed for a grid size of 0.5 Å. Therefore, taking both the computational precision and time into account, a grid size of 1 Å was adopted for the computation of free energy. The free energy maps of most adsorbents can be obtained within a few hours in our tests.Water adsorption isotherms by LGCMC
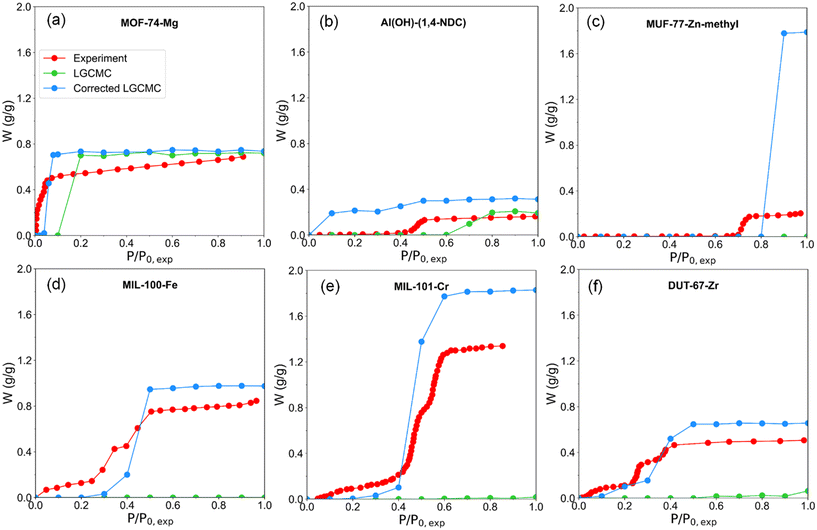
The water adsorption isotherms of six MOFs were simulated using LGCMC at 298 K and compared with reported experimental results (Fig. 2). Two important indexes including water uptake (W) and step position of isotherms (α) were focused on. In this work, α was defined as the relative pressure when half of the saturation water uptake was reached. In experiments, MOF-74-Mg shows a type I (i.e., inverted L shape) water adsorption isotherm; the MOFs Al(OH)-(1,4-NDC) and MUF-77-Zn-methyl exhibit type V (i.e., S shape) isotherms, and the rest of the MOFs MIL-100-Fe, MIL-101-Cr and DUT-67-Zr with hierarchical pores show type VI isotherms with multiple adsorption steps. LGCMC simulations successfully predicted similar isotherms for MOF-74-Mg and Al(OH)-(1,4-NDC) with slightly higher saturation water uptake and larger step position of the isotherm (i.e., αLGCMC > αexp). However, almost no water uptake throughout the pressure range (P/P0,exp = 0–1) was observed in the predicted isotherms of the other four MOFs. A rapid increase in water uptake in the LGCMC isotherm was observed at P/P0,exp >1 (Fig. 2 and S3†). For example, a rapid increase in water uptake was observed at P/P0,exp = 2–3 (i.e., αLGCMC) for MIL-100-Fe and MIL-101-Cr, P/P0,exp = 3–4 for DUT-67-Zr and P/P0,exp = 6–7 for MUF-77-Zn-methyl; all of them are larger than αexp in experimental water adsorption isotherms. It also indicates that the saturation vapor pressure of mW in LGCMC simulation isotherms is larger in the theoretical than the experimental measured result. | ||
| Fig. 2 Experimental water adsorption isotherms collected from the literature (sources provided in Table 1) and simulated water adsorption isotherms of MOFs by LGCMC. The inset figures show the LGCMC simulation at P/P0,exp >1. (a) MOF-74-Mg with a type I isotherm (i.e., inverted L shape), (b) Al(OH)-(1,4-NDC) and (c) MUF-77-Zn-methyl with type V (i.e., S shape) isotherms, (d) MIL-100-Fe, (e) MIL-101-Cr and (f) DUT-67-Zr with multiple-step isotherms. αLGCMC is the step position of LGCMC isotherms. | ||
In order to eliminate the discrepancy of the saturation vapor pressure between mW and experimental water in the bulk phase, P0,exp was used instead of P0,mW (eqn (11)). However, the phase behaviors of adsorbed water molecules confined in nanoporous materials are still significantly different from that of bulk water.62 The monatomic mW model with a loss of rotational entropy makes it hard to accurately reproduce the phase behaviors of adsorbed water under nanopore confinement effects, which leads to the difference between the saturation pressure of mW and that of experimental water in nanoporous adsorbents. Therefore, the difference in saturation pressures between mW and experimental water due to the nanoconfinement effects needs to be further corrected.
Isotherm correction
The quantification of the differences in saturation pressures of mW and experimental water is crucial for accurate correction, but the saturation pressure of mW in nanopores is difficult to predict, which complicates this process. In nanopores, the pressure of water in the nanopore beginning or undergoing phase transition can be described by the condensation pressure (Pc, vapor to liquid phase during adsorption). Assuming that the nanopore confinement effects on the phase behavior of mW and experimental water are equivalent under varying pressures, then the difference in condensation pressures between mW and experimental water can also reflect differences in saturation pressures. In previous studies on water adsorption, the condensation pressure represents the water uptake that begins to rapidly increase in water adsorption isotherms;58,63,64 thus, the condensation pressure can be estimated according to the adsorption isotherms.As for the mW in adsorbents, the condensation pressure (Pc,mW) can be identified based on the LGCMC simulated isotherms. Besides, the condensation relative pressure (Pc,mW/P0,exp) coincides with the step position of isotherms (αLGCMC) in this work. As for the experimental water in adsorbents, there is a problem in obtaining the condensation pressure of experimental water in adsorbents. First of all, direct experimental measurement of the phase transition pressure of water in nanoconfinement is very difficult. Secondly, the determination of condensation pressure based on the experimental water adsorption isotherm of the adsorbent is contrary to the original intention of simulations. Fortunately, the water condensation phenomena in nanoconfinement can be described by the century-old Kelvin equation (eqn (12)). The condensation pressure of confined water (Pc,Kelvin) in nanopores can be estimated using the Kelvin equation. In particular, the Kelvin equation has been proven applicable to atomic-scale confinement with a pore size of around 4 Å,65 including MOFs.63,64
The computation details are described as follows.
 | (12) |
 | ||
| Fig. 3 The relationship between the contact angle (θ) of water in nanopores and the condensation relative pressure (Pc,mW/P0,exp) of water adsorption isotherms. The contact angles of mW were adapted based on a series of cylindrical nanopores with different hydrophilicity, and the condensation relative pressures were extracted from their predicted water adsorption isotherms by GCMD simulations from Factorovich et al.'s work.58 | ||
Compared with the condensation pressure (Pc,mW) from isotherms by LGCMC, the difference between the condensation pressures from the Kelvin equation (Pc,Kelvin) and Pc,mW can be converted to the difference in chemical potential by Δμ (schematic diagram in Fig. 4; Table S6† provides the Δμ of six MOFs in this work). Assuming that the chemical potential difference (Δμ) of each adsorbent is identical throughout the pressure range, thus, the corrected chemical potential (μcor) at varying pressures for each adsorbent in LGCMC simulations was obtained by eqn (13).
 | (13) |
Besides, water adsorption isotherms obtained by LGCMC were also compared with the results from conventional GCMC based on the atomistic water model by other researchers (Fig. 6). The saturation water uptake obtained by atomistic GCMC is generally consistent with LGCMC, which indicates that it is able to provide a quantitatively accurate prediction while using the same perfect crystal structure in simulation. The step positions of isotherms from atomistic GCMC is inevitably slightly overestimated (e.g., MOF-74-Mg (ref. 26)) or underestimated (e.g., Al(OH)-(1,4-NDC)35 and MIL-101-Cr (ref. 30)) compared with experiments. It should be noted that the atomistic GCMC isotherm of Al(OH)-(1,4-NDC) showing type V in Fig. 6b was obtained by scaling all partial charges of framework atoms down to about 30% for better reproducing the experimental adsorption isotherm, which in fact weakens the interactions between water and adsorbents.35 Without scaling the atomic charges of Al(OH)-(1,4-NDC) by LCGMC in previously reported work and this work, the water adsorption takes place at low pressure with a small step position owing to the strong interaction with water molecules.35 When using the same force field parameters of Al(OH)-(1,4-NDC) as in the literature,35 LGCMC obtains a consistent adsorption isotherm with atomistic GCMC and experiment (Fig. 6b and S4†). In contrast with GCMC, it has to be emphasized that the computation cost of LGCMC is within a few hours for most MOFs, which is the most attractive aspect of using LGCMC. Overall, the correction strategy of LGCMC simulation is effective in achieving consistent isotherms with the experiment and atomistic GCMC simulation.
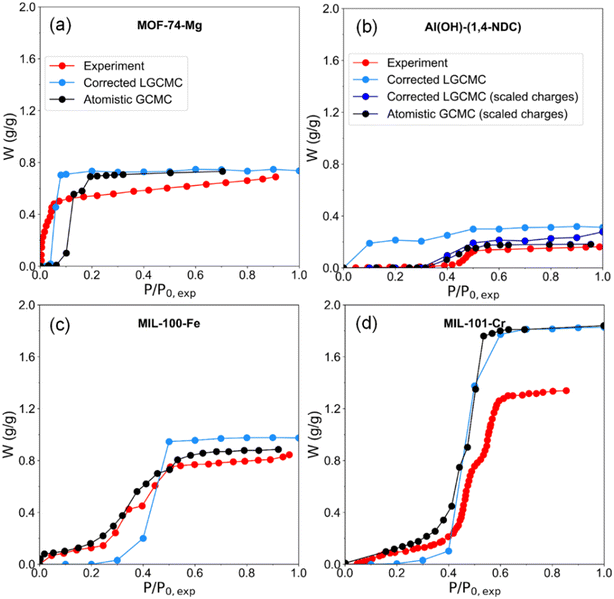 | ||
| Fig. 6 Experimental and GCMC simulated water adsorption isotherms of MOFs, in which the isotherm by GCMC simulation is extracted from other studies. (a) MOF-74-Mg,26 (b) Al(OH)-(1,4-NDC),35 (c) MIL-100-Fe,67 and (d) MIL-101-Cr.30 It should be noted that the isotherms of “corrected LGCMC (scaled charges)” and “atomistic GCMC (scaled charges)”35 of Al(OH)-(1,4-NDC) were obtained using the same force field. | ||
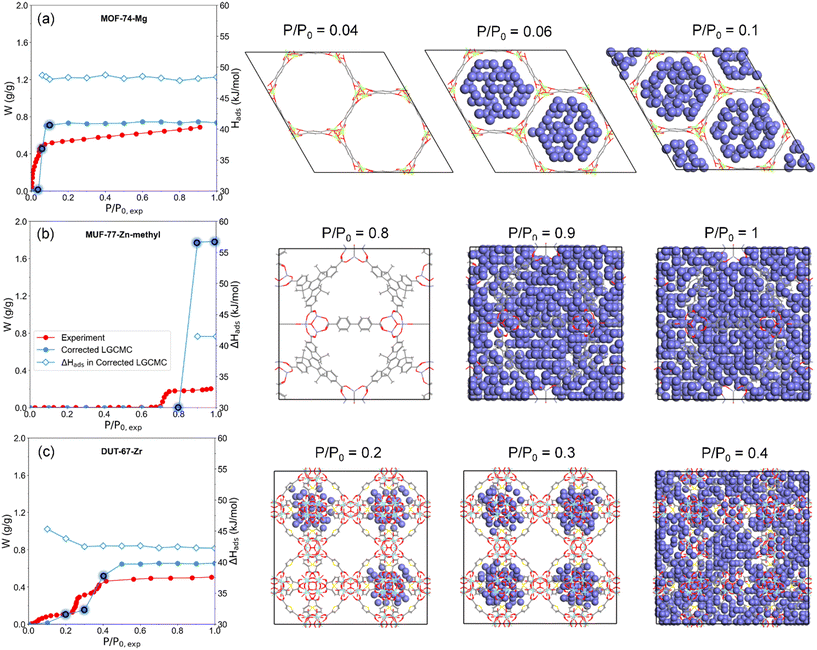
Water adsorption behaviors and heat of adsorption
Based on the water adsorption isotherms obtained by LGCMC, the performance of applications focusing on the water delivery capacity such as water harvesting and desalination can be easily and directly evaluated according to the water uptake of adsorbents under operation conditions. Not only the water uptake but also the corresponding heat of adsorption (Hads) can be obtained from LGCMC simulations (examples in Fig. 7). Thus, the performance of water adsorption-related applications with an energy conversion process, such as adsorption chillers or heat pumps, including cooling/heat capacity and energy conversion efficiency can be predicted.Besides, users can explore the water adsorption mechanism by LGCMC based on the trajectory of mW molecules in adsorbents. Taking three MOFs with different isotherm types as examples (Fig. 7), the snapshots of water molecule distribution during the adsorption process in MOFs were displayed. As for MOF-74-Mg with a type I isotherm and MUF-77-Zn-methyl with a type V isotherm, water molecules fill their accessible pores instantaneously. The lower pressure of MOF-74-Mg than MUF-77-Zn-methyl resulting in different shapes of adsorption isotherms is mainly attributed to its stronger hydrophilicity or stronger interaction between MOFs and water. In DUT-67-Zr with two pore sizes, water molecules preferentially adsorb in the small pores in the form of water clusters at low pressure, and then fill large pores at high pressure. Thus, not only the isotherm with the characteristics of two adsorption steps is reproduced but also the corresponding water adsorption behaviors can be explored.
Conclusions
In this work, we demonstrated lattice GCMC (LGCMC) simulation using a coarse-grained mW model to accurately and rapidly predict water adsorption isotherms of porous adsorbents within a few hours. Water adsorption isotherms of adsorbents obtained by primitive LGCMC under the chemical potential for the mW model (μmW) cannot accurately predict the step position of isotherms compared to experimental ones. Thus, we proposed an isotherm correction strategy to improve the consistency by correcting the difference in saturation pressure between mW from LGCMC and experimental water in nanoconfinement, in which the condensation pressure of confined water in each adsorbent was obtained from the Kelvin equation. The difference in saturation pressure was then converted to the chemical potential (μcor) for the corrected LGCMC simulation. Based on the correction strategy, the water adsorption isotherms obtained by LGCMC exhibit improved consistency with experimental results. It should be noted that the complicated channel and surface heterogeneity of MOFs including various pore sizes, shapes and connectivity add up to the difficulty in accurate prediction of their water adsorption performance. The simplification of the physical properties inside the MOFs during estimation of the contact angle and Kelvin condensation pressure in our correction strategy may cause over- or underestimation of the step positions of water isotherms. For MOFs with open metal sites such as MOF-74-Mg, MIL-100-Fe and MIL-101-Cr, using a more accurate force field from first principles methods may further improve the prediction accuracy. However, there is no doubt that it is an effective strategy for the prediction of water adsorption isotherms of various adsorbents.Besides, not only the water uptake but also the corresponding heat of adsorption and the distribution of water molecules in adsorbents can be obtained from LGCMC, which permits the performance evaluation of water adsorption-driven systems, including water delivery capacity and energy conversion efficiency, and enables the in-depth understanding of the microscopic mechanism of water adsorption behaviors in adsorbents. It has to be emphasized that the total computation time of LGCMC can be accomplished within a few hours for most adsorbents, which yields a significant acceleration of two to three orders of magnitude compared to conventional atomistic GCMC simulations. The LGCMC approach reported in this work opens up the possibility for high-throughput computational screening of an enormous number of adsorbents as well as greatly speeds up the discovery of potential adsorbent candidates in water adsorption-related applications.
Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (Grant No. 52306012). We are grateful to Randall Q. Snurr (Northwestern University, USA) and Jesse G. McDaniel (Georgia Institute of Technology, USA) for their valuable feedback and discussions.References
- M. Xu, Z. Liu, X. Huai, L. Lou and J. Guo, Screening of metal-organic frameworks for water adsorption heat transformation using structure-property relationships, RSC Adv., 2020, 10(57), 34621–34631 RSC.
- N. Singh, G. Nagpal and S. Agrawal, Water purification by using adsorbents: a review, Environ. Technol. Innovation, 2018, 11, 187–240 CrossRef.
- H. Lu, W. Shi, Y. Guo, W. Guan, C. Lei and G. Yu, Materials engineering for atmospheric water harvesting: progress and perspectives, Adv. Mater., 2022, 34(12), 2110079 CrossRef CAS PubMed.
- B. Qiu, P. Gorgojo and X. Fan, Adsorption desalination: Advances in porous adsorbents, Chin. J. Chem. Eng., 2022, 42, 151–169 CrossRef CAS.
- M. F. de Lange, K. J. Verouden, T. J. Vlugt, J. Gascon and F. Kapteijn, Adsorption-Driven Heat Pumps: The Potential of Metal-Organic Frameworks, Chem. Rev., 2015, 115(22), 12205–12250 CrossRef CAS PubMed.
- P. R. Chauhan, S. C. Kaushik and S. K. Tyagi, Current status and technological advancements in adsorption refrigeration systems: A review, Renewable Sustainable Energy Rev., 2022, 154, 111808 CrossRef.
- R. Al-Dadah, S. Mahmoud, E. Elsayed, P. Youssef and F. Al-Mousawi, Metal-organic framework materials for adsorption heat pumps, Energy, 2020, 190, 116356 CrossRef CAS.
- X. Zhou, H. Lu, F. Zhao and G. Yu, Atmospheric water harvesting: a review of material and structural designs, ACS Mater. Lett., 2020, 2(7), 671–684 CrossRef CAS.
- X. Liu, X. Wang and F. Kapteijn, Water and Metal-Organic Frameworks: From Interaction toward Utilization, Chem. Rev., 2020, 120(16), 8303–8377 CrossRef CAS PubMed.
- S.-Y. Ding and W. Wang, Covalent organic frameworks (COFs): from design to applications, Chem. Soc. Rev., 2013, 42(2), 548–568 RSC.
- L. W. Wang, R. Z. Wang and R. G. Oliveira, A review on adsorption working pairs for refrigeration, Renewable Sustainable Energy Rev., 2009, 13(3), 518–534 CrossRef CAS.
- Z. Liu, W. Li, S. Cai, Z. Tu, X. Luo and S. Li, Screening versatile water/adsorbent working pairs for wide operating conditions of adsorption heat pumps, Sustainable Energy Fuels, 2022, 6(2), 309–319 RSC.
- Z. Liu, W. Li, P. Z. Moghadam and S. Li, Screening adsorbent–water adsorption heat pumps based on an experimental water adsorption isotherm database, Sustainable Energy Fuels, 2021, 5(4), 1075–1084 RSC.
- S. M. Towsif Abtab, D. Alezi, P. M. Bhatt, A. Shkurenko, Y. Belmabkhout, H. Aggarwal, Ł. J. Weseliński, N. Alsadun, U. Samin, M. N. Hedhili and M. Eddaoudi, Reticular Chemistry in Action: A Hydrolytically Stable MOF Capturing Twice Its Weight in Adsorbed Water, Chem, 2018, 4(1), 94–105 CAS.
- F. Fathieh, M. J. Kalmutzki, E. A. Kapustin, P. J. Waller, J. Yang and O. M. Yaghi, Practical water production from desert air, Sci. Adv., 2018, 4(6), eaat3198 CrossRef.
- N. Hanikel, M. S. Prévot, F. Fathieh, E. A. Kapustin, H. Lyu, H. Wang, N. J. Diercks, T. G. Glover and O. M. Yaghi, Rapid Cycling and Exceptional Yield in a Metal-Organic Framework Water Harvester, ACS Cent. Sci., 2019, 5(10), 1699–1706 CrossRef CAS PubMed.
- A. Luna-Triguero, A. Sławek, H. P. Huinink, T. J. H. Vlugt, A. Poursaeidesfahani, J. M. Vicent-Luna and S. Calero, Enhancing the water capacity in Zr-Based metal-organic framework for heat pump and atmospheric water generator applications, ACS Appl. Nano Mater., 2019, 2(5), 3050–3059 CrossRef CAS.
- J. S. Lee, J. W. Yoon, P. G. M. Mileo, K. H. Cho, J. Park, K. Kim, H. Kim, M. F. de Lange, F. Kapteijn, G. Maurin, S. M. Humphrey and J. S. Chang, The porous metal-organic framework CUK-1 for adsorption heat allocation toward green applications of natural refrigerant water, ACS Appl. Mater. Interfaces, 2019, 11(29), 25778–25789 CrossRef CAS.
- J. Perez-Carvajal, G. Boix, I. Imaz and D. Maspoch, The Imine-based COF TpPa-1 as an efficient cooling adsorbent that can be regenerated by heat or light, Adv. Energy Mater., 2019, 9(39), 1901535 CrossRef CAS.
- Z. Liu, D. Shen, S. Cai, Z. Tu and S. Li, Machine Learning-Assisted Prediction of Water Adsorption Isotherms and Cooling Performance, J. Mater. Chem. A, 2023, 11(36), 19455–19464 RSC.
- H. Daglar and S. Keskin, Recent advances, opportunities, and challenges in high-throughput computational screening of MOFs for gas separations, Coord. Chem. Rev., 2020, 422, 213470 CrossRef CAS.
- D. A. Gómez-Gualdrón, Y. J. Colón, X. Zhang, T. C. Wang, Y.-S. Chen, J. T. Hupp, T. Yildirim, O. K. Farha, J. Zhang and R. Q. Snurr, Evaluating topologically diverse metal–organic frameworks for cryo-adsorbed hydrogen storage, Energy Environ. Sci., 2016, 9(10), 3279–3289 RSC.
- S. Li, Y. G. Chung and R. Q. Snurr, High-Throughput Screening of Metal-Organic Frameworks for CO2 Capture in the Presence of Water, Langmuir, 2016, 32(40), 10368–10376 CrossRef CAS PubMed.
- M. Tong, Y. S. Lan, Q. Y. Yang and C. L. Zhong, High-throughput computational screening and design of nanoporous materials for methane storage and carbon dioxide capture, Green Energy Environ., 2018, 3(2), 107–119 CrossRef.
- V. T. Nguyen, P. T. M. Nguyen, L. X. Dang, D. Mei, C. D. Wick and D. D. Do, A comparative study of the adsorption of water and methanol in zeolite BEA: a molecular simulation study, Mol. Simul., 2014, 40(14), 1113–1124 CrossRef CAS.
- X. Peng, L.-C. Lin, W. Sun and B. Smit, Water adsorption in metal-organic frameworks with open-metal sites, AIChE J., 2015, 61(2), 677–687 CrossRef CAS.
- L. Sarkisov, A. Centineo and S. Brandani, Molecular simulation and experiments of water adsorption in a high surface area activated carbon: Hysteresis, scanning curves and spatial organization of water clusters, Carbon, 2017, 118, 127–138 CrossRef CAS.
- H. Zhang and R. Q. Snurr, Computational study of water adsorption in the hydrophobic metal-organic framework ZIF-8: Adsorption mechanism and acceleration of the simulations, J. Phys. Chem. C, 2017, 121(43), 24000–24010 CrossRef CAS.
- S. Fei, A. Alizadeh, W.-L. Hsu, J.-J. Delaunay and H. Daiguji, Analysis of the Water Adsorption Mechanism in Metal–Organic Framework MIL-101(Cr) by Molecular Simulations, J. Phys. Chem. C, 2021, 125(48), 26755–26769 CrossRef CAS.
- S. Fei, J. Gao, R. Matsuda, A. Endo, W.-L. Hsu, J.-J. Delaunay and H. Daiguji, Temperature effect on water adsorption and desorption processes in the mesoporous metal-organic framework MIL-101(Cr), J. Phys. Chem. C, 2022, 126(36), 15538–15546 CrossRef CAS.
- J. Choi, L.-C. Lin and J. C. Grossman, Role of structural defects in the water adsorption properties of MOF-801, J. Phys. Chem. C, 2018, 122(10), 5545–5552 CrossRef CAS.
- P. Ghosh, Y. J. Colon and R. Q. Snurr, Water adsorption in UiO-66: the importance of defects, Chem. Commun., 2014, 50(77), 11329–11331 RSC.
- A. Datar, M. Witman and L. C. Lin, Monte Carlo simulations for water adsorption in porous materials: Best practices and new insights, AIChE J., 2021, 67(12), 1–13 CrossRef.
- A. Datar, M. Witman and L.-C. Lin, Improving Computational Assessment of Porous Materials for Water Adsorption Applications via Flat Histogram Methods, J. Phys. Chem. C, 2021, 125(7), 4253–4266 CrossRef CAS.
- S. Paranthaman, F. X. Coudert and A. H. Fuchs, Water adsorption in hydrophobic MOF channels, Phys. Chem. Chem. Phys., 2010, 12(28), 8123–8129 RSC.
- W. Shi and E. J. Maginn, Continuous fractional component Monte Carlo: An adaptive biasing method for open system atomistic simulations, J. Chem. Theory Comput., 2007, 3(4), 1451–1463 CrossRef CAS PubMed.
- S. Chheda, W. Jeong, N. Hanikel, L. Gagliardi and J. I. Siepmann, Monte Carlo Simulations of Water Adsorption in Aluminum Oxide Rod-Based Metal–Organic Frameworks, J. Phys. Chem. C, 2023, 127(16), 7837–7851 CrossRef CAS.
- K. Yu, J. G. McDaniel and J. R. Schmidt, An efficient multi-scale lattice model approach to screening nano-porous adsorbents, J. Chem. Phys., 2012, 137(24), 244102 CrossRef.
- V. Molinero and E. B. Moore, Water modeled as an intermediate element between carbon and silicon, J. Phys. Chem. B, 2009, 113(13), 4008–4016 CrossRef CAS PubMed.
- A. Kundu, K. Sillar and J. Sauer, Ab Initio Prediction of Adsorption Isotherms for Gas Mixtures by Grand Canonical Monte Carlo Simulations on a Lattice of Sites, J. Phys. Chem. Lett., 2017, 8(12), 2713–2718 CrossRef CAS PubMed.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, A smooth particle mesh Ewald method, J. Chem. Phys., 1995, 103(19), 8577–8593 CrossRef CAS.
- Z. Liu, W. Li, S. Cai, Z. Tu, X. Luo and S. Li, Large-scale cascade cooling performance evaluation of adsorbent/water working pairs by integrated mathematical modelling and machine learning, J. Mater. Chem. A, 2022, 10(17), 9604–9611 RSC.
- Cambridge Crystallographic Data Centre (CCDC), https://www.ccdc.cam.ac.uk/, (accessed 1 Oct., 2022).
- D. Dubbeldam, S. Calero, D. E. Ellis and R. Q. Snurr, RASPA: molecular simulation software for adsorption and diffusion in flexible nanoporous materials, Mol. Simul., 2015, 42(2), 81–101 CrossRef.
- D. Ongari, L. Talirz, K. M. Jablonka, D. W. Siderius and B. Smit, Data-Driven Matching of Experimental Crystal Structures and Gas Adsorption Isotherms of Metal–Organic Frameworks, J. Chem. Eng. Data, 2022, 67(7), 1743–1756 CrossRef CAS.
- J. W. M. Osterrieth, J. Rampersad, D. Madden, N. Rampal, L. Skoric, B. Connolly, M. D. Allendorf, V. Stavila, J. L. Snider, R. Ameloot, J. Marreiros, C. Ania, D. Azevedo, E. Vilarrasa-Garcia, B. F. Santos, X. H. Bu, Z. Chang, H. Bunzen, N. R. Champness, S. L. Griffin, B. Chen, R. B. Lin, B. Coasne, S. Cohen, J. C. Moreton, Y. J. Colon, L. Chen, R. Clowes, F. X. Coudert, Y. Cui, B. Hou, D. M. D'Alessandro, P. W. Doheny, M. Dinca, C. Sun, C. Doonan, M. T. Huxley, J. D. Evans, P. Falcaro, R. Ricco, O. Farha, K. B. Idrees, T. Islamoglu, P. Feng, H. Yang, R. S. Forgan, D. Bara, S. Furukawa, E. Sanchez, J. Gascon, S. Telalovic, S. K. Ghosh, S. Mukherjee, M. R. Hill, M. M. Sadiq, P. Horcajada, P. Salcedo-Abraira, K. Kaneko, R. Kukobat, J. Kenvin, S. Keskin, S. Kitagawa, K. I. Otake, R. P. Lively, S. J. A. DeWitt, P. Llewellyn, B. V. Lotsch, S. T. Emmerling, A. M. Putz, C. Marti-Gastaldo, N. M. Padial, J. Garcia-Martinez, N. Linares, D. Maspoch, J. A. Suarez Del Pino, P. Moghadam, R. Oktavian, R. E. Morris, P. S. Wheatley, J. Navarro, C. Petit, D. Danaci, M. J. Rosseinsky, A. P. Katsoulidis, M. Schroder, X. Han, S. Yang, C. Serre, G. Mouchaham, D. S. Sholl, R. Thyagarajan, D. Siderius, R. Q. Snurr, R. B. Goncalves, S. Telfer, S. J. Lee, V. P. Ting, J. L. Rowlandson, T. Uemura, T. Iiyuka, M. A. van der Veen, D. Rega, V. Van Speybroeck, S. M. J. Rogge, A. Lamaire, K. S. Walton, L. W. Bingel, S. Wuttke, J. Andreo, O. Yaghi, B. Zhang, C. T. Yavuz, T. S. Nguyen, F. Zamora, C. Montoro, H. Zhou, A. Kirchon and D. Fairen-Jimenez, How Reproducible are Surface Areas Calculated from the BET Equation?, Adv. Mater., 2022, 34(27), e2201502 CrossRef PubMed.
- A. Comotti, S. Bracco, P. Sozzani, S. Horike, R. Matsuda, J. Chen, M. Takata, Y. Kubota and S. Kitagawa, Nanochannels of two distinct cross-sections in a porous Al-based coordination polymer, J. Am. Chem. Soc., 2008, 130(41), 13664–13672 CrossRef CAS.
- H. Furukawa, F. Gandara, Y. B. Zhang, J. Jiang, W. L. Queen, M. R. Hudson and O. M. Yaghi, Water adsorption in porous metal-organic frameworks and related materials, J. Am. Chem. Soc., 2014, 136(11), 4369–4381 CrossRef CAS.
- P. Küsgens, M. Rose, I. Senkovska, H. Fröde, A. Henschel, S. Siegle and S. Kaskel, Characterization of metal-organic frameworks by water adsorption, Microporous Mesoporous Mater., 2009, 120(3), 325–330 CrossRef.
- J. Canivet, A. Fateeva, Y. Guo, B. Coasne and D. Farrusseng, Water adsorption in MOFs: fundamentals and applications, Chem. Soc. Rev., 2014, 43(16), 5594–5617 RSC.
- L. Liu and S. G. Telfer, Systematic ligand modulation enhances the moisture stability and gas sorption characteristics of quaternary metal-organic frameworks, J. Am. Chem. Soc., 2015, 137(11), 3901–3909 CrossRef CAS PubMed.
- A. K. Rappi, C. J. Casewit, K. S. Colwell, W. A. Goddard and W. M. Skid, UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations, J. Am. Chem. Soc., 1992, 114(25), 10024–10035 CrossRef.
- C. Zou, D. R. Penley, E. H. Cho and L.-C. Lin, Efficient and accurate charge assignments via a multilayer connectivity-based atom contribution (m-CBAC) approach, J. Phys. Chem. C, 2020, 124(21), 11428–11437 CrossRef CAS.
- C. Campaná, B. Mussard and T. K. Woo, Electrostatic potential derived atomic charges for periodic systems using a modified error functional, J. Chem. Theory Comput., 2009, 5(10), 2866–2878 CrossRef PubMed.
- E. O. Fetisov, M. S. Shah, J. R. Long, M. Tsapatsis and J. I. Siepmann, First principles Monte Carlo simulations of unary and binary adsorption: CO(2), N(2), and H(2)O in Mg-MOF-74, Chem. Commun., 2018, 54(77), 10816–10819 RSC.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, Comparison of simple potential functions for simulating liquid water, J. Chem. Phys., 1983, 79(2), 926–935 CrossRef CAS.
- L. C. Jacobson, R. M. Kirby and V. Molinero, How Short Is Too Short for the Interactions of a Water Potential? Exploring the Parameter Space of a Coarse-Grained Water Model Using Uncertainty Quantification, J. Phys. Chem. B, 2014, 118(28), 8190–8202 CrossRef CAS.
- M. H. Factorovich, E. Gonzalez Solveyra, V. Molinero and D. A. Scherlis, Sorption isotherms of water in nanopores: relationship between hydropohobicity, adsorption pressure, and hysteresis, J. Phys. Chem. C, 2014, 118(29), 16290–16300 CrossRef CAS.
- R. Stryjek and J. H. Vera, PRSV: An improved Peng-Robinson equation of state for pure compounds and mixtures, Can. J. Chem. Eng., 1986, 64(2), 323–333 CrossRef CAS.
- M. H. Factorovich, V. Molinero and D. A. Scherlis, A simple grand canonical approach to compute the vapor pressure of bulk and finite size systems, J. Chem. Phys., 2014, 140(6), 064111 CrossRef.
- Monte Carlo and Lattice Model Codes for use with SAPT-based force fields, https://schmidt.chem.wisc.edu/software/montecarlosimulationcodes/, (accessed 1 Oct., 2023).
- A. W. Knight, N. G. Kalugin, E. Coker and A. G. Ilgen, Water properties under nano-scale confinement, Sci. Rep., 2019, 9(1), 8246 CrossRef PubMed.
- M. C. Lawrence and M. J. Katz, Analysis of the water adsorption isotherms in UiO-based metal-organic frameworks, J. Phys. Chem. C, 2021, 126(2), 1107–1114 CrossRef.
- A. Zaragoza, M. H. Factorovich and V. Molinero, Multistage condensation pathway minimizes hysteresis in water harvesting with large-pore metal-organic frameworks, Chem. Mater., 2024, 36(2), 708–719 CrossRef CAS.
- Q. Yang, P. Z. Sun, L. Fumagalli, Y. V. Stebunov, S. J. Haigh, Z. W. Zhou, I. V. Grigorieva, F. C. Wang and A. K. Geim, Capillary condensation under atomic-scale confinement, Nature, 2020, 588(7837), 250–253 CrossRef CAS PubMed.
- N. Giovambattista, P. G. Debenedetti and P. J. Rossky, Effect of surface polarity on water contact angle and interfacial hydration structure, J. Phys. Chem. B, 2007, 111(32), 9581–9587 CrossRef CAS.
- P. G. M. Mileo, K. Ho Cho, J. Park, S. Devautour-Vinot, J.-S. Chang and G. Maurin, Unraveling the Water Adsorption Mechanism in the Mesoporous MIL-100(Fe) Metal–Organic Framework, J. Phys. Chem. C, 2019, 123(37), 23014–23025 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Detailed information of MOFs, force field parameters and LGCMC. See DOI: https://doi.org/10.1039/d4lf00354c |
| This journal is © The Royal Society of Chemistry 2025 |