Understanding the evolution of double perovskite band structure upon dimensional reduction

Abstract

Recent investigations into the effects of dimensional reduction on halide double perovskites have revealed an intriguing change in band structure when the three-dimensional (3D) perovskite is reduced to a two-dimensional (2D) perovskite with inorganic sheets of monolayer thickness (n = 1). The indirect bandgap of 3D Cs₂AgBiBr₆ becomes direct in the n = 1 perovskite whereas the direct bandgap of 3D Cs₂AgTlBr₆ becomes indirect at the n = 1 limit. Here, we apply a linear combination of atomic orbitals approach to uncover the orbital basis for this bandgap symmetry transition with dimensional reduction. We adapt our previously established method for predicting band structures of 3D double perovskites for application to their 2D congeners, emphasizing new considerations required for the 2D lattice. In particular, we consider the inequivalence of the terminal and bridging halides and the consequences of applying translational symmetry only along two dimensions. The valence and conduction bands of the layered perovskites can be derived from symmetry adapted linear combinations of halide p orbitals propagated across the 2D lattice. The dispersion of each band is then determined by the bonding and antibonding interactions of the metal and halide orbitals, thus affording predictions of the essential features of the band structure. We demonstrate this analysis for 2D Ag–Bi and Ag–Tl perovskites with sheets of mono- and bilayer thickness, establishing a detailed understanding of their band structures, which enables us to identify the key factors that drive the bandgap symmetry transitions observed at the n = 1 limit. Importantly, these insights also allow us to make the general prediction that direct → indirect or indirect → direct bandgap transitions in the monolayer limit are most likely in double perovskite compositions that involve participation of metal d orbitals at the band edges or that have no metal-orbital contributions to the valence band, laying the groundwork for the targeted realization of this phenomenon.

---

1. Introduction

Dimensional reduction of a three-dimensional (3D) structure to produce lower-dimensional derivatives can generate substantial changes in optoelectronic properties. For example, mechanical exfoliation of transition metal dichalcogenides, such as MoS₂, converts the indirect bandgap of the 3D lattice to a direct bandgap in the two-dimensional (2D) monolayer flake,^1,2 generating unique properties that have triggered numerous fundamental studies and resulted in various applications.^3–5

Dimensional reduction of halide perovskites has also been widely explored. Here, the 3D framework of corner sharing [BX₆]ⁿ⁻ octahedra (B = metal cation, X = halide, Fig. 1A) can easily be converted to lower-dimensional derivatives by replacing the monovalent A-site cations that occupy the small cavities between octahedra with larger organic cations. These large A-site cations partition the perovskite lattice into slabs of varying thickness where the n value of the 2D perovskite counts the number of layers of metal-halide octahedra making up the slabs (Fig. 1B and C).^6,7 Dimensional reduction of the A^IPb^IIX₃ perovskites has long been studied and affords substantial changes in optoelectronic properties, leading to applications for these 2D materials in light emission^8,9 and photovoltaic technologies.¹⁰ More recently, interest has turned to dimensional reduction of halide double perovskites,^11–21 structures that incorporate an ordered arrangement of two distinct cations at the B site, giving the general formula A₂^IBB′X₆.

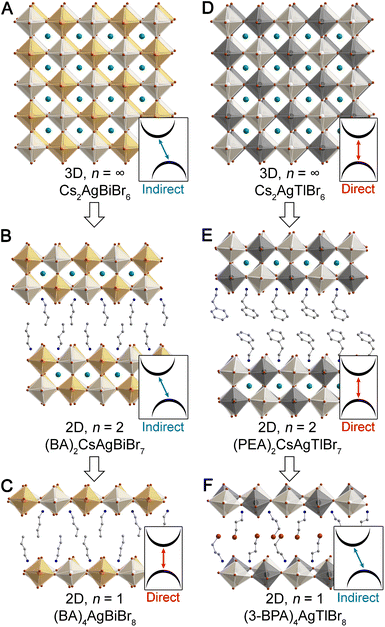Fig. 1 Single-crystal X-ray diffraction structures of the 3D double perovskites Cs₂AgBiBr₆ (ref. 22) (A) and Cs₂AgTlBr₆ (ref. 23) (D), their n = 2 analogues, (BA)₂CsAgBiBr₇ (ref. 13) (B) and (PEA)₂CsAgTlBr₇ (ref. 15) (E), and their n = 1 analogues, (BA)₄AgBiBr₈ (ref. 13) (C) and (3-BPA)₄AgTlBr₈ (ref. 15) (F). (BA = butylammonium, PEA = phenethylammonium, 3-BPA = 3-bromopropylammonium). Insets indicate the direct/indirect nature of the bandgap of each perovskite. Orange, black, white, teal, brown, blue, and gray spheres represent Bi, Tl, Ag, Cs, Br, N, and C atoms, respectively. H and disordered atoms omitted for clarity.

One of the most intriguing findings to emerge from work on double perovskites has been the observation of substantial changes in electronic structure upon dimensional reduction. In contrast to 2D single perovskites, which show band structures analogous to their 3D analogues (albeit with the expected reduction in band dispersion),¹¹ dimensional reduction produces a dramatic shift in bandgap symmetry when the 3D double perovskites Cs₂AgBiBr₆ (ref. 22) and Cs₂AgTlBr₆ (ref. 23) are reduced to monolayer thickness in the n = 1 perovskites.^13,15 We refer to the two k points that define the valence band maximum (VBM) and conduction band minimum (CBM) for a given electronic structure as the bandgap symmetry; a change in the k points of at least one of these band extrema affords a bandgap symmetry transition.

The indirect bandgap of Cs₂AgBiBr₆ (Fig. 1A) has been shown through experiment and theory, and DFT calculations reveal that an analogous indirect gap is maintained in all structures with n ≥ 2. However, the n = 1 Ag–Bi perovskite (Fig. 1C) is calculated to have a direct bandgap. Although electronically distinct from Cs₂AgBiBr₆, we see a similar bandgap symmetry transition with dimensional reduction of Cs₂AgTlBr₆ (Fig. 1D). Here, a direct gap is seen for all structures with n ≥ 2, yet an indirect gap is calculated for the n = 1 Ag–Tl structure (Fig. 1F). Notably, the Ag–In perovskites behave similarly to the isoelectronic Ag–Tl perovskites, with a direct gap calculated for the 3D lattice and an indirect gap calculated for the n = 1 lattice.¹⁵

Layered perovskites typically show distortions not seen in the cubic 3D materials. Calculations on undistorted model Ag–Bi and Ag–Tl systems, obtained by excising slices from the cubic 3D lattice, demonstrate that the changes in band structure are driven by dimensional reduction, rather than by the structural distortions of the layered perovskite lattice.^13,15 However, an understanding of the underlying orbital basis for the bandgap symmetry transitions with dimensional reduction is still lacking. Such insight is critical for assessing the generality of this phenomenon across the rapidly expanding array of double perovskite compositions and for predicting which compositions are likely to feature this effect.

Here, we adapt the linear combination of atomic orbitals (LCAO) approach that we previously developed for 3D double perovskites²⁴ to the 2D n = 1 and 2 derivatives. We describe several important modifications to this analysis that are required for the 2D case and then demonstrate our approach by mapping out the band structures of the undistorted n = 1 and 2 Ag–Bi and Ag–Tl structures, finding good agreement between our predictions and DFT calculations. This work establishes an understanding of the orbital basis of the band structures of the 2D Ag–Bi and Ag–Tl perovskites. We use this understanding to identify two factors that drive the bandgap symmetry transition at the n = 1 limit: (i) the 2D translational symmetry of the layered structures and (ii) the stronger interaction of metal orbitals with terminal halides than with bridging halides. Importantly, our analysis reveals that dimensional reduction will not change the bandgap symmetry for all double perovskite compositions—only for those where metal d orbitals contribute to the band edges or those with no metal orbital character in the valence band.

2. Results

We begin with a brief summary of our previous work²⁴ where we applied an LCAO approach to derive the essential features of 3D double perovskite band structure as these concepts provide a helpful roadmap for this work. For a detailed introduction to the LCAO method applied to solids, the reader is referred to the seminal text by Hoffmann.²⁵

2.1 Key concepts from the LCAO analysis of 3D double perovskites

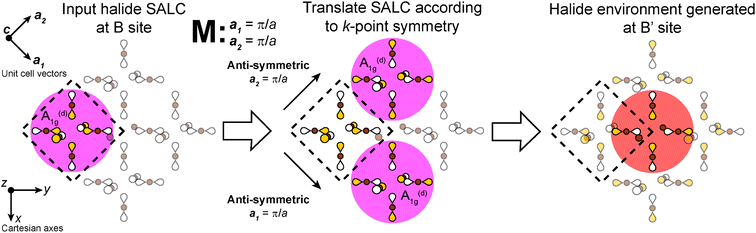
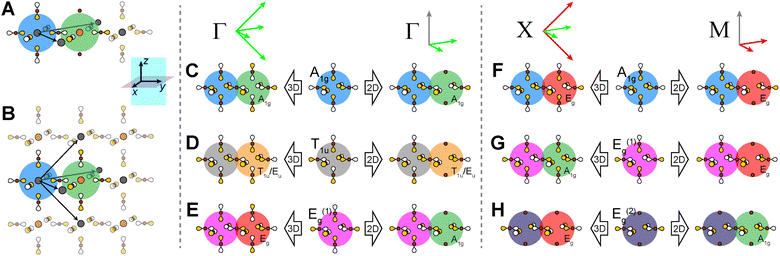
In our analysis of the 3D lattices, we first generated symmetry adapted linear combinations (SALCs) of the six σ-bonding halide p orbitals surrounding the B site of the double perovskite lattice based on the O_h point symmetry of their arrangement (Fig. 2A). Positioning a given SALC about the B site, we then carried out symmetric or antisymmetric translations of this SALC to adjacent B sites according to the translational symmetry rules of the high-symmetry k points of the double perovskite lattice, generating a set of 3D halide Bloch waves. Each Bloch wave preserves the symmetry of the starting SALC at the B site, but the different translational symmetry rules of each k point produce differing symmetries and thus different halide orbital environments at the adjacent B′ site (Fig. 2B). Because the SALC at the B site is unchanging, the bonding/antibonding interactions at the B′ site determine the relative energies of this set of Bloch waves. Thus, the interactions at the B′ site map out the dispersion of the band derived from the starting SALC placed at the B site (Fig. 2C).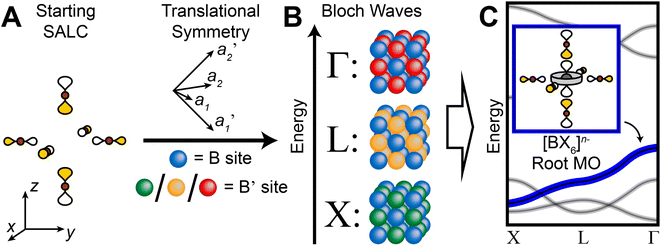

Fig. 2 Outline of the LCAO approach used in this work. A halide SALC (A) is propagated across the lattice generating a series of halide Bloch waves of varying energies (B). Blue spheres represent the unchanging halide orbital environment (halide SALC) at the B site whereas green, yellow, and red spheres represent the different halide orbital environments produced at the B′ site. The energetic ranking of these Bloch waves, including their interactions with B′-site metal orbitals, determines the dispersion of the band derived (C). The metal orbital + starting SALC combination present throughout the band is designated as the root MO of the band (C, inset). One of the E_g halide SALCs for the 3D lattice²⁴ is shown in (A). Brown and gray circles represent halide and metal atoms, respectively. Yellow and white lobes represent the phases of the σ-bonding halide p orbitals and are scaled to give an approximate sense of relative electron density.

In the following, we adapt this analysis to n = 1 and 2 double perovskites, placing particular emphasis on aspects that must be altered or are entirely new for the 2D lattices. Since we previously determined that structural distortions of the perovskite lattice are not the driving force behind the change in band structure observed in the Ag–Bi and Ag–Tl perovskites,^13,15 we perform our analysis on undistorted n = 1 and 2 double perovskites assuming bond lengths and angles equal to those found in the cubic parent 3D double perovskite (Fig. 1A and D). Nevertheless, the band structures derived for these model systems can be used as starting points for forecasting how distortions observed in experimental structures (Fig. 1B, C, E and F) alter band dispersion, as we have demonstrated previously.¹³

Since at least one of the frontier orbitals of the metal cations of both the Ag–Bi and Ag–Tl perovskites are capable of forming strong σ interactions with the surrounding halide p orbitals, the most important features of the conduction and valence bands can be derived by considering only the σ-bonding states. Nevertheless, the methodology presented for the σ-bonding states can be extended to π-bonding states to accommodate cases where π-bonding d_yz/d_xz/d_xy metal orbitals contribute to the band edges. This analysis is provided in ESI Section S6.†

2.2 LCAO analysis for undistorted n = 1 perovskites

2.2.1 SALC derivation. As for the 3D case, we begin by generating SALCs of the six σ-bonding halide p orbitals surrounding the B site of an undistorted n = 1 double perovskite (A₄BB′X₈). However, unlike in the cubic 3D perovskites where the six equivalent halide p orbitals generate O_h point symmetry,²⁴ here, the inequivalence of the two axial (terminal) and four equatorial (bridging) p orbitals gives this configuration D_4h point symmetry. Using group theory, we generate six SALCs with symmetry labels A_1g^(s), A_1g^(d), E_u⁽¹⁾, E_u⁽²⁾, B_1g, and A_2u, where the “s” and “d” superscripts indicate the A_1g SALCs with the appropriate symmetry to interact with s and d_z² B-site metal orbitals, respectively. These SALCs are pictured in Fig. 3 (see ESI Section S3.1† for full derivation).

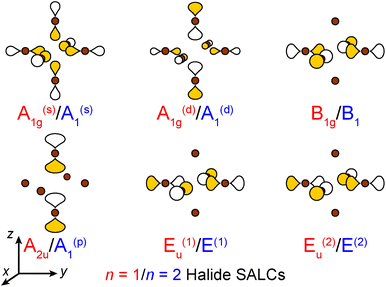Fig. 3 The six σ-bonding halide SALCs for the n = 1 and 2 perovskites with their symmetry labels shown in red and blue, respectively. Brown spheres represent halide atoms. The yellow and white p orbital lobes represent positive and negative phases, respectively and are scaled to give an approximate sense of relative electron density. The two degenerate E_u/E orbitals are drawn as linear combinations of the SALCs with p_x and p_y symmetry (see ESI† for details).

2.2.2 Generating halide Bloch waves. The undistorted n = 1 perovskite has a primitive tetragonal lattice, where two orthogonal lattice vectors (a₁ and a₂) of equal length (a) define translations in the plane of the perovskite sheet, and a third longer vector (c) describes translations to adjacent layers (Fig. 4A). In most layered perovskites, neighboring sheets are separated by large distances and optical^26,27 and theoretical investigations^28,29 have clearly established that these materials have a 2D electronic structure. Therefore, we only consider translations along the two in-plane vectors in our analysis.

Fig. 4 (A) The tetragonal unit cell of an undistorted n = 1 halide double perovskite. Orange, white, brown, and teal spheres represent the B- and B′-site cations, halides, and A-site cations, respectively. (B) The translational symmetry of the high-symmetry k points of a primitive tetragonal lattice. The two different phases of the unit cells are represented in blue and orange. Green and red arrows represent in-phase and out-of-phase translations, respectively, of the starting SALC along the corresponding lattice vector.

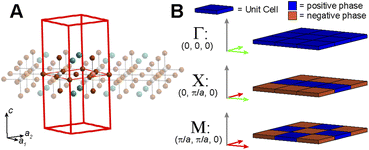
Placing a halide SALC at the B site, we can translate it along a₁ and a₂ to adjacent B sites, thus propagating our starting SALC across the perovskite lattice to generate a halide Bloch wave. We perform these translations either symmetrically (in-phase) or antisymmetrically (out-of-phase) according to the coordinates of the high-symmetry k points of the tetragonal lattice. Bonding/antibonding interactions are maximized at these high-symmetry points, leading to the formation of band extrema. Here, we consider the k points Γ = (0, 0, 0), M = (π/a, π/a, 0), and X = (0, π/a, 0). A coordinate of 0 calls for a symmetric translation of our starting SALC along the corresponding lattice vector whereas a coordinate of π/a calls for an antisymmetric translation (Fig. 4B). Fig. 5 shows a top-down view of the n = 1 perovskite lattice, illustrating the procedure for generating a Bloch wave from a starting SALC of A_1g^(d) symmetry at the M point. Repeating this procedure for each starting SALC in Fig. 3 at the three high-symmetry k points generates 18 halide Bloch waves (Fig. S25–S42†) which are summarized in Fig. 6 by showing the halide orbitals around adjacent B and B′ sites. Note that, unlike in the 3D case, no axial halides are generated at the B′ site by translational symmetry since there are no B sites above or below the B′ sites. This has important consequences for the band structure of the n = 1 perovskites as discussed below.

Fig. 5 Example of the procedure for propagating a halide SALC across the n = 1 perovskite lattice to generate a halide Bloch wave. Here, we begin with an A_1g^(d) SALC at the B site (highlighted in pink) and translate anti-symmetrically (flipping the orbital phases) along the two in-plane unit-cell vectors (a₁ and a₂) according to the coordinates of the M point generating the halide environment at the B′ site (highlighted in red, with E_g point symmetry). The relative size of p orbitals is kept uniform for simplicity. Yellow and white lobes represent positive and negative phases, respectively. Brown spheres represent halide atoms.

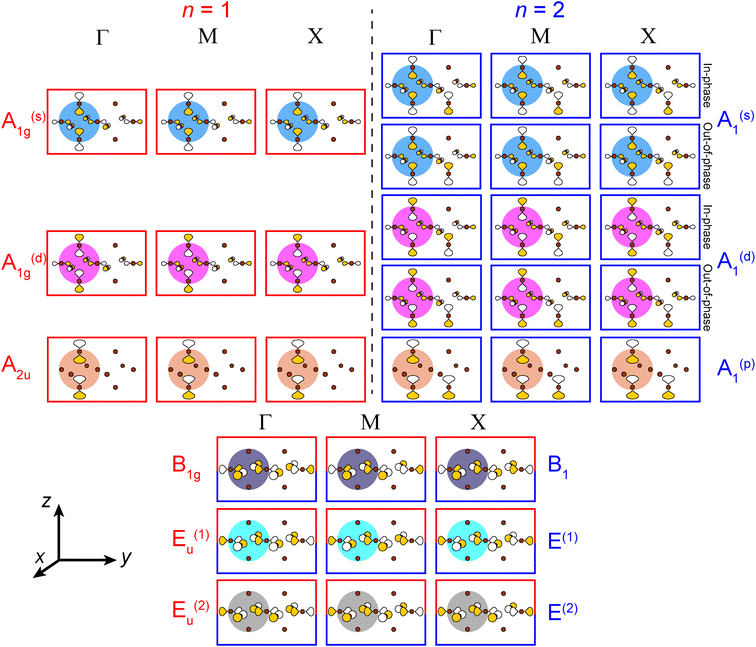Fig. 6 A summary of all unique n = 1 and 2 halide Bloch waves (outlined in red and blue, respectively) at the Γ, M, and X points. Derivations are given in the ESI.† The n = 1 B_1g and E_u^(1,2) Bloch waves have halide orbital environments at the B and B′ sites that are identical to the n = 2 B₁ and E^(1,2) Bloch waves, respectively, and are shown together (red and blue box). Additionally, in cases where the in-phase and out-of-phase combinations of the starting SALC give the same set of n = 2 Bloch waves, we show this set only once. The p orbital lobes are scaled to represent approximate relative electron densities. Yellow and white lobes represent positive and negative phases, respectively. Brown spheres represent halide atoms.

2.2.3 The [BX₆]ⁿ⁻ root molecular orbital (MO). Each set of Bloch waves in Fig. 6 can combine with symmetry-matching orbitals of the B and B′ cations of appropriate energy to generate the bands found in the band structure. From Fig. 6, it is clear that the set of Bloch waves derived from a given starting SALC preserves the symmetry of that SALC at the B site. Thus, the same B-site metal orbital can participate in all three Bloch waves (at Γ, M, and X) and hence, will contribute to the entire band derived from that starting SALC. In contrast, the different translational symmetry rules of each k point generate different halide orbital environments at the B′ site, such that a frontier metal orbital of the B′ cation may have the appropriate symmetry to participate in one but not all of these Bloch waves. We refer to the metal orbital + starting SALC combination that is present throughout a band, which is a [BX₆]ⁿ⁻ molecular orbital (MO), as the “root MO” of this band (Fig. 2C, inset).

It is important to emphasize the distinction we draw between the B- and B′-site cations. Either of the two metal cations of a given double perovskite composition (e.g., Ag⁺ or Bi³⁺ in Cs₂AgBiBr₆) could be considered the B-site or the B′-site cation, depending on which band we are considering. The cation that forms the [BX₆]ⁿ⁻ root MO of the band under consideration (the metal cation enclosed by the starting halide SALC; e.g., Ag⁺) is considered the B-site occupant. The other (i.e., Bi³⁺) is considered the B′-site occupant (the metal cation surrounded by the halide orbitals generated through translational symmetry; Fig. 5). However, if we consider a different band where Bi³⁺ participates in the [BX₆]ⁿ⁻ root MO, the assignment would be reversed: Bi³⁺ and Ag⁺ would be the B- and B′-site cations, respectively. Additionally, in all figures depicting halide Bloch waves, the B and B′ sites are shown on the left and right sides, respectively.

2.2.4 Evaluating orbital interactions. Dimensional reduction will not significantly alter the energies of the B-site metal orbitals, meaning that the same frontier metal orbitals that contribute to the band edges of a given 3D double perovskite will be located at an appropriate energy to participate at the band edges in the 2D double perovskite as well. Furthermore, analogous to the 3D case, we find n = 1 halide SALCs with the correct symmetry to form σ-bonding/antibonding interactions with B-site metal s, p, d_z² and d_x²−y² orbitals (Fig. 3). Therefore, we can determine the root MOs of the valence and conduction bands of a given 2D perovskite by inspecting the band structure of the 3D parent: for a given band, the 2D root MO will consist of the same B-site metal orbital that participates in the root MO of the analogous band in the 3D band structure combined with the n = 1 halide SALC of matching symmetry.

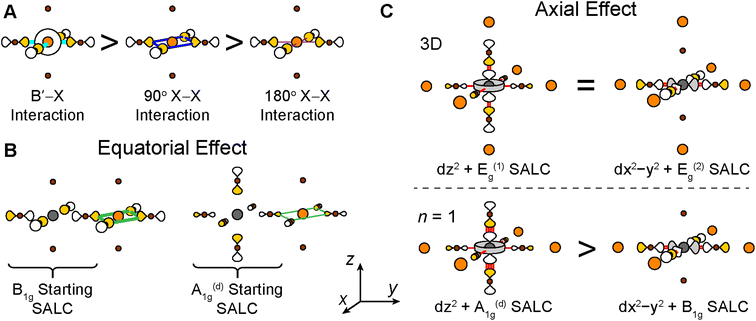
For each band, we identify the three Bloch waves in Fig. 6 (at Γ, M, and X) derived from the halide SALC of the band's root MO. Since these three Bloch waves have identical interactions at the B site, their energetic ranking, and hence the dispersion of the band, is determined by the bonding/non-bonding/antibonding interactions at the B′ site. The strongest interactions are B′–X interactions between a frontier orbital of the B′ cation (with an appropriate energy to participate in the band) and the surrounding halide p orbitals of matching symmetry (Fig. 7A). In the absence of such B′–X interactions, weaker X–X interactions between halide orbitals surrounding the B′ site determine the energy of the Bloch wave (Fig. 7A). Our prior work showed that interactions between adjacent halides positioned at 90° with respect to one another (90° X–X interactions) are more important than those between the more distant halides positioned at 180° with respect to one another (180° X–X interactions),²⁴ so here, we consider only the former.

Fig. 7 (A) Relative strength of the B′–X, 90° X–X, and 180° X–X interactions present at the B′ site. (B) Illustration of the equatorial effect. Green lines indicate bonding 90° X–X interactions and the line thickness indicates that interactions formed in the B_1g-derived Bloch wave are stronger than in the A_1g^(d)-derived Bloch wave. (C) Illustration of the axial effect. The terminal axial halides of the n = 1 structure can interact more strongly with the metal center than the bridging equatorial halides, increasing the energy of the d_z²–A_1g^(d) antibonding combination relative to the d_x²−y²–B_1g antibonding combination (bottom panel). The analogous combinations for the 3D structure are isoenergetic (top panel). The number of red lines denotes the approximate strength of the antibonding interactions. Gray, orange, and brown spheres represent B cations, B′ cations, and halides, respectively. Orbital lobes are shaded to denote relative phases.

2.2.5 The equatorial effect. In the 2D case, it becomes important to consider the relative size of the p orbital lobes involved in bonding/antibonding interactions at the B′ site. For example, the large equatorial halide p orbital lobes generated from the B_1g starting SALC will form much stronger interactions (either with each other or with a B′ metal orbital) than the small equatorial lobes generated from the A_1g^(d) starting SALC (Fig. 7B). Because the 2D translational symmetry of the layered structures does not propagate the axial halide p orbitals of the starting SALC to the B′ sites (Fig. 5), Bloch waves derived from starting SALCs with axial halide contributions (i.e., A_1g^(d)) will form much weaker interactions at the B′ site than those derived from starting SALCs with no axial halide contributions (i.e., B_1g) (Fig. 7B). We refer to this effect as the “equatorial effect”. Note that this effect is not at play in the 3D case where translational symmetry generates all six halide p orbitals around the B′ site, not just the equatorial ones.

2.2.6 The axial effect. The inequivalence of the axial and equatorial halide ligands in the n = 1 structure introduces another subtlety to our n = 1 LCAO analysis. In the octahedral ligand field of the 3D structure, all six halides can form equally strong interactions with the metal center and the d_z² and d_x²−y² orbitals of the B site form equally strong antibonding interactions with the surrounding halides (Fig. 7C, top). However, in the n = 1 structure, the axial halides are not shared between two metal centers and, therefore, can interact more strongly with a B-site metal orbital compared to the equatorial halides that bridge metals. Since the axial halides interact strongly with the d_z² orbital but not at all with the d_x²−y² orbital, the antibonding interaction between the d_z² orbital and the A_1g^(d) SALC will be stronger than that of the d_x²−y² orbital with the B_1g SALC (Fig. 7C, bottom). We refer to this as the “axial effect” and demonstrate its effect on band structure below.

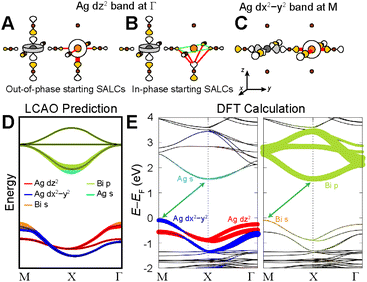
2.3 Case study 1: the Ag–Bi n = 1 perovskite

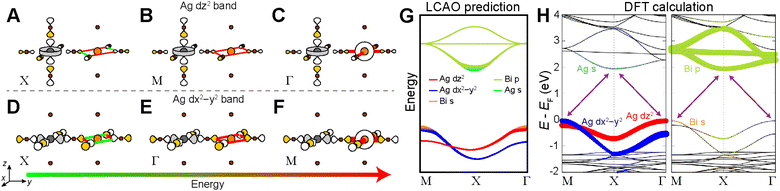
Below, we demonstrate this analysis for the undistorted n = 1 Ag–Bi perovskite. A similar analysis of the structurally analogous but electronically distinct Ag–Tl perovskite can be found in the ESI Section S5.1.†

2.3.1 Predictions for the valence band. The two highest-energy valence bands (VBs) of 3D Cs₂AgBiBr₆ are derived from root MOs that are the antibonding combinations of the Ag d_z² and d_x²−y² orbitals with halide SALCs of the appropriate symmetry. Thus, we expect the [AgBr₆]⁵⁻ unit to form the root MO for the two highest-energy VBs of the 2D lattice as well. Here, the n = 1 A_1g^(d) and B_1g halide SALCs match the symmetry of the Ag d_z² and d_x²−y² orbitals, respectively, so to map out these bands, we will consider the A_1g^(d)- and B_1g-derived Bloch waves shown in Fig. 6, which have the appropriate symmetry at the B site to interact with these Ag d orbitals at all high-symmetry k points.

The three high-symmetry Bloch waves for the Ag d_z² band (where the d_z² orbital participates in the root MO) are shown in Fig. 8A–C, arranged in order of increasing energy from left to right. The highest-energy Bloch wave occurs at Γ, where the 90° interactions between halide p orbitals (90° X–X interactions) are all in-phase at the Bi site, enabling strong σ-antibonding interactions with the filled 6s orbital of Bi³⁺ (Fig. 8C). (Based on the contribution of Bi 6s orbitals to the VBM of Cs₂AgBiBr₆, these states are located at an appropriate energy to participate in the band.)²⁴ The Bi 6s orbitals do not have the required symmetry to contribute at M or X, so we rank these Bloch waves based on the weaker 90° X–X interactions around the Bi site. The antibonding configuration at M (Fig. 8B) and the non-bonding configuration at X (Fig. 8A) give an overall energetic ordering of the k points of Γ > M > X.

Fig. 8 LCAO analysis for the n = 1 Ag–Bi structure. LCAO representations of the Ag d_z² derived valence band (VB) at the X (A), M (B), and Γ (C) points ranked in order of increasing energy from left to right. LCAO representations of the Ag d_x²−y² derived VB at the X (D), Γ (E), and M (F) points ranked in order of increasing energy from left to right. Bonding and antibonding interactions at the B′ site are shown as green and red lines, respectively, and the thickness of each line corresponds to the strength of the interaction. Halide p orbital lobes are scaled to represent approximate relative electron densities and the shading of orbital lobes denote their relative phases. Gray, orange, and brown spheres represent Ag, Bi, and Br atoms, respectively. (G) Predicted band diagram of the n = 1 Ag–Bi structure using our LCAO analysis. (H) DFT band structure of the n = 1 Ag–Bi structure without SOC. The band structure is shown in duplicate where the Ag (left panel) and Bi (right panel) states that compose the bands are represented by colored dots.

Fig. 8D–F shows the three Bloch waves for the Ag d_x²−y² band. Here, the highest energy is found at M where the Bloch wave has the correct symmetry at the B′ site to have antibonding interactions with the Bi 6s orbital (Fig. 8F). The antibonding and non-bonding 90° X–X interactions found at Γ and X, respectively (Fig. 8D and E), yield an overall energetic ordering of the k points of M > Γ > X.

Having predicted the dispersion pattern for the Ag d_z² and d_x²−y² bands, we now must evaluate the relative energies of these two bands. The Bi s orbitals contribute antibonding character to the maxima of both bands. However, due to the equatorial effect (Section 2.2.5), the B_1g-derived Bloch wave of the d_x²−y² band will interact more strongly with the Bi s orbital than the A_1g^(d)-derived Bloch wave of the d_z² band (Fig. 8C and F). Thus, the equatorial effect increases the energy of the d_x²−y² band at M relative to the d_z² band at Γ.

At the same time, the axial effect (Section 2.2.6) pushes the entire d_z² band up in energy relative to the d_x²−y² band. In the absence of the axial effect, the d_z² and d_x²−y² bands would be isoenergetic at the X point where both have non-bonding 90° X–X interactions around the B′ site. Indeed, this is the case in 3D Cs₂AgBiBr₆ (at the L point, see Fig. S15†).²⁴ However, due to the axial effect, we predict that in the n = 1 structure, the Ag d_z² band is higher in energy than the Ag d_x²−y² band at X (Fig. 8G).

Clearly the axial and equatorial effects will compete to determine the location of the VBM in the n = 1 Ag–Bi perovskite; the equatorial effect boosts the maximum of the d_x²−y² band, whereas the axial effect raises the energy of the entire d_z² band. It is not possible to say which effect will dominate using our qualitative model, so for now we will assume that they are equal, generating isoenergetic VBMs at M and Γ. We diagram our predicted band dispersion for the highest energy VBs of the n = 1 Ag–Bi structure in Fig. 8G.

2.3.2 Predictions for the conduction band. The root MOs of the lowest-energy conduction bands (CBs) of Cs₂AgBiBr₆ are derived from Bi 6p orbitals, so for our n = 1 structure, we consider the Bloch waves derived from the E_u^(1,2) and A_2u SALCs, which can interact with the empty Bi p_x/y and p_z orbitals, respectively. Both E_u SALCs generate net non-bonding 90° X–X interactions around the B′ site at Γ and M (Fig. 6), but, at X, the E_u⁽¹⁾ SALC generates an antibonding arrangement, while the E_u⁽²⁾ SALC generates a bonding arrangement, enabling participation of the empty Ag 5s orbital. (Based on the band structure of Cs₂AgBiBr₆ the Ag 5s orbital is at an appropriate energy to participate in the band.)²⁴ Since this band is based on the antibonding Bi p-E_u⁽²⁾ root MO (i.e., antibonding Bi p - halide p interactions are present throughout), the lowest energy point will occur where the B′ site has the most bonding interactions. Therefore, the CBM is formed at X by the E_u⁽²⁾-derived band where Ag s orbitals form bonding interactions with the in-phase arrangement of surrounding halide p orbitals (Fig. 8G). Similarly, the highest point of the E_u⁽¹⁾-derived band also occurs at X, where antibonding 90° X–X interactions at the B′ site are maximized. The full LCAO representations of these bands at the three k points are given in Fig. S18.†

The A_2u SALC involves only the two axial halide p orbitals at the B site, which have no translational symmetry equivalents at the B′ site. As a result, there are no halide orbitals around the B′ sites in the A_2u-derived Bloch waves so all three are isoenergetic, giving a band with no dispersion (Fig. 8G).

2.3.3 Comparison of predictions from LCAO analysis to DFT calculations. Comparing our predicted band diagram of the n = 1 Ag–Bi perovskite (Fig. 8G) to the DFT band structure (Fig. 8H), we find good agreement. The Ag d_z² and dx²−y² VBs follow the predicted patterns of dispersion and we find small contributions from Bi 6s orbitals to the maxima of these bands, as predicted from the LCAO analysis. Importantly, far less Bi s character is observed in the d_z² band at Γ than in the d_x²−y² band at M (see Table S1†), consistent with the expected influence of the equatorial effect (Fig. 8C and F). Furthermore, DFT shows that the Ag d_z² band is higher in energy than the Ag d_x²−y² band at X, consistent with our assessment of the axial effect. These calculations also reveal that the d_x²−y² and d_z² bands reach isoenergetic VBMs at M and Γ, respectively, indicating that the competing axial and equatorial effects have similar magnitudes in this system.

Our predictions for the CB are also in good qualitative agreement with the DFT calculations, which shows two Bi p-based bands that display a large splitting at X and a third that has very little dispersion. It is important to point out that the DFT band structure in Fig. 8H was calculated without accounting for spin-orbit coupling (SOC) because our model is a non-relativistic one, which does not consider SOC effects. However, SOC has a substantial impact on the dispersion pattern of the Bi 6p-based CB and we refer the interested reader to the ESI Section S4† for a discussion of this point.

2.4 LCAO analysis for undistorted n = 2 perovskites

In the sections below, we describe how the analysis outlined above can be extended to n = 2 structures.

2.4.1 SALC derivation. In the n = 2 structure, the inequivalence of the terminal and bridging axial halides (Fig. 1B) lowers the point symmetry of the B site to C_4v. Thus, we generate halide SALCs of the six σ-bonding halide p orbitals surrounding the B site according to this point group (see ESI Section S3.2† for derivation). These SALCs are shown in Fig. 3 and have the symmetry labels A₁^(s), A₁^(d), A₁^(p), B₁, E⁽¹⁾, and E⁽²⁾, where the superscripts “s”, “d”, and “p” designate the A₁ SALCs with the appropriate symmetry to interact with s, d_z², or p_z B-site orbitals, respectively. While these SALCs have different symmetry labels than the n = 1 SALCs, most aspects of their physical descriptions remain unchanged (see ESI Section S3.2†).

2.4.2 In-phase and out-of-phase combinations of SALCs. Propagation of our halide SALCs across the perovskite lattice is complicated in the n = 2 case by the fact that the B sites in the top layer of the n = 2 sheet are not related to those in the bottom layer by translational symmetry (Fig. 9A). Therefore, to generate a halide Bloch wave for the entire lattice, we must use a larger unit cell and input our starting SALC at two B sites, one in the top layer and one in the bottom layer. These two starting SALCs can be either in-phase or out-of-phase with respect to one another (Fig. 9B and C). In cases where the SALC has contributions from both axial and equatorial halide p orbitals (e.g., A₁^(d)), the phase difference between the starting B-site SALCs affects the halide orbital environment at the B′ site and will lead to splitting of the bands generated from the in-phase and out-of-phase combinations at some k points (Fig. 9B). However, the phase difference will not affect bands derived from SALCs with contributions from only axial or only equatorial halide p orbitals (e.g., B₁; Fig. 9C), and here we expect two degenerate bands.

Fig. 9 (A) Unit cell of an n = 2 double perovskite. Orange, white, brown, and teal spheres represent the B- and B′-site cations, halides, and A-site cations, respectively. In-phase and out-of-phase combinations of the A₁^(d) (B) and B₁ (C) halide SALCs. Brown spheres represent Br atoms. Yellow and white shading of the p orbital lobes denotes their relative phase. For simplicity, the relative size of p orbitals is kept uniform. Circled axial halide orbitals highlight the different halide orbital environments generated at the B′ site depending on the phase difference of the starting SALCS (in-phase vs. out-of-phase).

2.4.3 Generating halide Bloch waves. We propagate the in-phase and out-of-phase SALC combinations across the n = 2 lattice using a procedure analogous to that demonstrated in Fig. 5 for the n = 1 lattice (Fig. S16†), generating 24 unique Bloch waves (Fig. S34–S57†) which are summarized in Fig. 6. As in the n = 1 structure, the terminal axial halide is not generated at the B′ site by translational symmetry. However, there is a bridging axial halide at the B′ site, generated by the starting SALC positioned about the B site in the adjacent layer (Fig. 9B; circled). As a result, Bloch waves generated from starting SALCs with axial halide contributions have different halide orbital environments at the B′ site than those generated from the analogous n = 1 starting SALCs, while Bloch waves generated from starting SALCs without axial contributions have the same interactions at the B′ site as their n = 1 analogues (Fig. 6).

2.4.4 The axial and equatorial effects. The axial and equatorial effects are still relevant for the n = 2 structures. However, the magnitude of the equatorial effect will be diminished since the bridging axial halide at the B′ site is generated by the starting SALC (Fig. 9B), and the axial effect will also be less important since one of the axial halides at the B site is now shared with the adjacent B′ site (Fig. 9B). These slight alterations to the axial and equatorial effects are demonstrated in case studies of the n = 2 Ag–Bi perovskite given below and the n = 2 Ag–Tl perovskite given in the ESI Section S5.2.†

2.5 Case study 2: the Ag–Bi n = 2 perovskite

2.5.1 Predictions for the valence band. As for the 3D and n = 1 Ag–Bi perovskites, the two highest VBs in the n = 2 structure are based on the Ag d_z² and d_x²−y² orbitals. We map out the dispersion of these bands using the same procedure as for the n = 1 structure above (see Fig. S17† for full analysis), arriving at the predictions shown in Fig. 10D. Note that there are two d_z² and two d_x²−y² bands, corresponding to the in-phase and out-of-phase combinations of the two starting SALCs. Consistent with our analysis in Section 2.4.2, the two d_x²−y² bands are degenerate at all three k points, but the two d_z² bands split at Γ. Here, for the out-of-phase combination of starting SALCs, translational symmetry generates s-orbital symmetry at the B′ site allowing for strong antibonding interactions with Bi s orbitals (Fig. 10A). In contrast, translational symmetry generates a weakly antibonding configuration of 90° X–X interactions at the B′ site for the in-phase combination of starting SALCs (Fig. 10B).

Fig. 10 LCAO representation of the d_z²- and d_x²−y²-derived valence bands of the n = 2 Ag–Bi structure at Γ (A and B) and M (C), respectively. Bonding and antibonding interactions at the B′ site are shown as green and red lines, respectively, where line thickness indicates the strength of the interaction. Gray, orange, and brown spheres represent Ag, Bi, and Br atoms, respectively. Halide p orbital lobes are scaled to represent approximate relative electron densities and their shading denotes their relative phase. (D) Predicted band structure of the n = 2 Ag–Bi structure. Double black lines indicate degenerate bands. (E) DFT band structure for the n = 2 Ag–Bi structure calculated without SOC. The band structure is shown in duplicate where the Ag (left panel) and Bi (right panel) states that compose the bands are represented by colored dots.

Due to the equatorial effect, Bi s orbitals introduce more antibonding character to the d_x²−y² band at M (Fig. 10C) than to the d_z² band at Γ (Fig. 10A), raising the energy of the VBM at M relative to Γ. At the same time, the axial effect raises the energy of the entire d_z² band relative to the d_x²−y² band. The magnitudes of these effects are expected to be reduced compared to the n = 1 case (Section 2.4.4) though it is difficult to predict the relative magnitudes of these reductions. Thus, our predictions in Fig. 10D assume that they are reduced by the same amount and therefore, remain equally important (as in the n = 1 analogue), resulting in isoenergetic VBMs at M and Γ.

2.5.2 Predictions for the conduction band. The halide Bloch waves for our Bi p-based CBs are essentially identical to those for the n = 1 analogues (Fig. S18†) and we predict the same pattern of band dispersion as in the n = 1 perovskite (Fig. 10D), although here, each band is doubly degenerate corresponding to the in-phase and out-of-phase combinations of the starting SALCs.

2.5.3 Comparison of predictions to DFT. We see good qualitative agreement between our predicted band structure and the DFT band structure calculated without SOC (Fig. 10E). Importantly, DFT shows that the VBM at M is 180 meV higher in energy than at Γ indicating that the equatorial effect is more important than the axial effect in the n = 2 structure (in contrast to the n = 1 analogue where isoenergetic VBMs occurred at both M and Γ).

3. Discussion

The approach presented above affords an understanding of the molecular-level interactions that determine the band structure of the 2D Ag–Bi perovskites (and Ag–Tl perovskites; see ESI Section S5†), positioning us to identify the factors driving the change in bandgap symmetry observed at the n = 1 limit in both systems.

3.1 3D vs. 2D translational symmetry

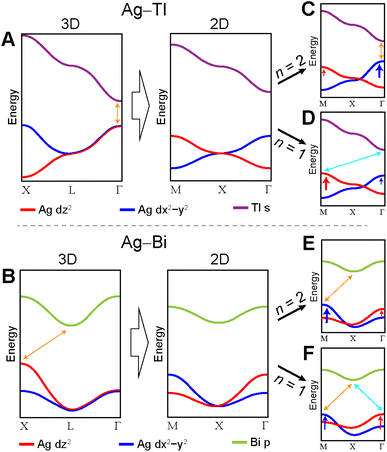
The switch from 3D to 2D translational symmetry plays an important role in the bandgap symmetry transition of the n = 1 Ag–Bi and Ag–Tl perovskites. Translational symmetry of the layered perovskites is defined in terms of two orthogonal unit-cell vectors lying in the xy plane (Fig. 11A). These same two vectors describe translations within the xy plane of the 3D lattice, while an identical set rotated by 90° define translations in the yz plane (Fig. 11B, see Fig. S19† for vector derivation).

Fig. 11 Consequences of 3D vs. 2D translational symmetry. Translational symmetry vectors of the 2D (A) and 3D (B) double perovskite lattices. Bloch waves generated at the 3D and 2D Γ points for the A_1g (C), T_1u (D), and E_g⁽¹⁾ (E) starting SALCs. Bloch waves generated at the 3D X point and 2D M point for the A_1g (F), E_g⁽¹⁾ (G), and E_g⁽²⁾ (H) starting SALCs. Red and green vectors represent antisymmetric and symmetric translations, respectively. The color of the shaded circle behind each B′ site indicates the symmetry of the halide environment generated there by translational symmetry (green = A_1g, yellow = T_1u/E_u, red = E_g). For simplicity, here we use the halide SALCs of the 3D lattice and the size of orbital lobes is kept uniform. Gray, orange, and brown spheres represent B-site cations, B′-site cations, and halide atoms, respectively, and the shading of p orbital lobes represents relative phase.

The simplified band diagrams shown in Fig. 12A and B (which omit the influence of the axial and equatorial effects) demonstrate how the differences in 3D and 2D translational symmetry result in distinct band structures for the 3D and 2D lattices in the Ag–Tl and Ag–Bi systems. Specifically, we observe very different dispersion patterns for the Ag d-based VBs of the 3D and 2D lattices, but the dispersion patterns of the lowest-lying Tl s- and Bi p-derived CBs are identical in the 3D and 2D structures. In the sections below, we explain the origins of these differences.

Fig. 12 Diagrams illustrating the dispersion of the valence and conduction bands of the Ag–Tl and Ag–Bi perovskites. Panels A and B demonstrate the changes in dispersion of the Ag d_z² and d_x²−y² bands caused by switching from 3D to 2D translational symmetry. Panels C–F illustrate the changes in the Ag d_z² and d_x²−y² bands caused by the axial (red arrows) and equatorial (blue arrows) effects. Note that these diagrams represent simplified band structures; some bands and orbital contributions are omitted for clarity.

3.1.1 Differences between the E_g and A_1g/T_1u SALCs. We begin by considering the A_1g, E_g, and T_1u SALCs of the 3D lattice (Fig. 11; note that for simplicity, here we only consider one of the three degenerate T_1u SALCs; see the ESI Section S7† for details). For the A_1g and T_1u SALCs, the halide orbital environment in the xy and yz (and xz) planes is equivalent (i.e., within each plane, all halide p orbitals are in-phase for the A_1g SALC, and for the T_1u SALC, each halide p orbital is in-phase with one of its 90°-adjacent neighbors and out-of-phase with the other). As a result, both 3D (defined in the xy and yz planes) and 2D (defined in the xy plane) translational symmetry produce equivalent sets of Bloch waves from these starting SALCs (i.e., these Bloch waves have halide orbital environments at the B′ site with analogous symmetry for the 2D and 3D case; Fig. S20 and S21.†) These Bloch waves give rise to metal s- and p-derived bands, respectively, explaining why the dispersion patterns of the Tl s- and Bi p-derived CBs in Fig. 12A and B do not change upon dimensional reduction. (See the ESI Section S7† for an explanation of why this holds despite the splitting of the 3D T_1u SALCs at the X point in the 3D lattice and in the 2D lattice.).

In contrast to the A_1g and T_1u SALCs, the two E_g SALCs do not have equivalent halide orbital environments in the xy and yz planes. For example, in the E_g⁽¹⁾ SALC, the halide p orbitals in the xy plane are all in-phase whereas in the yz plane adjacent halide p orbitals are out-of-phase with one another. As a result, translation of the E_g SALCs across the xy plane of the 2D lattice produces a set of Bloch waves distinct from those generated by translation across the xy and yz planes of the 3D lattice (i.e., some of the 2D Bloch waves have halide orbital environments at the B′ site with a different symmetry than for their respective 3D analogues, Fig. S22 and S23†). Therefore, bands derived from these Bloch waves will show different patterns of dispersion in the 2D and 3D lattices, explaining why the Ag d_z²- and d_x²−y²-based VBs shown in Fig. 12A and B change upon dimensional reduction. Below, we give several examples to illustrate why the E_g SALCs produce different patterns of band dispersion in the 3D and 2D lattices.

3.1.2 Example 1: differences at the Γ point. In both the 2D and 3D lattice, the Γ point calls for symmetric translations along all vectors. As described above, for the A_1g starting SALC, this produces equivalent Bloch waves in the 3D and 2D lattices where the halide orbital environments at the B′ site have A_1g symmetry in both cases (Fig. 11C). Similarly, the T_1u starting SALC produces equivalent Bloch waves with T_1u/E_u symmetry at the B′ site for both the 3D and 2D lattices (Fig. 11D, note that the E_u symmetry label is the 2D analogue to the 3D T_1u symmetry label, see ESI Section S7†). However, for the E_g⁽¹⁾ starting SALC, 2D and 3D translational symmetry yield inequivalent Bloch waves (Fig. 11E). In the 3D case, we find E_g symmetry at the B′ site where the axial halide p orbitals (along the z axis) are out-of-phase with the equatorial p orbitals (in the xy plane), thus generating net antibonding 90° X–X interactions. However, since 2D translational symmetry does not generate these axial orbitals at the B′ site, we are left with A_1g symmetry in the 2D case (where the 90° X–X interactions are bonding). This is a clear result of the difference in halide orbital environment between the xy and yz planes of the E_g⁽¹⁾ SALC described in Section 3.1.1. Because of this difference for the E_g⁽¹⁾ SALC, it matters that only xy translational symmetry exists in the 2D case, unlike in the A_1g and T_1u cases. We can easily see the effect on band dispersion by considering the Ag–Tl perovskite band structures where the patterns of dispersion of the Ag d-based VBs is determined by the 90° X–X interactions around the Tl site (see ESI S5†). As shown in Fig. 12A, in the 3D lattice, the Ag d_z²-derived VB reaches its maximum at Γ, but in the 2D lattice, this band's minimum lies at Γ.

3.1.3 Example 2: differences at the 3D X and 2D M points. The 3D X point calls for symmetric translations in the xy plane (green arrows in Fig. 11) and antisymmetric translations in the yz plane (red arrows in Fig. 11), producing a halide orbital environment with E_g symmetry at the B′ site in the A_1g-derived Bloch wave (Fig. 11F). Since the A_1g SALC has equivalent halide orbital environments in the xy and yz planes, antisymmetric translations in either plane have the same effect. Thus, in the 2D case where there is no translational symmetry in the yz plane, antisymmetric translations in the xy plane (at the M point) produce a Bloch wave equivalent to the 3D case with E_g symmetry at the B′ site (Fig. 11F). However, for the E_g SALCs, the halide orbital environments in the xy and yz planes are not equivalent (Fig. 11G). As a result, antisymmetric translation of the E_g⁽¹⁾ SALC in the yz plane produces a Bloch wave for the 3D lattice with A_1g symmetry (bonding 90° X–X interactions) at the B′ site, but antisymmetric translation in the xy plane produces a Bloch wave for the 2D lattice with E_g symmetry (antibonding 90° X–X interactions) at the B′ site. As a result, for the Ag–Tl perovskites where the dispersion patterns of the Ag d bands are determined by the 90° X–X interactions at the B′ site, the d_z² band of the 3D lattice has its minimum at the X point but in the 2D lattice this same band has its maximum at the analogous M point (Fig. 12A). Similarly, antisymmetric translation of the E_g⁽²⁾ SALC in the yz plane produces a Bloch wave with E_g symmetry (antibonding 90° X–X interactions) at the B′ site, but when this antisymmetric translation moves to the xy plane in the 2D lattice, we find A_1g symmetry (bonding 90° X–X interactions) at the B′ site (Fig. 11H), explaining why the dispersion patterns of the 3D and 2D d_x²−y² bands diverge at the 3D X point and the 2D M point in the Ag–Tl perovskites (Fig. 12A).

3.2 The axial effect vs. the equatorial effect

We have shown that 2D translational symmetry alters the dispersion pattern of the Ag d-orbital-based VBs in both the Ag–Tl and Ag–Bi perovskites, but that alone does not explain the change in bandgap symmetry at the n = 1 limit. Below, we add the influence of the axial and equatorial effects to show how the interplay of these three factors can explain the observed bandgap transitions.

3.2.1 The Ag–Tl case. In contrast to the band structure of the 3D Ag–Tl perovskite, the 2D translational symmetry in the 2D analogues moves the maximum of the Ag d_z² band away from the Γ point (to M) and generates only one maximum in the Ag d_x²−y² band at Γ (Fig. 12A). The competing axial and equatorial effects then determine whether the dz² band at M or the d_x²−y² band at Γ will form the VBM. In the n = 2 structure, the equatorial effect dominates (see ESI Section S5.2†) forming a d_x²−y²-based VBM at Γ and resulting in a direct bandgap analogous to the 3D system (Fig. 12C). However, in the n = 1 system, the two terminal axial halides strengthen the axial effect (see ESI Section S5.1†), thereby shifting the d_z² band up in energy and moving the VBM to M to give an indirect bandgap between M and Γ (Fig. 12D). Thus, in the Ag–Tl system, the direct-to-indirect bandgap transition observed at the n = 1 limit occurs because 2D translational symmetry moves the maximum of the d_z² band away from the Γ point and then the axial effect raises the energy of this band, making it the VBM.

3.2.2 The Ag–Bi case. In the Ag–Bi perovskites, 2D translational symmetry generates a d_x²−y²-based VBM at M while moving the maximum of the d_z² band to the Γ point (Fig. 12B). Once again, the equatorial effect dominates in the n = 2 perovskite, so the VBM is formed by the d_x²−y² band at M (Section 2.5), resulting in an indirect bandgap analogous to that of the 3D structure (Fig. 12E). However, as the axial effect becomes more pronounced in the n = 1 analog, the d_z² band rises in energy (Section 2.3), generating an isoenergetic VBM at Γ (Fig. 12F). Thus, similar to the Ag–Tl system, the substantial change in VB dispersion observed in the n = 1 Ag–Bi perovskite occurs because 2D translational symmetry moves the maximum of the d_z² band to the Γ point and then the axial effect raises the energy of this band so that it forms a VBM.

Although our LCAO analysis predicts an abrupt change in bandgap symmetry at the n = 1 limit of the Ag–Bi perovskite and agrees with the DFT calculations presented here, these results do not capture the direct bandgap at Γ that we previously reported for the n = 1 perovskite.¹³ This is because our theory is a non-relativistic one, which cannot account for SOC. Including SOC in the DFT calculations substantially alters the dispersion of the Bi p-based CBs, generating a CBM at Γ that is 150 meV lower than that at X and producing a direct gap at Γ (Fig. S3†). Thus, a direct gap is attained at the n = 1 limit due to the effects of dimensional reduction and SOC.

3.2.3 The Ag–Sb case. It is important to point out that the delicate balance between the axial and equatorial effects is highly composition dependent. Indeed, in the n = 1 Ag–Sb structure (which is isoelectronic to the Ag–Bi composition) the equatorial effect dominates because Sb 5s orbitals are higher in energy than Bi 6s orbitals (due to relativistic contraction of 6s orbitals) and therefore, contribute more heavily to the VBM (Table S1†). This increases the importance of the equatorial effect and generates a d_x²−y²-based VBM at M (with a halide environment of A_1g symmetry at the B′ site, which can interact with the Sb 5s orbital). Thus, unlike the Ag–Bi perovskites, here all structures have indirect bandgaps between analogous k points, despite the change in VB dispersion patterns with dimensional reduction (Fig. S4†). (Note that SOC, which is a relativistic effect, does not have a large effect on the Sb 5p-based CBs of the n = 1 Ag–Sb perovskite so the CBM is at X, as predicted [see ESI Section S4†].)

3.3 The role of metal d orbitals and d-orbital symmetry

The interplay of 2D translational symmetry, the equatorial effect, and the axial effect is critical for determining the bandgap symmetry of the n = 1 and 2 Ag–Bi and Ag–Tl perovskites. However, from the discussion in Sections 2.2.5, 2.2.6, and 3.1 it is clear that all three of these factors are relevant for bands derived from B-site metal d_z² and d_x²−y² orbitals but not for those based on B-site metal s and p orbitals. In the ESI Section S6,† we extend our analysis to π-bonding states, finding that 2D translational symmetry, the equatorial effect, and the axial effect are also important considerations for bands based on the π-bonding metal d_yz, d_xz, and d_xy orbitals. This allows us to make the more general statement that any band based on a B-site metal d orbital is expected to undergo changes in dispersion pattern upon dimensional reduction. We also demonstrate in ESI Section S8† that d orbital contributions at the B′ site can lead to different patterns of dispersion in the 2D and 3D lattices.

The changes to metal d-orbital-derived bands observed upon dimensional reduction are all rooted in the inequivalence of the halide orbital environments found in the xy and yz planes of the 3D halide SALCs with d-orbital symmetry that compose these bands (Section 3.1). Thus, we can make the more general statement that a band derived from any 3D SALC having different halide orbital environments in the xy and yz planes will undergo a change in dispersion pattern upon dimensional reduction, thereby encompassing bands to which no metal orbitals contribute. A number of SALCs, including all of those with d-orbital symmetry, meet this requirement, but most relevant to consider are those capable of forming the most antibonding 90° X–X interactions (the 3D E_g^(1,2) and T_1g SALCs and a subset of their 2D analogues: the A_1g^(d), B_1g, and A_2g SALCs; see ESI Sections S6.5 and S9†) because these will constitute the highest VBs of double perovskite compositions where both B-site cations have low-lying HOMOs and do not contribute to the valence band edges. However, note that such perovskites will have relatively flat bands, making changes in bandgap symmetry is less significant than in compositions where both B-site metals contribute.

To summarize, we expect that only double perovskite compositions in which metal d orbitals contribute at the band edges or in which no metal orbitals contribute to the VB are likely to display a change in bandgap symmetry upon dimensional reduction. Indeed, (CH₃NH₃)₂TlBiBr₆, a double perovskite where only metal s and p orbitals contribute to the band edges, shows no substantial changes in band structure upon dimensional reduction (Fig. S24†).

4. Conclusions

The direct-to-indirect bandgap transition of 3D Cs₂AgTlBr₆, as it is thinned to a monolayer in the n = 1 2D perovskite, as well as the indirect-to-direct bandgap transition as 3D Cs₂AgBiBr₆ is dimensionally reduced to an n = 1 2D perovskite have been shown through DFT calculations.^13,15 However, an explanation for why these bandgap symmetry transitions occur only in certain double perovskite compositions has been lacking. Achieving such an understanding may yield guidelines on which double perovskite compositions are likely to show such a transition with dimensional reduction.

To address this question, and to improve our understanding of this emerging family of materials, we have developed an LCAO analysis for 2D double perovskites that uncovers the orbital basis for the changes in bandgap symmetry with dimensional reduction. We describe several considerations needed for the LCAO analysis of 2D double perovskites. In particular, we highlight the importance of (a) 2D translational symmetry, which results in the axial (terminal) halides at the B site not being translated to the B′ site, and (b) the “axial effect”, which describes the consequences of stronger interactions between the B-site metal orbitals and the axial (terminal) halides compared to those with the equatorial (bridging) halides. These considerations, irrelevant for the LCAO analysis of 3D perovskites,²⁴ form the basis for the change in bandgap symmetry upon dimensional reduction from the 3D Cs₂AgBiBr₆ and Cs₂AgTlBr₆ perovskites to the 2D analogues. Specifically, 2D translational symmetry moves the maximum of the Ag d_z²-based valence band (VB) away from its location in the 3D analogue, and the axial effect raises the energy of this band, creating a new valence band maximum (VBM).

Our analysis does not account for spin-orbit coupling (SOC), which can change the band dispersion patterns of certain double perovskite compositions, as discussed in the ESI Section S4.† Nevertheless, our simple treatment can capture many of the relevant factors that dictate the bandgaps of layered double perovskites, and importantly, helps develop the intuition of synthetic chemists targeting new double perovskite compositions that show this bandgap symmetry transition. We therefore highlight the key take-away from our analysis: only double perovskite compositions that involve participation of metal d orbitals at the band edges or that have no metal-orbital contributions to the VB are expected to display changes in bandgap symmetry upon dimensional reduction due to the inequivalent halide orbital environments found in the xy and yz planes of the halide SALCs involved in these cases. Such a bandgap symmetry transition is a necessary, though not sufficient, condition for a direct → indirect or an indirect → direct bandgap transition.

Similarly, the change in bandgap symmetry observed at the monolayer limit of MoS₂ has been traced to differences in axial and equatorial interactions. Here, electronic states comprised of orbitals with large axial components (perpendicular to the plane of the 2D sheets, like Mo d_z²) have strong interlayer interactions and therefore undergo a large energetic perturbation upon exfoliation. In contrast, states based on orbitals with electron density primarily in the xy plane of the 2D sheet (like Mo d_x²−y² orbitals) have weak interlayer interactions and will not be significantly affected by exfoliation.³⁰ Thus, the inequivalence of metal d-orbital interactions in the axial and equatorial directions drives the indirect-to-direct bandgap transition upon dimensional reduction observed in MoS₂, similar to our findings for double perovskites presented here.

This study lays the groundwork for using dimensional reduction as a predictable means of changing the direct/indirect nature of the bandgap in other double perovskite compositions.

Data availability

Symmetry-Adapted Linear Combinations of atomic orbitals (SALCs)/Bloch waves derived through the analysis presented here and band structures from DFT calculations are available in the ESI.†

Author contributions

The 2D LCAO analysis was developed by B. A. C. with contributions from all authors. L. L. performed the DFT calculations. The manuscript was written by B. A. C. and H. I. K. with contributions from all authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Science Foundation (NSF; DMR2102306) and the Brown Science Foundation. B. A. C. acknowledges support from an NSF graduate research fellowship (DGE-114747) and the Evelyn McBain award from Stanford Chemistry. A. C. S. acknowledges support from the NSF (DMR2102306) and the John Stauffer Stanford Graduate Fellowship. The computational work was supported by the Dutch Research Council (NWO) under Grant OCENW.M20.337. L. L. also acknowledges funding by the Bavarian State Ministry of Science and the Arts through the Elite Network of Bavaria, the German Research Foundation through SFB840 B7, and computational resources provided by the Bavarian Polymer Institute.

Notes and references

1. A. Splendiani, L. Sun, Y. Zhang, T. Li, J. Kim, C.-Y. Chim, G. Galli and F. Wang, Emerging Photoluminescence in Monolayer MoS₂, Nano Lett., 2010, 10, 1271–1275.
2. K. F. Mak, C. Lee, J. Hone, J. Shan and T. F. Heinz, Atomically Thin MoS₂: A New Direct-Gap Semiconductor, Phys. Rev. Lett., 2010, 105, 136805.
3. D. Jariwala, V. K. Sangwan, L. J. Lauhon, T. J. Marks and M. C. Hersam, Emerging Device Applications for Semiconducting Two-Dimensional Transition Metal Dichalcogenides, ACS Nano, 2014, 8, 1102–1120.
4. S. Manzeli, D. Ovchinnikov, D. Pasquier, O. V. Yazyev and A. Kis, 2D transition metal dichalcogenides, Nat. Rev. Mater., 2017, 2, 17033.
5. T. F. Jaramillo, K. P. Jørgensen, J. Bonde, J. H. Nielsen, S. Horch and I. Chorkendorff, Identification of Active Edge Sites for Electrochemical H₂ Evolution from MoS₂ Nanocatalysts, Science, 2007, 317, 100–102.
6. D. B. Mitzi, Templating and structural engineering in organic–inorganic perovskites, J. Chem. Soc., Dalton Trans., 2001, 1–12,  10.1039/b007070j.
7. B. Saparov and D. B. Mitzi, Organic−Inorganic Perovskites: Structural Versatility for Functional Materials Design, Chem. Rev., 2016, 116, 4558–4596.
8. T. Ishihara, Optical properties of PbI-based perovskite structures, J. Lumin., 1994, 60–61, 269–274.
9. M. D. Smith, B. A. Connor and H. I. Karunadasa, Tuning the Luminescence of Layered Halide Perovskites, Chem. Rev., 2019, 119, 3104–3139.
10. I. C. Smith, E. T. Hoke, D. Solis-Ibarra, M. D. McGehee and H. I. Karunadasa, A Layered Hybrid Perovskite Solar-Cell Absorber with Enhanced Moisture Stability, Angew. Chem., Int. Ed., 2014, 53, 11232–11235.
11. N. R. Wolf, B. A. Connor, A. H. Slavney and H. I. Karunadasa, Doubling the Stakes: The Promise of Halide Double Perovskites, Angew. Chem., Int. Ed., 2021, 60, 16264–16278.
12. L. M. Castro-Castro and A. M. Guloy, Organic-Based Layered Perovskites of Mixed-Valent Gold(I)/Gold(III) Iodides, Angew. Chem., Int. Ed., 2003, 42, 2771–2774.
13. B. A. Connor, L. Leppert, M. D. Smith, J. B. Neaton and H. I. Karunadasa, Layered Halide Double Perovskites: Dimensional Reduction of Cs₂AgBiBr₆, J. Am. Chem. Soc., 2018, 140, 5235–5240.
14. L. Mao, S. M. L. Teicher, C. C. Stoumpos, R. M. Kennard, R. A. DeCrescent, G. Wu, J. A. Schuller, M. L. Chabinyc, A. K. Cheetham and R. Seshadri, Chemical and Structural Diversity of Hybrid Layered Double Perovskite Halides, J. Am. Chem. Soc., 2019, 141, 19099–19109.
15. B. A. Connor, R.-I. Biega, L. Leppert and H. I. Karunadasa, Dimensional reduction of the small-bandgap double perovskite Cs₂AgTlBr₆, Chem. Sci., 2020, 11, 7708–7715.
16. L.-Y. Bi, Y.-Q. Hu, M.-Q. Li, T.-L. Hu, H.-L. Zhang, X.-T. Yin, W.-X. Que, M. S. Lassoued and Y.-Z. Zheng, Two-dimensional lead-free iodide-based hybrid double perovskites: crystal growth, thin-film preparation and photocurrent responses, J. Mater. Chem. A, 2019, 7, 19662–19667.
17. E. T. McClure, A. P. McCormick and P. M. Woodward, Four Lead-free Layered Double Perovskites with the n = 1 Ruddlesden–Popper Structure, Inorg. Chem., 2020, 59, 6010–6017.
18. M. L. Aubrey, A. Saldivar Valdes, M. R. Filip, B. A. Connor, K. P. Lindquist, J. B. Neaton and H. I. Karunadasa, Directed assembly of layered halide perovskite heterostructures as single crystals, Nature, 2021, 597, 355–359.
19. P. Vishnoi, J. L. Zuo, X. Li, D. C. Binwal, K. E. Wyckoff, L. Mao, L. Kautzsch, G. Wu, S. D. Wilson, M. G. Kanatzidis, R. Seshadri and A. K. Cheetham, Hybrid Layered Double Perovskite Halides of Transition Metals, J. Am. Chem. Soc., 2022, 144, 6661–6666.
20. J. Xue, Z. Wang, A. Comstock, Z. Wang, H. H. Y. Sung, I. D. Williams, D. Sun, J. Liu and H. Lu, Chemical Control of Magnetic Ordering in Hybrid Fe–Cl Layered Double Perovskites, Chem. Mater., 2022, 34, 2813–2823.
21. D. C. Binwal, P. P. Mudoi, D. P. Panda and P. Vishnoi, Molybdenum chloride double perovskites: dimensionality control of optical and magnetic properties, Chem. Sci., 2023, 14, 3982–3989.
22. A. H. Slavney, T. Hu, A. M. Lindenberg and H. I. Karunadasa, A Bismuth-Halide Double Perovskite with Long Carrier Recombination Lifetime for Photovoltaic Applications, J. Am. Chem. Soc., 2016, 138, 2138–2141.
23. A. H. Slavney, L. Leppert, A. Saldivar Valdes, D. Bartesaghi, T. J. Savenije, J. B. Neaton and H. I. Karunadasa, Small-Band-Gap Halide Double Perovskites, Angew. Chem., Int. Ed., 2018, 57, 12765–12770.
24. A. H. Slavney, B. A. Connor, L. Leppert and H. I. Karunadasa, A pencil-and-paper method for elucidating halide double perovskite band structures, Chem. Sci., 2019, 10, 11041–11053.
25. R. Hoffmann, Solids and Surfaces: A Chemist's View of Bonding in Extended Structures, Wiley-VCH, 1988.
26. T. Ishihara, J. Takahashi and T. Goto, Optical properties due to electronic transitions in two-dimensional semiconductors (C_nH_2n+1NH₃)₂PbI₄, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 11099–11107.
27. T. Ishihara, X. Hong, J. Ding and A. V. Nurmikko, Dielectric Confinement Effect for Exciton and Biexciton States in PbI₄-Based Two-Dimensional Semiconductor Structures, Surf. Sci., 1992, 267, 323–326.
28. L. Pedesseau, D. Sapori, B. Traore, R. Robles, H.-H. Fang, M. A. Loi, H. Tsai, W. Nie, J.-C. Blancon, A. Neukirch, S. Tretiak, A. D. Mohite, C. Katan, J. Even and M. Kepenekian, Advances and Promises of Layered Halide Hybrid Perovskite Semiconductors, ACS Nano, 2016, 10, 9776–9786.
29. M. D. Smith, L. Pedesseau, M. Kepenekian, I. C. Smith, C. Katan, J. Even and H. I. Karunadasa, Decreasing the Electronic Confinement in Layered Perovskites through Intercalation, Chem. Sci., 2017, 8, 1960–1968.
30. J. E. Padilha, H. Peelaers, A. Janotti and C. G. Van de Walle, Nature and evolution of the band-edge states in MoS₂: From monolayer to bulk, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 205420.

---

Footnote

† Electronic supplementary information (ESI) available: Computational methods, supplementary discussion and figures. See DOI: https://doi.org/10.1039/d3sc03105e

---