 Open Access Article
Open Access ArticleExploring the potential of natural orbital functionals
Mario
Piris
 *ab
*ab
aDonostia International Physics Center (DIPC), Euskal Herriko Unibertsitatea (UPV/EHU), 20018 Donostia, Spain. E-mail: mario.piris@ehu.eus
bIKERBASQUE, Basque Foundation for Science, 48013 Bilbao, Spain
First published on 10th October 2024
Abstract
In recent years, Natural Orbital Functional (NOF) theory has gained increasing significance in quantum chemistry, successfully addressing one of the field's most challenging problems: providing an accurate and balanced description of systems with strong electronic correlation. The quest for NOFs that strike the delicate balance between computational tractability and predictive accuracy represents a holy grail for researchers. Today, NOFs provide an alternative formalism to both density functional and wavefunction-based methods, with their appeal rooted in a wonderfully simple conceptual framework. This perspective outlines the basic concepts, strengths and weaknesses, and current status of NOFs, while offering suggestions for their future development.
1 Introduction
In recent decades, we have witnessed significant advances in hardware and software that have greatly enhanced our ability to simulate molecules and materials with increasing numbers of atoms. This progress has opened new avenues in scientific research, enabling the exploration of molecular dynamics, material properties, and chemical reactions on unprecedented scales. As a result, the fields of computational chemistry and materials science are undergoing a transformative phase, promising groundbreaking discoveries and innovations. Much of this success can be credited to the development of density functional approximations, which provide reasonable results at modest computational costs.Density functional theory (DFT) was established1 by Hohenberg and Kohn (HK), with practical implementations relying on the Kohn–Sham (KS) formulation.2 In the KS approach, the unknown kinetic energy functional as a functional of the electron density is avoided by introducing a reference system of non-interacting electrons described by a single Slater determinant. This difference highlights issues, particularly from the correlation kinetic energy, posing a significant challenge in current density functionals. While local density and generalized gradient approximations are commonly used, they often fail to describe strong electron correlations. Hybrid-exchange functionals and range-separated interactions have been practical solutions to this problem, showing improved performance, although failures persist.3,4 Today, there is a plethora of empirical and non-empirical parametrized density functionals,5 but this extensive parametrization often limits their applicability to specific systems and phenomena, deviating from a physically grounded modeling approach.6,7
The exact solution of the time-independent non-relativistic Schrödinger equation can be achieved by the full configuration interaction (FCI) method, which accounts for all possible electronic configurations based on a one-particle basis, the spin-orbitals. However, FCI scales exponentially with the number of orbitals, making methods based on approximate wavefunctions more practical for solving the many-body problem, despite the progress made with the density matrix renormalization group technique.8 Currently, the coupled-cluster wavefunction with single, double, and perturbative triple excitations9 is considered the “gold standard” in quantum chemistry, with efficient and nearly linear-scaling implementations.10,11 Nevertheless, this method still demands significant computational resources as the system size increases and is unsatisfactory for systems with strong static correlation due to its single Hartree–Fock reference character.
There is no universal consensus on the distinction between static and dynamic electron correlation, and the transition between them is gradual. Static correlation generally involves a limited number of close-lying orbitals, usually the frontier orbitals near the Fermi level. The wavefunction in such cases is a mixture of configuration state functions, each with appreciable weight. In contrast, dynamic correlation involves a very large number of configurations, each with a small weight. The most interesting chemistry—such as systems with partially broken bonds, transition states for bond breaking, transition metal compounds, compounds of strongly electronegative first-row atoms, large conjugated systems, electronically excited states, etc.—requires a balanced treatment of both static and dynamic correlation. Presently, the most reliable approaches to address this are multireference methods, such as the complete active space self-consistent field (CASSCF)12 and its combination with second-order perturbation theory (CASPT2).13 Unfortunately, multireference methods still suffer from high computational costs and sensitivity to active space selection, especially for a large number of strongly correlated orbitals. Furthermore, while incorporating dynamic correlation through perturbative corrections improves the accuracy of absolute energies, it does not improve the quality of the reference. Achieving results that include all electron correlation at once requires a comprehensive optimization process, which becomes computationally prohibitive for multireference-perturbative methods.
Reduced density matrix (RDM)-based methods offer alternative formalisms to both density functional and wavefunction-based approaches. It has long been known14 that the energy of a system with at most two-body interactions is an exact linear functional of the two-particle RDM (2RDM), the only functional we know with certainty. Today, realistic variational 2RDM calculations are possible,15 but they remain computationally expensive. A dramatic reduction in computational scaling can be achieved by further reducing the complexity of the fundamental variable, specifically by using the one-particle reduced density matrix (1RDM).
The existence of a functional of the 1RDM16–18 is already implicit in the original HK theorem.19 However, the existence of the functional alone does not allow us to determine its analytical expression in a general manner. While the Levy formulation17 can reveal the explicit form of the exact functional for certain model systems,20,21 it remains impractical for computational purposes. This limitation has driven the development of approximate functionals, most of which are formulated in the natural orbital (NO) representation,22 where the 1RDM is diagonal. The spectral decomposition of the 1RDM allows the functional to be expressed in terms of the NOs and their occupation numbers (ONs), thereby defining it as a natural orbital functional (NOF).
This perspective is intended for a general audience, emphasizing the fundamental and practical aspects of NOF approximations. Rather than delving into detailed computational procedures and specific system results, it provides insights into the current state of the field and outlines future directions. For a comprehensive historical overview of the formulation and evolution of NOFs, readers are referred to the recent review article by the author.23
2 The method behind approximate NOFs
The Hamiltonian operator of an N-electron system consists of both one- and two-electron components. Consequently, the energy of an electronic system can be determined by accessing the 1RDM and 2RDM, represented as Γ and D, respectively: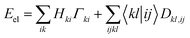 | (1) |
Assuming we can determine the universal functional Vee[Γ], it becomes necessary to impose certain restrictions on the allowable 1RDMs to ensure a physically valid ground-state energy.24 These restrictions require that the 1RDM originate from an N-particle quantum state that is antisymmetric with respect to the exchange of identical electrons, a property known as N-representability. A crucial aspect of N-representability is its connection to either a pure or ensemble state. In 1963, Coleman established25 the conditions for ensuring the ensemble N-representability of Γ, and these are relatively straightforward to implement. In contrast, the more recent systematic approach to deriving pure-state N-representability conditions for the 1RDM,26,27 has proven extremely complex to implement.
For a considerable time, it was widely believed that pure and ensemble universal functionals were equivalent within their shared domain of pure-state N-representable 1RDMs.18,28 However, recent research29 has shown that the ensemble functional is actually the lower convex envelope of the pure functional. Fortunately, the equivalence of pure and ensemble energy functionals on the set of v-representable 1RDMs was confirmed recently.30 Consequently, we can focus on physical electronic systems in their ground states under an external potential v(r), where pure and ensemble functionals are indistinguishable, and consider only ensemble constraints during the energy minimization process to satisfy N-representability conditions.
Disappointingly, analytically determining Vee[Γ] remains a formidable challenge. Despite significant efforts, this goal has yet to be achieved, necessitating the use of approximations for Vee. To approximate the unknown energy functional, one can use the exact functional form (1) in the NO representation, with a 2RDM constructed using a reconstruction functional D[ni, nj, nk, nl], namely,
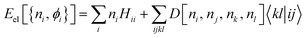 | (2) |
The approximate functional (2) clearly retains dependence on the 2RDM,31 meaning it is necessary to ensure not only the N-representability of the 1RDM but also the N-representability of the functional itself.32 Specifically, the reconstructed D[ni, nj, nk, nl] must satisfy the same N-representability conditions as an unreconstructed D (ref. 33) to guarantee the existence of a compatible N-electron system for the functional.
It has often been assumed, incorrectly, that approximate functionals do not encounter N-representability issues because the 1RDM conditions were believed to be sufficient. Although some functionals, like Müller's,34 appear well-formulated and accurate for certain systems, they often violate fundamental N-representability conditions. This has exposed that many currently used approximate functionals35–37 fail to meet functional N-representability criteria.38–40
Two procedures can be envisioned to derive Eel[{ni, ϕi}]: the so-called top-down and bottom-up methods.41 In the top-down approach, an approximate N-particle wavefunction is proposed in the NO representation, with the expansion coefficients explicitly expressed in terms of the ONs. This method directly yields an approximate functional that is N-representable by construction. Although this approach is straightforward, its success has been limited to a single case beyond the Hartree–Fock approximation: PNOF5.42,43
In contrast, the bottom-up approach involves proposing D[ni, nj, nk, nl] without relying on an N-particle state. The functional is then constructed by incrementally incorporating the set of N-representability conditions33 into the proposed 2RDM reconstruction. Since the complete set of N-representability conditions for the 2RDM involves higher-order RDMs, only those conditions directly related to the 2RDM itself can be effectively applied. Specifically, the (2,2)-positivity conditions are used, which require the two-electron density matrix, the electron–hole density matrix, and the two-hole density matrix to be positive semidefinite. Consequently, we can never be entirely certain that the functional is fully N-representable, with the exception of PNOF5, which was derived using this method before its generating wavefunction was identified. However, the other functionals obtained via the bottom-up method can be considered approximately N-representable, as only some of the necessary N-representability conditions are imposed. The more conditions imposed on the 2RDM, the closer the resulting energy (2) is to the exact energy.
Given the implicit dependence of approximate functionals on the 2RDM, it is more accurate to classify Eel[{ni, ϕi}] as a NOF rather than as a 1RDM functional. Ultimately, these functionals are only comprehended within the NO representation, including even the well-established functional derived from the Löwdin–Shull wavefunction44 with a chosen phase combination, which accurately describes closed-shell two-electron systems. In this context, NOFs can be regarded as approximate energy expressions derived from an approximate quantum state, with certainty when using the top-down method and with high confidence when employing the bottom-up method. A significant consequence of this is that energy is not invariant under unitary transformations of the orbitals, resulting in the absence of a generalized Fockian when working with approximate functionals.45 This property can only be guaranteed by the exact 1RDM functional, which can be defined in any representation, not just that of the NOs.
A systematic application of the bottom-up approach, using an explicit two-index approximation46 of the two-particle cumulant,47,48 has resulted in the development of a series of JKL-only functionals known as PNOFi (i = 1–7),49–55 where J, K, and L represent Coulomb, exchange, and exchange-time-inversion integrals, respectively.56 These functionals have been particularly successful in capturing static electron correlation,57 especially those based on electron pairing,58 which closely match results from accurate wavefunction-based methods for small systems by also accounting for dynamic electron correlation within intrapair interactions.
The missing dynamic electron correlation can be addressed through perturbative corrections.59–62 However, while this approach primarily improves energies relative to reference NOF values, it does not enhance the quality of the NOs and ONs. Fully correlated NOs and ONs requires a more comprehensive strategy, such as the global NOF (GNOF).63 GNOF achieves a balanced description of dynamic and static correlations, and its strong agreement with accurate wavefunction-based methods in both relative and absolute energies further underscores its reliability.
Minimizing a NOF requires adhering to the orthonormality constraints for the NOs, while the ONs must meet both ensemble N-representability conditions and Löwdin normalization. For NOFs based on electron pairing, additional conditions are imposed, which inherently ensure normalization. This setup results in a constrained optimization problem, typically tackled by optimizing the energy separately with respect to ONs and NOs, since simultaneous optimization of all variables has been shown to be inefficient for approximations.64 Currently, open-source codes like DoNOF65,66 efficiently handle this problem and support GPU acceleration via implementations in modern programming languages such as Python and Julia. These codes provide various features, including geometry optimization, natural and canonical representations of molecular orbitals, computation of ionization potentials and electric moments, perturbative corrections for dynamic correlation, NOF-based ab initio molecular dynamics, and excited state calculations.
3 Assessment and future directions
NOFs can accurately treat strongly correlated systems,67–71 while requiring less computational effort than multiconfigurational wavefunction-based methods and coupled cluster theories. Unlike multireference methods such as CASPT2, NOFs are not sensitive to the selection of the active space or prone to instabilities due to changes in active space orbitals. In typical NOF calculations, all electrons are correlated across all available orbitals within a given basis set, an approach that is currently unfeasible for large systems using existing wavefunction-based methods.NOFs effectively address a broader spectrum of systems72–76 than density functionals, which are limited by their single-reference nature, frequently achieving chemical accuracy.63,77 They are particularly effective in complex scenarios such as bond-breaking and bond-forming reactions,78–81 as well as in transition metal chemistry.82,83 PNOFs based on electron pairing have been especially successful in capturing static electron correlation84 and are the only functionals to date capable of accurately determining the correct number of electrons in the fragments resulting from homolytic dissociations,85–87 thereby eliminating delocalization errors.88
Despite these advantages, the application of NOFs faces several challenges, with computational expense being a significant one. A primary issue is the need to optimize NOs at the molecular orbital level, unlike density functional calculations where optimized orbitals are derived from solving the Kohn–Sham equations in the atomic orbital basis. Optimizing NOs at the molecular level requires a four-index transformation to convert atomic orbital electron repulsion integrals into molecular orbital integrals. Although this transformation is only performed once during occupancy optimization, it must be repeated each time the orbitals change, making NO optimization a particularly time-consuming step in the energy minimization process.
To enhance efficiency, various strategies have been employed. Parallelizing key sections of the code responsible for the four-index transformation has led to significant performance improvements. For certain NOFs, summing over NO indices separately has reduced computational costs by enabling feasible integral-direct formalism calculations,89 decreasing memory demands, and facilitating the use of efficient techniques such as integral screening and the fast multipole method. Additionally, the resolution of identity approximation has been employed66 to further reduce arithmetic and memory scaling, enabling the application of NOF approximations to larger molecular systems of general chemical interest.83
Another key factor influencing computational efficiency is the optimization procedure itself, despite recent efforts.90,91 Over the past two decades, various implementations with varying degrees of effectiveness have emerged. While advances in optimizing ONs have improved efficiency,92 optimizing NOs still requires substantial improvements to make NOF-based methods competitive with density functional approximations. The iterative diagonalization procedure45 represented a significant advancement by generating a generalized pseudo-Fockian, but its efficiency is constrained by the lack of an exact prescription for its diagonal elements and the absence of effective techniques to accelerate convergence in the final stages.
An established alternative to orbital optimization through diagonalization is orbital rotations.93 In this approach, orthonormal orbitals are rotated relative to each other using an orthogonal transformation defined by a skew matrix, which specifies the independent rotation parameters. Consequently, the energy becomes a function of these rotation parameters, with its gradients dictated by the off-diagonal elements of the pseudo-Fockian. This eliminates the need for diagonal elements, enabling the use of trust-region methods,94,95 which provide accurate nonlinear approximation models in each iteration. However, as system size increases, these conventional techniques become increasingly costly. Given the advantages of each approach, combining methods can accelerate the optimization of NOs. Yet, to achieve robust convergence at a reasonable cost, it is evident that we must look beyond traditional techniques and leverage innovative optimization methods. Additionally, to further reduce the scaling of orbital optimization, solving the problem in the atomic orbital basis, as is usually done in self-consistent field methods, is essential.
Another difficulty to consider in any functional theory is spin. Since the electronic Hamiltonian commutes with the total spin squared (S2) and one of its components, typically Sz, its eigenvectors must also be eigenvectors of these spin operators. Some methodologies to address this challenge use spin-unrestricted approaches, which bypass the requirement for approximate functionals to fully exhibit all symmetries. In these methodologies, the number of spin-up and spin-down electrons is fixed, but spin contamination is allowed. Relaxing the constraint on total spin conservation can improve size consistency and accuracy in energy predictions for molecular dissociations, among other scenarios. Nevertheless, spin-unrestricted methodologies often involve non-physical interpretations.
In the absence of an external field, total spin invariance implies that the ground state of a many-electron system forms a multiplet, a mixed quantum state encompassing all possible Sz values. One approach to addressing the spin issue is to focus solely on the high-spin component of the multiplet. Extensions of NOF theory to high-spin multiplet states have been reported,96–98 demonstrating some positive outcomes for atoms and molecules. However, no approximation currently exists that can accurately describe each component of the multiplet individually.
A more comprehensive strategy, without focusing on the specifics of each component, is to treat the multiplet as a whole.99,100 This approach centers on the mixed-spin state with the highest multiplicity (2S + 1 = NI + 1), corresponding to the quantum number S = NI/2, where NI denotes the number of unpaired electrons. A key feature of this formulation is the zero average spin projection across the ensemble, which enables 2RDM reconstructions that conserve spin and allows for the application of the machinery developed for singlet states. The results from this approach, which contrasts with conventional methods that emphasize the high-spin component or break spin symmetry, are promising.101 However, in some systems, additional correlation for unpaired electrons is still necessary,82,83 and simulating individual states remains crucial, especially in cases where the multiplet components are no longer degenerate.
In the context of NOF calculations, the general formulation of analytic energy gradients with respect to nuclear motion facilitates the efficient computation of equilibrium geometries.100,102 These gradients can be obtained through straightforward evaluation, eliminating the need for linear response theory or iterative procedures. However, calculating the analytic Hessian requires knowledge of NOs and ONs at the perturbed geometry, which can only be obtained by solving coupled-perturbed equations.103 Consequently, computing second-order energy derivatives is significantly more demanding in terms of storage and computational time compared to evaluating gradients, making numerical differentiation of analytical gradients more efficient than direct analytical evaluation of the Hessian. This has led to the development of codes that use numerical Hessian calculations to find equilibrium geometries and calculate harmonic vibrational frequencies.65 Nevertheless, it remains highly desirable to develop more efficient techniques to characterize critical points on potential energy surfaces, including saddle points, especially for large systems.
The ability to compute gradients analytically also makes ab initio molecular dynamics (AIMD) simulations using NOF-based methods practical.104 The strategy involves calculating nuclear forces on-the-fly during molecular dynamics, eliminating the need for predefined interatomic potentials, which can be problematic in chemically complex systems with evolving bonding patterns. In such cases, density functional-based AIMDs are often inadequate, while multi-reference methods are costly and may introduce energy discontinuities due to instabilities from changes in active-space orbitals. In addition, NOF-based AIMD offers a distinct edge over existing methods: by tracking the real-time evolution of the NOs along with their ONs, we can observe the dynamic evolution of the electronic structure. Indeed, the unique NO representation adapts dynamically during the trajectory, adjusting to the most favorable nuclear interactions at each step, making it especially valuable for monitoring real-time changes in bonding patterns. Since a reaction mechanism involves the sequence of bond formation and breaking, the time evolution of NOs is the ideal approach for insightful descriptions of reaction mechanisms. Currently, only implementations based on the Born–Oppenheimer approximation are available; however, in the future, non-adiabatic molecular dynamics will be necessary for cases involving strong couplings between two or more potential energy surfaces, which require a quantum treatment of the nuclei.
The most significant achievements of NOFs have so far been in describing ground states, while developing a robust theoretical framework for accurately addressing excited states, both charged (EνN±1 − E0N) and neutral (EνN − E0N), remains an ongoing challenge. Research has mainly focused on the energies of vertical excitations, with only a few studies addressing adiabatic transitions for charged excitations. For neutral excitations, the problem remains unresolved, as a description of the excited state independent of the ground state is still needed. Progress has been made using time-dependent theory within the adiabatic linear response framework105–107 and extending 1RDMFT to ensemble states with fixed weights w.108,109 However, both approaches still require more efficient minimization schemes to achieve significant success.
Current vertical excitation calculations rely on the ground state and vary depending on the excitation operator used to generate either charged or neutral states. Charged excitations are typically addressed using the extended Koopmans' theorem (EKT),110,111 while neutral excitations employ Rowe's excitation operator formalism.112 In both methods, the coefficients defining these excited states are derived from the first- and second-order RDMs of the ground state. NOF-EKT provides satisfactory results for lower ionization potentials (IPs), but its accuracy diminishes for higher IPs.113–116 Recent advancements have improved IP accuracy and effectively addressed band gap opening in various systems,117,118 although some inaccuracies persist in photoemission spectra. Conversely, NOF-EKT offers an unsatisfactory description of electron affinities, though these can be estimated using the inverse of the IP of the corresponding anionic species, computed at the experimental geometry of the neutral species.115 On the other hand, neutral excitations within the extended random-phase approximation (ERPA)119 have recently led to the development of various NOF-ERPA methods,120 which have produced very promising results, comparable to high-level CI methods but at significantly lower computational costs, and substantially outperform those obtained with time-dependent density functional theory. The accuracy of vertical excitation calculations is expected to improve in parallel with advancements in ground-state NOFs, as well as with enhanced implementations to better handle cases involving degeneracy of ONs.
A promising research direction is the extension of NOFs to periodic systems. Previously, some attempts were made using very basic functionals for polymers121 and solids,122,123 where translational symmetry allowed NOs to be represented as Bloch states. Other studies have focused on model systems such as the Hubbard model124 or systems consisting solely of hydrogen atoms.68–70 The most significant achievement to date is demonstrating the viability of NOFs in cases where density functionals struggle, particularly in treating strong correlations, including Mott insulators. Consequently, there is a heightened focus on developing NOF-based methods that can effectively tackle the design and analysis of strongly correlated materials.125
One unresolved issue is the treatment of dispersion interactions. Although some attempts have been made in the past,50JKL-only functionals face significant challenges with these systems. Employing non-JKL functionals with more complex dependencies seems necessary,126 but this approach increases the computational cost of NOFs and detracts from their inherent simplicity. Current alternatives include incorporating perturbative corrections,61 using empirical treatments similar to those in DFT, or potentially improving functionals through machine learning. The latter has already shown promise in 1RDM-based electronic structure calculations,127 in DFT,128,129 and in 1RDMFT for bosons.130 By training on ab initio data, more accurate approximations could be achieved. Nevertheless, a key challenge for these functionals is generalization. Alternatively, machine learning could be employed as a phenomenological predictive tool, directly forecasting observables from large datasets or computational results by establishing intricate connections. However, this approach does not facilitate the rationalization of structure–property relationships from first principles, highlighting the important distinction that prediction does not equate to understanding.131
Finally, an encouraging avenue of research is the integration of NOFs into quantum computing algorithms. Quantum computing already holds the potential for significant advantages over classical methods in electronic structure calculations. However, current quantum processors have limited capabilities, so NOFs could help minimize the quantum resources required. Reducing the cost of quantum simulations for many-electron problems has been demonstrated with 2RDM-based algorithms.132,133 Since 1RDM measurements require sampling of significantly fewer elements than 2RDM measurements, NOFs are expected to result in substantial savings in circuit executions.
4 Conclusions
Over the 40 years since the first NOF appeared, significant progress has been made, and the development of NOFs has experienced a substantial boost in the last two decades. Nowadays, NOFs offer a valuable alternative formalism to both density functional and wavefunction-based methods for studying strongly correlated systems. They have greatly enhanced our understanding of molecular electronic structure, molecular dynamics, spectroscopic properties, and other related aspects. Nonetheless, these functionals are still in their infancy in some respects. For example, while progress has been made in extending them to the relativistic regime,134 further development is needed; and much remains to be done in areas such as the treatment of solvent effects and long-range dispersion interactions, which are crucial for biological systems. Nevertheless, just a few years ago, it seemed unthinkable that we would be able to correlate 360 electrons in 900 orbitals today.135Purists argue that current NOFs are not the exact functional of the 1RDM and lack key properties, such as invariance under unitary transformations of the orbitals. Given the current state of knowledge, finding an analytical expression for the exact 1RDM functional seems unlikely. However, we can aim to develop a sufficiently universal NOF approximation for physical electronic systems that captures as many properties as possible, including those related to N-representability. Our goal is to obtain the right answers for the right reasons. Today, functionals like GNOF have already demonstrated the ability to handle arbitrary electronic systems with any spin value, independent of the external potential, while providing a balanced description of both dynamic and static correlations.
NOF-based methods can be considered “black box” approaches because they do not require the definition of an active space. However, their main drawback remains the computational cost in comparison to density functional calculations. To achieve robust convergence at a reasonable cost, we must go beyond traditional techniques, employing innovative optimization methods and, if possible, using the atomic orbital representation, as done in conventional self-consistent field methods. With the advent of artificial intelligence, it is highly likely that more accurate approximations will be achieved for a wide range of electronic systems. Nevertheless, it is important to remember that we are primarily theorists, not mere predictors, even though our models must still be capable of providing predictive insights.
Data availability
No primary research results, software or code have been included and no new data were generated or analysed as part of this review.Author contributions
The author conceived, researched, and wrote this perspective.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support comes from the Eusko Jaurlaritza (Basque Government), Ref.: IT1584-22 and from the Grant No. PID 2021-126714NB-I00, funded by MCIN/AEI/10.13039/501100011033.Notes and references
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef
.
- W. Kohn and L. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef
.
- A. J. Cohen, P. Mori-Sánchez and W. Yang, Chem. Rev., 2012, 112, 289–320 CrossRef CAS PubMed
.
- H. Kruse, L. Goerigk and S. Grimme, J. Org. Chem., 2012, 77, 10824–10834 CrossRef CAS PubMed
.
- S. Lehtola, C. Steigemann, M. J. T. Oliveira and M. A. L. Marques, SoftwareX, 2018, 7, 1–5 CrossRef
.
- A. D. Becke, J. Chem. Phys., 2022, 156, 214101 CrossRef CAS PubMed
.
- A. M. Teale, T. Helgaker, A. Savin, C. Adamo, B. Aradi, A. Arbuznikov, P. W. Ayers, E. J. Baerends, V. Barone, P. Calaminici, E. Cancès, E. A. Carter, P. K. Chattaraj, H. Chermette, I. Ciofini, T. D. Crawford, F. D. Proft, J. F. Dobson, C. Draxl, T. Frauenheim, E. Fromager, P. Fuentealba, L. Gagliardi, G. Galli, J. L. Gao, P. Geerlings, N. Gidopoulos, P. M. W. Gill, P. Gori-Giorgi, A. Görling, T. Gould, S. Grimme, O. Gritsenko, H. J. A. Jensen, E. R. Johnson, R. O. Jones, M. Kaupp, A. M. Köster, L. Kronik, A. Krylov, S. Kvaal, A. Laestadius, M. Levy, M. Lewin, S. B. Liu, P. F. Loos, N. T. Maitra, F. Neese, J. P. Perdew, K. Pernal, P. Pernot, P. Piecuch, E. Rebolini, L. Reining, P. Romaniello, A. Ruzsinszky, D. R. Salahub, M. Scheffler, P. Schwerdtfeger, V. N. Staroverov, J. W. Sun, E. Tellgren, D. J. Tozer, S. B. Trickey, C. A. Ullrich, A. Vela, G. Vignale, T. A. Wesolowski, X. Xu and W. T. Yang, Phys. Chem. Chem. Phys., 2022, 24, 28700–28781 RSC
.
- F. Verstraete, T. Nishino, U. Schollwöck, M. C. Bañuls, G. K. Chan and M. E. Stoudenmire, Nat. Rev. Phys., 2023, 5, 273–276 CrossRef
.
- M. Urban, J. Noga, S. J. Cole and R. J. Bartlett, J. Chem. Phys., 1985, 83, 4041–4046 CrossRef CAS
.
- C. Riplinger and F. Neese, J. Chem. Phys., 2013, 138, 034106 CrossRef
.
- C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, J. Chem. Phys., 2013, 139, 134101 CrossRef PubMed
.
- B. O. Roos, Adv. Chem. Phys., 2007, 69, 399–445 CrossRef
.
- K. Andersson, P. A. Malmqvist, B. O. Roos, A. J. Sadlej and K. Wolinski, J. Phys. Chem., 1990, 94, 5483–5488 CrossRef CAS
.
- K. Husimi, Proc. Phys.-Math. Soc. Jpn., 1940, 22, 264–314 Search PubMed
.
- D. A. Mazziotti, Chem. Rev., 2012, 112, 244–262 CrossRef CAS PubMed
.
- T. L. Gilbert, Phys. Rev. B: Solid State, 1975, 12, 2111–2120 CrossRef
.
- M. Levy, Proc. Natl. Acad. Sci. U. S. A., 1979, 76, 6062–6065 CrossRef CAS
.
- S. M. Valone, J. Chem. Phys., 1980, 73, 1344–1349 CrossRef
.
- R. A. Donnelly and R. G. Parr, J. Chem. Phys., 1978, 69, 4431–4439 CrossRef CAS
.
- A. J. Cohen and P. Mori-Sánchez, Phys. Rev. A, 2016, 93, 042511 CrossRef
.
- T. S. Müller, W. Töws and G. M. Pastor, Phys. Rev. B, 2018, 98, 045135 CrossRef
.
- P. O. Löwdin, Phys. Rev., 1955, 97, 1474–1489 CrossRef
.
- M. Piris, Adv. Quantum Chem., 2024, 90, 1–52 CrossRef
.
-
A. J. Coleman, in Reduced-Density-Matrix Mechanics: with applications to many-electron atoms and molecules, ed. D. A. Mazziotti, John Wiley and Sons, Hoboken, New Jersey, USA, 2007, ch. 1, vol. 134, pp. 1–9 Search PubMed
.
- A. J. Coleman, Rev. Mod. Phys., 1963, 35, 668–687 CrossRef
.
- A. a. Klyachko, J. Phys.: Conf. Ser., 2006, 36, 72–86 CrossRef
.
- M. Altunbulak and A. Klyachko, Commun. Math. Phys., 2008, 282, 287–322 CrossRef
.
- T. T. Nguyen-Dang, E. V. Ludeña and Y. Tal, J. Mol. Struct.: THEOCHEM, 1985, 120, 247–264 CrossRef CAS
.
- C. Schilling, J. Chem. Phys., 2018, 149, 231102 CrossRef PubMed
.
- O. V. Gritsenko and K. Pernal, Phys. Rev. A, 2019, 100, 012509 CrossRef CAS
.
- R. A. Donnelly, J. Chem. Phys., 1979, 71, 2874–2879 CrossRef CAS
.
-
M. Piris, in Many-Body Approaches Differ. Scales a Tribut. to N. H. March Occas. His 90th Birthd., ed. G. G. N. Angilella and C. Amovilli, Springer, New York, 2018, ch. 22, pp. 261–278 Search PubMed
.
- D. a. Mazziotti, Phys. Rev. Lett., 2012, 108, 263002 CrossRef PubMed
.
- A. M. K. Müller, Phys. Lett. A, 1984, 105, 446–452 CrossRef
.
- S. Sharma, J. K. Dewhurst, N. N. Lathiotakis and E. K. U. Gross, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 201103(R) CrossRef
.
- M. A. L. Marques and N. N. Lathiotakis, Phys. Rev. A, 2008, 77, 032509 CrossRef
.
- D. R. Rohr, K. Pernal, O. V. Gritsenko and E. J. Baerends, J. Chem. Phys., 2008, 129, 164105 CrossRef PubMed
.
- M. Rodríguez-Mayorga, E. Ramos-Cordoba, M. Via-Nadal, M. Piris and E. Matito, Phys. Chem. Chem. Phys., 2017, 19, 24029–24041 RSC
.
- I. Mitxelena, M. Piris and M. Rodriguez-Mayorga, J. Phys.: Condens.Matter, 2017, 29, 425602 CrossRef CAS
.
- I. Mitxelena, M. Piris and M. Rodriguez-Mayorga, J. Phys.: Condens.Matter, 2018, 30, 089501 CrossRef
.
- E. V. Ludeña, F. J. Torres and C. Costa, J. Mod. Phys., 2013, 04, 391–400 CrossRef
.
- K. Pernal, Comput. Theor. Chem., 2013, 1003, 127–129 CrossRef CAS
.
- M. Piris, J. M. Matxain and X. Lopez, J. Chem. Phys., 2013, 139, 234109 CrossRef CAS
.
- P. O. Löwdin and H. Shull, Phys. Rev., 1956, 101, 1730–1739 CrossRef
.
- M. Piris and J. M. Ugalde, J. Comput. Chem., 2009, 30, 2078–2086 CrossRef CAS PubMed
.
- M. Piris, Int. J. Quantum Chem., 2006, 106, 1093–1104 CrossRef CAS
.
- D. A. Mazziotti, Chem. Phys. Lett., 1998, 289, 419–427 CrossRef CAS
.
- W. Kutzelnigg and D. Mukherjee, J. Chem. Phys., 1999, 110, 2800–2809 CrossRef CAS
.
- P. Leiva and M. Piris, J. Chem. Phys., 2005, 123, 214102–214107 CrossRef CAS PubMed
.
- M. Piris, X. Lopez and J. M. Ugalde, J. Chem. Phys., 2007, 126, 214103–214105 CrossRef CAS PubMed
.
- M. Piris, J. M. Matxain, X. Lopez and J. M. Ugalde, J. Chem. Phys., 2010, 132, 031103 CrossRef CAS PubMed
.
- M. Piris, J. M. Matxain, X. Lopez and J. M. Ugalde, J. Chem. Phys., 2010, 133, 111101 CrossRef CAS
.
- M. Piris, X. Lopez, F. Ruipérez, J. M. Matxain and J. M. Ugalde, J. Chem. Phys., 2011, 134, 164102 CrossRef CAS PubMed
.
- M. Piris, J. Chem. Phys., 2014, 141, 044107 CrossRef CAS PubMed
.
- M. Piris, Phys. Rev. Lett., 2017, 119, 063002–063005 CrossRef PubMed
.
- M. Piris, J. Math. Chem., 1999, 25, 47–54 CrossRef CAS
.
-
I. Mitxelena, M. Piris and J. M. Ugalde, in State Art Mol. Electron. Struct. Comput. Correl. Methods, Basis Sets More, ed. P. Hoggan and U. Ancarani, Academic Press, 2019, ch. 7, vol. 79 of Advances in Quantum Chemistry, pp. 155–177 Search PubMed
.
-
M. Piris, in Quantum Chemistry at the Dawn of the 21st Century. Series: Innovations in Computational Chemistry, ed. R. Carbó-Dorca and T. Chakraborty, Apple Academic Press, 2018, ch. 22, pp. 593–620 Search PubMed
.
- M. Piris, J. Chem. Phys., 2013, 139, 064111 CrossRef CAS PubMed
.
- M. Piris, F. Ruipérez and J. Matxain, Mol. Phys., 2014, 112, 711–718 CrossRef
.
- M. Piris, Phys. Rev. A, 2018, 98, 022504–022506 CrossRef CAS
.
- M. Rodríguez-Mayorga, I. Mitxelena, F. Bruneval and M. Piris, J. Chem. Theory Comput., 2021, 17, 7562–7574 CrossRef PubMed
.
- M. Piris, Phys. Rev. Lett., 2021, 127, 233001 CrossRef CAS PubMed
.
- E. Cancès and K. Pernal, J. Chem. Phys., 2008, 128, 134108 CrossRef
.
- M. Piris and I. Mitxelena, Comput. Phys. Commun., 2021, 259, 107651 CrossRef CAS
.
- J. F. H. Lew-Yee, M. Piris and J. M. del Campo, J. Chem. Phys., 2021, 154, 064102 CrossRef CAS PubMed
.
- I. Mitxelena, M. Rodríguez-Mayorga and M. Piris, Eur. Phys. J. B, 2018, 91, 109 CrossRef
.
- I. Mitxelena and M. Piris, J. Phys.: Condens.Matter, 2020, 32, 17LT01 CrossRef CAS PubMed
.
- I. Mitxelena and M. Piris, J. Chem. Phys., 2020, 152, 064108 CrossRef CAS PubMed
.
- I. Mitxelena and M. Piris, J. Chem. Phys., 2022, 156, 214102 CrossRef CAS PubMed
.
- I. Mitxelena and M. Piris, J. Chem. Phys., 2024, 160, 204106–204108 CrossRef CAS PubMed
.
- X. Lopez, F. Ruipérez, M. Piris, J. M. Matxain and J. M. Ugalde, ChemPhysChem, 2011, 12, 1061–1065 CrossRef CAS PubMed
.
- J. J. M. Matxain, F. Ruipérez, I. Infante, X. Lopez, J. J. M. Ugalde, G. Merino and M. Piris, J. Chem. Phys., 2013, 138, 151102 CrossRef PubMed
.
- M. Piris and N. H. March, J. Phys. Chem. A, 2015, 119, 10190–10194 CrossRef CAS PubMed
.
- J. M. Mercero, R. Grande-Aztatzi, J. M. Ugalde and M. Piris, Adv. Quantum Chem., 2023, 88, 229–248 CrossRef CAS
.
- J. F. H. Lew-Yee and J. M. Campo, AIP Adv., 2023, 13, 065213 CrossRef
.
- X. Lopez, M. Piris, J. M. Matxain and J. M. Ugalde, Phys. Chem.
Chem. Phys., 2010, 12, 12931–12934 RSC
.
- X. Lopez, F. Ruipérez, M. Piris, J. M. Matxain, E. Matito and J. M. Ugalde, J. Chem. Theory Comput., 2012, 8, 2646–2652 CrossRef CAS PubMed
.
- X. Lopez, M. Piris, F. Ruipérez and J. J. M. Ugalde, J. Phys. Chem. A, 2015, 119, 6981–6988 CrossRef CAS PubMed
.
- M. Piris, X. Lopez and J. M. Ugalde, Chem.—Eur. J., 2016, 22, 4109–4115 CrossRef CAS PubMed
.
- X. Lopez and M. Piris, Theor. Chem. Acc., 2019, 138, 89 Search PubMed
.
- J. M. Mercero, J. M. Ugalde and M. Piris, Theor. Chem. Acc., 2021, 140, 74 Search PubMed
.
- J. F. H. Lew-Yee, J. M. del Campo and M. Piris, J. Chem. Theory Comput., 2023, 19, 211–220 CrossRef CAS PubMed
.
- E. Ramos-Cordoba, X. Lopez, M. Piris and E. Matito, J. Chem. Phys., 2015, 143, 164112 CrossRef
.
- J. M. Matxain, M. Piris, F. Ruipérez, X. Lopez and J. M. Ugalde, Phys. Chem. Chem. Phys., 2011, 13, 20129–20135 RSC
.
- F. Ruipérez, M. Piris, J. M. Ugalde and J. M. Matxain, Phys. Chem. Chem. Phys., 2013, 15, 2055–2062 RSC
.
- M. Piris and N. H. March, Phys. Chem. Liq., 2016, 54, 797–801 CrossRef CAS
.
- J. F. H. Lew-Yee, M. Piris and J. M. Campo, J. Chem. Phys., 2023, 158, 084110 CrossRef CAS
.
- Y. Lemke, J. Kussmann and C. Ochsenfeld, J. Chem. Theory Comput., 2022, 18, 4229–4244 CrossRef CAS PubMed
.
- N. G. Cartier and K. J. Giesbertz, J. Chem. Theory Comput., 2024, 20, 3669–3682 CrossRef CAS PubMed
.
- M. Vladaj, Q. Marécat, B. Senjean and M. Saubanère, J. Chem. Phys., 2024, 161, 074105 CrossRef CAS PubMed
.
- L. Franco, I. Bonfil-Rivera, J. F. H. Lew-Yee, M. Piris, J. M. del Campo and R. A. Vargas-Hernandez, J. Chem. Phys., 2024, 160, 244107 CrossRef CAS PubMed
.
- R. Shepard, Adv. Chem. Phys., 1987, 69, 63–200 CrossRef CAS
.
- U. Bozkaya, J. M. Turney, Y. Yamaguchi, H. F. Schaefer and C. D. Sherrill, J. Chem. Phys., 2011, 135, 104103–104117 CrossRef PubMed
.
- I. A. Elayan, R. Gupta and J. W. Hollett, J. Chem. Phys., 2022, 156, 094102 CrossRef CAS PubMed
.
- P. Leiva and M. Piris, Int. J. Quantum Chem., 2007, 107, 1–11 CrossRef CAS
.
- M. Piris, J. M. Matxain, X. Lopez and J. M. Ugalde, J. Chem. Phys., 2009, 131, 021102 CrossRef CAS PubMed
.
- R. Quintero-Monsebaiz, I. Mitxelena, M. Rodríguez-Mayorga, A. Vela and M. Piris, J. Phys.: Condens.Matter, 2019, 31, 165501–165508 CrossRef CAS PubMed
.
- M. Piris, Phys. Rev. A, 2019, 100, 32508 CrossRef CAS
.
- I. Mitxelena and M. Piris, J. Chem. Phys., 2020, 153, 044101 CrossRef CAS PubMed
.
- R. Quintero-Monsebaiz, L. I. Perea-Ramírez, M. Piris and A. Vela, Phys. Chem. Chem. Phys., 2021, 19, 2953–2963 RSC
.
- I. Mitxelena and M. Piris, J. Chem. Phys., 2017, 146, 014102–014107 CrossRef
.
- I. Mitxelena and M. Piris, J. Math. Chem., 2018, 56, 1445–1455 CrossRef CAS
.
- A. Rivero-Santamaría and M. Piris, J. Chem. Phys., 2024, 160, 071102 CrossRef
.
- K. Pernal, K. Giesbertz, O. V. Gritsenko and E. J. Baerends, J. Chem. Phys., 2007, 127, 214101 CrossRef PubMed
.
- K. Giesbertz, E. Baerends and O. V. Gritsenko, Phys. Rev. Lett., 2008, 101, 033004 CrossRef CAS PubMed
.
- R. van Meer, O. V. Gritsenko and E. J. Baerends, J. Chem. Phys., 2017, 146, 044119 CrossRef CAS
.
- C. Schilling and S. Pittalis, Phys. Rev. Lett., 2021, 127, 023001 CrossRef CAS PubMed
.
- J. Liebert, F. Castillo, J.-P. Labbé and C. Schilling, J. Chem. Theory Comput., 2022, 18, 124–140 CrossRef CAS PubMed
.
- D. W. Smith and O. W. Day, J. Chem. Phys., 1975, 62, 113–114 CrossRef CAS
.
- O. W. Day, D. W. Smith and R. C. Morrison, J. Chem. Phys., 1975, 62, 115–119 CrossRef CAS
.
- D. J. Rowe, Rev. Mod. Phys., 1968, 40, 153–166 CrossRef
.
- K. Pernal and J. Cioslowski, Chem. Phys. Lett., 2005, 412, 71–75 CrossRef CAS
.
- P. Leiva and M. Piris, J. Mol. Struct.: THEOCHEM, 2006, 770, 45–49 CrossRef CAS
.
- M. Piris, J. M. Matxain, X. Lopez and J. M. Ugalde, J. Chem. Phys., 2012, 136, 174116 CrossRef PubMed
.
- E. N. Zarkadoula, S. Sharma, J. K. Dewhurst, E. K. U. Gross and N. N. Lathiotakis, Phys. Rev. A, 2012, 85, 032504 CrossRef
.
- S. Di Sabatino, J. Koskelo, J. A. Berger and P. Romaniello, Phys. Rev. B, 2022, 105, 235123 CrossRef CAS
.
- S. Di Sabatino, J. Koskelo, J. A. Berger and P. Romaniello, Phys. Rev. B, 2023, 107, 035111 CrossRef CAS
.
- K. Chatterjee and K. Pernal, J. Chem. Phys., 2012, 137, 204109 CrossRef PubMed
.
- J. F. H. Lew-Yee, I. A. Bonfil-Rivera, M. Piris and J. M. del Campo, J. Chem. Theory Comput., 2024, 20, 2140–2151 CrossRef PubMed
.
- M. Piris and P. Otto, Int. J. Quantum Chem., 2005, 102, 90–97 CrossRef CAS
.
- S. Sharma, J. K. Dewhurst, S. Shallcross and E. K. U. Gross, Phys. Rev. Lett., 2013, 110, 116403–116405 CrossRef CAS PubMed
.
- Y. Shinohara, S. Sharma, S. Shallcross, N. N. Lathiotakis and E. K. U. Gross, J. Chem. Theory Comput., 2015, 11, 4895–4899 CrossRef CAS PubMed
.
- M. Saubanère and G. M. Pastor, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 035111 CrossRef
.
- J. Schmidt, C. L. Benavides-Riveros and M. A. L. Marques, Phys. Rev. B, 2019, 99, 224502 CrossRef CAS
.
- L. M. Mentel, X. W. Sheng, O. V. Gritsenko and E. J. Baerends, J. Chem. Phys., 2012, 137, 204117 CrossRef CAS PubMed
.
- X. Shao, L. Paetow, M. E. Tuckerman and M. Pavanello, Nat. Commun., 2023, 14, 6281 CrossRef CAS PubMed
.
- B. Kalita, L. Li, R. J. McCarty and K. Burke, Acc. Chem. Res., 2021, 54, 818–826 CrossRef CAS
.
- J. T. Margraf and K. Reuter, Nat. Commun., 2021, 12, 344 CrossRef CAS PubMed
.
- J. Schmidt, M. Fadel and C. L. Benavides-Riveros, Phys. Rev. Res., 2021, 3, L032063 CrossRef CAS
.
- R. Hoffmann and J. P. Malrieu, Angew. Chem., Int. Ed., 2020, 59, 12590–12610 CrossRef CAS PubMed
.
- S. E. Smart and D. A. Mazziotti, Phys. Rev. Lett., 2021, 126, 070504 CrossRef CAS PubMed
.
- S. E. Smart and D. A. Mazziotti, Phys. Rev. A, 2022, 105, 1–11 Search PubMed
.
- M. Rodríguez-Mayorga, K. J. H. Giesbertz and L. Visscher, SciPost Chemistry, 2022, 1, 004 CrossRef
.
- J. F. H. Lew-Yee, J. M. del Campo and M. Piris, 2024, 1–10, in preparation.
| This journal is © The Royal Society of Chemistry 2024 |
