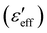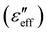Effect of rotational shear on the dielectric dispersion of a nematic liquid crystal above the Freedericksz threshold field†
K. Anaswara
Das
a,
M. Praveen
Kumar
a,
Simon
Čopar
 bc and
Surajit
Dhara
bc and
Surajit
Dhara
 *a
*a
aSchool of Physics, University of Hyderabad, Hyderabad-500046, India. E-mail: surajit@uohyd.ac.in
bJ. Stefan Institute, Jamova 39, SI-1000 Ljubljana, Slovenia
cFaculty of Mathematics and Physics, University of Ljubljana, Jadranska 19, SI-1000 Ljubljana, Slovenia
First published on 14th August 2024
Abstract
Rheo-dielectric studies of soft materials provide important information on the dynamic structure and electric polarization. We study the dielectric dispersion of a nematic liquid crystal by applying a high AC probe field without a DC bias and a low AC probe field with a high DC bias under steady rotational shear. The dielectric anisotropy of the nematic is positive and the applied electric field is parallel to the velocity gradient with a magnitude larger than the Freedericksz threshold field. We find that the dielectric dispersion and the relaxation frequencies are strongly shear rate dependent. The analysis of the results based on a simple physical model shows that the effective dielectric constant of the nematic with non-uniform director tilt in the shear plane can be modelled as a series combination of parallel and perpendicular components. Our experiments demonstrate changes in dielectric dispersion are due to molecular reorientation under the influence of the competing effects of hydrodynamic and dielectric torques.
1 Introduction
The structures and properties of complex fluids such as polymeric systems, colloidal suspensions and liquid crystals have been studied under simultaneous shear flow and electric fields.1,2 In some fluids, the viscosity is enhanced significantly due to the application of an electric field. This effect is known as the electrorheological effect and is very important for applications in electromechanical devices.3–6 In nematic liquid crystals (LCs), composed of axially polar molecules, under the application of sufficient electric field the effective viscosity is enhanced and this effect is due to the change in the orientation of the director (average aligning direction of the molecules) with respect to the shear flow direction.7–14 In uniaxial nematic LCs, there are two principal dielectric constants, namely ε‖ and ε⊥, where the subscripts refer to components in relation to the director.15 The dielectric anisotropy (Δε = ε‖ − ε⊥) of the nematic LCs composed of polar molecules could be zero, positive or negative, depending on the orientation of the permanent dipole moments with respect to the long molecular axis.Both the dielectric constants are frequency dependent and the corresponding relaxation frequencies f‖ and f⊥ are related to the time scales of rotation of the off-axis dipoles along the short and long molecular axes, respectively.16 For axially polar molecules, the relaxation frequency f‖ is much smaller than f⊥ and it is the opposite in the case of transversely polar molecules.16 Usually, these relaxation frequencies are measured in cells composed of parallel electrodes in which the director is aligned either perpendicular (homeotropic) or parallel (homogeneous) to the electrodes. In cells the nematic LCs are in the quiescent state, hence such measurements provide equilibrium relaxation times which are important for device applications.
A nematic LC is far away from the equilibrium when subjected to a steady shear flow and depending on the system it may exhibit three dynamic modes, namely flow-aligned, wagging and tumbling.17–22 In flow-aligned nematics, the director forms a steady state with a tilt angle θL (Leslie angle) with respect to the flow direction whereas, in the case of wagging, the director oscillates and for tumbling motions, the director makes full rotations in the shear plane.23–27 In a flow-aligned nematic with positive dielectric anisotropy (Δε > 0) the application of a sufficiently high electric field perpendicular to the flow direction induces an apparent change in viscosity.13,14,28 The change in viscosity due to the change in the director orientation can be measured easily from the rheo-dielectric studies at a frequency much below the dielectric relaxation frequency.11,13,14,29,30 The effect of shear flow on the dielectric dispersion of the nematic LCs measured at the non-aligning electric field (low voltage) has been studied.31,32 Since the shear rate is much slower than the equilibrium rotation of the dipoles (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a2.gif) ≪ τ−1, relaxation time), the shear flow does not affect the dielectric relaxation frequency directly.31 However, the effect of shear on the dielectric dispersion above the Freedericksz threshold field is unexplored and hence requires comprehensive studies.
≪ τ−1, relaxation time), the shear flow does not affect the dielectric relaxation frequency directly.31 However, the effect of shear on the dielectric dispersion above the Freedericksz threshold field is unexplored and hence requires comprehensive studies.
In this paper, we apply a sufficiently high electric field that tends to orient the nematic director along the velocity gradient (perpendicular to the shear flow direction) and study the frequency dispersion of the effective dielectric constant at various shear rates. We measured the real and imaginary parts of the dielectric constant at high AC as well as low AC with high DC bias fields and analysed their frequency dependence at different shear rates. Our study shows that the DC bias field merely aligns the director whereas the high probe AC field induces a non-linear dielectric response. We observed a decrease in both real and imaginary dielectric constants as well as the viscosity with increasing shear rates, consistent with the proposed director field.
2 Experiment
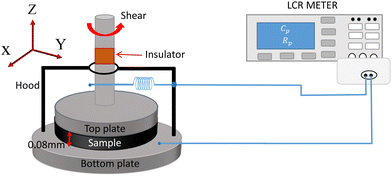
We worked on a nematic liquid crystal mixture, known as E7. It is a mixture of several cyanobiphenyl, cyanoterphenol and triphenyl compounds at some specific compositions.33 It was obtained from Grandinchem, and used without further purification. At 5 °C, the parallel and perpendicular components of the dielectric constant are given by ε‖ = 19.6 and ε⊥ = 4.5, respectively, and the dielectric anisotropy is positive (Δε = ε‖ − ε⊥ = 15.1) (Fig. S1, ESI†)34. The nematic to isotropic phase transition temperature is 61 °C and it exhibits a broad nematic temperature range (61 °C to −10 °C). The rheo-dielectric measurements were made with the help of a rheometer (Anton Paar MCR 501) using parallel-plate geometry with a plate diameter of 50 mm. The plate gap was fixed at 80 μm and no alignment layer was used in this experiment. The bottom plate was fixed while the top plate was rotated at different shear rates. The bottom plate is equipped with a Peltier temperature controller for controlling the temperature. A hood was used to cover the measuring plates for temperature uniformity. An LCR meter (Agilent E4980A) was connected to the plates for rheo-dielectric measurements. The frequency was varied from 100 Hz to 1.0 MHz in all experiments. The experiments were performed at different shear rates and the frequency-dependent real and imaginary parts of the dielectric constant were measured by the LCR meter. All the measurements were made at 5 °C. Before the measurement, the sample was pre-sheared for 5 minutes at a fixed shear rate (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a2.gif) =100 s−1) to remove heterogeneity in the deformation in the quiescent state. A schematic diagram of the experimental setup is shown in Fig. 1.
=100 s−1) to remove heterogeneity in the deformation in the quiescent state. A schematic diagram of the experimental setup is shown in Fig. 1.
3 Results and discussion
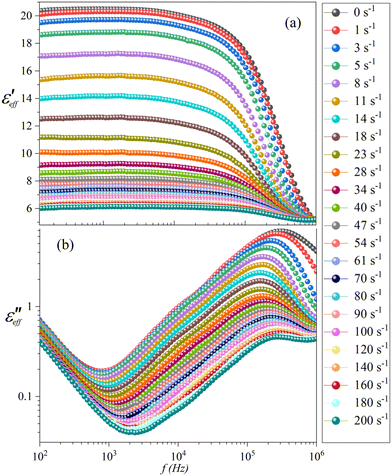
We measured the frequency dispersion of the effective dielectric constants at a fixed electric field and different shear rates. At room temperature the complete relaxation mode is not observed due to the limiting frequency range of the LCR meter (2 MHz) hence, all the experiments were performed at a fixed temperature of 5 °C. Fig. 2(a) and (b) shows the dielectric dispersion of the real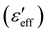 and imaginary
and imaginary 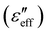 parts of the effective dielectric constant at different shear rates. The applied voltage was 20 V AC, which is nearly 20 times larger than the Freedericksz threshold voltage (Vth = 0.9 V). In the low-frequency region (f < 104 Hz), at zero shear rate (i.e., quiescent nematic),
parts of the effective dielectric constant at different shear rates. The applied voltage was 20 V AC, which is nearly 20 times larger than the Freedericksz threshold voltage (Vth = 0.9 V). In the low-frequency region (f < 104 Hz), at zero shear rate (i.e., quiescent nematic), 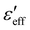 is independent of frequency and decreases with increasing shear rate. On the other hand,
is independent of frequency and decreases with increasing shear rate. On the other hand, 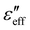 decreases with the increasing frequency in the low-frequency region (f < 103 Hz). It varies as
decreases with the increasing frequency in the low-frequency region (f < 103 Hz). It varies as 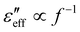 , which suggests the influence of the conductivity (direct current) on the imaginary component of the dielectric constant.
, which suggests the influence of the conductivity (direct current) on the imaginary component of the dielectric constant.
Fig. 3(a) shows the variation of 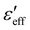 obtained from Fig. 2 with the shear rate at a fixed frequency f = 4 kHz. It decreases exponentially with increasing shear rate. For example, at
obtained from Fig. 2 with the shear rate at a fixed frequency f = 4 kHz. It decreases exponentially with increasing shear rate. For example, at ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a2.gif) = 0 s−1,
= 0 s−1, 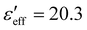 . This value is nearly equal to the parallel component of the dielectric constant measured in a homeotropic cell i.e., ε‖ ≃ 19.6 (Fig. S1(b), ESI†).34 It suggests that the director is almost perpendicular to the confining plates and parallel to the direction of the electric field. With increasing shear rate,
. This value is nearly equal to the parallel component of the dielectric constant measured in a homeotropic cell i.e., ε‖ ≃ 19.6 (Fig. S1(b), ESI†).34 It suggests that the director is almost perpendicular to the confining plates and parallel to the direction of the electric field. With increasing shear rate, 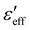 decreases rapidly and eventually becomes constant i.e,
decreases rapidly and eventually becomes constant i.e, 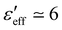 , when the shear rate is increased to
, when the shear rate is increased to ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a2.gif) = 200 s−1. This dielectric constant is slightly larger than the value measured in a homogeneous (planar) cell i.e., εp ≃ 4.5 (Fig. S1(a), ESI†).34 Hence, these results demonstrate that initially (
= 200 s−1. This dielectric constant is slightly larger than the value measured in a homogeneous (planar) cell i.e., εp ≃ 4.5 (Fig. S1(a), ESI†).34 Hence, these results demonstrate that initially (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a2.gif) = 0 s−1) the director is perpendicular to the plates i.e., parallel to the velocity gradient direction and it gradually tilts in the shear plane towards the shear flow direction. Further, the effective viscosity ηeff of the liquid crystal was measured simultaneously with the dielectric dispersion measurements. Fig. 2(b) shows that the viscosity is independent of time but decreases with increasing shear rate. Fig. 2(c) shows the shear rate-dependent viscosity of the sample. At
= 0 s−1) the director is perpendicular to the plates i.e., parallel to the velocity gradient direction and it gradually tilts in the shear plane towards the shear flow direction. Further, the effective viscosity ηeff of the liquid crystal was measured simultaneously with the dielectric dispersion measurements. Fig. 2(b) shows that the viscosity is independent of time but decreases with increasing shear rate. Fig. 2(c) shows the shear rate-dependent viscosity of the sample. At ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a2.gif) = 1 s−1, ηeff = 0.7 Pa s and it reduces to about 0.1 Pa s when
= 1 s−1, ηeff = 0.7 Pa s and it reduces to about 0.1 Pa s when ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a2.gif) = 200 s−1. The effective viscosity at
= 200 s−1. The effective viscosity at ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a2.gif) = 1 s−1 can be considered as the Miesowicz viscosity for the director orientation being parallel to the velocity gradient direction i.e., ηeff ≃ η1 and at the highest shear rate (
= 1 s−1 can be considered as the Miesowicz viscosity for the director orientation being parallel to the velocity gradient direction i.e., ηeff ≃ η1 and at the highest shear rate (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a2.gif) = 200 s−1), ηeff ≃ η2, where η2 is the Miesowicz viscosity with the director being nearly parallel to the velocity direction. It may also be noted that the frequency at which the peak occurs in
= 200 s−1), ηeff ≃ η2, where η2 is the Miesowicz viscosity with the director being nearly parallel to the velocity direction. It may also be noted that the frequency at which the peak occurs in 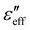 , so-called dielectric relaxation frequency also changes with the shear rate (Fig. 2(b)). To obtain the actual dielectric relaxation frequency (fr), we fitted the dielectric data to the Havriliak–Negami (HN) relaxation function (Fig. S2, ESI†)34
, so-called dielectric relaxation frequency also changes with the shear rate (Fig. 2(b)). To obtain the actual dielectric relaxation frequency (fr), we fitted the dielectric data to the Havriliak–Negami (HN) relaxation function (Fig. S2, ESI†)34
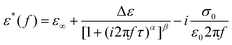 | (1) |
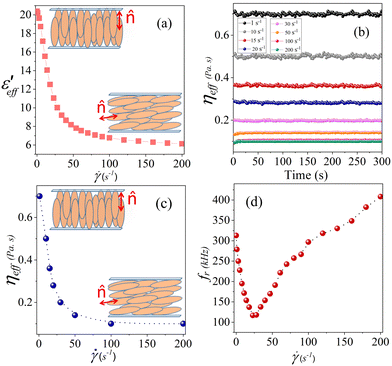 | ||
Fig. 3 Variation of (a)  with shear rate at frequency f = 4 kHz (obtained from Fig. 2). (b) Time-dependent effective viscosity ηeff measured at 20 V AC at temperature 5 °C. (c) Variation of ηeff at different shear rates obtained from the figure (b). Shear-dependent director orientations are shown in the insets. (d) Variation of the relaxation frequency fr with shear rate, obtained from the fitting of Havriliak–Negami equation. with shear rate at frequency f = 4 kHz (obtained from Fig. 2). (b) Time-dependent effective viscosity ηeff measured at 20 V AC at temperature 5 °C. (c) Variation of ηeff at different shear rates obtained from the figure (b). Shear-dependent director orientations are shown in the insets. (d) Variation of the relaxation frequency fr with shear rate, obtained from the fitting of Havriliak–Negami equation. | ||
where Δε is the dielectric strength, ε∞ is the dielectric permittivity at the high-frequency limit, σ0 is the conductivity and τ is the relaxation time.35 The corresponding relaxation frequency is given by fr = 1/2πτ. The exponents α and β describe the asymmetry and broadness of the corresponding spectra, and appear independent from the shear rate. The data shows α ≈ 0.9 and β ≈ 1 (Table S1, ESI†)34 and suggests that the shear rate does not fundamentally affect the material's structure and order. Fig. 3(d) shows the variation of the obtained relaxation frequency fr with the shear rate. The relaxation frequency decreases from 320 kHz to 116.7 kHz when ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a2.gif) is increased from 0 to 23 s−1. It shows a minimum at
is increased from 0 to 23 s−1. It shows a minimum at ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a2.gif) = 23 s−1, and then increases to about 400 kHz, when
= 23 s−1, and then increases to about 400 kHz, when ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a2.gif) is further increased to 200 s−1. At
is further increased to 200 s−1. At ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a2.gif) = 0 s−1, the director is parallel to the field direction, hence the effective relaxation frequency fr corresponds to the rotation of the longitudinal (axial) components of the dipole moments about the short axis i.e., fr = 320 kHz ∼ f‖r, where f‖r is the relaxation frequency measured in homeotropic cell (quiescent nematic) (Fig. S1(b), ESI†).34 The relaxation frequency (f⊥r) of the transverse dipole moments about the long axis in the homogeneous cell (quiescent nematic) is greater than 2 MHz (Fig. S1(a), ESI†),34 which is much larger than f‖r. We performed experiments at another lower voltage (15 V) and observed similar dielectric dispersion (Fig. S3 and S4, ESI†).34 The change in the relaxation frequency under shear is quite unexpected and requires further investigation (see later discussion). Here, two possible director dynamics should be mentioned. Any effect of electrohydrodynamic instability (EHD) on the dielectric relaxation is ruled out as both the dielectric and conductivity anisotropies (Δε and Δσ) are positive.36 Moreover, our experimental frequency range is higher than those used in low-frequency EHD studies.37–39 Further, E7 is a flow-aligning nematic hence the tumbling and wagging of the director is absent.40
= 0 s−1, the director is parallel to the field direction, hence the effective relaxation frequency fr corresponds to the rotation of the longitudinal (axial) components of the dipole moments about the short axis i.e., fr = 320 kHz ∼ f‖r, where f‖r is the relaxation frequency measured in homeotropic cell (quiescent nematic) (Fig. S1(b), ESI†).34 The relaxation frequency (f⊥r) of the transverse dipole moments about the long axis in the homogeneous cell (quiescent nematic) is greater than 2 MHz (Fig. S1(a), ESI†),34 which is much larger than f‖r. We performed experiments at another lower voltage (15 V) and observed similar dielectric dispersion (Fig. S3 and S4, ESI†).34 The change in the relaxation frequency under shear is quite unexpected and requires further investigation (see later discussion). Here, two possible director dynamics should be mentioned. Any effect of electrohydrodynamic instability (EHD) on the dielectric relaxation is ruled out as both the dielectric and conductivity anisotropies (Δε and Δσ) are positive.36 Moreover, our experimental frequency range is higher than those used in low-frequency EHD studies.37–39 Further, E7 is a flow-aligning nematic hence the tumbling and wagging of the director is absent.40
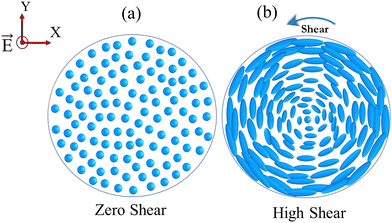
We propose possible director configurations at zero and high shear rates based on the above results and discussion. In our experiment, the bottom plate is fixed and the top plate is rotated with different shear rates. At zero shear rate, the molecules are aligned perpendicular to the plates as the applied voltage is very much greater than the Freedericksz threshold voltage as shown in Fig. 4(a). At a higher shear rate, the hydrodynamic torque due to the shear flow is much larger than the dielectric torque due to the applied voltage. As a result, the molecules tend to align parallel to the shear flow direction. Further, the shear rate experienced by fluid elements in parallel plate geometry depends on their position r (distance from the centre of plates) and is given by ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a2.gif) = rω/h, where h is the gap between the plates and ω is the angular frequency. Conventionally, in parallel plate systems, the shear rate at the rim (r = a) is considered for the calculation of stress and viscosity, where a is the radius of the plate. In parallel plate geometry, the shear rate, and consequently the hydrodynamic torque depends on r and is not the same throughout the plate. It is zero at the centre and increases from the centre to the edge of the plates. As a result, the director at the centre is vertical and, as one moves towards the perimeter, the director tilts continuously towards the shear flow direction, creating a half skyrmion-like director deformation as shown in Fig. 4(b). Such a complex director distortion can give rise to a nonuniform director structure and the applied field encounters a spatially varied dielectric constant. The proposed director structure can be confirmed by rheo-microscopy or rheo-X-rays experiments using transparent electrodes.
= rω/h, where h is the gap between the plates and ω is the angular frequency. Conventionally, in parallel plate systems, the shear rate at the rim (r = a) is considered for the calculation of stress and viscosity, where a is the radius of the plate. In parallel plate geometry, the shear rate, and consequently the hydrodynamic torque depends on r and is not the same throughout the plate. It is zero at the centre and increases from the centre to the edge of the plates. As a result, the director at the centre is vertical and, as one moves towards the perimeter, the director tilts continuously towards the shear flow direction, creating a half skyrmion-like director deformation as shown in Fig. 4(b). Such a complex director distortion can give rise to a nonuniform director structure and the applied field encounters a spatially varied dielectric constant. The proposed director structure can be confirmed by rheo-microscopy or rheo-X-rays experiments using transparent electrodes.
Dielectric spectroscopic experiments are usually done with a relatively small probe field to ensure a linear regime.41 To avoid nonlinear response, we performed dielectric dispersion measurements under a high DC bias voltage (20 V) with a small AC probe voltage (0.7 V). The results are shown in Fig. 5(a) and (b). Both the dispersion curves apparently look very similar to Fig. 2(a) and (b). For example, 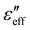 decreases similar way with increasing shear rate as observed in Fig. 3(a). The variation of the dielectric relaxation frequency with the shear rate obtained from the fitting (Fig. S6, ESI†)34 with eqn (1) is shown in Fig. 5(d). The relaxation frequency is found to increase beyond shear rate 5 s−1 as opposed to the measurements made at a high AC electric field (Fig. 3(d)). The enhancement of the relaxation frequency in this condition is expected because the director tilts with increasing shear rates. The director distortion under fields can give rise to flexoelectric polarisation15,36 which can couple to the orientational fluctuations of the director. As a result, it can give rise to a collective polarisation mode. However, such polarization is expected to relax at a much lower frequency42 hence the influence of flexoelectric polarization can be ignored in our experiments. It suggests that the non-monotonous variation of the relaxation frequency under the high AC field is not due to any collective relaxation processes. Hence, the overall results hint toward nonlinear dielectric effects arising due to the high probe field and shear flow. In fact very recent studies reported that even small electric fields in an unaligned nematic liquid crystal can lead to a nonlinear dielectric response.41
decreases similar way with increasing shear rate as observed in Fig. 3(a). The variation of the dielectric relaxation frequency with the shear rate obtained from the fitting (Fig. S6, ESI†)34 with eqn (1) is shown in Fig. 5(d). The relaxation frequency is found to increase beyond shear rate 5 s−1 as opposed to the measurements made at a high AC electric field (Fig. 3(d)). The enhancement of the relaxation frequency in this condition is expected because the director tilts with increasing shear rates. The director distortion under fields can give rise to flexoelectric polarisation15,36 which can couple to the orientational fluctuations of the director. As a result, it can give rise to a collective polarisation mode. However, such polarization is expected to relax at a much lower frequency42 hence the influence of flexoelectric polarization can be ignored in our experiments. It suggests that the non-monotonous variation of the relaxation frequency under the high AC field is not due to any collective relaxation processes. Hence, the overall results hint toward nonlinear dielectric effects arising due to the high probe field and shear flow. In fact very recent studies reported that even small electric fields in an unaligned nematic liquid crystal can lead to a nonlinear dielectric response.41
 | ||
Fig. 5 (a) and (b) Dielectric dispersions were measured using 0.7 V AC probe voltage with 20 V DC bias. Continuous lines are the least square fits of the data to eqn (2). Variation of effective (c) dielectric constant 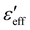 and (d) relaxation frequency with shear rate and (d) relaxation frequency with shear rate ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a2.gif) . Inset shows the dependence of the director tilt angle θ on the shear rate. Dotted lines are a guide to the eye. Measurements are done at temperature T = 5 °C. Due to insufficient data in the high-frequency range, the relaxation frequency beyond 54 s−1 can not be obtained from the HN fitting. . Inset shows the dependence of the director tilt angle θ on the shear rate. Dotted lines are a guide to the eye. Measurements are done at temperature T = 5 °C. Due to insufficient data in the high-frequency range, the relaxation frequency beyond 54 s−1 can not be obtained from the HN fitting. | ||
We attempt to reconstruct the measurements as different combinations of the same elementary dielectric responses. In the simplest terms, we consider the LC under shear alignment as having a constant angle with respect to the external electric field. Such a material has an effective dielectric response
εeff = ε‖cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ + ε⊥sin2 θ + ε⊥sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ | (2) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a2.gif) ) are determined by least squares fitting. Note that θ(
) are determined by least squares fitting. Note that θ(![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a2.gif) ) in the inset assumes the highest shear rate corresponds to θ = 90°, as there is no way of determining the average director tilt from the dielectric measurements alone. For this reason, the fit shows that the model is capable of reproducing the measurements, and thus no other major effects were missed, but cannot confidently rely on the component dielectric responses obtained from the model.
) in the inset assumes the highest shear rate corresponds to θ = 90°, as there is no way of determining the average director tilt from the dielectric measurements alone. For this reason, the fit shows that the model is capable of reproducing the measurements, and thus no other major effects were missed, but cannot confidently rely on the component dielectric responses obtained from the model.
Further, a few comments are in order. First, two dimensionless numbers, that characterize the flow are Deborah number De = τ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a2.gif) , and Ericksen numbers
, and Ericksen numbers 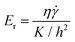 ,43 where τ is the characteristic relaxation time of the material, h is the gap between the two plates, η is the effective viscosity and K is the mean elastic constant. In the experimental shear rate range (
,43 where τ is the characteristic relaxation time of the material, h is the gap between the two plates, η is the effective viscosity and K is the mean elastic constant. In the experimental shear rate range (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/char_e0a2.gif) =1–200 s−1), Er = 102–104 and De = 10−2 ∼ 2 (Table S2, ESI†).34 It suggests a liquid-like response and the viscous effects dominate over the elastic effects. Second, liquid crystals contain finite impurity ions which can move towards the opposite electrodes under ac electric field and create space charge polarization. The electrode charging time τ = λDL/2D, where λD is the Debye screening length, L is the gap between the electrodes and D is the diffusion constant of the ions. Taking D ∼ 10−11 m2 s−1,44λD ∼ 0.1 μm,45L = 80 μm, the estimated electrode polarisation frequency is about 2.5 Hz which is far below the frequency range of our studies. The effective dielectric constants and viscosities obtained at the asymptotic limits of the shear rates and electric field could be used to estimate their anisotropies. The feeble bump observed around 10 kHz in Fig. 2(b) could be related to the nonlinear response as discussed and required further investigation.
=1–200 s−1), Er = 102–104 and De = 10−2 ∼ 2 (Table S2, ESI†).34 It suggests a liquid-like response and the viscous effects dominate over the elastic effects. Second, liquid crystals contain finite impurity ions which can move towards the opposite electrodes under ac electric field and create space charge polarization. The electrode charging time τ = λDL/2D, where λD is the Debye screening length, L is the gap between the electrodes and D is the diffusion constant of the ions. Taking D ∼ 10−11 m2 s−1,44λD ∼ 0.1 μm,45L = 80 μm, the estimated electrode polarisation frequency is about 2.5 Hz which is far below the frequency range of our studies. The effective dielectric constants and viscosities obtained at the asymptotic limits of the shear rates and electric field could be used to estimate their anisotropies. The feeble bump observed around 10 kHz in Fig. 2(b) could be related to the nonlinear response as discussed and required further investigation.
4 Conclusion
We measured the dielectric dispersion of E7 nematic liquid crystal using a high AC probe field without any DC bias and compared the results with the measurements made at a low AC probe field with a high DC bias. In the first case, the AC electric field tends to align the director as well as probe the dielectric properties. In the latter case, the DC bias field acts as an aligning field and the small AC probe field measures the dielectric properties. The relaxation frequency measured at a high AC probe field shows a non-monotonous shear rate dependence, first decreasing but beyond a critical shear rate increasing. On the other hand, the relaxation frequency in the case of low probe field and high DC bias increases with increasing shear rate. The analysis suggests that the dielectric response under a low probe field is linear whereas under a high AC probe field, the dielectric response becomes nonlinear. The effective dielectric constant in both cases decreases significantly under rotational shear due to the tilting of the director in the shear plane. Considering the competing effects of the hydrodynamic and dielectric torques, we proposed possible director configurations at zero and high shear rates. Our analysis based on a simple model shows that the effective dielectric constant under shear can be modelled as a series combination of parallel and perpendicular components. In essence, our findings demonstrate the ability to reproducibly change the dielectric relaxation under the presence of transverse electric and flow fields. These results may be useful for applications of liquid crystals as well as polar liquids in electromechanical devices. We focussed on an apolar nematic LC, however rheo-dielectric studies on liquid crystals with macroscopic polarisations such as ferroelectric nematic and ferroelectric smectics LCs are promising for new relaxation dynamics.Data availability
The authors confirm that the data supporting the findings of this study are available within the article [and/or] its ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. D. acknowledges financial support from SERB (SPR/2022/000001) and the support from the IoE (UoH/IoE/RC1-20-010). A. D. acknowledges DST for fellowship (DST/WISE-PhD/PM/2023/57). We thank Dr Arun Roy for the useful discussions. MPK acknowledges NPDF fellowship of SERB (PDF/2023/003722). We thank one of the referees for providing very useful suggestions regarding the DC bias field experiments.References
- R. G. Larson, The structure and rheology of complex fluids, Oxford University Press, 1999 Search PubMed.
- M. Parthasarathy and D. J. Klingenberg, Mater. Sci. Eng., R, 1996, RI7, 57–103 CrossRef.
- W. W. Winslow, Appl. Phys., 1967, 20, 1137 Search PubMed.
- D. R. Gamota and F. E. Filisko, J. Rheol., 1991, 35, 399–425 CrossRef CAS.
- S. Fukayama and K. Negita, J. Mol. Liq., 2001, 90, 131 CrossRef CAS.
- D. J. Klingenberg, F. V. Swol and C. F. Zukoski, J. Chem. Phys., 1989, 91, 7888–7895 CrossRef CAS.
- T. Carlsson and K. Skarp, Mol. Cryst. Liq. Cryst., 1981, 78, 157 CrossRef CAS.
- S. Skarp, T. Carlsson, S. T. Lagerwall and B. Stebler, Mol. Cryst. Liq. Cryst., 1981, 66, 199 CrossRef.
- K.-L. Tse and A. D. Shine, J. Rheol., 1995, 39, 1021 CrossRef CAS.
- I. Yang and A. D. Shine, J. Rheol., 1992, 36, 1079 CrossRef CAS.
- K. Negita, J. Chem. Phys., 1996, 105, 7837–7841 CrossRef CAS.
- H. Watanabe, T. Inoue and K. Osaki, Rheol. Acta, 1998, 5, 24–25 CAS.
- P. Patrico, C. R. Leal, L. F. V. Pinto, A. Boto and M. T. Cidade, Liq. Cryst., 1999, 39, 25 CrossRef.
- M. T. Cidade, G. Pereira, A. Bubnov, V. Hamplova, M. Kaspar and J. P. Casquilho, Liq. Cryst., 2012, 39, 191 CrossRef CAS.
- P. G. de Gennes, The Physics of liquid crystals, Oxford University Press, 1974 Search PubMed.
- W. H. de Jeu, Physical properties of liquid crystals, Cambridge University Press, 1992 Search PubMed.
- F. M. Leslie, J. Phys. D: Appl. Phys., 1976, 9, 925 CrossRef.
- F. M. Leslie, Adv. Liq. Cryst., 1979, 4, 1 CAS.
- F. M. Leslie, Theory and Applications of Liquid Crystals, 1987, pp. 235–254 Search PubMed.
- Andreas M. Menzel, Phys. Rep., 2015, 554, 1 CrossRef CAS.
- G. Rienäcker and S. Hess, Physica A, 1999, 267, 321 CrossRef.
- V. V. Belyaev, Viscosity of nematic liquid crystals, Cambridge International Science, 1st edn, 2011 Search PubMed.
- A. Archer and R. G. Larson, J. Chem. Phys., 1995, 103, 3108 CrossRef.
- D. J. Ternet, R. G. Larson and L. G. Leal, Rheol. Acta, 1999, 38, 183 CrossRef CAS.
- W. R. Burghardt and G. G. Fuller, Macromolecules, 1991, 24, 2546 CrossRef CAS.
- G. Rienäcker and S. Hess, Physica A, 2002, 315, 537 CrossRef.
- Y. G. Tao, W. K. den Otter and W. J. Briels, Eur. Lett., 2009, 86, 56005 CrossRef.
- N. J. Mottram and G. McKay, C. V. Brown, C. T. Russell, I. C. Sage, and C. Tsakonas, Phys. Rev. E, 2016, 93, 030701(R) Search PubMed.
- J. Ananthaiah, R. Sahoo, M. V. Rasna and S. Dhara, Phy. Rev. E, 2014, 89, 022510 CrossRef CAS.
- J. Ananthaiah, M. Rajeswari, V. S. S. Sastry, R. Dabrowski and S. Dhara, Eur. Phys. J. E, 2011, 34, 74 CrossRef CAS PubMed.
- H. Watanabe, T. Sato, M. Hirose, K. Osaki and M. L. Yao, Rheol. Acta, 1998, 37, 519 CrossRef CAS.
- H. Watanabe, T. Sato, M. Matsumiya, T. Inoue, K. Osaki and N. R. Gakkaishi, J. Soc. Rheol., Jpn., 1999, 27, 121–125 CrossRef CAS.
- https://shop.synthon-chemicals.com/en/LIQUID-CRYSTALS/LIQUID-CRYSTALS-MIXTURES/Liquid-crystal-mixture-E7.html .
- Supplementary material presents additional results of dielectric relaxation at different electric fields, also measurements in homogeneous and homeotropic cells†.
- S. Havriliak and S. Negami, J. Polym., 1967, 8, 161 CrossRef CAS.
- L. M. Blinov and V. G. Chigrinov, Electrooptic Effects in Liquid Crystal Materials, 1994 Search PubMed.
- L. E. Aguirre, E. Anoardo, N. Éber and A. Buka, Phys. Rev. E, 2012, 85, 041703 CrossRef PubMed.
- P. Kumar, J. Heuer, T. T. Katona, N. Éber and A. Buka, Phys. Rev. E, 2010, 81, 020702(R) CrossRef.
- E. I. Rjumtsev and S. G. Polushin, Liq. Cryst., 1993, 13, 623 CrossRef CAS.
- D. J. Ternet, R. G. Larson and L. G. Leal, Rheol. Acta, 1999, 38, 183 CrossRef CAS.
- E. Thoms, L. Yu and R. Richert, J. Mol. Liq., 2022, 368, 120664 CrossRef CAS.
- B. I. Outram and S. J. Elston, Phys. Rev. E, 2013, 88, 012506 CrossRef CAS PubMed.
- R. G. Larson and D. W. Mead, Liq. Cryst., 1993, 15, 151 CrossRef CAS.
- S. Hernàndez-Navarro, P. Tierno, J. Ignés-Mullol and F. Sagués, Soft Matter, 2013, 9, 7999 RSC.
- O. D. Lavrentovich and Curr Opin, Colloid Interface Sci., 2016, 21, 97 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00682h |
| This journal is © The Royal Society of Chemistry 2024 |