Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Reactivities of tertiary phosphines towards allenic, acetylenic, and vinylic Michael acceptors†
Feng
An‡
 a,
Jan
Brossette‡
a,
Jan
Brossette‡
 a,
Harish
Jangra
a,
Harish
Jangra
 a,
Yin
Wei
a,
Yin
Wei
 b,
Min
Shi
b,
Min
Shi
 bc,
Hendrik
Zipse
bc,
Hendrik
Zipse
 *a and
Armin R.
Ofial
*a and
Armin R.
Ofial
 *a
*a
aDepartment Chemie, Ludwig-Maximilians-Universität München, Butenandtstr. 5-13, 81377 München, Germany. E-mail: zipse@cup.uni-muenchen.de; ofial@lmu.de
bState Key Laboratory of Organometallic Chemistry, Center for Excellence in Molecular Synthesis, University of Chinese Academy of Sciences, Shanghai Institute of Organic Chemistry, Chinese Academy of Sciences, 345 Lingling Road, Shanghai, P. R. China
cKey Laboratory for Advanced Materials and Institute of Fine Chemicals, School of Chemistry & Molecular Engineering, East China University of Science and Technology, Meilong Road No. 130, 200237 Shanghai, P. R. China
First published on 14th October 2024
Abstract
The addition of phosphines (PR3) to Michael acceptors is a key step in many Lewis-base catalysed reactions. The kinetics of the reactions of ten phosphines with ethyl acrylate, ethyl allenoate, ethyl propiolate, ethenesulfonyl fluoride, and ethyl 2-butynoate in dichloromethane at 20 °C was followed by photometric and NMR spectroscopic methods. The experimentally determined second-order rate constants k2 show that electronic effects in sterically unencumbered phosphines affect their nucleophilicity towards different classes of Michael acceptors in the same ordering. Michael acceptors with sp-hybridised electrophilic centres, however, are less susceptible to changes in the PR3 nucleophilicity than those with sp2-hybridised reactive sites. Linear correlations of lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k2 from this work with published rate constants for SN2 and SN1 reactions as well as with Brønsted basicities and fugalities for PR3 demonstrate the generality of the detected reactivity trends. Computed reaction barriers (ΔG‡calc) as well as reaction energies (ΔGadd) for Michael adduct formations show excellent correlations with experimentally obtained reaction barriers (ΔG‡exp) corroborating the interpretation of the kinetic data and revealing the philicity/fugality features of the reactants in phospha-Michael additions.
k2 from this work with published rate constants for SN2 and SN1 reactions as well as with Brønsted basicities and fugalities for PR3 demonstrate the generality of the detected reactivity trends. Computed reaction barriers (ΔG‡calc) as well as reaction energies (ΔGadd) for Michael adduct formations show excellent correlations with experimentally obtained reaction barriers (ΔG‡exp) corroborating the interpretation of the kinetic data and revealing the philicity/fugality features of the reactants in phospha-Michael additions.
Introduction
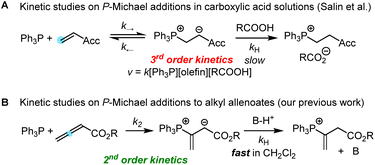
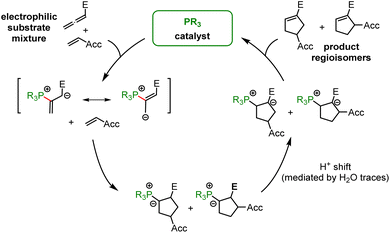
Addition of tertiary phosphines to electron-deficient π-systems generates zwitterionic intermediates which can be trapped directly or after isomerisation with various types of electrophilic reagents for carbon–carbon bond-formation. Thus, Horner's anionic acrylonitrile polymerisation,1 Rauhut–Currier reactions, Morita–Baylis–Hillman reactions,2–4 Lu's (3 + 2) cycloadditions, Kwon's [4 + 2] annulations5 and many other useful Lewis-base catalysed reactions6 share phospha-Michael additions7 as initiating steps in their catalytic cycles toward complex, functionalised products.8 Chiral phosphine catalysts have enabled enantioselective versions of these transformations.9 Though some phospha-Michael additions have recently been exploited for bioorthogonal reactions to detect α,β-unsaturated carbonyl groups in biomolecular targets,10 the reversibility of the endergonic phosphine additions to Michael acceptors has remained a challenge for kinetic studies.Protonation of the zwitterionic intermediate is a straightforward approach to render the phospha-Michael addition irreversible. The kinetics of phospha-Michael additions in protic and aprotic solvents with carboxylic acids as the proton sources were carefully investigated by Salin and co-workers (Scheme 1A).11–14 Generally, rate-determining proton transfer from carboxylic acids to the intermediate zwitterions gave rise to third-order kinetics (Scheme 1A).
Recently, we studied the kinetics of the adduct formation of PBu3 and PPh3 with alkyl and phenyl allenoates in dichloromethane solution.15 By utilising collidinium triflate and trialkylphosphonium triflates as the proton sources (BH+), the intermediate zwitterions were efficiently trapped in fast reactions. It, thus, became possible to determine second-order rate constants k2 for phosphine additions to allenoates, which allowed us to identify the impact of structural variation on the reactivity of these electrophiles (Scheme 1B).
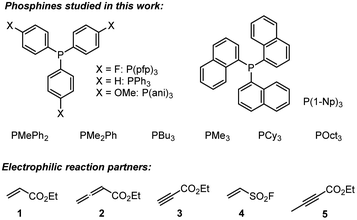
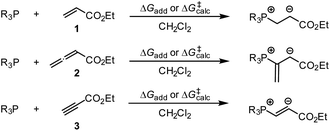
A complementary, systematic comparison of PR3 reactivities in phospha-Michael additions across different types of Michael acceptors is not available to date.16 We, therefore, set out to investigate the kinetics of PR3 additions to allenic, acetylenic and vinylic Michael acceptors. Herein, we present the analysis of the addition kinetics of ten phosphines to ethyl acrylate (1), ethyl allenoate (2), ethyl propiolate (3), ethenesulfonyl fluoride (4), and ethyl 2-butynoate (5) in dichloromethane at 20 °C (Scheme 2), which were followed by photometric and NMR spectroscopic methods. Given that these phosphine additions are generally considered to be the first step in PR3-catalysed reactions, kinetic investigations will also help to gain further insight into the key factors that control a manifold of organocatalytic reactions. Furthermore, quantum-chemical methods were employed to rationalise the reactivity ordering observed in the kinetic experiments.
Results and discussion
Products of the reactions of phosphines with the electrophiles 1–3
Horner and co-workers showed that stable, zwitterionic phospha-Michael adducts are obtained when PEt3 or PPh3 are combined with highly reactive Michael acceptors, such as 1,1-dicyanoethene.1 They noted, however, that the less Lewis acidic benzylidenemalononitrile (BMN) only forms Lewis adducts with trialkylphosphines (PMe3, PEt3, and PBu3) but not with PPh3. Photometric studies of the isolated adduct of benzylidenemalononitrile and PEt3 surprisingly showed that the UV-vis spectrum was identical to benzylidenemalononitrile alone. Horner explained this experimental observation by the dissociation of the Michael adduct in solution.1Efficient trapping of the initially formed zwitterionic phospha-Michael adducts is, therefore, a prerequisite to get to observable reaction products in solution and to generate conditions for reproducible kinetic measurements. Hence, we started our preparative investigations by NMR characterisations of relevant protonated Michael adducts.
The Michael addition of PPh3 to acrylate 1 was first reported by Hoffmann, who used triphenylphosphine hydrobromide that reacted with ethyl acrylate (1) within 15 min in acetonitrile.17 We used pre-formed triphenylphosphonium triflate (TPPT) to characterise the products of its reactions with the electrophiles 1–4 by NMR spectroscopic and HRMS methods (Scheme 3).
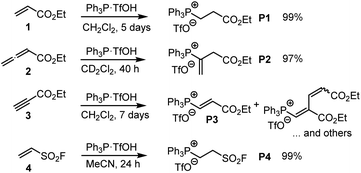 | ||
| Scheme 3 Generation of phosphonium triflates P1–P4 by reaction of PPh3·TfOH (TPPT) with the Michael acceptors 1–4 (at ambient temperature). | ||
TPPT reacted slowly but selectively with ethyl acrylate (1) to furnish within five days almost quantitatively the phosphonium triflate P1, which was isolated in a yield of 99%.18 The analogous reaction of TPPT with ethyl allenoate (2) in CD2Cl2 generated the vinylphosphonium triflate (P2) in a yield of 97%.15 The reaction of TPPT with Michael acceptor 3 mainly produced the acceptor-substituted vinyl phosphonium salts P3. The NMR spectra and in particular the HRMS analytical data showed that also 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 products (as a mixture of E- and Z-isomers) were formed in significant amounts, which could not be separated from the 1
1 products (as a mixture of E- and Z-isomers) were formed in significant amounts, which could not be separated from the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 adduct P3. Ethenesulfonyl fluoride (ESF, 4) is a considerably stronger electrophile than 1–3. Accordingly, 4 reacted already within 24 h quantitatively with TPPT to yield the phosphonium triflate P4 (99% yield of isolated product).
1 adduct P3. Ethenesulfonyl fluoride (ESF, 4) is a considerably stronger electrophile than 1–3. Accordingly, 4 reacted already within 24 h quantitatively with TPPT to yield the phosphonium triflate P4 (99% yield of isolated product).
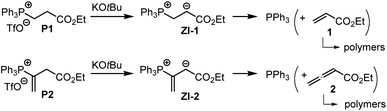
The associations of triphenylphosphine with Michael acceptors 1–4 are highly reversible if the reactions are performed without an appropriate proton source that efficiently traps the incipient, zwitterionic Lewis adducts. Attempts to generate the zwitterions ZI-1 and ZI-2 by deprotonation of the phosphonium salts P1 and P2, respectively, with potassium t-butoxide in d6-DMSO gave rise to rapid retro-Michael additions (Scheme 4). The release of free PPh3 from P1 and P2 was unequivocally detected by 1H, 13C, and 31P NMR spectroscopic analysis of the reaction mixtures (ESI, Fig. S19–S24†). The electrophiles 1 and 2 cannot be recovered under these reaction conditions. However, owing to a lack of NMR signals in the olefinic region and the occurrence of various new resonances in the aliphatic region, we assume that 1 and 2 rather undergo anionic polymerisations. These observations indicate that Lewis acid/base adduct formation between triphenylphosphine and the Michael acceptors 1 or 2 are endergonic.
To investigate the kinetics of the first step of the phosphine-catalyzed reactions with Michael acceptors, we have, therefore, decided to combine phosphines PR3 with the relevant electrophiles in the presence of proton sources that are able to intercept the initially formed zwitterions by fast protonation. The next section, therefore, shows how we identified Brønsted acids that reliably trapped the zwitterionic adducts but did not influence the reactivities of two reaction partners in the phospha-Michael addition.
Choice of proton sources as trapping reagents for the intermediate zwitterions
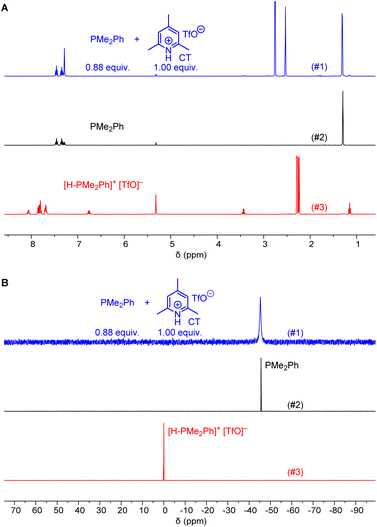
Ohmori and colleagues showed that the reaction of PPh3 with 1 (in CH2Cl2) can be performed under neutral conditions when 2,6-lutidinium perchlorates or tetrafluoroborates are used as proton sources.19 Lutidinium ions are only weak acids (pKa = 14.16 in MeCN)20 and it can be expected that they are neither able to protonate PPh3 (pKaH = 7.62 in MeCN)20 nor the Michael acceptor 1.Given that we needed a proton source to cover the Brønsted basicity range from P(pfp)3 to PMe2Ph (pKaH = 12.64 in MeCN) without affecting the reactivity of the phosphines, we expected that the even less acidic 2,4,6-collidinium triflate (pKa = 15.00 in MeCN)20 would be a practical trapping reagent for kinetic measurements. NMR spectroscopic studies in CD2Cl2 were carried out to assess whether the known relative acidities in acetonitrile are transferable to those in dichloromethane solution. The 1H NMR spectrum of a mixture of PMe2Ph with a slight excess of 2,4,6-collidinium triflate (CT) showed only resonances that could be assigned to both individual components in the mixture. Resonances for the phenyl group in [H-PMe2Ph]+ at δ > 7.5 ppm were not detected, and also the CH3 resonance of PMe2Ph at δ = 1.31 ppm did not shift when mixed with CT (Fig. 1A). Accordingly, the 31P NMR spectrum of a mixture of CT with PMe2Ph (0.9 equiv.) in CD2Cl2 showed that the detected chemical shift (δP = −45.6 ppm) corresponds to free PhMe2P and is not shifted towards the resonance for the protonated form (δP = 0.0 ppm, Fig. 1B). An analogous 1H and 31P NMR study for a mixture of the less basic PMePh2 (pKaH = 9.97 in MeCN)20 and CT is presented in the ESI (Fig. S3 and S4†) and shows, accordingly, that CT does not protonate PMePh2 in dichloromethane.
Further NMR studies were carried out to elucidate possible interactions of CT additives with the Michael acceptors 1–3. Fig. S7–S9† (ESI) illustrate that the 1H NMR chemical shifts of the acrylate 1, the allenoate 2, and the propiolate 3, respectively, did not undergo changes when mixed with CT in CD2Cl2. The resonances assigned to CT remained unchanged, which indicates that this proton source does not interact with the electrophiles. Given that interactions of CT were neither observable with the electrophilic Michael acceptors 1–3 nor with those phosphines PR3 with basicities lower than that of PMe2Ph (pKaH < 12.64 in MeCN), it can be expected that CT will be a suitable zwitterion intercepting reagent for kinetic experiments in dichloromethane solution.
Kinetic measurements for reactions of electrophiles with the more basic trialkylphosphines PMe3, PCy3 and POct3 were carried out by in situ liberation of a certain amount of free PR3 from trialkylphosphonium triflates by adding known amounts of the strong Brønsted base triethylamine (TEA) to the solutions in dichloromethane. The detection of only a single 31P NMR signal (in CD2Cl2) indicates quantitative deprotonation of [H-PR3]+ by TEA (ESI, Fig. S16–S18†). By using the thus generated solutions, the reversibly formed adducts of the reactions of the electrophiles 1–3 with PMe3, PCy3 and POct3, respectively, were efficiently trapped by the conjugate Brønsted acids of the studied PR3 nucleophiles. Because handling and further dilution steps of the trialkylphosphine stock solutions were avoided by this procedure, also oxidation prone PR3 could be studied under reliable conditions and delivered reproducible kinetic data.
Comparing the heats of formation for the parent allene (ΔfH = +192.1 kJ mol−1) with that for propyne (ΔfH = +185.4 kJ mol−1) shows that the alkyne is the thermodynamically favored isomer.21 We, therefore, tested whether the allene derivative 2 can isomerise to the acetylene derivative 5 under the conditions of the kinetic experiments. The 1H NMR spectra of TEA + 2 and TEA + 5 mixtures in CD2Cl2, which were stored at ambient temperature overnight (ESI, Fig. S11 and S12†), remained unchanged, however, indicating that free TEA is not able to equilibrate the allenoate 2 with the corresponding alkynoate tautomer 5, or vice versa.
Furthermore, comparing 1H NMR spectra of the mixtures of triethylammonium triflate (TEAT), which is generated during the in situ liberation of PR3, and Michael acceptors 1, 2, and 5 (in CD2Cl2) with those of the individual compounds in the same solvent showed that TEAT (possible proton source) does not interact with the electrophiles 1, 2, and 5 (ESI, Fig. S13–S15†). Interestingly, also mixtures of tributylphosphonium triflate (TBPT) with ethyl acrylate (1) show 1H NMR spectra, which reflect the resonances of the individual compounds (ESI, Fig. S10†), thus excluding significant electrophile activation by the presence of the TBPT proton source.
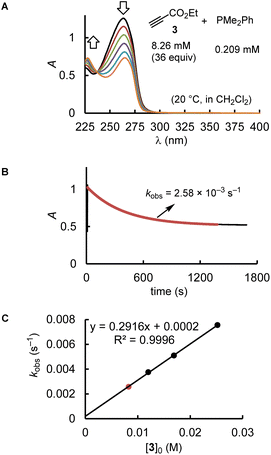
Kinetics
Depending on the spectroscopic properties of the reagents, the kinetics of PR3 additions to the electrophiles 1–3 were monitored by using either photometry or NMR spectroscopy.The majority of the kinetics of reactions of 2 and 3 with phosphines in dichloromethane at 20 °C were determined by following absorption changes in the UV-range. For a straightforward evaluation of the absorption decay curves, we used one of the reaction partners in at least 10-fold excess relative to the initial concentration of the minor compound. This made it possible that first-order rate constants kobs (s−1) could be derived from fitting the mono-exponential function A = A0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−kobst) + C to the experimentally observed decrease of the absorption of the minor compound. Determination of kobs at four different concentrations of the excess reaction partner enabled us to calculate the second-order rate constants k2 (M−1 s−1) from the slope of the linear regression line of kobsvs. [PR3]0 or [electrophile]0. Furthermore, the linearity of both types of plots, that is, kobsvs. [PR3]0 and kobsvs. [electrophile]0, indicates the operation of a rate law for the overall reaction, which is first order in [PR3] and first order in [electrophile].
exp(−kobst) + C to the experimentally observed decrease of the absorption of the minor compound. Determination of kobs at four different concentrations of the excess reaction partner enabled us to calculate the second-order rate constants k2 (M−1 s−1) from the slope of the linear regression line of kobsvs. [PR3]0 or [electrophile]0. Furthermore, the linearity of both types of plots, that is, kobsvs. [PR3]0 and kobsvs. [electrophile]0, indicates the operation of a rate law for the overall reaction, which is first order in [PR3] and first order in [electrophile].
Fig. 2 uses the relatively slow reaction of 3 with PMe2Ph to illustrate the workflow for kinetic measurements by conventional photometric equipment and their subsequent evaluation. The kinetics of faster reactions (t1/2 < 40 s) were followed by using stopped-flow spectrophotometer systems and analysed analogously. The sequential mixing option of the stopped-flow instrument was used to study the kinetics of the fast reactions of PMe3 with the electrophiles 1, 2, and 4. At mixer 1, PMe3 was liberated by deprotonation of trimethylphosphonium tetrafluoroborate with a substoichiometric amount of TEA. The thus prepared nucleophile solution was then mixed at mixer 2 with the solution of 1, 2, or 4. Details for the individual kinetics are given in the ESI.†
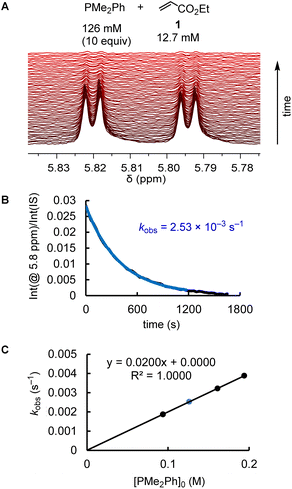
The kinetics of further phosphine–electrophile reactions, in particular those which involved phosphines with aryl groups, were more accessible through the use of NMR techniques.22 Tracing the time-dependent changes in the 1H NMR spectra was used, for example, to follow the kinetics of the PMe2Ph addition to ethyl acrylate (1) (Fig. 3). CT trapped the intermediate zwitterions. Added mesitylene served as the internal integration standard. The experiment shown in Fig. 3A was repeated at different CT concentrations at otherwise identical conditions. For [CT] = 21.4, 37.1, and 73.3 mM, the observed first-order rate constants kobs were 2.53 × 10−3, 2.47 × 10−3, and 2.55 × 10−3 s−1, respectively (ESI, Table S10†). An analogous independency of kobs in the reaction of PBu3 + 1 was observed when enhancing the TBPT concentration (ESI, Table S11†). Thus, in accord with the previous NMR investigations on binary CT (or TBPT) mixtures with either phosphines or electrophiles, the observed rate constant kobs remained unchanged within the experimental error limit, which corresponds to a zeroth order kinetics with regard to the concentration of the proton source. This observation underpins again that the nature of the proton sources selected in this work did not affect the kinetics of the phospha-Michael additions we aimed to investigate.
Phosphines PR3 were used as the excess compounds when the decay of the electrophile was followed by 1H NMR spectroscopy (Fig. 3). An inverse concentration ratio, that is, with the electrophiles as the excess compounds, was employed for 31P NMR kinetic measurements. The kinetics for the combinations of PMePh2 with 1 gave k2 = 1.66 × 10−3 M−1 s−1 by 1H NMR (ESI, Table S9†) and k2 = 2.36 × 10−3 M−1 s−1 by 31P NMR spectroscopy (ESI, Table S8†), which agree within a factor of 1.4. Reaction monitoring of the kinetics of P(pfp)3 with ethyl allenoate (2) gave a k2(31P)/k2(1H) ratio of 1.1 (ESI, Tables S16 and S17†). For the reactions of PPh3 with ethyl propiolate 3 (ESI, Tables S28 and S29†), 1H NMR spectroscopy delivered a slightly higher k2 value than the 31P NMR spectroscopic reaction tracing [k2 = 1.04 × 10−2 M−1 s−1 (1H) vs. 7.05 × 10−3 M−1 s−1 (31P)]. In general, we considered rate constants determined by time-resolved 1H NMR spectroscopy to be more reliable than results from 31P NMR spectroscopic reaction monitoring because 1H NMR spectra were recorded with an internal integration reference. In subsequent correlations we, therefore, preferred to use k2 from 1H NMR kinetics if k2 for a given PR3 + electrophile pair was determined by both 1H and 31P NMR kinetics.
To further test the influence of the zwitterion trapping on the kinetics, we used two different proton sources (CT and TEAT) when following the kinetics of the reaction of PPh3 with ethyl acrylate (1) by 31P NMR spectroscopy (Table 1, entries 1 & 2). The individual linear correlations of kobs with [1]0 agreed so surprisingly well that we used the first-order rate constants from both series of kinetic measurements jointly to determine the second-order rate constant k2 for the PPh3 + 1 reaction (ESI, Table S6†).
In a next step, we sought to replace the proton source by an olefinic Michael acceptor, that is, a neutral carbon-centred electrophile. The highly electrophilic BMN (Mayr E = −9.42)23 was used by Lu and coworkers as a reaction partner for alkyl allenoates 2 in PPh3-catalysed cyclopentene syntheses.24 Recently, we could demonstrate that BMN reacts fast yet reversibly with PBu3.15 Generation of cycloadducts, therefore, requires initial PBu3 attack at the allenoate electrophile to be productive. Entries 3 and 4 in Table 1 show that the second-order rate constants k2 for reactions of ethyl acrylate (1) with PBu3 are identical (within an error margin of ±10%) and independent of whether proton (TBPT) or BMN trapping was used. Similar rate constants k2 (within ±10%) were also derived for the reaction of ethyl propiolate (3) with PMe2Ph when CT and BMN were compared as trapping reagents (entries 5 & 6). The results in Table 1, thus, corroborate that the proton sources used in the kinetic standard procedure to generate the data for Table 2 neither attenuated the reactivity of the PR3 nucleophiles nor enhanced the electrophilicity of the esters 1 and 3 by protonation.
| Phosphines PR3 | k 2 (M−1 s−1) | ||||
|---|---|---|---|---|---|
| Ethyl acrylate (1) | Ethyl allenoate (2) | Ethyl propiolate (3) | ESF (4) | Ethyl 2-butynoate (5) | |
| a In CH2Cl2, kinetics followed by photometric methods if not mentioned otherwise. b In CD2Cl2, kinetics followed by online 31P NMR spectroscopy. c In CD2Cl2, kinetics followed by online 1H NMR spectroscopy. d For the reaction of 2 with PPh3 in benzene activation parameters ΔH‡ = 14.8 kcal mol−1 and ΔS‡ = −19.6 cal mol−1 K−1 were reported in ref. 25, which correspond to a second-order rate constant of k2 = 2.9 × 10−3 M−1 s−1 (20 °C). | |||||
| P(pfp)3 | 2.22 × 10−5b | 3.43 × 10−3c | 2.86 × 10−3c | 4.23 × 10−1 | n.d. |
| PPh3 | 1.55 × 10−4b | 7.67 × 10−3c,d | 1.04 × 10−2c | 3.38 | 2.05 × 10−5b |
| P(ani)3 | 9.32 × 10−4b | 3.76 × 10−2 | 5.45 × 10−2 | n.d. | n.d. |
| PMePh2 | 1.66 × 10−3c | 6.12 × 10−2 | 6.28 × 10−2 | 8.76 | n.d. |
| PMe2Ph | 2.00 × 10−2c | 2.68 × 10−1 | 2.92 × 10−1 | 4.26 × 102 | n.d. |
| PBu3 | 5.83 × 10−2 | 6.35 × 10−1 | 9.61 × 10−1 | 7.99 × 102 | 5.71 × 10−3c |
| PMe3 | 1.24 × 10−1 | 9.69 × 10−1 | 9.56 × 10−1 | 2.07 × 103 | n.d. |
| PCy3 | 3.82 × 10−2c | 1.20 × 10−1 | 1.43 | n.d. | n.d. |
| POct3 | 5.45 × 10−2 | 7.24 × 10−1 | 2.69 | n.d. | n.d. |
| P(1-Np)3 | Too slowb | 8.00 × 10−6b | 8.46 × 10−5b | n.d. | n.d. |
Table 2 gathers the second-order rate constants k2 for the reactions of the phosphines PR3 with the electron-deficient π-systems in 1, 2, and 3.25 In addition, the kinetics of PR3 reactions with ESF (4) were included in the study. ESF (4) is a Michael acceptor that is known to be considerably more electrophilic than ethyl acrylate 1.26 Furthermore, we investigated the reactivity of ethyl 2-butynoate (5), an isomer of 2, towards PBu3 and PPh3.
As illustrated in Fig. 4, the second-order rate constants k2 in Table 2 show that ethyl acrylate (1) is a relatively weak electrophile towards phosphines PR3. The reactivities of PR3 towards ethyl allenoate (2) and ethyl propiolate (3) are at almost the same levels and generally exceed those towards ethyl acrylate (1) by one to two orders of magnitude. The reactivity of the terminal alkynyl π-system in the ethyl ester 3 is reduced by 2.5 to 3 orders of magnitude if a methyl substituent is added, as shown by the entries for ethyl 2-butynoate (5), which is even by a factor of 10 less reactive towards phosphines PR3 than ethyl acrylate (1).
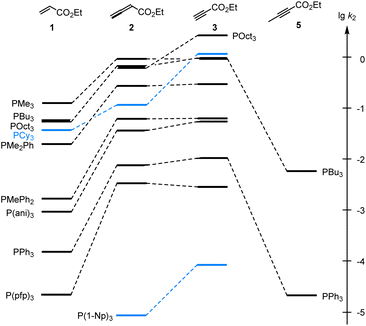 | ||
Fig. 4 Reactivities of PR3 towards the Michael acceptors 1, 2, 3, and 5 compared by the second-order rate constants (lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k2) for the formation of Michael adducts in dichloromethane at 20 °C (data from Table 2). k2) for the formation of Michael adducts in dichloromethane at 20 °C (data from Table 2). | ||
Significant changes in the relative order of PR3 reactivities are only observed for the sterically demanding phosphine PCy3,27 which catches up in reactivity with other trialkylphosphines when it adds to the terminal electrophilic carbons in 1 or 3. However, PCy3 reacts considerably slower than other trialkylphosphines with 2, in which the electrophilic reaction centre is the central carbon in the allene π-system and thus more difficult to access for the bulky PCy3 than for the sterically less demanding phosphines PMe3, PBu3 or POct3. As a consequence, rate constants for reactions of PCy3 were generally excluded in the subsequent correlation analyses, which were performed to gain further quantitative insight in structure–reactivity relationships for Michael additions of phosphines PR3. The same reasons that explain the k2(3)/k2(2) = 12 for PCy3 can be applied to rationalise the by one order of magnitude higher reactivity of P(1-Np)3 towards 3 (terminal electrophilic centre) than towards 2.
Correlation analysis
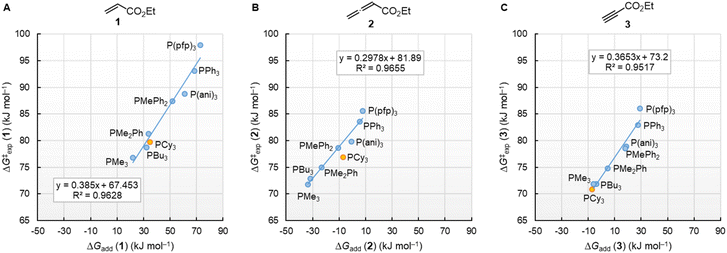
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k2) of the reactions with ethyl acrylate (1) can be used as a reference to compare the susceptibilities of the different types of electrophiles for variation of the phosphine reactivities. Fig. 5 shows that the relative trends are identical when changing from the sp2-hybridised electrophilic centre in 1 to the sp-hybridised reactive positions in 2 or 3. The slopes of 0.686 and 0.747 for the correlations with 2 and 3, respectively, illustrate however, that the increase in phosphine reactivity towards Michael acceptor 1 is only partially found in the faster reactions with the electron-deficient π-systems in 2 and 3. The lower susceptibility is not a consequence of the Reactivity-Selectivity-Principle, a concept that has been criticised several times before.28 This can be demonstrated through reactions of the phosphines PR3 with ESF (4), which are much faster than those with 1, 2, or 3. Yet, the linear plot of lg k2(4) vs. lg
k2) of the reactions with ethyl acrylate (1) can be used as a reference to compare the susceptibilities of the different types of electrophiles for variation of the phosphine reactivities. Fig. 5 shows that the relative trends are identical when changing from the sp2-hybridised electrophilic centre in 1 to the sp-hybridised reactive positions in 2 or 3. The slopes of 0.686 and 0.747 for the correlations with 2 and 3, respectively, illustrate however, that the increase in phosphine reactivity towards Michael acceptor 1 is only partially found in the faster reactions with the electron-deficient π-systems in 2 and 3. The lower susceptibility is not a consequence of the Reactivity-Selectivity-Principle, a concept that has been criticised several times before.28 This can be demonstrated through reactions of the phosphines PR3 with ESF (4), which are much faster than those with 1, 2, or 3. Yet, the linear plot of lg k2(4) vs. lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k2(1) shows constant selectivity (slope = 0.985). Rather, we interpret the different slopes in Fig. 5A–C to be a result of the different hybridisation of the electrophilic centres, which differentiate the sp2-hybridised reactive sites in 1 and 4 from those in the sp-hybridised 2 and 3.
k2(1) shows constant selectivity (slope = 0.985). Rather, we interpret the different slopes in Fig. 5A–C to be a result of the different hybridisation of the electrophilic centres, which differentiate the sp2-hybridised reactive sites in 1 and 4 from those in the sp-hybridised 2 and 3.
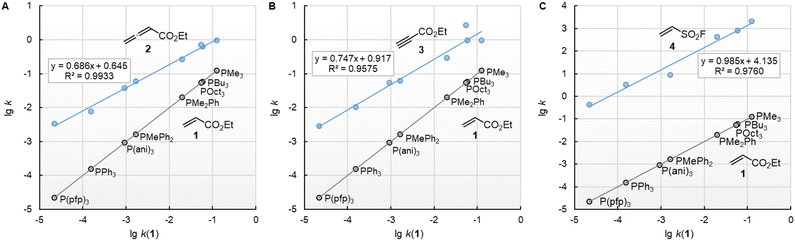 | ||
Fig. 5 Relative reactivities of PR3 towards (A) ethyl allenoate (2), (B) ethyl propiolate (3), and (C) ESF (4) referenced towards lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k(PR3 + 1). With rate constants k2 from Table 2, data for the sterically encumbered PCy3 was excluded when constructing the correlation lines. k(PR3 + 1). With rate constants k2 from Table 2, data for the sterically encumbered PCy3 was excluded when constructing the correlation lines. | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kFB), and methyl cation affinities (MCA)
kFB), and methyl cation affinities (MCA)
| PR3 | lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k2 k2 |
pKaHa | lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k2(EtI)b k2(EtI)b |
N Fe | lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kFBd kFBd |
||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | |||||
| a Acidities of R3P+H refer to H2O as reported in ref. 29a and 30, values in parentheses are acidities of R3P+H in MeCN as reported in ref. 20. b Calculated from second-order rate constants k2 (M−1 s−1) for reactions of PR3 with ethyl iodide in acetone at 35 °C reported in ref. 29b. c Phosphine nucleophilicities NFe towards iron-complex stabilised carbocations from ref. 31. d Calculated from the rate constants kFB (M−1 s−1) for the ligand exchange of R3P in R3P→BH3 complexes by quinuclidine in toluene at 30 °C reported in ref. 32. e N Fe of PEt2Ph is used because NFe for PMe2Ph has not been determined. f Calculated by DFT methods (ESI). | |||||||
| P(pfp)3 | −4.65 | −2.46 | −2.54 | 1.97 | — | 1.3 | −2.17 |
| PPh3 | −3.81 | −2.12 | −1.98 | 2.73 (7.62) | −4.42 | 1.95 | −2.59 |
| P(ani)3 | −3.03 | −1.42 | −1.26 | 4.57 (10.06) | −3.57 | 2.9 | −3.47 |
| PMePh2 | −2.78 | −1.21 | −1.20 | 4.65 (9.97) | — | — | −3.46 |
| PMe2Ph | −1.70 | −0.57 | −0.53 | 6.49 (12.64) | −3.12 | (3.3)e | −4.46 |
| PBu3 | −1.23 | −0.20 | −0.02 | 8.43 | −2.79 | 3.6 | −5.59 |
| PMe3 | −0.91 | −0.01 | −0.02 | 8.65 (15.48) | −2.65 | — | −5.44 |
| PCy3 | −1.42 | −0.92 | +0.16 | 9.70 | −2.68 | — | −5.60 |
| POct3 | −1.26 | −0.14 | +0.43 | 9.03f | — | — | — |
The nucleophilic reactivities of amines towards C-centred electrophiles have repeatedly been reported to correlate only poorly with their Brønsted basicities (pKaH).33,34 In contrast, the second-order rate constants for the attack of phosphines PR3 at Michael acceptors 1–3 in dichloromethane are linearly related to the phosphine basicities in water (Fig. 6). PCy3 deviates negatively from the correlation lines constructed for the remaining PR3 nucleophiles, and the reaction of PCy3 with the allenoate 2 is by more than a factor of 10 slower than expected based on its pKaH. The deviation of PCy3 from the correlation lines is less prominent for both electrophiles with a terminal reaction centre. Because available data for pKaH(MeCN) and pKaH(H2O) of PR3 correlate linearly (r2 = 0.9997, n = 5, ESI, Fig. S1†), we can assume that correlations of our reactivity data with pKaH(H2O) will also hold in aprotic polar solvents and will allow chemists to predict the reactivities of further sterically unencumbered phosphines towards neutral electrophiles. The slopes in the range of 0.49 to 0.34 indicate that only a part of the thermodynamic driving force of the protonation reactions is seen in the kinetics of PR3 additions to Michael acceptors.
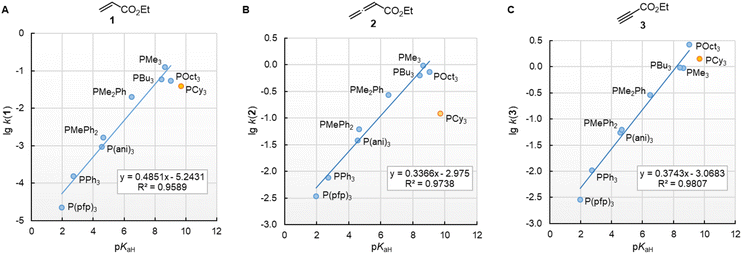 | ||
Fig. 6 Linear relationships of the second-order rate constants (lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k2, at 20 °C in dichloromethane) for reactions of R3P with the Michael acceptors (A) ethyl acrylate (1), (B) ethyl allenoate (2), and (C) ethyl propiolate (3) and the Brønsted basicities pKaH(H2O) of the phosphines R3P (with data from Table 3, data for the sterically encumbered PCy3 excluded when constructing the correlation lines). k2, at 20 °C in dichloromethane) for reactions of R3P with the Michael acceptors (A) ethyl acrylate (1), (B) ethyl allenoate (2), and (C) ethyl propiolate (3) and the Brønsted basicities pKaH(H2O) of the phosphines R3P (with data from Table 3, data for the sterically encumbered PCy3 excluded when constructing the correlation lines). | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k(EtI) (Fig. 7). For the electrophiles 1 and 3, the data point of PCy3 is close to the respective correlation line, which illustrates the similar steric demand for reactions of PR3 at terminal –CH2X,
k(EtI) (Fig. 7). For the electrophiles 1 and 3, the data point of PCy3 is close to the respective correlation line, which illustrates the similar steric demand for reactions of PR3 at terminal –CH2X, ![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CH2, and
CH2, and ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) CH groups. The slope of the correlation line is 1.7 for the olefinic Michael acceptor 1 (Fig. 7A), close to the typical slope of 2 observed when comparing nucleophile reactivities in SN1 reactions with those in SN2 reactions.35–37 The correlation lines for the sp-hybridised electrophiles 2 and 3 are more shallow. Their slopes in the range of 1.2 (Fig. 7B/C) are caused by the higher degree of reorganisation required to change the hybridisation at the reaction centre from a linear to a trigonal planar geometry.
CH groups. The slope of the correlation line is 1.7 for the olefinic Michael acceptor 1 (Fig. 7A), close to the typical slope of 2 observed when comparing nucleophile reactivities in SN1 reactions with those in SN2 reactions.35–37 The correlation lines for the sp-hybridised electrophiles 2 and 3 are more shallow. Their slopes in the range of 1.2 (Fig. 7B/C) are caused by the higher degree of reorganisation required to change the hybridisation at the reaction centre from a linear to a trigonal planar geometry.
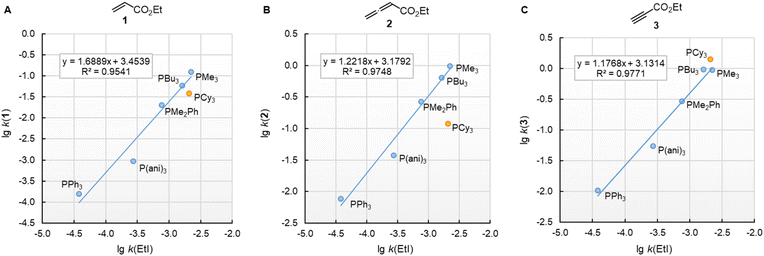 | ||
Fig. 7 Reactivities (lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k2) of PR3 towards (A) ethyl acrylate (1), (B) ethyl allenoate (2), and (C) ethyl propiolate (3) correlate linearly with the SN2 reactivity of PR3 towards ethyl iodide (in acetone at 35 °C, ref. 29b). With rate constants k2 from Table 3, data for the sterically encumbered PCy3 excluded when constructing the correlation lines. k2) of PR3 towards (A) ethyl acrylate (1), (B) ethyl allenoate (2), and (C) ethyl propiolate (3) correlate linearly with the SN2 reactivity of PR3 towards ethyl iodide (in acetone at 35 °C, ref. 29b). With rate constants k2 from Table 3, data for the sterically encumbered PCy3 excluded when constructing the correlation lines. | ||
Furthermore, rate constants of addition reactions of phosphines PR3 to iron-complex stabilised carbocations, such as [Fe(CO)3(C6H7)]+, were reported.31,38 These kinetic data were used by Kane-Maguire, Honig, and Sweigart to derive NFe parameters (Table 3), which describe the averaged nucleophilicity of a PR3 reagent towards such cationic complexes.31 The graphs in Fig. 8 demonstrate that the phosphine reactivities determined for reactions with 1, 2, and 3 are linearly related with the NFe descriptors.
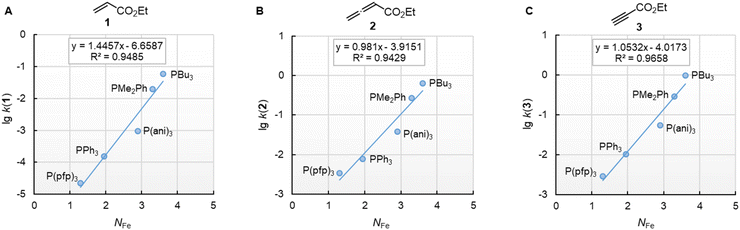 | ||
Fig. 8 Reactivities (lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k2) of PR3 towards (A) ethyl acrylate (1), (B) ethyl allenoate (2), and (C) ethyl propiolate (3) correlate linearly with NFe, which are nucleophilicity parameters for phosphines derived from reactions of PR3 with cationic electrophiles structurally similar to [Fe(CO)3(C6H7)]+, from ref. 31 and 38 With rate constants k2 from Table 3. For the PMe2Ph entries, the NFe of PEt2Ph was used. The correlation for ESF (4) is shown in Fig. S2 (ESI).† k2) of PR3 towards (A) ethyl acrylate (1), (B) ethyl allenoate (2), and (C) ethyl propiolate (3) correlate linearly with NFe, which are nucleophilicity parameters for phosphines derived from reactions of PR3 with cationic electrophiles structurally similar to [Fe(CO)3(C6H7)]+, from ref. 31 and 38 With rate constants k2 from Table 3. For the PMe2Ph entries, the NFe of PEt2Ph was used. The correlation for ESF (4) is shown in Fig. S2 (ESI).† | ||
Thus, the rate constants determined in this work for the reactions of PR3 phosphines with neutral Michael acceptors correlate both with reported phosphine reactivities towards SN2 and SN1 substrates. Given that the molecular structures of ethyl iodide and [Fe(CO)3(C6H7)]+ ion are unlike the Michael acceptors studied in this work, we can conclude that the reactivities of the PR3 nucleophiles determined towards Michael acceptors 1–3 are generally applicable.
The isoelectronic relation between H3C-X and [H3B-X]− triggered our interest to compare the reactivities of the phosphines PR3 at carbon with those at boron centres. Recently, Lloyd-Jones and colleagues studied the rate constants of quinuclidine displacement of R3P–BH3 adducts in toluene at 30 °C.32 They reported mechanistic evidence consistent with an SN2-like process at the boron-centre. The Lloyd-Jones group also derived an increment system of ‘ligand nucleofugality values 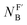 for phosphines PR3 to describe the structural factors that influence the leaving group abilities. The NFB values correlate excellently with the pKaH values of PR3 in water. The linear relationship spans over a range of 11 pKa units (n = 12, r2 = 0.9956) and comprises P(pfp)3 as the least basic and PCy3 as the most basic phosphine.32
for phosphines PR3 to describe the structural factors that influence the leaving group abilities. The NFB values correlate excellently with the pKaH values of PR3 in water. The linear relationship spans over a range of 11 pKa units (n = 12, r2 = 0.9956) and comprises P(pfp)3 as the least basic and PCy3 as the most basic phosphine.32
In this work, we found that also the reactivities of phosphines towards Michael acceptors correlate linearly with their pKaH values (cf.Fig. 6). Thus, the stage was set for establishing a relationship between nucleophilicities and nucleofugalities of PR3 by combining the rate constants for adduct formation of PR3 with Michael acceptors with the rate constants for the quinuclidine displacement of PR3 in R3P-borane complexes (kFB).32Fig. 9 shows an inverse linear correlation for the phosphines in both reaction series. The weakest nucleophile P(pfp)3 is the most reactive nucleofuge, and the relation is vice versa for the highly nucleophilic PMe3 or PBu3. Depending on the steric environment at the electrophilic centres of the Michael acceptors, PCy3 is close to the linear correlation for the sterically unencumbered PR3 species (as for 1 and 3) or has been determined to be a weaker nucleophile than expected on the basis of its nucleofugality lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) kFB (as for 2).
kFB (as for 2).
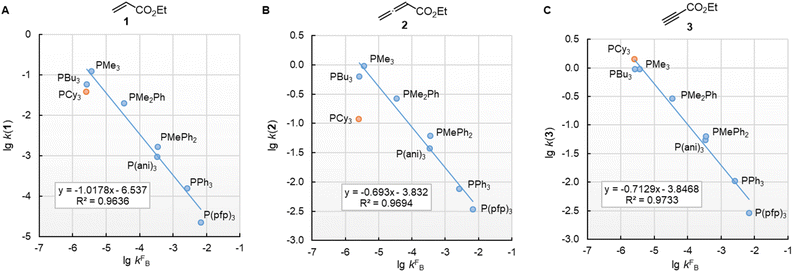 | ||
Fig. 9 Correlation of PR3 reactivity (lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) k2 in dichloromethane) towards (A) ethyl acrylate (1), (B) ethyl allenoate (2), and (C) ethyl propiolate (3) with the ligand nucleofugality of R3P from R3P→BH3 complexes (external nucleophile: quinuclidine, in toluene at 30 °C) from ref. 32. With rate constants kFB from Table 3, data for PCy3 excluded when constructing the correlation lines. k2 in dichloromethane) towards (A) ethyl acrylate (1), (B) ethyl allenoate (2), and (C) ethyl propiolate (3) with the ligand nucleofugality of R3P from R3P→BH3 complexes (external nucleophile: quinuclidine, in toluene at 30 °C) from ref. 32. With rate constants kFB from Table 3, data for PCy3 excluded when constructing the correlation lines. | ||
Quantum-chemical analysis
Previous quantum-chemical studies of the PMe3/methyl allenoate addition in benzene gave significantly different results: the addition was reported to be almost thermoneutral45b or endergonic (ΔGadd = +40.6 kJ mol−1).25,45a This ambiguity in calculating the driving force of a relatively simple model reaction is an indication of the importance of the computational methods used. Hence, we started by investigating the influence of quantum-chemical methods on the thermodynamics of the PMe3 addition to ethyl allenoate (2) by using different basis sets, electronic structure methods, and solvation models (see ESI† for details). We found that the combination of the MN15 functional with the triple-ζ basis set def2-TZVPP and the implicit solvation model SMD showed reliable performance. Hence, this combination was used for all quantum-chemical calculations performed in this work.46Methyl cation affinities (MCA)47,48 often characterise the reactivity of nucleophiles (Nuc:) towards C-centred electrophiles49 better than pKaH values, which reflect the thermodynamics of +Nuc–H bond formations. We, therefore, calculated MCAs for phosphines PR3, as shown in Scheme 5, from the Gibbs reactions energies of methylation reactions in dichloromethane (MCA = −ΔG298) (see Table 4 and ESI† for details).
 | ||
| Scheme 5 Reaction scheme for the calculation of PR3 methyl cation affinities (MCA) in dichloromethane. | ||
| PR3 | MCAa | Ethyl acrylate (1) | Ethyl allenoate (2) | Ethyl propiolate (3) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ΔG‡expb | ΔG‡calcc | ΔGaddd | ΔG‡expb | ΔG‡calcc | ΔGaddd | ΔG‡expb | ΔG‡calcc | ΔGaddd | ||
| a MCA (= −ΔG298) calculated according to Scheme 5 at the SMD(DCM)/MN15/def2-TZVPP level of theory at 298.15 K. b Gibbs activation energies ΔG‡exp calculated from the experimentally determined second-order rate constants k2 (20 °C) in Table 2 by using the Eyring equation. c Gibbs activation energies ΔG‡calc of the reactions in Scheme 6 calculated at the SMD(DCM)/MN15/def2-TZVPP level of theory at 298.15 K. d Gibbs reaction energies ΔGadd of the reactions in Scheme 6 calculated at the SMD(DCM)/MN15/def2-TZVPP level of theory at 298.15 K. | ||||||||||
| P(pfp)3 | 402.8 | 97.9 | 90.8 | 73.0 | 85.6 | 88.6 | 7.7 | 86.0 | 89.8 | 29.3 |
| PPh3 | 418.6 | 93.1 | 89.9 | 68.5 | 83.6 | 87.7 | 5.5 | 82.9 | 87.9 | 27.7 |
| P(ani)3 | 425.7 | 88.8 | 86.2 | 61.1 | 79.8 | 87.5 | −0.8 | 78.9 | 84.6 | 18.6 |
| PMePh2 | 434.5 | 87.4 | 86.5 | 51.8 | 78.6 | 87.8 | −10.8 | 78.5 | 86.7 | 18.1 |
| PMe2Ph | 448.6 | 81.3 | 80.6 | 33.9 | 75.0 | 83.7 | −23.3 | 74.8 | 82.2 | 4.6 |
| PBu3 | 459.7 | 78.7 | 79.2 | 32.2 | 72.9 | 83.6 | −31.8 | 71.9 | 79.7 | −3.6 |
| PMe3 | 466.1 | 76.8 | 79.2 | 22.0 | 71.8 | 82.7 | −33.6 | 71.9 | 80.2 | −5.9 |
| PCy3 | 473.0 | 79.7 | 81.5 | 34.7 | 76.9 | 81.9 | −7.1 | 70.9 | 71.9 | −7.2 |
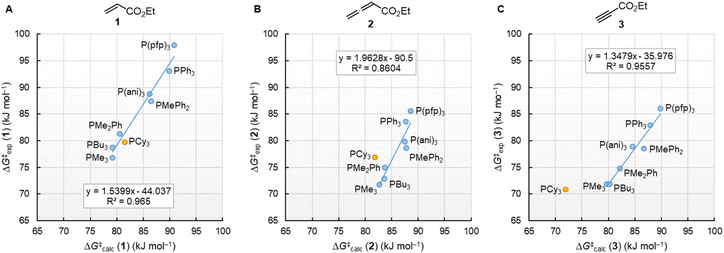
Fig. 10 illustrates that the experimentally determined Gibbs activation energies ΔG‡exp of PR3 additions to Michael acceptors 1, 2, and 3 (20 °C, CH2Cl2), except for PCy3, correlate linearly with the quantum-chemically calculated MCAs. Thus, we can conclude that the easily calculated thermodynamics of methylation reactions can be used to predict relative nucleophilicities of sterically unencumbered PR3 also towards other classes of C-electrophiles, such as electron-deficient π-systems.
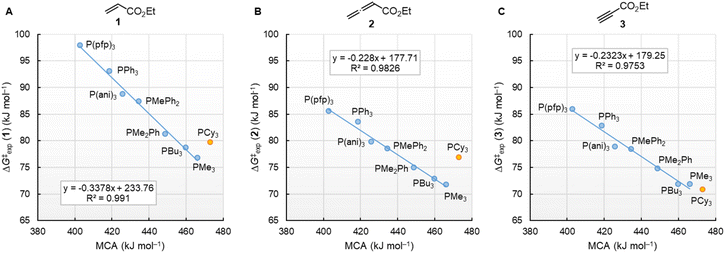 | ||
| Fig. 10 Correlation of experimental Gibbs activation energies ΔG‡exp with computed MCA values of PR3 additions to (A) ethyl acrylate (1), (B) ethyl allenoate (2), and (C) ethyl propiolate (3) in dichloromethane. With energies from Table 4, data for the sterically encumbered PCy3 excluded when constructing the correlation lines. | ||
By using the same DFT level of theory as for the MCA calculations, we then analysed the energetics of PR3 additions to Michael acceptors 1, 2, and 3 (Scheme 6) by calculating the reaction barriers ΔG‡calc and the Gibbs reaction energies for the addition step ΔGadd (Table 4).
 | ||
| Scheme 6 Gibbs activation (ΔG‡calc) and reaction energies (ΔGadd) of PR3 additions to Michael acceptors 1–3. | ||
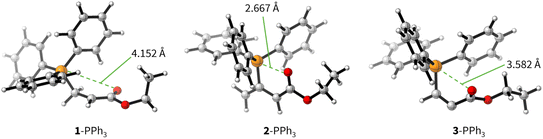
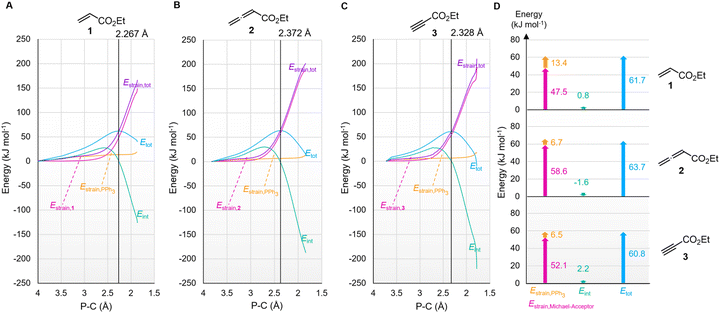
The positive ΔGadd values for PR3 additions to 1 (Table 4) are in accord with the experimentally observed reversibility of these reactions. For 2 and particularly 3 only the most reactive and Lewis basic phosphines react exergonically. In general, PR3 additions to the allenoate 2 are energetically more favourable than the corresponding reactions of phosphines with 1 or 3. We rationalise the differences in the stability of the zwitterionic PR3-adducts derived from 1, 2, and 3 by the variable extent of attractive P⋯O interactions in the adducts.25Fig. 11 depicts the optimised geometries of the adducts of 1, 2, or 3 with PPh3, the most relevant phosphine in organocatalysis. The computed P–O distances in the PPh3 adducts of 2, 3, and 1 follow the trend seen in ΔGadd: the shorter the P–O distance the more stable is the adduct.
The correlation lines in Fig. 12 indicate that the activation barriers (ΔG‡exp) of phosphine additions to the vinylic, allenic, and acetylenic electrophiles decrease systematically as the thermodynamic driving forces (ΔGadd) increase. However, the slopes in Fig. 12A–C reflect that only 39%, 30%, and 37% of the product stabilising effects are found in the transition states (TS) of these phospha-Michael additions.
 | ||
| Fig. 12 Correlations of ΔG‡exp (20 °C) for PR3 additions to (A) 1, (B) 2, and (C) 3 in dichloromethane with the respective reaction energies ΔGadd. With energies from Table 4, data for the sterically encumbered PCy3 excluded when constructing the correlation lines. | ||
Neglecting the effect of the small temperature difference between experimental and calculated energies (20 °C vs. 25 °C), the quantum-chemically calculated reaction barriers (ΔG‡calc) for phosphine additions to 1, 2, and 3 are within a range of ±10 kJ mol−1 of the experimentally determined Gibbs activation energies ΔG‡exp (Table 4). The excellent linear correlations of ΔG‡exp with ΔG‡calc in Fig. 13 corroborate the interpretation that the experimentally measured second-order rate constants k2 reflect the initial phosphine addition to the electron-deficient reaction partners. We note, however, that the regression lines for all three Michael acceptors show slopes significantly larger than unity, which implies that the 20 kJ mol−1 wide range for ΔG‡exp is compressed to a width of only 10 kJ mol−1 in the DFT calculations.
Transition state (TS) geometries for the addition of PPh3 to Michael acceptors 1, 2, and 3 are shown in Fig. 14. In contrast to the PPh3 adduct with 2, where the attractive P⋯O interaction was identified as a key stabilising factor, the P⋯O distance in the TS geometries of PPh3 reactions with 1, 2, and 3 are generally >3.5 Å and exceed the sum of the van der Waals radii of oxygen and phosphorus (3.22 Å, with O: 1.52 Å and P: 1.80 Å).50 The P–C bond formation is slightly more advanced in TS-1-PPh3 (P–C distance: 2.267 Å) than in TS-2-PPh3 (2.372 Å) or TS-3-PPh3 (2.328 Å), which indicates a later TS for the addition of PPh3 to 1 than for the analogous reaction with 2 and 3. Likewise, charge separation (NBO analysis) between PPh3 and the respective electrophile in the TS is found to be already larger for acrylate 1 than for 2 or 3: the cumulative partial charges in TS-1-PPh3 are ±0.492 and amount to only ±0.396 in TS-2-PPh3 and TS-3-PPh3, respectively. The origin of the variations in the reaction barrier (ΔG‡) were subsequently investigated by using the Marcus eqn (1) to calculate intrinsic barriers (ΔG‡0).43
 | (1) |
The intrinsic barriers ΔG‡0 (Table 5) obtained by combining experimental or theoretically calculated reaction barriers with the DFT-calculated ΔGadd show identical trends. The ΔG‡0 for reactions with the Michael acceptor 1, which changes hybridisation from sp2 to sp3 at the reaction centre, are significantly lower than those for analogous PR3 additions to 2 and 3, which involve the need for a higher degree of reorganisation owing to the change from sp- to sp2-hybridisation at the electrophilic centre (see Table 5). Nevertheless, the more favourable reaction energies ΔGadd for PR3 additions to 2 and 3 give rise to the overall lower reaction barriers (ΔG‡) and thus faster reaction rates, despite higher intrinsic barriers than for PR3 additions to the acrylate 1.
| PR3 | Ethyl acrylate (1) | Ethyl allenoate (2) | Ethyl propiolate (3) | |||
|---|---|---|---|---|---|---|
| ΔG‡0,exp | ΔG‡0,calc | ΔG‡0,exp | ΔG‡0,calc | ΔG‡0,exp | ΔG‡0,calc | |
| P(pfp)3 | 55.4 | 47.3 | 81.7 | 84.7 | 70.6 | 74.4 |
| PPh3 | 53.4 | 49.8 | 80.8 | 84.9 | 68.3 | 73.4 |
| P(ani)3 | 53.9 | 51.1 | 80.2 | 87.9 | 69.3 | 75.0 |
| PMePh2 | 58.6 | 57.7 | 83.9 | 93.1 | 69.2 | 77.4 |
| PMe2Ph | 63.2 | 62.5 | 86.3 | 95.0 | 72.5 | 79.9 |
| PBu3 | 61.6 | 62.1 | 88.1 | 98.9 | 73.7 | 81.5 |
| PMe3 | 65.3 | 67.8 | 87.8 | 98.8 | 74.8 | 83.1 |
| PCy3 | 61.1 | 63.0 | 80.4 | 85.4 | 74.5 | 75.5 |
The origin of the characteristic differences in the intrinsic barriers in the reaction series for 1 (ΔG‡0,exp = 53 to 65 kJ mol−1), 2 (80 to 88 kJ mol−1), and 3 (68 to 75 kJ mol−1) were further scrutinised by analysing deformation energies according to the activation strain model.51 The P–C distance (highlighted in the TS geometries in Fig. 14) was used as the reaction coordinate to analyse the activation strain energetics for the addition of PPh3 to Michael acceptors 1, 2, and 3 (Fig. 15). The calculated overall deformation energies (Estrain,tot) are dominated by the deformation energies (Estrain) of the electrophiles 1–3, while the deformation energies of PPh3 are comparatively small. The deformation energy for Michael acceptor 1 (47.5 kJ mol−1) is significantly smaller than Estrain for Michael acceptors 2 (58.6 kJ mol−1) or 3 (52.1 kJ mol−1), in accord with the ordering of the Marcus intrinsic barriers in Table 5 (53.4 kJ mol−1 for 1 + PPh3, 68.3 kJ mol−1 for 3 + PPh3, and 80.8 kJ mol−1 for 2 + PPh3). For all reactions in Fig. 15, the interaction energies (Eint) are destabilising at early stages of the P⋯C bond-formation and only become stabilising when approaching the TS region.
Conclusion
Phosphine additions to electron-deficient π-systems play a key role in many Lewis-base catalysed organic reactions. In this work, we determined second-order rate constants k2 for the additions of differently substituted tertiary phosphines PR3 to ethyl acrylate, ethyl allenoate, and ethyl propiolate in dichloromethane at 20 °C. The reactivities of PR3 quantified in this way correlate linearly with a range of PR3 properties, for example their SN2 and SN1 reactivities towards other types of electrophilic reaction partners or their Brønsted and Lewis basicities. In addition, the experimentally determined Gibbs activation energies correlate with theoretically calculated barriers for the phospha-Michael additions as well as with theoretically calculated reaction energies in dichloromethane (SMD solvent model) suggesting the potential to anchor future quantum-chemical modeling of PR3 reactions to experiments.Gibbs energy profiles for the phospha-Michael addition reactions can be constructed from the experimental Gibbs activation energies (ΔG‡) and the DFT-calculated Gibbs reaction energies (ΔGadd). Fig. 16 shows the energy profiles for reactions of 1, 2, or 3 with PPh3, which is the most frequently used phosphine catalyst in organocatalytic transformations. The energy profiles for PPh3 additions to acrylate 1 and allenoate 2 (or propiolate 3) immediately reveal that the addition barriers are surprisingly similar, while the reaction energies are largely different (Fig. 16). The by 27.4 kJ mol−1 higher intrinsic barrier ΔG‡0,exp for the PPh3 addition to 2 than to 1 (cf.Table 5) largely compensates the effect of the higher thermodynamic driving force for the adduct formation with 2 (0.5ΔΔGadd = 31.5 kJ mol−1). As a consequence, the energetic barrier for the retroaddition of the endergonic 1+PPh3 reaction is only 24.6 kJ mol−1. In contrast, the analogous dissociation of the 2 + PPh3-adduct proceeds over an energetic barrier of 78.1 kJ mol−1.
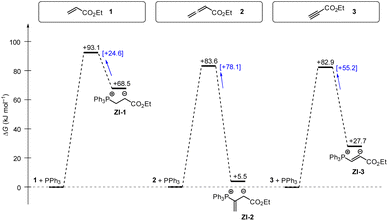 | ||
| Fig. 16 Gibbs energy profiles for PPh3 additions to Michael acceptors 1, 2 and 3 in dichloromethane solution. Experimentally determined Gibbs activation energies ΔG‡exp are combined with quantum-chemically calculated reaction energies ΔGadd (data from Table 4). Reaction barriers for the retro-additions [ΔG‡retro] are given in square brackets. | ||
In the context of multicomponent reactions, such as the Lu reaction (Fig. 17), which starts with a phosphine catalyst in a mixture of competing electrophiles, higher effective concentrations of zwitterionic PR3-allenoate adducts than for the analogous PR3-acrylate adducts may be one of the origins for the chemoselectivity of this cycloaddition.
Tributylphosphine PBu3 is more nucleophilic and Lewis basic than PPh3. At first glance and neglecting the practical challenges associated with handling air-sensitive catalysts, PBu3 might therefore appear to be a generally more effective Lewis base catalyst than PPh3. The reaction profile of PBu3 addition to allenoate 2 in Fig. 18 reveals, however, that the favourable thermodynamics for the zwitterionic adduct formations is linked to a rather large barrier for the heterolytic P–C bond cleavage. In phosphine catalysis this may imply that the final step of the catalytic cycle (e.g. in Fig. 17), that is the release of the PR3 catalyst, may become unfavourably slow. As a consequence, optimisation of reaction conditions regularly requires to keep a delicate balance between formation of a sufficient concentration of PR3 adducts by using highly reactive (nucleophilic) and Lewis basic phosphines and the antagonistic necessity of installing good PR3 nucleofuges that allow for the efficient release of the catalyst in the final step of the catalytic cycle. The combination of experimental and quantum-chemical data to characterise the philicity/fugality features of tertiary phosphines in this work may therefore be helpful to guide future attempts to use phosphine catalysis in organic synthesis.
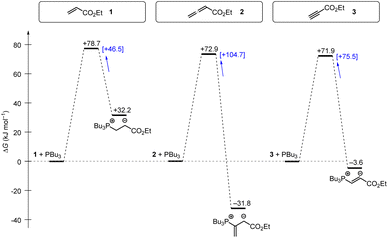 | ||
| Fig. 18 Gibbs energy profiles for PBu3 additions to Michael acceptors 1, 2 and 3 in dichloromethane solution. Experimentally determined Gibbs activation energies ΔG‡exp are combined with quantum-chemically calculated reaction energies ΔGadd (data from Table 4). Reaction barriers for the retro-additions [ΔG‡retro] are given in square brackets. | ||
Not all steps of phosphine-catalysed reactions are well accessible by experiment, e.g. in the Lu reaction. Further quantum-chemical investigations of the full cycle of phosphine-catalysed reactions are, therefore, ongoing to gain further insight in the relevant factors that need to be understood for a systematic improvement of these versatile reactions.
Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
Project conceptualisation and funding acquisition were done jointly by Y. W., M. S., H. Z. and A. R. O. Experimental methodology development and kinetic investigations were carried out by F. A. and supervised by A. R. O. Results of the kinetic measurements were formally analysed and visualised by F. A. and A. R. O. Quantum-chemical investigations, supervised by H. Z., were performed, analysed and visualised by H. J. and J. B. Results were discussed with Y. W. and M. S. The manuscript was written jointly by H. Z., J. B. and A. R. O. with input from all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the Deutsche Forschungsgemeinschaft DFG (project number 410831260) and the National Natural Science Foundation of China (NSFC, project number 21861132014). Jan Brossette is funded by Deutsche Forschungsgemeinschaft (RTG 2620 Ion Pair Effects in Molecular Reactivity, project number 426795949). We gratefully acknowledge generous support for this project through the Leibniz-Rechenzentrum (LRZ) in Munich.References
- (a) L. Horner and K. Klüpfel, Zum Nachweis des polaren Charakters in Doppelbindungs-Systemen Phosphororganische Verbindungen II, Liebigs Ann. Chem., 1955, 591, 69–98 CrossRef CAS; (b) L. Horner, W. Jurgeleit and K. Klüpfel, Zur anionotropen Polymerisationsauslösung bei Olefinen Tertiäre Phosphine III, Liebigs Ann. Chem., 1955, 591, 108–117 CrossRef CAS.
- K.-i. Morita, Z. Suzuki and H. Hirose, A Tertiary Phosphine-catalyzed Reaction of Acrylic Compounds with Aldehydes, Bull. Chem. Soc. Jpn., 1968, 41, 2815 CrossRef CAS.
- D. Basavaiah, B. S. Reddy and S. S. Badsara, Recent Contributions from the Baylis-Hillman Reaction to Organic Chemistry, Chem. Rev., 2010, 110, 5447–5674 CrossRef CAS.
- Y. Wei and M. Shi, Recent Advances in Organocatalytic Asymmetric Morita–Baylis–Hillman/aza-Morita–Baylis–Hillman Reactions, Chem. Rev., 2013, 113, 6659–6690 CrossRef CAS.
- Reviews: (a) X. Lu, C. Zhang and Z. Xu, Reactions of Electron-Deficient Alkynes and Allenes under Phosphine Catalysis, Acc. Chem. Res., 2001, 34, 535–544 CrossRef CAS; (b) L.-W. Ye, J. Zhou and Y. Tang, Phosphine-triggered synthesis of functionalized cyclic compounds, Chem. Soc. Rev., 2008, 37, 1140–1152 RSC; (c) Z. Wang, X. Xu and O. Kwon, Phosphine catalysis of allenes with electrophiles, Chem. Soc. Rev., 2014, 43, 2927–2940 RSC; (d) M. Shi, Y. Wei, M.-X. Zhao and J. Zhang, Organocatalytic Cycloadditions for Synthesis of Carbo- and Heterocycles, Wiley-VCH, Weinheim, 2018 CrossRef; (e) Y. Huang, J. Liao, W. Wang, H. Liu and H. Guo, Synthesis of heterocyclic compounds through nucleophilic phosphine catalysis, Chem. Commun., 2020, 56, 15235–15281 RSC; (f) Y. Wei and M. Shi, Asymmetric Reactions Catalyzed by Chiral Tertiary Phosphines, Chin. J. Chem., 2020, 38, 1395–1421 CrossRef CAS; (g) C. Xie, A. J. Smaligo, X.-R. Song and O. Kwon, Phosphorus-Based Catalysis, ACS Cent. Sci., 2021, 7, 536–558 CrossRef CAS.
- (a) A. V. Salin, A. V. Il’in, F. G. Shamsutdinova, A. R. Fatkhutdinov, D. R. Islamov, O. N. Kataeva and V. I. Galkin, The Pudovik Reaction Catalyzed by Tertiary Phosphines, Curr. Org. Synth., 2013, 13, 132–141 CrossRef; (b) J. T. Maddigan-Wyatt, M. T. Blyth, J. Ametovski, M. L. Coote, J. F. Hooper and D. W. Lupton, Redox Isomerization/(3+2) Allenoate Annulation by Auto-Tandem Phosphine Catalysis, Chem. - Eur. J., 2021, 27, 16232–16236 CrossRef CAS.
- (a) C. Gimbert, M. Lumbierres, C. Marchi, M. Moreno-Mañas, R. M. Sebastián and A. Vallribera, Michael additions catalyzed by phosphines. An overlooked synthetic method, Tetrahedron, 2005, 61, 8598–8605 CrossRef CAS; (b) D. Enders, A. Saint-Dizier, M.-I. Lannou and A. Lenzen, The Phospha-Michael Addition in Organic Synthesis, Eur. J. Org Chem., 2006, 29–49 CrossRef CAS.
- (a) S. E. Denmark and G. L. Beutner, Lewis Base Catalysis in Organic Synthesis, Angew. Chem., Int. Ed., 2008, 47, 1560–1638 CrossRef CAS; (b) S. Lakhdar, Quantitative Treatments of Nucleophilicity and Carbon Lewis Basicity, in Lewis Base Catalysis in Organic Synthesis, ed. E. Vedejs and S. E. Denmark, Wiley-VCH, Weinheim, 1st edn, 2016, pp. 85–118 Search PubMed; (c) H. Guo, Y. C. Fan, Z. Sun, Y. Wu and O. Kwon, Phosphine Organocatalysis, Chem. Rev., 2018, 118, 10049–10293 CrossRef CAS; (d) S. B. Nallapati and S.-C. Chuang, Phosphine-Catalyzed Reactions with Unsaturated Carbonyl Compounds, Asian J. Org. Chem., 2018, 7, 1743–1757 CrossRef CAS; (e) S. Khong, T. Venkatesh and O. Kwon, Nucleophilic Phosphine Catalysis: The Untold Story, Asian J. Org. Chem., 2021, 10, 2699–2708 CrossRef CAS; (f) Y. Meng, L. Chen and E.-Q. Li, Recent Advances in Lewis Base-Catalysed Chemo-, Diastereo- and Enantiodivergent Reactions of Electrondeficient Olefins and Alkynes, Chem. Rec., 2022, 22, e202100276 CrossRef CAS; (g) A. V. Salin and S. A. Shabanov, Advances in organocatalysis of the Michael reaction by tertiary phosphines, Catal. Rev., 2023, 1–90 CrossRef; (h) Q.-F. Li, J. Ma, J. Meng and E.-Q. Li, Recent Advances in Nucleophilic Lewis Base-Catalyzed Cycloadditions for Synthesis of Spirooxindoles, Adv. Synth. Catal., 2023, 365, 4412–4439 CrossRef CAS.
- H. Ni, W.-L. Chan and Y. Lu, Phosphine-Catalyzed Asymmetric Organic Reactions, Chem. Rev., 2018, 118, 9344–9411 CrossRef CAS.
- T. K. Heiss, R. S. Dorn and J. A. Prescher, Bioorthogonal Reactions of Triarylphosphines and Related Analogues, Chem. Rev., 2021, 121, 6802–6849 CrossRef CAS.
- A. V. Salin, A. R. Fatkhutdinov, A. V. Il’in, E. I. Sotov, A. A. Sobanov, V. I. Galkin and B. R. James, Mechanistic aspects of reactions of triphenylphosphine with electron-deficient alkenes in acetic acid solution, J. Phys. Org. Chem., 2013, 26, 675–678 CrossRef CAS.
- A. V. Salin, A. R. Fatkhutdinov, A. V. Il’in, V. I. Galkin and F. G. Shamsutdinova, Solvent Effect on Kinetics and Mechanism of the Phospha-Michael Reaction of Tertiary Phosphines with Unsaturated Carboxylic Acids, Heteroat. Chem., 2014, 25, 205–216 CrossRef CAS.
- A. V. Salin, Mechanistic insights into phospha-Michael reaction of tertiary phosphines with electron-deficient alkenes, Phosphorus, Sulfur Silicon Relat. Elem., 2016, 191, 1625–1627 CrossRef CAS.
- A. V. Salin, A. A. Shabanov, K. R. Khayarov, R. I. Nugmanov and D. R. Islamov, Stereoelectronic Effect in the Reaction of α-Methylene Lactones with Tertiary Phosphines and Its Applications in Organocatalysis, J. Org. Chem., 2023, 88, 11954–11967 CrossRef CAS.
- F. An, H. Jangra, Y. Wei, M. Shi, H. Zipse and A. R. Ofial, Reactivities of allenic and olefinic Michael acceptors towards phosphines, Chem. Commun., 2022, 58, 3358–3361 RSC.
- A reactivity ratio of k(1)/k(2) = 111 was reported for the Michael addition of pyrrolidine (in CHCl3): C. Kiattisewee, A. Kaidad, C. Jiarpinitnun and T. Luanphaisarnnont, Kinetic studies of conjugate addition of amines to allenic and acrylic esters and their correlation with antibacterial activities against Staphylococcus aureus, Monatsh. Chem., 2018, 149, 1059–1068 CrossRef CAS.
- H. Hoffmann, Zur Reaktion von Triphenylphosphin mit Olefinen, Chem. Ber., 1961, 94, 1331–1336 CrossRef CAS.
- The alkylation of PPh3 by methyl acrylate in the presence of triflic acid was described in: B. Patzke and R. Sustmann, Dimerization of methyl acrylate by homogeneous transition metal catalysis. Part II. Activation of dihydridoruthenium(II)phosphane complexes by CF3SO3H, J. Organomet. Chem., 1994, 480, 65–74 CrossRef CAS.
- H. Ohmori, T. Takanami, H. Shimada and M. Masui, Simple Preparation of 3-Oxoalkyltriphenylphosphonium Salts Effected by Using 2,6-Lutidinium Salts, Chem. Pharm. Bull., 1987, 35, 2558–2560 CrossRef CAS.
- S. Tshepelevitsh, A. Kütt, M. Lõkov, I. Kaljurand, J. Saame, A. Heering, P. G. Plieger, R. Vianello and I. Leito, On the Basicity of Organic Bases in Different Media, Eur. J. Org Chem., 2019, 2019, 6735–6748 CrossRef CAS.
- M. S. Robinson, M. L. Polak, V. M. Bierbaum, C. H. DePuy and W. C. Lineberger, Experimental Studies of Allene, Methylacetylene, and the Propargyl Radical: Bond Dissociation Energies, Gas-Phase Acidities, and Ion–Molecule Chemistry, J. Am. Chem. Soc., 1995, 117, 6766–6778 CrossRef CAS.
- Y. Ben-Tal, P. J. Boaler, H. J. A. Dale, R. E. Dooley, N. A. Fohn, Y. Gao, A. García-Domínguez, K. M. Grant, A. M. R. Hall, H. L. D. Hayes, M. M. Kucharski, R. Wei and G. C. Lloyd-Jones, Mechanistic analysis by NMR spectroscopy: A users guide, Prog. Nucl. Magn. Reson., 2022, 129, 28–106 CrossRef CAS.
- T. Lemek and H. Mayr, Electrophilicity Parameters for Benzylidenemalononitriles, J. Org. Chem., 2003, 68, 6880–6886 CrossRef CAS.
- X. Lu, Z. Lu and X. Zhang, Phosphine-catalyzed one-pot synthesis of cyclopentenes from electron-deficient allene, malononitrile and aromatic aldehydes, Tetrahedron, 2006, 62, 457–460 CrossRef CAS.
- Y. Liang, S. Liu, Y. Xia, Y. Li and Z.-X. Yu, Mechanism, Regioselectivity, and the Kinetics of Phosphine-Catalyzed [3+2] Cycloaddition Reactions of Allenoates and Electron-Deficient Alkenes, Chem. - Eur. J., 2008, 14, 4361–4373 CrossRef CAS.
- Q. Chen, P. Mayer and H. Mayr, Ethenesulfonyl Fluoride: The Most Perfect Michael Acceptor Ever Found?, Angew. Chem., Int. Ed., 2016, 55, 12664–12667 CrossRef CAS.
- Reactivities of further, sterically demanding PR3 were studied in: E. Follet, P. Mayer, D. S. Stephenson, A. R. Ofial and G. Berionni, Reactivity-Tuning in Frustrated Lewis Pairs: Nucleophilicity and Lewis Basicity of Sterically Hindered Phosphines, Chem. - Eur. J., 2017, 23, 7422–7427 CrossRef CAS.
- (a) F. G. Bordwell, J. C. Branca and T. A. Cripe, Brønsted βNu Values and Leaving Group Effects in SN2 Reactions. Tests of the Reactivity—Selectivity Postulate, Isr. J. Chem., 1985, 26, 357–366 CrossRef CAS; (b) H. Mayr and A. R. Ofial, The Reactivity-Selectivity Principle: An Imperishable Myth in Organic Chemistry, Angew. Chem., Int. Ed., 2006, 45, 1844–1854 CrossRef CAS.
- (a) W. A. Henderson Jr and C. A. Streuli, The Basicity of Phosphines, J. Am. Chem. Soc., 1960, 82, 5791–5794 CrossRef; (b) W. A. Henderson Jr and S. A. Buckler, The Nucleophilicity of Phosphines, J. Am. Chem. Soc., 1960, 82, 5794–5800 CrossRef.
- (a) T. Allman and R. G. Goel, The basicity of phosphines, Can. J. Chem., 1982, 60, 716–722 CrossRef CAS; (b) P. M. Zizelman, C. Amatore and J. K. Kochi, Steric and Electronic Effects in Ligand Substitution of Metal Carbonyls. Rapid Kinetics of Labile Carbonylmanganese Complexes by Transient Electrochemical Techniques, J. Am. Chem. Soc., 1984, 106, 3771–3784 CrossRef CAS.
- L. A. P. Kane-Maguire, E. D. Honig and D. A. Sweigart, Nucleophilic addition to coordinated cyclic π-hydrocarbons: mechanistic and synthetic studies, Chem. Rev., 1984, 84, 525–543 CrossRef CAS.
- N. P. Taylor, J. A. Gonzalez, G. S. Nichol, A. García-Domínguez, A. G. Leach and G. C. Lloyd-Jones, A Lewis Base Nucleofugality Parameter, NFB, and its Application in an Analysis of MIDA-boronate Hydrolysis Kinetics, J. Org. Chem., 2022, 87, 721–729 CrossRef CAS.
- T. Kanzian, T. A. Nigst, A. Maier, S. Pichl and H. Mayr, Nucleophilic Reactivities of Primary and Secondary Amines in Acetontrile, Eur. J. Org Chem., 2009, 6379–6385 CrossRef CAS.
- J. Ammer, M. Baidya, S. Kobayashi and H. Mayr, Nucleophilic reactivities of tertiary alkylamines, J. Phys. Org. Chem., 2010, 23, 1029–1035 CrossRef CAS.
- J. P. Richard, M. M. Toteva and J. Crugeiras, Structure−Reactivity Relationships and Intrinsic Reaction Barriers for Nucleophile Additions to a Quinone Methide: A Strongly Resonance-Stabilized Carbocation, J. Am. Chem. Soc., 2000, 122, 1664–1674 CrossRef CAS.
- T. B. Phan, M. Breugst and H. Mayr, Towards a General Scale of Nucleophilicity?, Angew. Chem., Int. Ed., 2006, 45, 3869–3874 CrossRef CAS.
- R. J. Mayer, T. Tokuyasu, P. Mayer, J. Gomar, S. Sabelle, B. Mennucci, H. Mayr and A. R. Ofial, Solvation Accounts for the Counter-Intuitive Nucleophilicity Ordering of Peroxide Anions, Angew. Chem., Int. Ed., 2017, 56, 13279–13282 CrossRef CAS.
- J. G. Atton and L. A. P. Kane-Maguire, Kinetics of nucleophilic attack on co-ordinated organic moieties. Part 21. Factors governing the nucleophilicity of phosphorus nucleophiles towards [Fe(CO)3(1–5-η-C6H7)]+, J. Chem. Soc., Dalton Trans., 1982, 1491–1498 RSC.
- H. Mayr and A. R. Ofial, Philicity, fugality, and equilibrium constants: when do rate-equilibrium relationships break down?, Pure Appl. Chem., 2017, 89, 729–744 CrossRef CAS ; and refs cited therein..
- M. Baidya, S. Kobayashi, F. Brotzel, U. Schmidhammer, E. Riedle and H. Mayr, DABCO or DMAP – Why Are They Different in Organocatalysis?, Angew. Chem., Int. Ed., 2007, 46, 6476–6479 CrossRef.
- H. Mayr, S. Lakhdar, B. Maji and A. R. Ofial, A quantitative approach to nucleophilic organocatalysis, Beilstein J. Org. Chem., 2012, 8, 1458–1478 CrossRef CAS.
- B. Maji, X.-H. Duan, P. M. Jüstel, P. A. Byrne, A. R. Ofial and H. Mayr, Nucleophilicities and Nucleofugalities of Thio- and Selenoethers, Chem. - Eur. J., 2021, 27, 11367–11376 CrossRef CAS.
- (a) R. A. Marcus, Theoretical relations among rate constants, barriers, and Broensted slopes of chemical reactions, J. Phys. Chem., 1968, 72, 891–899 CrossRef CAS; (b) R. A. Marcus, Unusual slopes of free energy plots in kinetics, J. Am. Chem. Soc., 1969, 91, 7224–7225 CrossRef CAS; (c) W. J. Albery, The Application of the Marcus Relation to Reactions in Solution, Annu. Rev. Phys. Chem., 1980, 31, 227–263 CrossRef CAS.
- B. Maji, M. Baidya, J. Ammer, S. Kobayashi, P. Mayer, A. R. Ofial and H. Mayr, Nucleophilic Reactivities and Lewis Basicities of 2-Imidazolines and Related N-Heterocyclic Compounds, Eur. J. Org Chem., 2013, 3369–3377 CrossRef CAS.
- (a) Y. Xia, Y. Liang, Y. Chen, M. Wang, L. Jiao, F. Huang, S. Liu, Y. Li and Z. X. Yu, An Unexpected Role of a Trace Amount of Water in Catalyzing Proton Transfer in Phosphine-Catalyzed (3+2) Cycloaddition of Allenoates and Alkenes, J. Am. Chem. Soc., 2007, 129, 3470–3471 CrossRef CAS; (b) E. Mercier, B. Fonovic, C. Henry, O. Kwon and T. Dudding, Phophine triggered [3+2] allenoate-acrylate annulation: a mechanistic enlightenment, Tetrahedron Lett., 2007, 48, 3617–3620 CrossRef CAS.
- (a) H. S. Yu, X. He, S. L. Li and D. G. Truhlar, MN15: A Kohn–Sham global-hybrid exchange–correlation density functional with broad accuracy for multi-reference and single-reference systems and noncovalent interactions, Chem. Sci., 2016, 7, 5032–5051 ( Chem. Sci. , 2016 , 7 , 6278–6279 ) RSC; (b) F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC; (c) A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS.
- D. Kadish, A. D. Mood, M. Tavakoli, E. S. Gutman, P. Baldi and D. L. Van Vranken, Methyl Cation Affinities of Canonical Organic Functional Groups, J. Org. Chem., 2021, 86, 3721–3729 CrossRef.
- For MCAs of PR3 in the gas phase, see: C. Lindner, R. Tandon, B. Maryasin, E. Larionov and H. Zipse, Phosphine-Catalyzed Asymmetric Organic Reactions, Beilstein J. Org. Chem., 2012, 8, 1406–1442 CrossRef CAS.
- J. Hine and R. D. Weimar Jr, Carbon Basicity, J. Am. Chem. Soc., 1965, 87, 3387–3396 CrossRef CAS.
- A. Bondi, van der Waals Volumes and Radii, J. Phys. Chem., 1964, 68, 441–451 CrossRef CAS.
- (a) F. M. Bickelhaupt and K. N. Houk, Analyzing Reaction Rates with the Distortion/Interaction-Activation Strain Model, Angew. Chem., Int. Ed., 2017, 56, 10070–10086 CrossRef CAS; (b) P. Vermeeren, S. C. C. van der Lubbe, C. Fonseca Guerra, F. M. Bickelhaupt and T. A. Hamlin, Understanding chemical reactivity using the activation strain model, Nat. Protoc., 2020, 15, 649–667 CrossRef CAS; (c) P. Vermeeren, T. A. Hamlin and F. M. Bickelhaupt, Chemical reactivity from an activation strain perspective, Chem. Commun., 2021, 57, 5880–5896 RSC.
Footnotes |
| † Electronic supplementary information (ESI) available: Additional figures, details of synthetic procedures, analytics and product characterisation, kinetic measurements, quantum-chemical calculations and geometries of optimised structures. See DOI: https://doi.org/10.1039/d4sc04852k |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |