Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Single molecules of terrylene in di-substituted naphthalenes crystallizing in the herringbone pattern†
Magda Białkowska a,
Wojciech Chaładaj
a,
Wojciech Chaładaj b,
Irena Deperasińska
b,
Irena Deperasińska a,
Aleksandra Drzewiecka-Antonik
a,
Aleksandra Drzewiecka-Antonik a,
Anna E. Koziol
a,
Anna E. Koziol c,
Artur Makarewicz
c,
Artur Makarewicz a and
Bolesław Kozankiewicz
a and
Bolesław Kozankiewicz *a
*a
aInstitute of Physics, Polish Academy of Sciences, Al. Lotników 32/46, 02-668 Warsaw, Poland. E-mail: kozank@ifpan.edu.pl
bInstitute of Organic Chemistry, Polish Academy of Sciences, Kasprzaka 44/52, 01-224 Warsaw, Poland
cFaculty of Chemistry, Maria Curie-Skłodowska University, 20-031 Lublin, Poland
First published on 16th January 2017
Abstract
2,3-Dichloronaphthalene (2,3-DCN) and 2,3-dibromonaphthalene (2,3-DBN) were synthesized, purified and used to grow single crystals in the form of thin plates. X-ray crystallographic studies, performed for the first time, showed that molecules in both isostructural crystals are arranged in the herringbone pattern. These crystals, lightly doped with terrylene (Tr), appeared to be very good systems for optical single-molecule studies. Fluorescence excitation spectra of single Tr molecules at 5 K in excess of the dominating purely electronic (0, 0) and intense vibronic line of ∼250 cm−1 frequency had a new, “184 cm−1” line, absent in the spectrum of isolated (D2h) Tr. Quantum-chemistry calculations indicated that this new line was the fingerprint of the deformation of the Tr molecule in the crystal structure, which lowered its symmetry to C2h.
Introduction
Optical detection of single molecules, more than 25 years after the first reports,1,2 found multiple applications in a wide range of fields like material science, quantum optics and biophysics.3,4 The main advantage of the single-molecule research is that it removes ensemble-averaging and opens the door to study the properties of the nano-world. Experiments are however difficult and only a few molecule/matrix systems can be used for such an optical study.First of all a molecule for single-molecule optical research has to be a very efficient emitter of fluorescence photons. This means a high absorption cross section for population of the lowest excited singlet S1 state and high fluorescence quantum yield for the back, S1 → S0 transition with negligible intersystem crossing to the long-lived triplet T1 state.5 Another important requirement is that the molecule has to avoid photo-bleaching (irreversible photo-reaction), at least for the time sufficient to distinguish the fluorescence photons from the background signal of a detector. As a rule molecules are more stable in rigid environments, especially if the bleaching is due to photo-oxidation. From this point of view convenient choice are solid media, like molecular crystals where dopants occupy well defined incorporation sites and experiments can be performed in a broad temperature range, like in a case of terrylene (Tr) in a p-terphenyl (p-T) crystal.6,7
In order to improve the signal-to-background ratio the illuminated volume of a sample has to be as small as possible. In addition to the use of a microscope objective, which focuses the light to the diffraction limited spot, this requirement prefers the use of a host crystal which can be obtained in a form of thin plate. It is a case of linear aromatic polyacenes which crystallize in the ‘herringbone’ pattern. It is also a case of 2,3-dimethylnaphthalene (2,3-DMN) crystal, which we already used as a solid matrix to study single molecules of Tr.8 2,3-DMN crystallizes in a perfectly ordered lattice, similar to that of anthracene, but with ‘dipolar’ disorder of the constituting molecules.9 This disorder is manifested by broad (fwhm ≈ 120 cm−1 at 5 K) inhomogeneous (0, 0) line in the fluorescence excitation spectrum of an ensemble of Tr molecules.10 The success of using 2,3-DMN as a transparent solid matrix for the single-molecule studies encouraged us to extend investigations on single crystals of 2,3-dichloronaphthalene (2,3-DCN) and 2,3-dibromonaphthalene (2,3-DBN). We expected that these compounds will also crystallize in the herringbone pattern.
In the present work 2,3-DCN and 2,3-DBN were synthesized, extensively purified and used to grow by sublimation the good quality single crystals in the form of thin plates. To our surprise the structures of 2,3-DCN and 2,3-DBN crystals were not known (or at least not published) and therefore the X-ray crystallography was used for their determination. Next, we grew single crystals of 2,3-DCN and 2,3-DBN lightly doped with Tr by using the technique of co-sublimation of both components. These crystals were used for single-molecule optical studies, by a confocal fluorescence microscopy technique at 5 K with a low-resolution laser excitation. The preliminary results of the research were already published.11
In the work we concentrated on deformations of the molecular structure of the guest, Tr, which were induced by the host matrix. This information could be deduced from the structure of fluorescence excitation spectrum recorded at low temperature. Appearance of the new vibronic components, which were absent in the planar form of Tr (D2h symmetry) indicated deformations lowering the molecular symmetry. Analysis of the spectra was performed with the aid of quantum-chemistry calculations.
Results and discussion
Synthesis of 2,3-DCN and 2,3-DBN
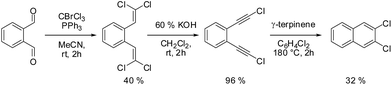
2,3-DCN was obtained from o-phthalaldehyde in three steps according to Scheme 1. More details about the synthesis and the intermediate products are given in the ESI.† Similar three step strategy was utilized to synthesize 2,3-DBN. The final products (2,3-DCN and 2,3-DBN) were obtained in the form of white crystals.X-ray structure analysis of 2,3-DCN and 2,3-DBN single crystals
Single crystals of 2,3-DCN and 2,3-DBN were grown, from zone-refined material, by sublimation under ∼0.2 bar of argon gas atmosphere. The crystals, obtained in the form of thin plates, were investigated by using the X-ray diffraction technique. The crystallographic data, details of data collection and refinement are collected in Table 1.| Compound | 2,3-DCN | 2,3-DBN |
| Formula | C10H6Cl2 | C10H6Br2 |
| Formula weight | 197.05 | 285.97 |
| Crystal system | Orthorhombic | Orthorhombic |
| Space group | Pbca | Pbca |
| a [Å] | 11.631(3) | 11.692(3) |
| b [Å] | 7.417(2) | 7.545(3) |
| c [Å] | 19.691(4) | 20.193(5) |
| V [Å3] | 1698.7(7) | 1781.3(10) |
| Z | 8 | 8 |
| d [g cm−3] | 1.541 | 2.133 |
| F(000) | 800 | 1088 |
| θ range for data collection [°] | 4.49–74.04 | 4.38–75.17 |
| Index ranges | −14 ≤ h ≤ 14 | −14 ≤ h ≤ 13 |
| −6 ≤ k ≤ 8 | −9 ≤ k ≤ 9 | |
| −22 ≤ l ≤ 24 | −24 ≤ l ≤ 16 | |
| Reflections collected/unique/observed [I > 2σ(I)] | 3238/1589/1160 | 6251/1777/1357 |
| Goodness of fit on F2 | 1.089 | 1.004 |
| R1[I > 2σ(I)] | 0.0788 | 0.0475 |
| wR2[I > 2σ(I)] | 0.2002 | 0.12 |
| Residual electron density (max; min) [e Å−3] | 0.48; −0.71 | 0.98; −1.44 |
Molecules of both compounds, 2,3-DCN and 2,3-DBN, appeared to be planar in the crystal structure. The bond lengths and valence angles of the aromatic rings are within the expected ranges and their geometries are analogous to those found in literature.12 The C–Cl and C–Br bond lengths of 2,3-DCN and 2,3-DBN molecules are similar to those observed in their isomers.13
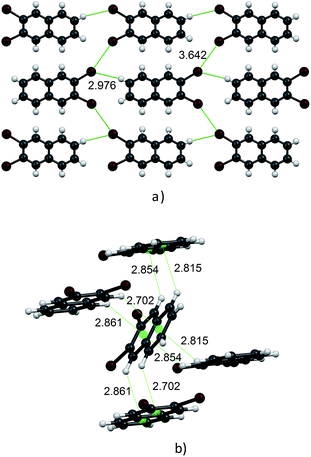
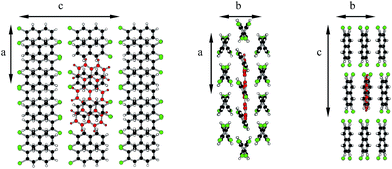
Molecules in the isostructural crystals are held together by weak C–H⋯π, C–H⋯halogen and halogen⋯halogen intermolecular interactions (e.g. Fig. 1 and S2 and Table S1 of the ESI†). The C–H⋯Cl/Br contacts generate chains of molecules along the c-axis. These head-to-tail chains are linked by Cl⋯Cl/Br⋯Br interactions to form a sheet in the ac plane (Fig. 1a). Each of the molecules within the sheet contacts with four neighbor molecules via C–H⋯π bonds (Fig. 1b). All these weak and directional forces play an important role in stabilizing the supramolecular architecture and the herringbone packing of the molecules is observed in both crystals, as shown in Fig. 2. The detailed data describing the crystal structures are available elsewhere.14 Let us mention here, that the crystal lattices of both compounds are ordered, without the statistical disorder of the atomic positions like that observed in 2,3-DMN crystal.9
 | ||
| Fig. 2 Crystal packing viewed down the c-axis: 2,3-DCN – top and 2,3-DBN – bottom. Cl atoms green; Br atoms dark red. | ||
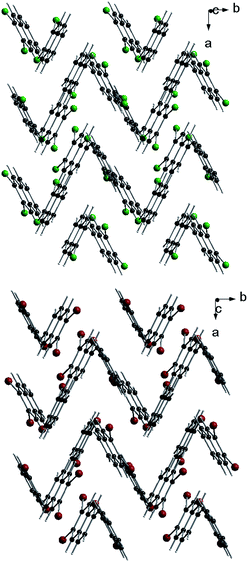
Up to our best knowledge (and to surprise) the present work is the first report of the structures of 2,3-DCN and 2,3-DBN crystals. The only one previously reported crystal structure of the 2,3-dihalogen substituted naphthalene, viz. 2,3-diiodonaphthalene, was published by Novak.15 Structural studies of several other isomers of dibromo- and dichloro-naphthalenes revealed that they do not form the herringbone arrangement. These compounds are: 1,4-dibromo-, 1,5-dibromo-, 1,8-dibromo-, 2,6-dibromo-, 1,4-dichloro- and 2,6-dichloro-naphthalenes.13
Optical studies of single molecules of Tr in 2,3-DCN and 2,3-DBN crystals
Typical fluorescence excitation spectra for a single Tr molecule in a 2,3-DCN crystal, which were obtained when we focused the laser light on a bright spot in the fluorescence excitation image and scanned the excitation frequency within the tuning range of our laser (operating with Rh6G), for the three indicated excitation intensities, were shown in Fig. 3. The spectra composed of the purely electronic (0, 0) line (with the maximum for the investigated molecule located at 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 250 cm−1) and two vibronic lines shifted 184 and 247 cm−1 to higher energy. In the spectrum recorded under high excitation intensity (720 kW cm−2), when the zero-phonon lines were close to saturation, we observed growth of the broad phonon-side band.10,16 Distributions of the energetic position of the (0, 0) lines and of the vibronic frequencies monitored for some other Tr molecules in the investigated crystals can be found in the ESI.† The vibronic line “184 cm−1” has not been observed in previously reported spectra of single Tr molecules embedded in p-T, naphthalene and 2,3-DMN crystals.10,16
250 cm−1) and two vibronic lines shifted 184 and 247 cm−1 to higher energy. In the spectrum recorded under high excitation intensity (720 kW cm−2), when the zero-phonon lines were close to saturation, we observed growth of the broad phonon-side band.10,16 Distributions of the energetic position of the (0, 0) lines and of the vibronic frequencies monitored for some other Tr molecules in the investigated crystals can be found in the ESI.† The vibronic line “184 cm−1” has not been observed in previously reported spectra of single Tr molecules embedded in p-T, naphthalene and 2,3-DMN crystals.10,16
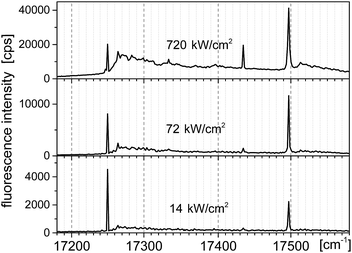 | ||
| Fig. 3 Fluorescence excitation spectra of a typical single molecule of Tr in a 2,3-DCN crystal at 5 K, recorded with the laser excitation intensities given above each spectrum. | ||
Relative intensities of the three fluorescence excitation lines behaved differently with the rise of the laser excitation power (I). The fluorescence intensities in the maximum of the lines, R(I), were plotted in Fig. 4. Fits to the experimental points were done according to the well-known saturation formula:17 R(I) = R∞ × (I/Is)/(1 + (I/Is)), where R∞ is the fully saturated detection rate and Is – the saturation intensity. The fully saturated detection rate R∞ for the excitation to both vibronic states were, within the experimental error, approximately two times higher than that for excitation to the purely electronic state. This is typical observation for Tr molecules, as already reported for other matrices.10,16 Such a behavior is possible if the triplet T1 state population rate constant is considerably smaller than the depopulation rate of this state.16 Then, under the purely electronic excitation populations of the electronic ground S0 and lowest excited S1 states can only reach equal values (1/2 in each state), whereas under excitation to vibronic component population can be completely transferred from the S0 to S1 state. The saturation intensity Is is inversely proportional to the absorption cross section of the considered transition. Analysis of this value is however difficult because Is depends also on the relative widths of absorption and excitation lines. We should remind here, that in the experiment we used a laser with the line-width ∼1 cm−1, approximately 3 orders of magnitude broader than the homogeneous width of the purely electronic excitation line but similar to the widths of the vibronic lines. Thus, we had to use much higher laser intensities than in a typical experiment with a single-mode laser.
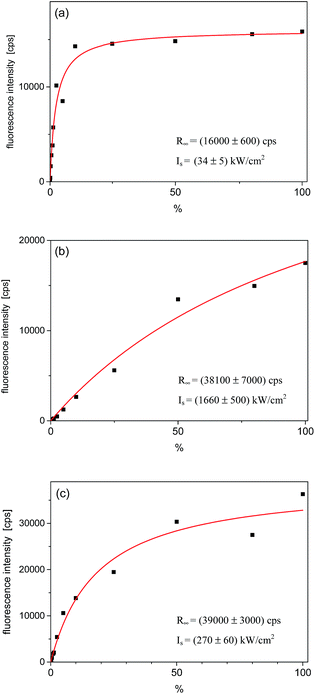 | ||
| Fig. 4 Saturation curves for the single Tr molecule which spectra are shown in Fig. 3. (a) Fluorescence intensity in the maximum of the purely electronic (0, 0) line; (b) for the vibronic 184 cm−1 line, and (c) for the vibronic 247 cm−1 line. The power density scale is given in % of the maximum available power, which was ∼1450 kW cm−2. The fitting parameters are given in corners of each figure. | ||
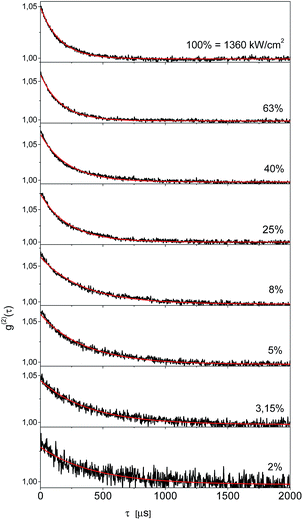
In order to get independent information about the triplet population and depopulation rate constants we measured second order fluorescence intensity correlation function g(2)(τ) for six single Tr molecules in a 2,3-DCN crystal at 5 K. A set of such functions for the same single Tr molecule obtained at several different exciting light intensities was shown in Fig. 5. The characteristic feature, observed for other Tr molecules in this matrix as well, was pretty good fit to a single exponential decay dependence. It might indicate either extremely weak population of the long-lived triplet state spin sublevel, and/or fast spin-lattice relaxation equalizing population of the spin sublevels already at 5 K.18 Using the procedure described in our previous article,19 we estimated for the molecule contributing to the decays presented in Fig. 4 that the triplet state population rate constant k23 = 800 ± 70 s−1, whereas the rate constant of depopulation of this state kT = 2500 ± 200 s−1. For five other single Tr molecules investigated in this crystal the estimated rate constants k23 were between 700 and 1300 s−1, and the rate constants kT between 1800 and 3600 s−1. For each Tr molecule the kT value was always 2–3 times bigger than that for k23, in agreement with the conclusion derived from the analysis of the fluorescence intensity saturation dependence. Both rate constants were subject of increase with the rise of temperature, but within the whole available temperature range, from 5 to 300 K, we were able to detect single molecules of Tr.11 By the same, external heavy-atom effect on the dopants, Tr molecules, connected with the chlorine atoms in the crystalline 2,3-DCN, was weak and did not quenched efficiently their fluorescence. We rationalized such a situation in terms of the energy diagram of the electronic states of Tr, which prevents efficient spin–orbit coupling between the singlet S1 and the triplet T1 and T2 states responsible for the intersystem crossing pathway.11,20 The bright and photostable single molecules of Tr were already detected in polycrystalline 1,2-21 and 1,4-dichlorobenzenes,22 both host matrices with heavy-atoms of chlorine.
The (0, 0) fluorescence line of a bulk sample of Tr in a 2,3-DBN crystal was slightly shifted to higher energy as compare with that in 2,3-DCN crystal. The (0, 0) line onset was at 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 cm−1 and the line maximum at 17
300 cm−1 and the line maximum at 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 260 cm−1 (see Fig. S5 in the ESI†). Fluorescence decays of a bulk sample were well fitted to mono-exponential dependence with the average decay time of about 3.6 ns, not much different from that for Tr in several solids lacking heavy-atoms.23 Such a result suggested that the presence of the bromide heavy-atoms in the crystal, which might lead to an increase of the intersystem crossing yield, did not disturb significantly the total depopulation yield of the singlet S1 state. We succeeded to detect several single molecules of Tr in a 2,3-DBN crystal which had their purely electronic (0, 0) lines located between 17
260 cm−1 (see Fig. S5 in the ESI†). Fluorescence decays of a bulk sample were well fitted to mono-exponential dependence with the average decay time of about 3.6 ns, not much different from that for Tr in several solids lacking heavy-atoms.23 Such a result suggested that the presence of the bromide heavy-atoms in the crystal, which might lead to an increase of the intersystem crossing yield, did not disturb significantly the total depopulation yield of the singlet S1 state. We succeeded to detect several single molecules of Tr in a 2,3-DBN crystal which had their purely electronic (0, 0) lines located between 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 283 and 17
283 and 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 290 cm−1. Experiments appeared however more difficult than those with 2,3-DCN crystal because of lower photostability of Tr molecules in 2,3-DBN crystal. We were not lucky to find any single Tr molecule photo-stable enough to collect a set of fluorescence excitation spectra as well as a set of fluorescence intensity autocorrelation functions at sufficiently high excitation laser powers required for convincing estimation of the triplet T1 state population rate constant. From the analysis of the fluorescence intensity correlation function, collected with the low intensity of exciting light, we were only able to estimate the population rate constant kT. It was between 30
290 cm−1. Experiments appeared however more difficult than those with 2,3-DCN crystal because of lower photostability of Tr molecules in 2,3-DBN crystal. We were not lucky to find any single Tr molecule photo-stable enough to collect a set of fluorescence excitation spectra as well as a set of fluorescence intensity autocorrelation functions at sufficiently high excitation laser powers required for convincing estimation of the triplet T1 state population rate constant. From the analysis of the fluorescence intensity correlation function, collected with the low intensity of exciting light, we were only able to estimate the population rate constant kT. It was between 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 55
000 and 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 s−1, an order of magnitude bigger than for Tr molecules in a 2,3-DCN crystal. The other behavior observed for Tr molecules in 2,3-DBN crystal was moreover the same as that in 2,3-DCN crystal, although the vibronic frequencies were slightly bigger (see Fig. S4 in the ESI†).
000 s−1, an order of magnitude bigger than for Tr molecules in a 2,3-DCN crystal. The other behavior observed for Tr molecules in 2,3-DBN crystal was moreover the same as that in 2,3-DCN crystal, although the vibronic frequencies were slightly bigger (see Fig. S4 in the ESI†).
Quantum-chemistry calculations
Electronic states and spectra of Tr molecules were already subject of several quantum-chemistry studies.24–29 In the present work we complemented our previous DFT B3LYP/6-31g(d,p) calculations performed for Tr in the ground S0 state with the calculations for the excited S1 state performed by TD DFT B3LYP/6-31g(d,p). Details of Tr geometry and vibrational frequencies in both states for isolated Tr were given in the ESI (Tables S2 and S3†).The lowest energy purely electronic S0 → S1 transition is of the Ag → B1u symmetry (in the convention that long axis is Z, short Y and axis Z is perpendicular to the molecule plane). It is strongly allowed and polarized along the long axis of Tr. Calculated vibronic structure of fluorescence excitation spectrum for isolated, planar Tr molecule (D2h symmetry) was presented in Fig. 6. Vibronic excitation spectrum composed of ag vibrations and in the low energy range (up to 300 cm−1 above the (0, 0) line) there was only single line of the 247 cm−1 frequency. Such a spectrum, composed of (0, 0) and ∼250 cm−1 vibronic lines, was observed by us for single molecules of Tr dispersed in p-T16 and 2,3-DMN crystals.10 It was however not a case of Tr molecules in 2,3-DCN crystal investigated in this work, because in the fluorescence excitation spectrum in excess of the vibronic 247 cm−1 line we observed an extra vibronic line separated from the purely electronic (0, 0) origin by 184 cm−1.
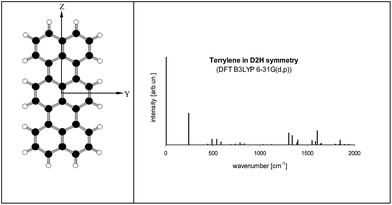 | ||
Fig. 6 (left) Structure of Tr molecule with the coordinate axes used in this work (X axis perpendicular to YZ plane). (right) Calculated fluorescence excitation spectrum of Tr (D2h symmetry). S0 state was optimized by DFT B3LYP/6-31G(d,p) method, S1 state optimized by TD DFT B3LYP/6-31G(d,p) method. Details about the geometry, vibronic frequencies and Franck–Condon factors were given in Tables S2–S4 of the ESI.† Calculated energy of the (0, 0) transition (with the correction for the zero-point energy) was 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 547 cm−1. 547 cm−1. | ||
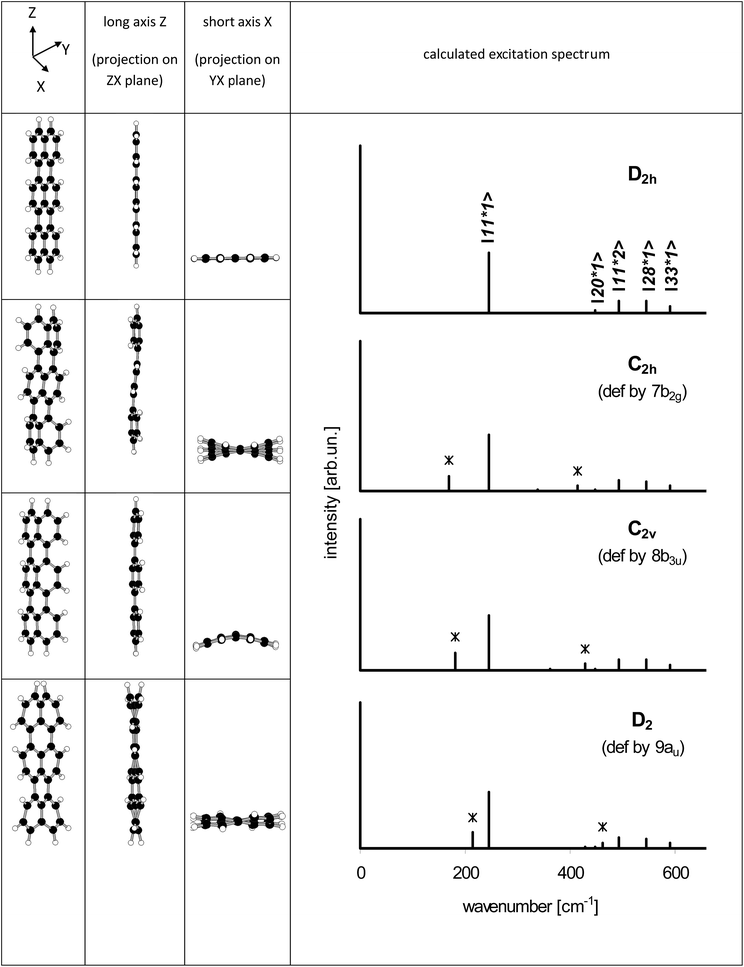
From the point of view of the symmetry selection rules appearance of the additional lines visualizes lowering of the symmetry of the investigated molecule, for example due to interaction with the surrounding host molecules. According to our calculations (see Table S4 of the ESI†) in the low frequency range, close to 184 cm−1, there were three vibrations: 7b2g, 8b3u and 9au, which frequencies in the S1 state were 174, 181 and 206 cm−1, respectively. All of them were out-of-plane vibrations and were inactive in the S0 → S1 transition for planar Tr. Franck–Condon principle predicts that the vibronic line should appear in the S0 → S1 spectrum if the projection of the geometry change between the initial and final states onto the normal modes of the final states follows displacement vectors of the vibration.30 A good example is ∼247 cm−1 (ag) vibration in isolated Tr, in which the displacement vectors point along the long axis of the molecule,27,29 and the transition between the electronic S0 and S1 states is connected with the shortening of the bond lengths between the central and the external naphthalene moieties25 (see the structures presented in Table S5 of the ESI†).
Such a practical application of the Franck–Condon rule was used by us to model the vibronic spectra of Tr where the symmetry of molecule was lowered in the controllable way. We used the Y and Z coordinates of Tr atoms like those calculated for planar D2h molecule, whereas the X (out-of-plane) coordinates in the ground S0 state were deformed proportionally to the displacement vectors of the 7b2g, 8b3u and 9au vibrations. In the model, we assumed that deformation in the X direction of the excited Tr was much smaller than in the ground S0 state. It has been known25 (see Table S5 of the ESI†) that Tr molecule after excitation to the S1 state shortens length of its long axis and decreases the molecular volume from 3122.6 bohr3 per mole to 2914.1 bohr3 per mole. Tr molecule in the excited state has a little more space in the occupied cavity and thus may have more planar structure.25,26,28 Therefore, for the deformed Tr molecules in the S1 state we used coordinates almost identical (up to the fourth decimal place) as those for planar (D2h) Tr. With the new coordinates (see Table S6 of the ESI†) the molecular symmetry was lowered to C2h, C2v and D2, respectively. Projections of the deformed structures of Tr molecule on the different molecular planes were shown on the left side of Fig. 7. The characteristic feature of “7b2g” deformation was out-of-plane tilting of the long axis of Tr where the external naphthalene moieties moved in the opposite directions resembling the shape of letter “S”. Linearity of the long axis of molecule was preserved in two other, “8b3u” and “9au” deformations. All the calculated frequencies of the vibrations of Tr molecule deformed these ways were positive and were collected in Table S7 of the ESI.† Basing only on the symmetry rules we might expect appearance of the new lines corresponding to vibrations 4 and 7 for Tr deformed to C2h symmetry, vibrations 3, 5 and 8 for Tr in C2v symmetry, and vibrations 1 and 9 for Tr in D2 symmetry. However, taking into account the Franck–Condon factors the number of vibronic lines of the sufficiently high intensity was reduced. Calculated vibronic spectra of the deformed Tr molecules were plotted at the right side of Fig. 7, whereas the numerical data were collected in Table S8 of the ESI.† In Fig. 7, the new lines which were absent for planar Tr were marked by *. Each spectrum of the deformed Tr had characteristic additional line (next to the ag 247 cm−1 line) and lesser intensity line, which was combination of the vibration ag with the characteristic vibration.
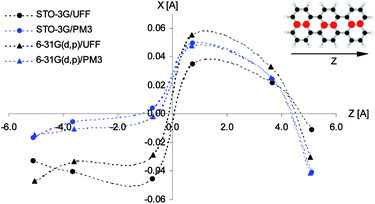
The distinct deformations of the Tr geometry which were manifested in appearance of the new, closely in frequency lying vibronic lines tended us to investigate possible deformations in the crystalline environment. Calculations were performed with the aid of ONIOM procedure included in the Gaussian 09 package. We assumed that a guest Tr molecule replaced in the crystal structure three host molecules. For calculation of Tr structure we used the high level of ONIOM, for calculation of host crystal structure the low level of ONIOM. We considered different insertion sites and the lowest energy configuration was presented in Fig. 8. The long Tr axis in this site is nearly parallel to the axis a of the crystal (more precisely the angles between both axes were 5.8 and 9 degree in 2,3-DCN and 2,3-DBN crystals, respectively), whereas the short axis of Tr is nearly parallel to the axis c of the crystal (more precisely, the angles between both axes were 2 and 5 degree in 2,3-DCN and 2,3-DBN crystals, respectively). Energies of the (0, 0) transitions and frequencies of the “ag” and “b2g” vibrations calculated with the aid of different methods were collected in Table S10 of the ESI.†
According to calculations Tr in 2,3-DCN and 2,3-DBN crystals was not a planar molecule (calculated coordinates were given in Table S9 of the ESI†), nor a symmetric one. Lack of the symmetry was caused by the surrounding host molecules which differently interact with different moieties of the guest molecule. To characterize the deformation in Fig. 9 we plotted calculated bending of the long axis of Tr along the out-of-plane (X) direction. It is easy to see that the calculated deformation of Tr structure resembled the one which was obtained following the “7b2g” vibration – see Fig. 7. Therefore it was not surprising that in the calculated spectrum, presented in Fig. 10, next to the dominating “ag” vibronic line we got the “177 cm−1” line, relative of the “b2g” vibration in planar Tr. In the calculated spectrum there were observed also some other lines, but with much lower intensity, indicating that the symmetry of the deformed Tr is similar to C2h, but not perfectly.
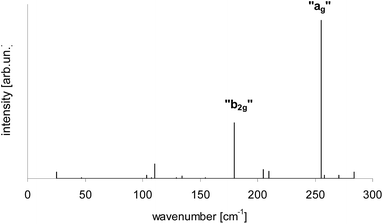 | ||
| Fig. 10 Calculated vibronic intensities in the spectrum of Tr molecule in a 2,3-DCN crystal estimated as the square of the scalar products of the vectors describing geometrical differences in the electronic ground S0 and lowest excited S1 states (see Table S9†). | ||
Experimental
Synthesis of 2,3-DCN and 2,3-DBN
Details of the synthesis are given in the ESI.†X-ray crystallography
The diffraction data for 2,3-DCN and 2,3-DBN crystals were collected on a SuperNova diffractometer at 120 K using the CuKα radiation (λ = 1.54184 Å). The data were corrected for Lorentz and polarization effects. A multi-scan absorption correction was applied. The structures were solved by direct methods using the SHELXS-97 program and refined by the full-matrix least-squares method on F2 using the SHELXL-97 program.31 The non-hydrogen atoms were refined with anisotropic displacement parameters. The C-bonded H-atoms were positioned geometrically and allowed to ride on the attached atom.Optical studies
Single crystals of zone-refined 2,3-DCN and 2,3-DBN lightly doped with Tr (dopant concentration of the order of 10−12 moles per mole) were obtained by co-sublimation of both components in argon gas atmosphere (∼0.2 atm) at a tube temperature close to 150 °C. Tr was purchased from the Institute für PAH-Forschung (Greifenberg, Germany) and used as received. Single crystals in the form of thin plates, especially those of 2,3-DBN, appeared to be very fragile and had to be treated with a big care in order to avoid breaking. Crystals were attached to a sample holder and inserted into a cryostat, which temperature could be stabilized at any value between 5 and 300 K. Cryostat was part of a home-made confocal microscope. The excitation source was a Coherent 700 dye laser (operating with Rh6G dye) pumped by a Verdi 5 laser: whole frequency 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 150–17
150–17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 cm−1, spectral resolution ∼1 cm−1. Laser light, applied along the crystal axis c, was focused to a near-diffraction limited spot of ∼0.45 μm diameter using a low temperature microscope objective (Bernhard Halle Nachfl. GmbH, Berlin, Germany). Fluorescence photons, transmitted through appropriate dielectric filters, were detected with a SPCM-AQR 14 photon counting module. More details about our confocal microscope can be found elsewhere.10
600 cm−1, spectral resolution ∼1 cm−1. Laser light, applied along the crystal axis c, was focused to a near-diffraction limited spot of ∼0.45 μm diameter using a low temperature microscope objective (Bernhard Halle Nachfl. GmbH, Berlin, Germany). Fluorescence photons, transmitted through appropriate dielectric filters, were detected with a SPCM-AQR 14 photon counting module. More details about our confocal microscope can be found elsewhere.10
Quantum-chemistry calculations
All calculations were done with the aid of the methods included in the Gaussian 09 package.32 The molecular geometry of Tr was conducted with B3LYP and TD B3LYP/6-31G(d,p) methods, while the vibronic spectra with method described in ref. 33. Tr in the crystals was treated by ONIOM methods, where Tr (ONIOM high level) was described by B3LYP/6-31G(d,p) and B3LYP/STO-3G methods, whereas the surrounding crystal (ONIOM low level) was described by UFF and PM3 methods. Geometry of Tr molecule was optimized in the electronic ground S0 and in the lowest excited S1 states. Vibrational frequencies for Tr in the crystal in the excited state were calculated only with TD B3LYP/STO-3G method, due to a too extended calculation time and a computer memory consumption. Crystallographic parameters (coordinates of the atoms in the molecule, and arrangement of molecules in the crystal unit) were taken as obtained by the X-ray diffraction studies performed in the present work.Conclusions
2,3-DCN and 2,3-DBN were synthesized and used to grow single crystals in the form of thin plates. The X-ray diffraction analysis showed that the crystal structures of both compounds are ordered where the weak and directional forces generate the herringbone packing of the constituting molecules.The crystals lightly doped with Tr provided the very good crystalline matrices for single molecule studies in the broad temperature range, from liquid helium to room temperature. The presence of heavy-atoms (Cl and Br) in the host crystals had only a little influence on the photo-physical parameters of the single Tr molecules. Triplet state population and depopulation rate constants were obtained from the analysis of fluorescence intensity correlation function and saturation of the vibronic lines observed in the fluorescence excitation spectrum. Negligible influence of the external heavy-atom effect on the intersystem crossing channel depopulating the fluorescence emitting singlet S1 state can be explained with the aid of the energy diagram of the electronic states of Tr, where the singlet S1 state is located far above the triplet T1 state and below the T2 state. Thus, single molecules of Tr in the investigated crystals are nearly as good emitters of fluorescence photons as in the systems without heavy-atoms.
Fluorescence excitation spectrum of single Tr molecules, within the scanning range of our laser, composed of the dominating purely electronic (0, 0) line, intense ag vibronic line of ∼250 cm−1 frequency and a new “184 cm−1” line. This last vibronic component is absent in the spectrum of isolated (D2h) Tr and was not observed in all previously investigated systems.
Appearance of the additional line in the fluorescence excitation spectrum visualizes deformation of the Tr molecule structure due to the interactions with the surrounding crystal molecules. Quantum-chemistry calculations performed for the different possible insertion sites, where Tr replaced three host molecules, allowed us to find the lowest energy configuration, where the short axis of Tr molecule, Y, is approximately parallel to the axis c of the crystal. Tr molecule in this site has the structure deformed like that induced by the “7b2g” vibration in planar Tr. In this mode symmetry of the molecule is lowered from D2h (characterizing planar Tr) to C2h. Calculated frequency of the “7b2g” line, 177 cm−1, is not far from the experimentally determined 184 cm−1.
The theoretical approach presented in this work may be applied to other systems where the surrounding matrix lowers symmetry of the guest molecules.
Acknowledgements
The work was financially supported by the National Science Centre, Poland, grant no. 2015/17/B/ST2/01744. Theoretical calculations were performed at the Interdisciplinary Centre of Mathematical and Computer Modelling (ICM) of the Warsaw University under computational grant no. G-32-10. X-ray crystallographic studies were carried out with the aid of equipment purchased thanks to the financial support of the European Regional Development Fund in the framework of the Operational Program Development of Eastern Poland 2007–2013 (Contract No. POPW.01.03.00-06-009/11-00, Equipping the laboratories of the Faculties of Biology and Biotechnology, Mathematics, Physics and Informatics, and Chemistry for studies of biologically active substances and environmental samples).Notes and references
- W. E. Moerner and L. Kador, Phys. Rev. Lett., 1989, 62, 2535 CrossRef CAS PubMed.
- M. Orrit and J. Bernard, Phys. Rev. Lett., 1990, 65, 2716 CrossRef CAS PubMed.
- W. E. Moerner, Angew. Chem., Int. Ed., 2015, 54, 8067 CrossRef CAS PubMed.
- M. Orrit, Angew. Chem., Int. Ed., 2015, 54, 8004 CrossRef CAS PubMed.
- B. Kozankiewicz and M. Orrit, Chem. Soc. Rev., 2014, 43, 1029 RSC.
- S. Kummer, F. Kulzer, R. Kettner, T. Basché, C. Tietz, C. Glowatz and C. Kryschi, J. Chem. Phys., 1997, 107, 7673 CrossRef CAS.
- L. Fleury, B. Sick, G. Zumofen, B. Hecht and U. P. Wild, Mol. Phys., 1998, 95, 1333 CrossRef CAS.
- M. Banasiewicz, D. Wiącek and B. Kozankiewicz, Chem. Phys. Lett., 2006, 425, 94 CrossRef CAS.
- N. Karl, H. Heymand and J. J. Stezowski, Mol. Cryst. Liq. Cryst., 1985, 131, 163 CrossRef CAS.
- R. Kościesza, E. Luzina, D. Wiącek, J. Dresner and B. Kozankiewicz, Mol. Phys., 2009, 107, 1889 CrossRef.
- M. Białkowska, W. Chaładaj, A. Makarewicz and B. Kozankiewicz, Acta Phys. Pol., A, 2015, 128, RK.3.1 CrossRef.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171 CrossRef CAS PubMed.
- 1,4-Dibromo and 1,4-dichloro: J. C. Bellows, E. D. Stevens and P. N. Prasad, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1978, 34, 3256 CrossRef CAS ; 1,5-Dibromo and 1,8-dibromo: R. C. Haltiwanger, P. T. Beurskens, J. M. J. Vankan and W. S. Veeman, J. Crystallogr. Spectrosc. Res., 1984, 14, 589 CrossRef ; 2,6-Dibromo: N. B. Chanh, A. Meresse, F. Leroy and S. Geoffre, Cryst. Struct. Commun., 1976, 5, 709 Search PubMed ; 2,6-Dichloro: T. L. Khotsyanova and Yu. T. Struchkov, J. Struct. Chem., 1964, 5, 375 CrossRef.
- The supplementary crystallographic data for 2,3-DBN and 2,3-DCN crystals are available respectively at CCDC 1509875 and 1509878.†.
- I. Novak, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2007, 63, o440 CAS.
- D. Wiącek and B. Kozankiewicz, Chem. Phys. Lett., 2008, 462, 280 CrossRef.
- T. Basché, W. E. Moerner, M. Orrit, and U. P. Wild, in Single-Molecule Optics, Detection, Imaging and Spectroscopy, VCH, Weinheim, 1996 Search PubMed.
- M. Białkowska, A. Makarewicz, M. Banasiewicz and B. Kozankiewicz, Chem. Phys. Lett., 2013, 555, 131 CrossRef.
- M. Banasiewicz, O. Morawski, D. Wiącek and B. Kozankiewicz, Chem. Phys. Lett., 2005, 414, 374 CrossRef CAS.
- I. Deperasińska, E. Karpiuk, M. Banasiewicz and B. Kozankiewicz, Chem. Phys. Lett., 2010, 492, 93 CrossRef.
- A. A. Gorshelev, A. V. Naumov, I. Y. Eremchev, Y. G. Vainer, L. Kador and J. Köhler, ChemPhysChem, 2010, 11, 182 CrossRef CAS PubMed.
- N. Navarro, Y. Tian, M. van Stee and M. Orrit, ChemPhysChem, 2014, 15, 3032 CrossRef PubMed.
- G. S. Harms, T. Irngartinger, D. Reiss, A. Renn and U. P. Wild, Chem. Phys. Lett., 1999, 313, 533 CrossRef CAS.
- R. Viruela-Martln, P. M. Viruela-Martln and E. Orti, J. Chem. Phys., 1992, 97, 8470 CrossRef.
- S. Karabunarliev, M. Baumgarten and K. Müllen, J. Phys. Chem. A, 1998, 102, 7029 CrossRef CAS.
- S. Karabunarliev, M. Baumgarten, E. R. Bittner and K. Müllen, J. Chem. Phys., 2000, 113, 11372 CrossRef CAS.
- I. Deperasińska, B. Kozankiewicz, I. Baktchantaev and J. Sepioł, J. Phys. Chem. A, 2001, 105, 810 CrossRef.
- T. M. Halasinski, J. L. Weisman, R. Ruiterkamp, T. J. Lee, F. Salama and M. Head-Gordon, J. Phys. Chem. A, 2003, 107, 3660 CrossRef CAS.
- P. Navarro, F. C. Bocquet, I. Deperasińska, G. Pirug, F. S. Tautz and M. Orrit, J. Phys. Chem. C, 2015, 119, 277 CAS.
- A. Berces and M. Zgierski, in Computational Molecular Spectroscopy, ed. P. Jensen and P. R. Bunker, Wiley, Chichester, 2000, p. 109 Search PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven Jr J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision B.01, Gaussian Inc., Wallingford CT, 2010 Search PubMed.
- (a) V. Barone, J. Bloino, M. Biczysko and F. Santoro, J. Chem. Theory Comput., 2009, 5, 540 CrossRef CAS PubMed; (b) J. Bloino, M. Biczysko, F. Santoro and V. Barone, J. Chem. Theory Comput., 2010, 6, 1256 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Details of synthesis, NMR spectra, additional optical results and details of quantum-chemistry calculations. CCDC 1509875 and 1509878. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c6ra27167g |
| This journal is © The Royal Society of Chemistry 2017 |