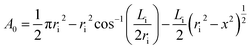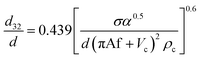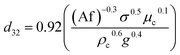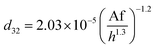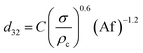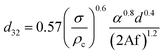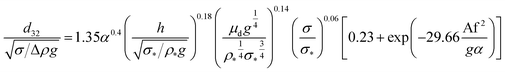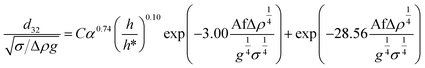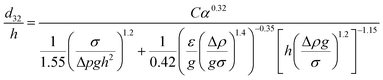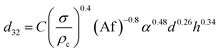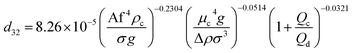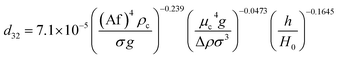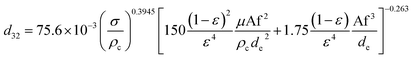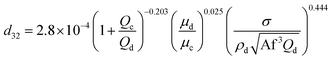Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Experimental investigation concerning the effect of mass transfer direction on mean drop size and holdup in a horizontal pulsed plate extraction column
Farhad Panahiniaa,
Mohammad Ghannadi-Maragheha,
Jaber Safdari *a,
Pouria Amanib and
Mohammad-Hassan Mallah
*a,
Pouria Amanib and
Mohammad-Hassan Mallah a
a
aNuclear Fuel Cycle Research School, Nuclear Science and Technology Research Institute, P. O. Box: 11365-8486, Tehran, Iran. E-mail: jsafdari@aeoi.org.ir; Tel: +98-21-88220473
bSchool of Chemical Engineering, College of Engineering, University of Tehran, P. O. Box: 11155-4563, Tehran, Iran
First published on 30th January 2017
Abstract
Vertical extraction columns meet the needs of industrial applications, but when height limitation (especially in indoor applications) is a concern it is required to use horizontal columns. Considering the significant role of mass transfer in the sizing and scale-up of horizontal extraction columns, no analytical and experimental investigations have been conducted in this regard. In the present research, the effect of operating parameters including pulsation intensity and phase flow rates on the mean drop size and the dispersed phase holdup values was investigated in a horizontal pulsed sieve-plate column under both mass transfer directions for the toluene–acetone–water, n-butyl acetate–acetone–water and butanol–acetone–water systems. The results show that holdup decreases first and then increases with an increase of pulsation intensity. Increasing dispersed phase velocity also increases holdup. The mean drop size decreases with an increment of pulsation intensity, whereas flow rates of both phases have little impact. Moreover, it is observed that the presence of mass transfer significantly affects the mean drop size and holdup. Finally, new correlations were proposed for the prediction of mean drop size and holdup based on operating variables and physical properties of the systems with and without mass transfer. Average Absolute Relative Error (AARE) of the correlations was between about 6.83–15.38% for their optimized constants.
1. Introduction
Solvent extraction is a classical method encountered in many industrial applications such as chemical, pharmaceutical environmental, oil, food, nuclear, and hydrometallurgical sectors for product purification and raw material recovery.1,2 This process is used typically when working with other separation methods such as distillation, evaporation and crystallization is not possible.3 To enhance the performance of extraction, many investigations have been implemented which have led to the introduction and development of a class of liquid–liquid contactors in which mechanical agitation is provided to increase the interfacial area between the two liquid phases. One type of these contactors is the pulsed sieve-plate extraction column, which requires external energy input in the form of pulsing motion usually sinusoidal superimposed on counter-current flow of the liquid phases. This pulsation provides high turbulence which assists in drop breakage. Consequently, the large interfacial area is obtained to get high mass transfer coefficient.4 Generally, pulsed columns compared to mixer-settlers, which commonly employ in the mining industry, are desirable from both safety and economic perspective, in particular their higher throughput, less space consumption, no internal moving parts, minimum leakage, and simplicity of design. The advantages are more beneficial especially while processing corrosive or radioactive solutions since the pulsing unit can be remote from the column. Pulsed sieve-plate columns can be divided into the vertical and horizontal contactors, and each has advantages and disadvantages that it is important to look for the specific process. Some investigations have focused on the main features of the horizontal and vertical types of extraction columns in identical conditions5–9 which show that the merits of vertical pulsed columns are more than horizontal ones. However, for some reasons horizontal pulsed columns are more desirable such as their higher performance in limited area.5,8,10One of the key parameters in the design and optimization of pulsed columns is the mean drop diameter.11 Because it is inclusive with the interfacial area between the two phases for the mass transfer and it eases of modeling and calculation of column throughput ensues. Moreover, drop size highly affects the residence time of the dispersed phase, the velocity of the rising drops, holdup, consequently the maximum throughput of the column and together with the holdup, it determines the interfacial area available for mass transfer.12–15
Similar to drop size, dispersed phase holdup is an important design parameter affecting the column dimension, and also the overall mass transfer coefficient. The dispersed-phase holdup (φ) can be defined as the volume fraction of the extraction column which is occupied by the dispersed phase:
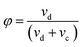 | (1) |
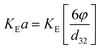 | (2) |
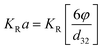 | (3) |
Numerous investigations have been carried out on the impact of the column geometry in pulsed extraction columns.18–20 It was achieved that the column diameter is almost ineffective on the mean drop size and the variation of drop sizes are more intense in initial internal plates. Due to the importance of mean drop size, many researches were implemented on the impact of operating variables including the pulsation intensity (Af) and flow rates of the dispersed and the continuous phases on drop size as well as introducing correlations for prediction of mean drop size in pulsed columns.10,12,13,21–31 Moreover, the evaluation of the dispersed phase holdup in different conditions is also studied by many investigators.5,16,26,29,32–38
In the absence of pulsation, interfacial tension and buoyancy are the cause of the drop breakage,13,20 while in the presence of pulsation, a smaller drop is formed as a consequence of an intensified collision between the drops and the internal plates and the internal wall, which causes a higher breakage rate.10,30,39,40 Also it is achieved that increasing the flow rate of both phases lead to a slight increase in mean drop diameter which was in accordance with other studies.18,25,29,30,41
According to literature, an increase in the fractional free area or plate spacing reduces the shear forces on drops resulting in an increase in drop size which leads to reduction in holdup. Holdup is a strong function of the dispersed phase velocity (Vd) and an increase in Vd increases holdup.4,42 However, the effect of continuous phase velocities (Vc) on holdup has been found be negligible.43,44 Yadav and Patwardhan20 presented a well review on the design aspects of pulsed sieve-plate columns, considering investigations on flow regimes in pulsed plate columns, flooding characterization, drop size, holdup and mass transfer as well as comparing proposed correlations for these variables. However, in spite of extensive work and various correlations which are available in the literature related to these hydrodynamic parameters in the vertical pulsed sieve-plate columns, the investigations on the horizontal pulsed sieve-plate columns are scarce. In particular, Khajenoori et al.,10 have studied the effect of operating parameters on the drop size as well as drop size distribution in a horizontal pulsed sieve-plate column and proposed a correlation for prediction of mean drop size and drop size distribution as a function of physical properties and operating parameters in the absence of mass transfer. Moreover, slip and characteristic velocities of both phases have been studied by the same author.45
Considering the significant role of mass transfer in the sizing of extraction columns, no analytical and experimental investigations have been conducted into the impact of mass transfer direction on the mean drop size and dispersed phase holdup for the horizontal sieve-plate columns. Therefore, presenting a reliable estimation of the mean drop size as well as holdup for this type of column in different operating conditions is needed. In this work, the Sauter-mean diameter and holdup value with the mass transfer in both directions have been investigated in a horizontal pulsed plate column. The effects of operating parameters including pulsation intensity and flow rates of the continuous and dispersed phases on drop size and the dispersed phase holdup have been studied. In addition, a theoretical–experimental correlation for Sauter drop size as well as holdup in terms of the operating conditions and the physical properties of chemical systems is proposed.
2. Experimental
2.1. Description of equipment
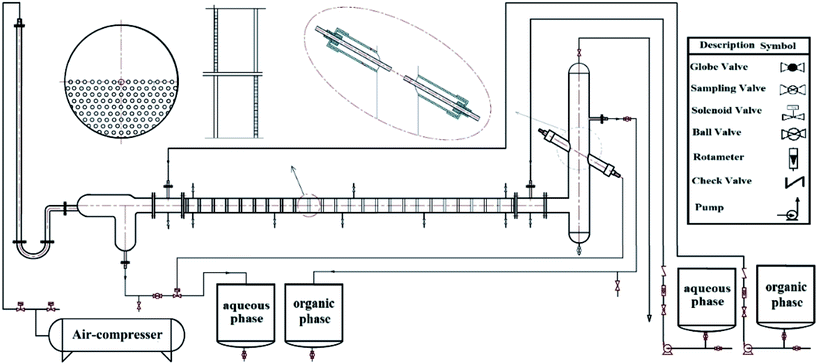
Experiments were carried out in a semi-industrial pulsed sieve-plate column. A glass pulsed column in horizontal position with an internal diameter of 6.2 cm and length of the active area of 146 cm was used in these experiments. The active part of column was a pipe housing an internal plate cartridge consisting of 25 pairs of sieve plates constructed from stainless steel 304. The plates are half-perforated and the holes laid on triangular pitch of 4 mm. The pulsation applied to the liquid by the pressure of air compressor and controlled by two solenoid valves. Due to counter-current flow of two liquid phases, each of them in the opposite direction of another side columns are imported so that the light phase interred in direction of applying pulsation. To control the liquid level in the column and regulate the discharge of heavy phase, an optical sensor in the collecting tank, in the output of the light phase, is embedded. Two settlers at both ends of the column were employed to separate the two liquid phases. The inlet and outlet streams of the column were connected to four tanks, each of 25 liters capacity. The flow rates of the two phases were measured by two rotameters. For more information, the column characteristics are listed in Table 1. Also, a schematic diagram of experimental apparatus is shown in Fig. 1.| Characteristics | Values |
|---|---|
| a Spacing between two individual plates in a cell.b Spacing between two adjacent cells. | |
| Column length (m) | 1.46 |
| Column diameter (cm) | 6.2 |
| Material of construction the column | Glass |
| Upper and lower settler diameter (cm) | 9 |
| Lower settler length (cm) | 30 |
| Upper settler length (cm) | 60 |
| Material used for plates, spacers and rod | Stainless steel |
| Holes pitch (mm) | 4 |
| Holes diameter (mm) | 2 |
| Plates thickness (mm) | 1 |
| Plate spacing (cm) | 1a, 5b |
| Average free area of the plates (%) | 0.11 |
2.2. Chemical system
Three liquid–liquid systems were chosen to cover a wide range of values of interfacial tension (1.5–30 mN m−1). The chemical system used for testing were toluene, n-butyl acetate and butanol as the light phase (dispersed phase) and distillated water as the heavy phase (continuous phase) with 3% volume fraction of acetone dissolved in each of the phases regarding the considered direction of mass transfer. Technical grade solvents of at least 99.5 wt% purity were used as the dispersed phase and all experiments were carried out at the temperature 20 °C. The physical properties of these systems are listed in Table 2. The viscosities of both phases are measured by a laboratory LAUDA viscometer. The densities are determined by use of a scale in order of 0.0001 g. It should be noted that, under mass transfer conditions, a degree of uncertainty surrounds the estimation of physical properties (particularly interfacial tension), since these vary not only with the inlet solute concentrations, but also along the column. In the present research, the values of physical properties have been assumed to correspond to the mean values of acetone concentration in the continuous and dispersed phases. The mean value of acetone concentration was obtained by averaging the values obtained at the inlet and outlet of the column.| Physical property | 3% volume fraction of acetone as mass transfer agent | ||
|---|---|---|---|
| Toluene–acetone–water | Butyl acetate–acetone–water | n-Butanol–acetone–water | |
| ρc (kg m−3) | 988.3–996.8 | 989.3–997.6 | 987.6–997.1 |
| ρd (kg m−3) | 861.2–865.2 | 876.9–882.3 | 837.9–848.3 |
| μc (mPa s) | 1.03–1.2 | 1.07–1.16 | 1.12–1.31 |
| μd (mPa s) | 0.56–0.58 | 0.7–0.74 | 3.26–3.34 |
| σ (mN m−1) | 20.5–33.2 | 10.9–13.2 | 1.5–1.9 |
2.3. Analytic procedure
Initially, both phases were mutually saturated each other before adding acetone in order to avoid the excessive dissolution of the dispersed phase into the continuous phase. This is a very essential step in the experiments since the volume fraction of acetone is 3% and the excessive dissolution of each phase to the other liquid might significantly affect the hydrodynamic and mass transfer performance of the column. After complete separation, they were transferred to the feed tanks. At the beginning of each run, the column was filled completely with distillated water. Dispersed phase was then entered to the column. After adjusting the flow rate of each phase based on the operating conditions, the pulsation intensity with specified amplitude and frequency was applied to the setup. All experiments were carried out under flooding conditions and sufficient time, 60–120 min depending on the phase flow rates and the particular liquid–liquid system used was provided for reaching the steady state conditions.Drop size was measured by taking digital images of the contents of the column using a Nikon D3100 camera. Drop sizes were measured on the 5 stages of the column which were equidistant from each other. To calculate the size of drops, images were analyzed by AutoCAD software. Indeed, the diameter of the column and the distance between two plates were set on their known values to provide a coordinate grid for measuring the drop sizes. 300 drops were analyzed in each experimental condition. A picture of drops, for instance, is shown in Fig. 2.
The most commonly-used representative diameter which used to study the mean drop size in the solvent extraction columns is Sauter mean diameter. The Sauter mean diameter (d32) was calculated at the experimental conditions by using the following relation:
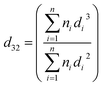 | (4) |
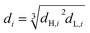 | (5) |
During measurements of drop sizes, each measurement was repeated three times and the average value was considered to guarantee the statistical significance of the determined variables.
Furthermore, the dispersed phase holdup was measured using a shutdown method. Based on this technique, the column was allowed to operate at the desired conditions until steady state was reached, after which the flow rates and pulsation were simultaneously stopped. Since the flow resistance through the plates was larger than the driving buoyancy forces, the liquid presented in each cell was effectively trapped. Therefore, after complete settlement of phases, the volume fraction occupied by each phase was determined by measuring the arc length of the part of the circumference wetted by the phases. The cord length at the interface (Li) was calculated from this measurement:
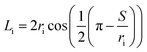 | (6) |
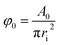 | (7) |
The Average Absolute Relative Error (AARE) was used as an objective function to calculate the fitted parameters:
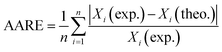 | (8) |
3. Results and discussion
3.1. Study of Sauter mean diameter
It is clear that drop diameter depends upon the rate of drop breakage and coalescence. Due to the turbulence produced by the pulsation, the drops will be driven through the plate perforations along with hitting of drops with the wall and plate holes which leads to smaller drops. On the other hand, the coalescence will induce rectification of liquid drops into larger ones. The main operating parameters found to influence mean drop are the phase flow rates and pulsation intensity. The effect of pulsation intensity on Sauter-mean drop diameter at both mass transfer directions is shown in Fig. 3. It is clear that drops produced from the high interfacial tension system (toluene–acetone–water) is larger than those produced from the medium and lower interfacial tension systems. It can also be observed that the effect of pulsation intensity on the mean drop size of high interfacial tension system is larger than that of other systems. Drops become smaller with the increase of pulsation intensity due to intense collision of the organic phase with trays and column wall and breaking into the smaller drops. Regarding to the mass transfer direction, it is clear that larger drops will be produced in the direction from the dispersed phase to the continuous phase, which are achieved in all systems. Also, the effects of pulsation intensity on the mean drop size are similar in both directions which means that the impact of pulsation intensity is effectless of the direction of mass transfer.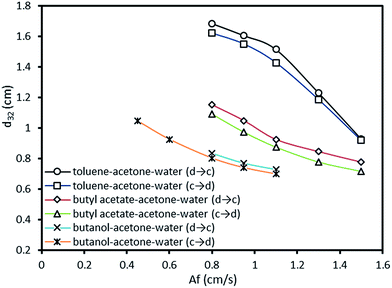 | ||
| Fig. 3 Effect of pulsation intensity on the mean drop size at constant dispersed and continuous phase flow rates of 2.1 and 5 l h−1. | ||
Furthermore, in another investigation by Khajenoori et al.,10 the effect of operating parameters on the mean drop size was studied which their results are compared with the experimental data from this work due to the same column used in both studies. For instance, the variation of mean drop size versus pulsation intensity obtained from this work and Khajenoori et al.,10 for constant dispersed and continuous phase flow rates of 2.1 and 5 l h−1 is illustrated in Fig. 4. The results show that the presence of mass transfer highly affects the mean drop size in following manner:
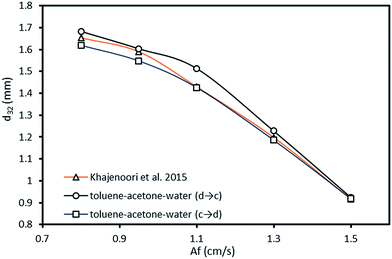 | ||
| Fig. 4 Variation of mean drop size versus pulsation intensity under different mass transfer conditions obtained from this work and Khajenoori et al.,10 at constant dispersed and continuous phase flow rates of 2.1 and 5 l h−1. | ||
• The presence of solute (3% volume fraction of acetone dissolved in each of the phases is considered in this study) is along with the evolution of the interfacial tension. According to Míšek et al.,46 the interfacial tension declines with increasing the solute concentration. Therefore, it is almost impossible to determine the drop breakage via the constant interfacial tension in the presence of mass transfer, whereas the gradient of interfacial tension is of most importance.
• When there is mass transfer from the continuous phase to the dispersed phase, smaller drops are produced in comparison to the same condition without mass transfer. In fact, because of the consequent interfacial tension gradient, the interface movement of the drop and the inner circulation generated into the drop gain the same direction. Therefore, this mass transfer direction leads to an increase in the interface deformations, consequent deformation of drops and higher drop breakage.
• When mass transfer occurs from the dispersed phase into the continuous phase, larger drops are observed in comparison to the same condition without mass transfer and with the reverse direction of the mass transfer. It is expected due to the opposite interfacial tension gradient compared to the reverse direction of the mass transfer. Therefore, in this case, the drops are consequently more stable than the former case. The effect of mass transfer direction on the mean drop size with increasing the pulsation intensity for the toluene–acetone–water system is shown in Fig. 4.
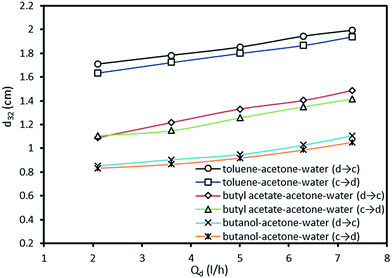
The effect of dispersed phase flow rate on the mean drop size in both directions of mass transfer is shown in Fig. 5. Increasing the flow rate of the dispersed phase leads to an increase in the drop size. With respect to Fig. 3, the impact of dispersed phase flow rate is found to be weaker than the influence of pulsation intensity on the mean drop size. The increase of drop size may be attributed to an increase in the coalescence rate due to the larger values of the dispersed phase holdup that are observed as the dispersed phase flow rate increases. From Fig. 5 also can be found that the drop size with mass transfer direction from the dispersed phase to the continuous phase is larger than that with the one determined in the inverse mass transfer direction.
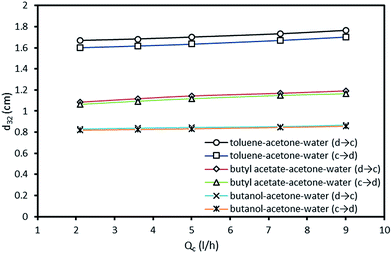
The effect of continuous phase flow rate on Sauter-mean drop size with both mass transfer directions is illustrated in Fig. 6. It is observed that the mean drop diameter slightly increases with an increase in the continuous phase flow rate. It is because of the fact that higher flow rate provides longer residence time due to the reduction of slip velocity between the drops and the continuous phase, which leads to higher probability for drop coalescence, and consequently producing larger drops.
3.2. Study of holdup
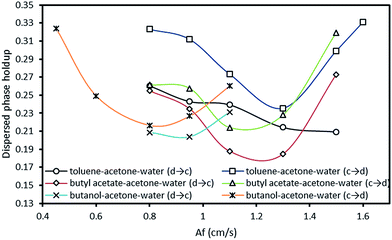
Dispersed phase holdup is necessary for calculating the interfacial area and the slip velocity of phases. It also indicates the onset of flooding. Dispersed phase holdup is a function of operating parameters such as pulsation intensity and flow rates of both phases which is investigated in the following.The influence of pulsation intensity on the dispersed phase holdup with both mass transfer directions is illustrated in Fig. 7. It is found that holdup in the high interfacial tension system (toluene–acetone–water) is larger than that in the other systems. This phenomenon is in an opposite manner to the results obtained in a the vertical pulsed plate column in previous investigations.29 As can be seen from the graph, the dispersed phase holdup exhibited two different behaviors with increasing the pulsation intensity, which can be referred to the operating regimes of the column. More information on the governing regimes in the horizontal pulsed sieve-plate column can be observed in Melnyk et al.,5 Khajenoori et al.,45 and Akhgar et al.,17 in which three regimes including fully separated, pseudo dispersion and emulsion regimes were characterized. Accordingly, at lower pulsation intensities which the column operates in the mixer-settler regime (fully separated flow regime), drops accumulate above of the column and the holdup values are high. With further increase of the pulsation intensity, holdup declines reaching to a minimum value within the dispersed regime. Therefore, holdup decreases with an increase in pulsation intensity in this regime. As the upper flooding limit is approached, holdup strongly increases and smallest drop fractions are washed out by the continuous phase. It can be also observed that the dispersed phase holdup with mass transfer direction from the continuous phase to the dispersed phase has larger values than that with the opposite direction. In fact, holdup values are higher with the mass transfer direction from the continuous phase to the dispersed phase than those measured with no mass transfer, and even higher than those measured when acetone transferred in reverse direction. As discussed in Section 3.1, this is due to the evolution of interfacial tension with the direction of mass transfer. This phenomenon is called Marangoni effect.47 Generally, higher holdup values can be found with mass transfer direction from the continuous phase to the dispersed phase, leading to higher performances but earlier flooding points.
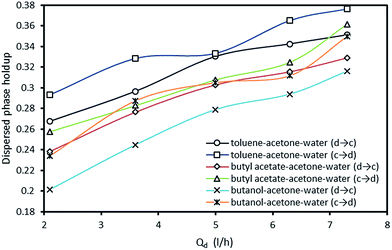
The effect of the dispersed phase flow rate on holdup with both two directions of mass transfer is shown in Fig. 8. It is observed that increasing the flow rate of the dispersed phase leads to an increase in the dispersed phase holdup. With respect to Fig. 7 and 8, the impact of pulsation intensity on holdup is found to be stronger than the effect of the dispersed phase flow rate as similar trends are observed for the mean drop diameter. Regarding to the presence of mass transfer, the flow rate of the dispersed phase shows similar impact on the holdup values in both directions of mass transfer.
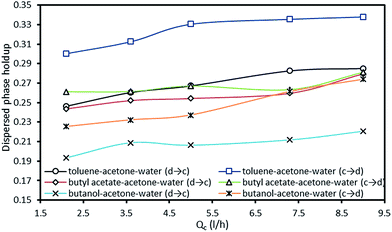
The variation of the dispersed phase holdup versus the continuous phase flow rate is illustrated in Fig. 9. It is revealed that the holdup slightly increases with an increase in the continuous phase flow rate, due to the higher drag forces. Also, it should be noted that the influence of the dispersed phase flow rate is found to be stronger than that of the continuous phase.
By considering Fig. 3–9, it is clear that in spite of the fact that the presence of mass transfer along with its direction highly influence the mean drop size and the dispersed phase holdup, operating parameters show similar impact on the hydrodynamic behavior of the column with and without mass transfer. However, the range of operating regimes are changed and consequently holdup shows oscillatory behavior with increasing the pulsation intensity.
3.3. Predictive correlation for mean drop size
Numerous correlations have been proposed for prediction of mean drop size in various pulsed extraction columns such as packed, sieve-plate and disc and doughnut columns.20 However, most of these correlations are related to vertical pulsed columns and cannot be used in other types of extraction columns including horizontal ones since the impact of operating parameters on the hydrodynamic behaviour of a horizontal extraction column is distinctive from that in the vertical columns. Table 3 exhibits a number of available correlations proposed to predict the mean drop size in pulsed columns.Furthermore, Yadav and Patwardhan20 have presented a review on the proposed correlations on the mean drop size in vertical pulsed sieve-plate columns. They compared experimental data of 6 different investigations with the available correlations and it was concluded that the correlation of Sreenivasulu et al.,52 is much better than other correlations and it is recommended to be used for prediction of mean drop size in vertical pulsed sieve-plate columns. Sreenivasulu et al.,52 proposed the following correlation:
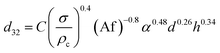 | (9) |
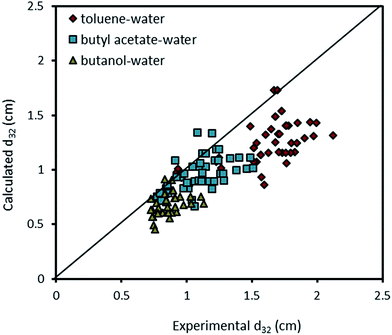
Fig. 10 compares the experimental data obtained with the presence of mass transfer (d → c) in the horizontal pulsed plate column with the prediction using eqn (9). Although eqn (9) is approximately able to estimate the mean drop size, it is inaccurate in some experiments and also it is not able to cover all effective parameters. Therefore, another correlation is needed.
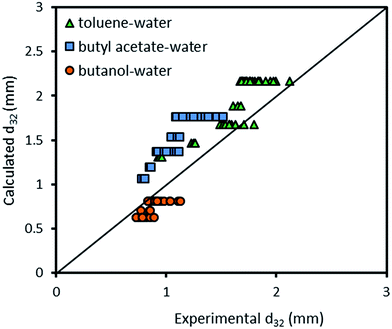 | ||
| Fig. 10 Comparison of experimentally-measured mean drop size with the calculated values by eqn (9) for different chemical systems. | ||
In another study, Khajenoori et al.,10 have developed a semi empirical correlation for prediction of the mean drop size in a horizontal pulsed column for three different systems without mass transfer, which covers the effect of operating parameters and physical properties of the liquid systems. They proposed following correlation:
 | (10) |
The experimental data with the presence of mass transfer are compared with the correlation proposed by Khajenoori et al.,10 and the results are illustrated in Fig. 11. It is found that eqn (10) is not able to satisfactorily predict the mean drop size with the presence of mass transfer. Since there is no correlation for prediction of mean drop size in the horizontal pulsed plate column, there is a need to propose a correlation as a function of operating parameters and physical properties.
 | ||
| Fig. 11 Comparison of experimentally-measured mean drop size with the calculated values by eqn (10) for different chemical systems. | ||
Consequently, for prediction of mean drop size, a new theoretical–experimental correlation is developed in terms of physical properties of the systems and operating parameters by dimensional analysis methods (Buckingham's pi-theorem):
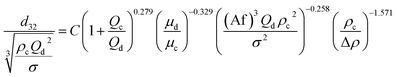 | (11) |
| Data source | Mass transfer | C | AARE (%) |
|---|---|---|---|
| Khajenoori10 | None | 1.342 | 16.24 |
| This study | c → d | 1.323 | 7.89 |
| This study | d → c | 1.381 | 7.83 |
The comparison of the experimental data with those calculated by eqn (11) is illustrated in Fig. 12. This figure shows the accuracy of the derived equation to predict the mean drop size with and without mass transfer.
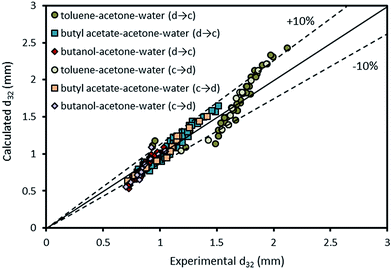 | ||
| Fig. 12 Comparison of experimentally-measured mean drop size with the calculated values by eqn (11) for different chemical systems in the presence of mass transfer in both directions. | ||
3.4. Predictive correlation for holdup
As shown in Fig. 7–9, the dispersed phase holdup is a function of operating parameters including the pulsation intensity and flow rates of both phases as well as physical properties of the systems as follows:| φ = f(Qc,Qd,Af,μd,μc,σ,ρc,ρd) | (12) |
Many holdup correlations have been proposed but most of them are related to the vertical pulsed column.20 Some of available correlations for prediction of holdup are listed in Table 5.
| Reference | Pulsed column type | Correlation |
|---|---|---|
| 48 | VPSPC | φ = 4.93 × 102ψ0.84Vd2/3 |
| φ = 3.42 × 106ψ0.24Vd2/3 | ||
| 53 | VPSPC | 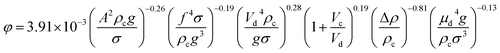 |
| 53 | VPSPC | 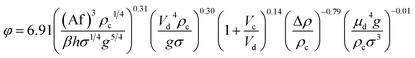 |
| 53 | VPSPC | 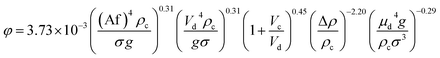 |
| 54 | VPSPC | 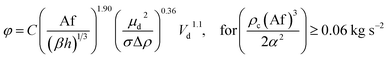 |
| 44 | VPSPC | 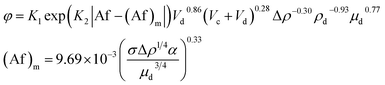 |
| 55 | VPSPT | φ = K1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(K2|Af − (Af)m|)Vd1.02Vc0.02Δρ−0.23μd0.52d−0.3α−0.4h−0.4 exp(K2|Af − (Af)m|)Vd1.02Vc0.02Δρ−0.23μd0.52d−0.3α−0.4h−0.4 |
| 5 | HPSPC | 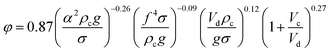 |
| 56 | VPPC | 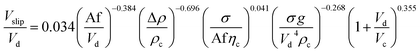 |
Holdup can be calculated from following equation: 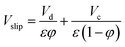 |
||
| 57 | PDDC | Mixer-settler 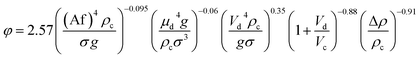 |
Transition and emulsion 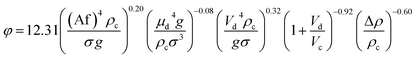 |
||
| 42 | VPPC | 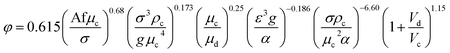 |
| 45 | HPSPC | 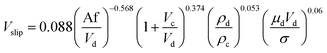 |
Holdup can be calculated from following equation: 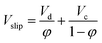 |
Melnyk et al.,5 presented following correlation for prediction of overall average holdup as a function of operating parameters by using several available experiments on the flooding results of the horizontal pulsed plate column:
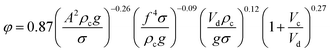 | (13) |
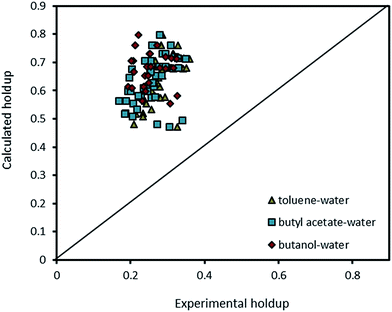 | ||
| Fig. 13 Comparison of experimental holdup with the calculated values by eqn (13) for different chemical systems. | ||
In another study, Khajenoori et al.,45 studied the effect of operating parameters on slip and characteristic velocities in a same horizontal pulsed sieve-plate column for the four chemical systems without mass transfer. They proposed the following semi-empirical correlation for prediction of the slip velocity:
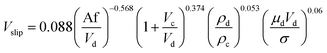 | (14) |
When two immiscible phases flow counter-currently through an extraction column without packing, the following relationship between the slip and superficial velocities and holdup values can be defined:58
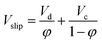 | (15) |
Therefore, combining eqn (14) with (15) results in a correlation which can estimate the holdup of the column. Fig. 14 compares experimental results with data calculated by the correlation proposed by Khajenoori et al.45 It is observed that it is not able to cover the experimental data very accurately. However, it should be noted that the correlation proposed by Melnyk et al.,5 and Khajenoori et al.,45 are presented for different chemical systems without mass transfer and they did not consider the remarkable influence of the presence of mass transfer on the dispersed phase holdup of the column.
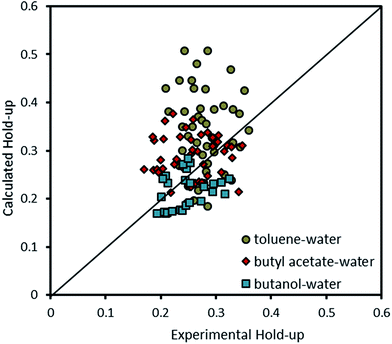 | ||
| Fig. 14 Comparison of experimental holdup with the calculated values by eqn (15) for different chemical systems. | ||
Therefore, according to eqn (12), a new theoretical–experimental correlation is proposed for prediction of the dispersed phase holdup in terms of physical properties of the liquid systems and operating parameters by dimensional analysis methods:
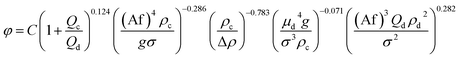 | (16) |
| Data source | Mass transfer | C | AARE (%) |
|---|---|---|---|
| Khajenoori45 | None | 0.97 | 15.47 |
| This study | c → d | 0.101 | 8.02 |
| This study | d → c | 0.089 | 6.36 |
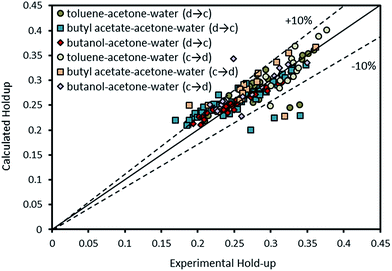 | ||
| Fig. 15 Comparison of experimental holdup with the calculated values by eqn (16) for different chemical systems. | ||
3.5. Comparison between the hydrodynamic of different extraction columns
One of the objectives of this research was to evaluate the benefits of the application of the horizontal extraction columns in industrial applications. Kagan et al.,22 Miyauchi and Oya,48 and Kleczek et al.,59 are among the researches who have conducted some experiments on mean drop size in standard vertical pulsed columns with almost similar operating conditions and column dimensions to the horizontal column used in this study. Tables 7 and 8 presents the operating and geometrical conditions for these investigations and physical properties of the systems used, respectively. By comparing the values of the mean drop size in different operating conditions reported in these studies with the experimental data of this work, one can observed that smaller droplets can form in a horizontal pulsed sieve-plate extraction column compared to the standard vertical pulsed plate columns in almost identical conditions. For better demonstration between the values of mean drop size in vertical and horizontal columns, Fig. 16 exhibits the mean drop size in the current study and those obtained from the correlations proposed by Kagan et al.22 Miyauchi and Oya48 and Kleczek et al.59 versus pulsation intensity. It can be observed that exerting pulsation into a horizontal plate extraction column forms smaller droplets compared to vertical plate extraction column.| Descriptions | Parameters | Investigators | ||
|---|---|---|---|---|
| Kagan et al.22 | Miyauchi and Oya48 | Kleczek et al.59 | ||
| Column dimension | D × 103 (m) | 56 | 54 | 67 |
| H (m) | 5.4 | 0.37–0.86 | 0.7 | |
| Plate details | d × 103 (m) | 2 | 3 | 3 |
| α | 8.2 | 0.19 | 0.067–0.134 | |
| h × 103 (m) | 50 | 30–70 | 50 | |
| Material | SS | SS | — | |
| Pulse details | f (Hz) | 0.8–1.67 | 3 | — |
| A × 103 (m) | 5–15 | 1.7–15 | — | |
| Af (m s−1) | 4–25 | 5.1–45.0 | 8–21 | |
| Phase velocities | Vc × 103 (m s−1) | 6.2–6.7 | 2.7 | 4.25 |
| Vd × 103 (m s−1) | 0.6–1.2 | 0.43 | 4.25 | |
| Experimental details | Investigators | ||
|---|---|---|---|
| Kagan et al.22 | Miyauchi and Oya48 | Kleczek et al.59 | |
| Continuous phase (c) | Water | Water | Water, glycerine |
| Dispersed phase (d) | Kerosene | MIBK | Benzene, toluene, xylene, butyl acetate, carbon tetrachloride and chloroform |
| Solute | — | — | Acetic, propionic, butyric and benzoic acids, acetone, phenol and iodine |
| Mass transfer direction | — | — | c → d, d → c |
| ρc (kg m−3) | 1000 | 996.38 | 1000–1054 |
| ρd (kg m−3) | 788.69 | 796.13 | 860–1600 |
| μc × 103 (Pa s) | 1 | 0.842 | 1–1.7 |
| μd × 103 (Pa s) | 1.7584 | 0.554 | 0.6–0.97 |
| σ × 103 (N m−1) | 39.0 | 10.3 | 11.1–41.2 |
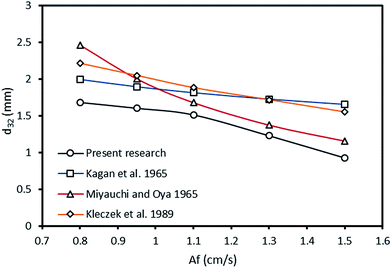 | ||
| Fig. 16 Mean drop size versus pulsation intensity at dispersed and continuous phase flow rates of 2.1 and 3.6 l h−1 for toluene–acetone–water. | ||
4. Conclusions
In industrial applications with space constraints, using horizontal columns is much beneficial compared to the standard vertical columns due to higher interfacial area available for mass transfer and consequently lower required area. Considering the significant role of mass transfer in the sizing and scale-up of horizontal extraction columns, no analytical and experimental investigations have been conducted in this regard. In this work, the effect of operating parameters including pulsation intensity as well as flow rates of the continuous and dispersed phases on mean drop size and holdup are investigated in a horizontal pulsed sieve-plate column under the presence of mass transfer in both directions. The results are illustrated and compared with the previous studies. The achievements of this work are summarized as follows:• An increase in the flow rate of the dispersed and the continuous phases results in an increase in the holdup along with producing larger drops. The direction of mass transfer do not alter affect the impact of operating parameters on mean drop size and holdup. However, it is observed that the variation in mean drop size and holdup with respect to the presence of mass transfer and its direction versus operating conditions is greater in higher values of mean drop size and holdup.
• With mass transfer from the continuous phase to the dispersed phase, smaller drops are produced in comparison with no mass transfer condition and even with mass transfer in the reverse direction due to the Marangoni effect.
• An increase in the pulsation intensity within the mixer settler regime leads to the reduction of holdup of the column, reaching to the minimum point which indicates the maximum throughput of the column. With further increase in pulsation intensity, it begins to increase.
• Holdup for the toluene–acetone–water system is found to be more than that for the butyl acetate–acetone–water and the butanol–acetone–water systems under the same operating conditions. This phenomenon is in an opposite manner to the results obtained in a standard vertical pulsed plate column in previous investigations.
• The comparison between the results of the current research and those in similar vertical extraction columns reveals that the horizontal pulsed extraction columns provide a larger mass transfer area and hence better mass transfer efficiency.
• Two new correlations in terms of the operating variables and physical properties of the liquid systems are developed for prediction of the mean drop size and holdup in a horizontal pulsed plate column in the absence and presence of mass transfer coefficient. The AARE values of the proposed correlations are between 6.36 and 16.24% for their optimized constants, which shows the good accuracy of presented correlations.
Nomenclature
| a | Specific interfacial area, m2 m−3 |
| A | Amplitude of pulsation, m |
| Af | Pulsation intensity, m s−1 |
| d32 | Sauter mean diameter, m |
| f | Frequency of pulsation, Hz |
| HPSPC | Horizontal pulsed sieve-plate column |
| PDDC | Pulsed disc and doughnut column |
| Q | Volumetric flow rate, m3 s−1 |
| V | Velocity, m s−1 |
| Vc | Superficial velocity of continuous phase, m s−1 |
| Vd | Superficial velocity of dispersed phase, m s−1 |
| Vslip | Slip velocity, m s−1 |
| VPPC | Vertical pulsed packed column |
| VPSPC | Vertical pulsed sieve-plate column |
| v | Kinematic viscosity, m2 s−1 |
Greek symbols
| α | Fractional free area |
| ε | Power dissipated per unit mass of fluid, W kg−1 |
| φ | Holdup |
| μ | Viscosity, N s m−2 |
| ρ | Density, kg m−3 |
![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) | Density of mixture of phases, kg m−3 |
| σ | Interfacial tension between two phases, N m−1 |
Subscripts
| c | Continuous phase |
| d | Dispersed phase |
| f | Flooding |
References
- A. Warade, R. Gaikwad, R. Sapkal and V. Sapkal, Leonardo J. Sci., 2011, 79–94 Search PubMed.
- P. Amani, J. Safdari, H. Abolghasemi, M. H. Mallah and A. Davari, Int. J. Heat Fluid Flow, 2017 DOI:10.1016/j.ijheatfluidflow.2017.01.003.
- L. S. Tung and R. H. Luecke, Ind. Eng. Chem. Process Des. Dev., 1986, 25, 664–673 CAS.
- N. Somkuwar, N. Kolhe and V. Rathod, Indian Chem. Eng., 2014, 56, 235–257 CrossRef CAS.
- A. J. Melnyk, S. Vijayan and D. R. Woods, Can. J. Chem. Eng., 1992, 70, 417–425 CrossRef CAS.
- A. A. A. Hussain, T.-B. T. Liang and M. M. J. Slater, Chem. Eng. Res. Des., 1988, 66, 541–554 CAS.
- J. Procházka and M. M. Hafez, Collect. Czech. Chem. Commun., 1972, 37, 3725–3734 CrossRef.
- D. Logsdail and J. Thornton, React. Technol., 1959, 1, 15–24 CAS.
- V. Vdovenko and S. Kulikov, Radiokhimiya, 1966, 8, 525–533 CAS.
- M. Khajenoori, A. Haghighi-Asl, J. Safdari and M. H. Mallah, Chem. Eng. Process., 2015, 92, 25–32 CrossRef CAS.
- S. Maaß, S. Wollny, A. Voigt and M. Kraume, Exp. Fluids, 2011, 50, 259–269 CrossRef.
- W. Pietzsch and T. H. Pilhofer, Chem. Eng. Sci., 1984, 39, 961–965 CrossRef CAS.
- A. Kumar and S. Hartland, Ind. Eng. Chem. Res., 1996, 35, 2682–2695 CrossRef CAS.
- N. A. Moraes, J. B. A. Paulo and G. S. Medeiros, Brazilian Journal of Petroleum and Gas, 2011, 5, 75–85 CrossRef.
- G. Zhou and S. M. Kresta, Chem. Eng. Sci., 1998, 53, 2063–2079 CrossRef CAS.
- W. Pietzsch and E. Blass, Chem. Eng. Technol., 1987, 10, 73–86 CrossRef.
- S. Akhgar, J. Safdari, J. Towfighi, P. Amani and M. H. Mallah, RSC Adv., 2017, 7, 2288–2300 RSC.
- N. M. Spaay, A. J. F. Simons and G. P. Ten Brink, in Proc. Internal. Solvent Extraction Conf., ISEC, 1971, vol. 71, pp. 19–23 Search PubMed.
- M. Lorenz, H. Haverland and A. Vogelpohl, Chem. Eng. Technol., 1990, 13, 411–422 CrossRef CAS.
- R. L. Yadav and A. W. Patwardhan, Chem. Eng. J., 2008, 138, 389–415 CrossRef CAS.
- T. Míšek, Collect. Czech. Chem. Commun., 1964, 29, 1755–1766 CrossRef.
- S. Kagan, M. Aerov, V. Lonik and T. Volkova, Int. Chem. Eng., 1965, 5, 656 Search PubMed.
- A. Assenov and I. Penchev, Dokl. Bolg. Akad. Nauk, 1971, 24, 1381–1387 Search PubMed.
- J. Kubica and D. Zdunkiewicz, Inz. Chem., 1977, 7, 903–907 CAS.
- L. Boyadzhiev and M. Spassov, Chem. Eng. Sci., 1982, 37, 337–340 CrossRef CAS.
- H. Schmidt, Chem. Eng., McGraw-Hill, Pub., Co, 1983, pp. 164–165 Search PubMed.
- H. Vassallo, G. Thornton and J. D. Dworschak, Proc. Int. Solvent Extr. Conf., 1983, 1, 168–169 Search PubMed.
- R. Yaparpalvi, P. K. Das, A. K. Mukherjee and R. Kumar, Chem. Eng. Sci., 1986, 41, 2547–2553 CrossRef CAS.
- A. Prabhakar, G. Sriniketan and Y. B. G. Varma, Can. J. Chem. Eng., 1988, 66, 232–240 CrossRef CAS.
- M. Gholam Samani, A. Haghighi Asl, J. Safdari and M. Torab-Mostaedi, Chem. Eng. Res. Des., 2012, 90, 2148–2154 CrossRef CAS.
- Y. Wang, K. H. Smith, K. A. Mumford, H. Yi, L. Wang and G. W. Stevens, Chem. Eng. Res. Des., 2016, 109, 667–674 CrossRef CAS.
- D. Venkatanarasaiah and Y. B. G. Varma, Bioprocess Eng., 1998, 18, 119–126 CrossRef CAS.
- G. U. Din, I. R. Chughtai, M. H. Inayat and I. H. Khan, Appl. Radiat. Isot., 2008, 66, 1818–1824 CrossRef CAS PubMed.
- G. A. Sehmel and A. L. Babb, Ind. Eng. Chem. Process Des. Dev., 1963, 2, 38–42 CAS.
- W. Batey, T. Arthur, P. Thompson and J. Thornton, Proc. Int. Solvent Extr. Conf., 1983, 1, 166–167 Search PubMed.
- V. G. Lade, V. K. Rathod, S. Bhattacharyya, S. Manohar and P. K. Wattal, Chem. Eng. Res. Des., 2013, 91, 1133–1144 CrossRef CAS.
- M. H. I. Baird and S. J. Lane, Chem. Eng. Sci., 1977, 28, 947–957 CrossRef.
- R. L. Bell and A. L. Babb, Ind. Eng. Chem. Process Des. Dev., 1969, 8, 392–400 CAS.
- M. R. Usman, H. Sattar, S. N. Hussain, H. Muhammad, A. Asghar and W. Afzal, Braz. J. Chem. Eng., 2009, 26, 677–683 CrossRef CAS.
- S. Ousmane, M. Isabelle, M. S. Mario, T. Mamadou and A. Jacques, Chem. Eng. Res. Des., 2011, 89, 60–68 CrossRef CAS.
- M. G. Samani, J. Safdari, A. H. Asl and M. Torab-Mostaedi, Chem. Eng. Technol., 2014, 37, 1155–1162 CrossRef CAS.
- M. Asadollahzadeh, J. Safdari, A. Haghighi-Asl and M. Torab-Mostaedi, Chem. Ind. Chem. Eng. Q., 2012, 18, 255–262 CrossRef CAS.
- Y. Wang, K. A. Mumford, K. H. Smith, Z. Li and G. W. Stevens, Ind. Eng. Chem. Res., 2016, 55, 714–721 CrossRef CAS.
- A. Kumar and S. Hartland, Chem. Eng. Process., 1988, 23, 41–59 CrossRef CAS.
- M. Khajenoori, J. Safdari, A. H. Asl and M. H. Mallah, Chem. Eng. Technol., 2015, 38, 1783–1792 CrossRef CAS.
- T. Míšek, R. Berger and J. Schröter, EFCE Publ. Ser., 1985, 46, 1 Search PubMed.
- C. Gourdon and G. Casamatta, Chem. Eng. Sci., 1991, 46, 2799–2808 CrossRef CAS.
- T. Miyauchi and H. Oya, AIChE J., 1965, 11, 395–402 CrossRef CAS.
- H. Angelino, C. Alran, L. Boyadzhi and S. P. Mukherje, Br. Chem. Eng., 1967, 12, 1893 CAS.
- A. Kumar and S. Hartland, Chem. Eng. Commun., 1986, 44, 163–182 CrossRef CAS.
- A. Kumar and S. Hartland, Liq.-Liq. Extr. Equip., 1994, 625–735 CAS.
- K. Sreenivasulu, D. Venkatanarasaiah and Y. B. G. Varma, Bioprocess Eng., 1997, 17, 189–195 CrossRef CAS.
- A. Kumar and S. Hartland, Chem. Eng. Res. Des., 1983, 61, 248–252 CAS.
- L. Tung and R. Luecke, Ind. Eng. Chem., 1986, 664–673 CAS.
- S. Dimitrova Al Khani, C. Gourdon and G. Casamatta, Ind. Eng. Chem. Res., 1988, 27, 329–333 CrossRef.
- F. T. Hokmabadi, H. Bahmanyar, M. Amanabadi and J. Safdari, Can. J. Chem. Eng., 2009, 87, 855–861 CrossRef CAS.
- M. Torab-Mostaedi, H. Jalilvand and M. Outokesh, Braz. J. Chem. Eng., 2011, 28, 313–323 CrossRef.
- J. D. Thornton, Chem. Eng. Sci., 1956, 5, 201–208 CrossRef CAS.
- F. Kleczek, V. Cauwenberg and P. Van Rompay, Chem. Eng. Technol., 1989, 12, 395–399 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2017 |