Open Access Article
Open Access ArticleNanofluidic osmotic power generators – advanced nanoporous membranes and nanochannels for blue energy harvesting
Gregorio
Laucirica
 a,
María Eugenia
Toimil-Molares
b,
Christina
Trautmann
bc,
Waldemar
Marmisollé
*a and
Omar
Azzaroni
a,
María Eugenia
Toimil-Molares
b,
Christina
Trautmann
bc,
Waldemar
Marmisollé
*a and
Omar
Azzaroni
 *a
*a
aInstituto de Investigaciones Fisicoquímicas Teóricas y Aplicadas (INIFTA), Departamento de Química, Facultad de Ciencias Exactas, Universidad Nacional de La Plata, CONICET, CC 16 Suc. 4, 1900 La Plata, Argentina. E-mail: wmarmi@inifta.unlp.edu.ar; azzaroni@inifta.unlp.edu.ar; Web: http://softmatter.quimica.unlp.edu.ar Web: http://www.twitter.com/softmatterlab
bGSI Helmholtzzentrum für Schwerionenforschung, 64291 Darmstadt, Germany
cTechnische Universität Darmstadt, Materialwissenschaft, 64287 Darmstadt, Germany
First published on 24th September 2021
Abstract
The increase of energy demand added to the concern for environmental pollution linked to energy generation based on the combustion of fossil fuels has motivated the study and development of new sustainable ways for energy harvesting. Among the different alternatives, the opportunity to generate energy by exploiting the osmotic pressure difference between water sources of different salinities has attracted considerable attention. It is well-known that this objective can be accomplished by employing ion-selective dense membranes. However, so far, the current state of this technology has shown limited performance which hinders its real application. In this context, advanced nanostructured membranes (nanoporous membranes) with high ion flux and selectivity enabling the enhancement of the output power are perceived as a promising strategy to overcome the existing barriers in this technology. While the utilization of nanoporous membranes for osmotic power generation is a relatively new field and therefore, its application for large-scale production is still uncertain, there have been major developments at the laboratory scale in recent years that demonstrate its huge potential. In this review, we introduce a comprehensive analysis of the main fundamental concepts behind osmotic energy generation and how the utilization of nanoporous membranes with tailored ion transport can be a key to the development of high-efficiency blue energy harvesting systems. Also, the document discusses experimental issues related to the different ways to fabricate this new generation of membranes and the different experimental set-ups for the energy-conversion measurements. We highlight the importance of optimizing the experimental variables through the detailed analysis of the influence on the energy capability of geometrical features related to the nanoporous membranes, surface charge density, concentration gradient, temperature, building block integration, and others. Finally, we summarize some representative studies in up-scaled membranes and discuss the main challenges and perspectives of this emerging field.
1 Introduction
The growing demand for energy on top of the concern due to environmental pollution has triggered active research to develop new efficient ways to obtain sustainable energy.1,2 Over the last few decades, methods based on wind, water, geothermal and solar sources have attracted special interest due to their reliability, availability, and technological potential.3–6 In this context, the possibility to obtain salinity gradient energy (SGE) (so-called salinity gradient power or blue energy) emerges as a promising candidate due to its great theoretical potential. SGE is based on the conversion of Gibbs free energy released from the mixing of solutions with different saline concentrations into electrical energy.7–9 It is estimated that energy of 0.8 kW h m−3 can be harnessed at the sea–river confluence exploiting the entropy changes involved in the mixing.10,11One of the pioneering studies related to this sustainable energy was published by R. E. Pattle in 1954.12 In this work, the author assures that the free energy involved when a river mixes with the sea is comparable to those obtainable for a waterfall of 680 ft (interestingly, nowadays the confluence is often referred to as the “silent waterfall”).8 Furthermore, the first reverse electrodialysis (RED) system was implemented by stacking cation and anion exchange membranes separated by alternating seawater and river water. Then, in 1974 Norman et al. designed a new way to harvest SGE by using osmotic membranes in a process called pressure retarded osmosis (PRO).13 Except for some pioneering studies and patents published around the nineteen seventies, the difficulty to create suitable membranes was hindering further advances in the field.14–16 Later on, advances in technology and materials science, and the development of more efficient membranes paved the way for extensive progress in this field,17,18 to the extent that, currently, there is a broad knowledge about different approaches to efficiently harness SGE either by membrane-based processes (e.g. RED and PRO) or electrochemical-based methods such as capacitive mixing.19–22 Also, some pilot plants have shown promising results demonstrating the real technological potential of the membrane-based SGE methods.23–27 However, conventional membranes containing subnanopores exhibit limited flux ion efficiency and it is difficult to further improve their properties.
In the last few decades, the development of new nanofabrication techniques with precise control at the nanometer scale has encouraged rapid and continuous growth in the study and design of nanodevices with a wide variety of applications.28,29 Motivated by the fascinating properties of biological ion channels and exploiting the concept of “learning from nature”, the creation of platforms based on solid-state nanochannels (SSNs) has attracted the attention of the scientific community.30–38 In this scenario, the development of membrane-containing SSNs appeared as promising components for energy harvesting systems.39–42 The immense potential of the combination of nanotechnology and energy-related applications rapidly captured the attention of the scientific community causing full and continuous progress in the field of nanoporous membrane-based energy harvesting.11,43
The possibility of this new generation of nanoporous membranes to operate as energy harvesters mostly comes from the presence of charged groups on the surface of nanometric pores (this property will be addressed in more detail below). So far, different methods to harvest energy using charged nanoporous membranes have been reported including streaming current,44 diffusion current,45 and diffusio-osmotic current.46 In some cases, the differences reside not only in the experimental set-up but also in the basic principles. The streaming current is generated by applying an external mechanical force such as a pressure drop.47,48 This fact establishes the selective transport of counter-ions in the electrical double layer which enables the conversion of an external mechanical force into electrical energy. Beyond its technological relevance, this method has also become useful for physicochemical surface characterization.49 On the other hand, the diffusion current is obtained by the exposure of an ion-selective nanoporous membrane to a gradient concentration.50,51 As detailed below, an asymmetric electrolyte concentration combined with the membrane permselectivity promotes a net flux of counter-ions across the membrane. This results in the creation of transmembrane potential and enables the conversion of Gibbs free energy of mixing into electrical energy without applying external forces. Finally, the diffusio-osmotic current is generated in a similar way to the diffusion current, but in contrast, the phenomenon involves the energy harvesting through the osmotic pressure gradient in the interfacial diffuse layer established by the salt concentration difference.46 The last two processes influence the SGE harnessing methods and are addressed in detail in this review.
The application of the new generation of nanoporous membranes is considered a promising strategy to exceed the commercial benchmark value of 5 W m−2 proposed in previous investigations for salinity gradient energy technologies.39,41,52–56 To achieve this goal, several strategies have been reported, most of them require both the development of membranes based on new materials and the integration of functional building blocks into the membrane pores to render unique features related to the ion selectivity and flux.57,58 However, considering the current state-of-the-art, the future of nanoporous membranes for RED remains controversial. In particular, while laboratory-scale experiments demonstrated the supremacy of the results obtained for nanoporous membranes over the traditional ones, much work is necessary to transfer these results into scaled-up systems. In particular, a close and interdisciplinary effort among engineering, materials science, nanotechnology, physical chemistry, and electrochemistry will play a crucial role in increasing energy conversion capabilities and make possible the scaling up of this technology (Fig. 1).
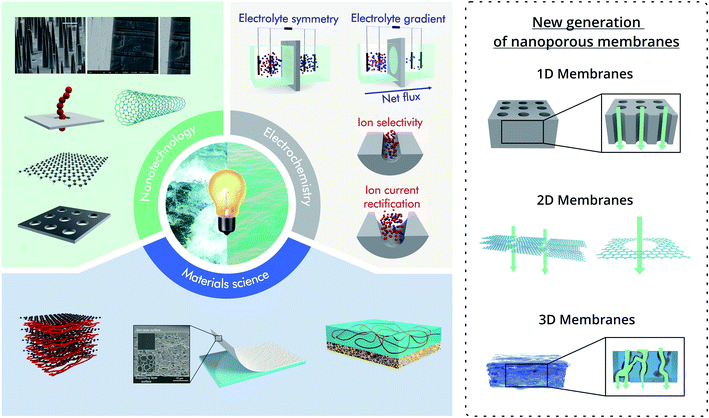 | ||
| Fig. 1 Scheme illustrating the combination of the knowledge from different areas such as nanotechnology, materials science, and electrochemistry with the aim to harvest salinity gradient energy. On the right, schematic examples of the different types of nanoporous membranes are shown. Scanning electron microscopy images in the nanotechnology section were adapted with permissions from ref. 38 and 63. Copyright © 2018 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim. Copyright © 2020 Published by Elsevier B.V. Membranes in the Materials science section were reproduced with permission from ref. 64 and 65. Copyright 2020, The Author(s). Published by Springer Nature. Copyright © 2020, Oxford University Press. | ||
This article presents an overview of the state-of-the-art of nanofluidic reverse electrodialysis (NRED) employing a new generation of nanoporous membranes. The next section introduces some basic terminology that will be employed throughout the review. Then, the main fundamental concepts about ion selectivity in charged nanoporous membranes and salinity gradient energy generation principles are presented. Sections 4 and 5 are focused on the analysis of the experimental set-ups and the various nanofabrication methods, respectively. The impact of different experimental variables on the performance of NRED devices is analyzed in Section 6, while the different scaled-up devices for NRED based on multi-channel, two-dimensional (2D), and three-dimensional (3D) membranes are introduced in Section 7. Finally, the review article finishes with two sections including the upcoming challenges, the conclusions, and perspectives related to this emerging field to take a step towards the evolution of these novel innovations at the lab-scale into technological platforms with favored features both in economic and environmental terms.
2 Basic definitions
To avoid ambiguities, this brief section introduces the main conventions used in this review to describe the different nanostructures. In all cases, the term nano is used for structures that contain at least one dimension in the nanometric range (1–100 nm). In the case of single-pore or low pore-density systems, the term “nanochannel” will refer to channels with a high aspect ratio (length ≫ aperture size) whereas the term “nanopores” will be used for “channels” with a low aspect ratio (length ∼ aperture size).59 Typical examples of nanochannels are those obtained in ion-track-etched membranes and anodic aluminum oxide (AAO). Typical examples of nanopores are pores obtained in atomically thin 2D membranes such as boron-nitride, SiN, or MoS2 (Fig. 1).In the case of up-scaled membranes (membranes with a high density of channels/pores), three major kinds of systems are addressed in this article: multi-channel membranes (or 1D membranes), 2D laminar membranes, and 3D membranes (Fig. 1). Multi-channel membranes refer to membranes containing a high density of discrete parallel oriented nanochannels such as the case of multi-channel track-etched and AAO membranes. 2D laminar membranes refer to ultrathin membranes of large lateral dimensions created by the stacking of nanosheets of materials such as MXene, graphene, or black phosphorus.60 While it is possible to create 2D membranes with a single discrete pore via nanofabrication techniques such as focused ion beam or electron beam (as shown in Fig. 1), in the case of up-scaled energy conversion systems, the laminar structure (stacked nanosheets) forming interstitial nanochannels is the most common 2D membrane design.61 Finally, 3D membranes refer to membranes consisting of micrometric networks with interconnected pores such as hydrogel-based membranes. The main aim of these definitions is to distinguish between the different mechanisms of ionic transport (Fig. 1). In the case of multi-channel and 3D membranes, the transport of ions is across the different channels and interconnected pores respectively, whereas in the case of 2D layered membranes the interstitial spaces between the nanosheets act as “lamellar channels” enabling the ion transport.43 Finally, the terminology nanoporous membrane is intended to encompass all the membranes discussed throughout this review, i.e. commonly thin ion-selective membranes (length ∼< 100 μm) with pore (or channel) size in the nanometric range.62
3 Osmotic energy conversion – fundamental concepts
3.1 Selectivity mechanism in charged nanoporous membranes
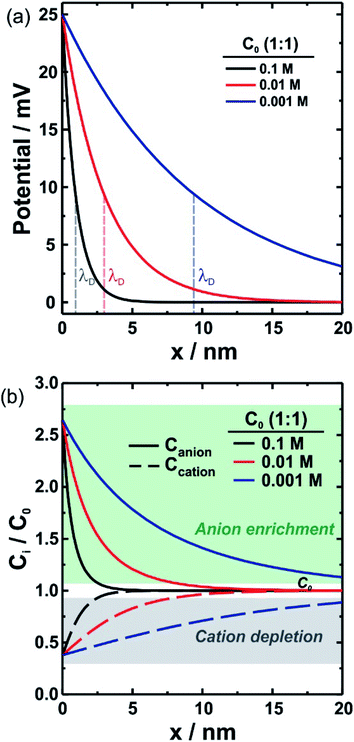
The immersion of a charged surface in an electrolyte solution promotes spatial ionic redistribution due to the influence of the surface electrostatic potential. The interface region in the solution is usually called the electrical double layer (EDL).66–68 As a result of the interactions between the ions and the surface electrostatic potential in the EDL, an enrichment of counter-ions (ions with the opposite charge type to the surface charge) and a depletion of co-ions (ions with the same charge type of the surface charge) is produced. Even though it is difficult to exactly determine the extension of the EDL, under certain conditions, it is possible to obtain an equation that accounts for the behavior of the surface electrostatic potential in terms of the distance to the surface. As an example, for low electrical potentials (<|25 mV|) and planar surfaces, the electrical potential expression can be reduced to the Debye–Hückel approximation (one-dimensional):69–71ψ(x) = ψ0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp[−κx] exp[−κx] | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1):
1):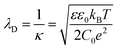 | (2) |
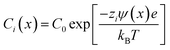 | (3) |
It is worth mentioning that these equations are only valid for flat surfaces and low surface electrostatic potential (i.e. low surface charge density) and when some of these assumptions are broken, the equations need to be modified. As an example, if cylindrical surface and Debye–Hückel approximation are assumed, a derivation in terms of the surface charge density can be obtained by applying sophisticated mathematical methods:70
| ψ(r) = σK0(κr)/[εκK1(κrc)] | (4) |
In contrast, if the geometry is maintained (flat surfaces) but now the surface electrostatic potential is higher than ca. 26 mV, the Gouy–Chapman expression becomes valid:70,72
| [exp(zeψ(x)/2kBT) − 1]/[exp(zeψ(x)/2kBT) + 1] = {[exp(zeψ0/2kBT) − 1]/[exp(zeψ0/2kBT) + 1]}exp[−κx] | (5) |
This equation reduces to eqn (1) when low surface electrostatic potential is considered. In comparison with eqn (1), for highly charged surfaces, the electrostatic potential predicted by eqn (5) displays a more pronounced diminution as x increases.70,71 While flat surfaces are still considered in the deduction of this equation, this could be valid in the case of SSN with a radius much higher than the Debye length.28
As can be seen in eqn (4) and (5), the expression complexity drastically increases as fewer assumptions are considered. In the case of nanocurved and highly charged (ψ0 > 26 mV) surfaces, as it is the case of several SSNs, numerical methods are usually needed to describe the ion concentration inside the channel.28,73 In this context, even though the Debye–Hückel approximation is only applicable for low surface potentials, from a qualitative perspective, the equation not only successfully describes the effects of electrolyte concentration and valence state but also enables easy understanding of the effect of the experimental variables on the electrostatic potential. For this enormous conceptual value, in this review, we usually refer to eqn (1) and equations derived from it. Further details on these models can be found in ref. 28 and 70.
The fact that λD represents the characteristic length of EDL denotes great relevance for ion transport processes across nanofluidic devices with sizes in the order of λD. Surface charges are expected to promote a non-negligible enrichment of counter-ions inside of the nanostructure leading to an increase in the counterion concentration in the channel which results in surface-charge-governed transport.30,74 While the relationship between the λD and channel size is the most used theoretical framework to explain the selectivity in channels with rc ∼ λD, a recent study has demonstrated that a more complete criterion of selectivity is provided by analyzing the Dukhin length (lDu).75lDu is defined as the ratio between the surface and bulk conductance and can be expressed in terms of the surface charge σ as:
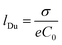 | (6) |
Consequently, the relationship between the lDu and the channel radius rc can be used as a reliable criterion of selectivity (or Dukhin number Du = (lDu/rc)). More in detail, when lDu/rc > 1, the system can display a selective behavior independent of the ratio λD/rc. Considering the topic addressed in this review, the analysis in terms of Du allows us to conclude that, similar to traditional ion-selective membranes, it is possible to achieve ion selectivity in membranes with larger nanopores (e.g. 10–100 nm).75 Finally, this ion-selective behavior arising from the sessile surface charges fulfills the prime requirement for acting as a nanofluidic RED (NRED) membrane and, therefore, allows the nanoporous membranes to become good candidates for osmotic energy conversion applications.
The slippage, another important phenomenon in nanochannels, is given by the friction of liquid/solid at the interface (for further details see ref. 72, 76 and 77). This phenomenon can have profound implications on electrical and diffusive transport and for this reason, it has been widely studied.78–81 The slippage can be characterized with a slip length b defined as the distance where the linear extrapolation of the velocity component vanishes which depends on the fluid viscosity and the friction coefficient of the surface.72,76,77 This parameter highly depends on the features of the surface such as roughness and the strength of the surface–liquid interaction. One of the most remarkable consequences of this phenomenon is related to the appearance of important values of zeta potentials even on surfaces with low charges.78,79 Regarding the focus of this review, the hydrodynamic slip has been highlighted as a phenomenon that can strongly enhance blue energy conversion in RED systems by reducing the solid–liquid viscous friction.82–84
3.2 Salinity gradient energy
The worldwide growing demand for energy and environmental problems caused by the burning of fossil fuels leads to increased research into new ways of sustainable energy generation.85 In this context, the salinity gradient energy (SGE) is perceived as a promising sustainable approach for electrical energy with great potential and availability.19,85–87 The fundamental concept of SGE comes from the production of electrical energy through the Gibbs free energy involved when two electrolyte solutions of different activities are mixed.88 The Gibbs free energy of mixing (ΔGmix) released in mixing processes between concentrated and diluted solutions is described by the following equation:19,52,89| ΔGmix = Gm − (Gc + Gd) | (7) |
| G = ∑niμi | (8) |
μi = μ0i + RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(γixi) ln(γixi) | (9) |
ΔGmix = ∑[Ci,mVmRT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(γi,mxi,m) − (Ci,cVcRT ln(γi,mxi,m) − (Ci,cVcRT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(γi,cxi,c) + Ci,dVdRT ln(γi,cxi,c) + Ci,dVdRT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(γi,dxi,d))] ln(γi,dxi,d))] | (10) |
Eqn (10) allows estimating the Gibbs free energy involved in the mixing process. For instance, ΔGmix is estimated to be around −1.5 MJ (negative magnitude indicates released energy) when mixing 1 m3 of river water (0.01 M NaCl) and 1 m3 of seawater (0.5 M NaCl).19 This process is irreversible and when two solutions are directly mixed, this energy is rapidly dissipated.91,92 From this perspective, the main goal of an SGE system is focused on controlling the mixing process in such a way that the energy involved could be harnessed and efficiently converted into electrical energy. As already mentioned, several methods have been reported to tackle this goal, e.g. RED, diffusion-osmotic, PRO, and capacitive mixing.91 Considering the characteristic of nanoporous membranes addressed in this review, the attention will be focused on the RED process and diffusion–osmotic mechanism.
3.3 Nanofluidic reverse electrodialysis (NRED)
In contrast to the conventional reverse electrodialysis, the NRED entails the “controlled” mixing employing nanoporous membranes rather than the conventional “dense” membranes containing sub-nanopores. The utilization of these nanoporous membranes for energy conversion has attracted special attention due to its technological potential in the energy production field ensured by the combination between ion selectivity and low resistance.93When a charged membrane that contains channels is exposed to an electrolyte solution, this will attract counterions while expelling co-ions due to the electrostatic interactions (Donnan exclusion) (see Section 3.1). Considering that the counterion concentration inside of the membrane is higher than those in the adjacent solution and the opposite occurs for the co-ion, a concentration gradient is established that promotes a flux of co-ions from the solution to the membrane and in the opposite direction for the counterions. However, the net flux of ions is null since this concentration gradient is counterbalanced due to the appearance of an electrical potential, the so-called Donnan potential ψD, which is given by:94–96
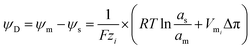 | (11) |
In the case of NRED, the method consists of exposing a membrane that contains charged nanochannels or nanopores to a concentration asymmetry, i.e. to electrolyte solutions with different concentrations at each side (Fig. 3). This fact establishes an ion flux across the membrane creating a transmembrane potential (Em) with three components:50,94,95,97,98
| Em = ψβs − ψαs = ψdiff + (ψ′′D − ψ′D) | (12) |
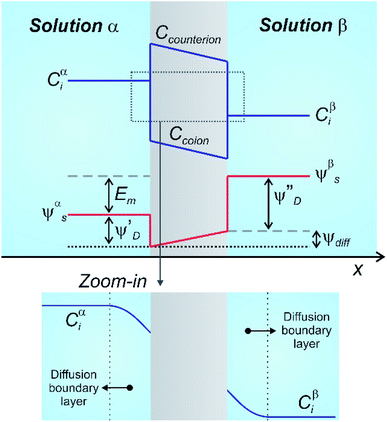 | ||
| Fig. 3 Schematic representation describing the concentration (C) and electrical potentials (ψ) involved when a charged membrane is placed separating a concentration gradient. The zoom-in illustrates the formation of diffusion boundary layers at both sides of the membrane/solution interfaces. More detailed approaches are available in ref. 94, 95 and 98. Em: membrane potential; subindex: i: i-ion; s: solution; D: Donnan; diff: diffusion. | ||
To derive a useful expression for Em and the experimental variables, the transference number ti is introduced which denotes the fraction of the current carried by the i-species (Ii):66
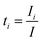 | (13) |
| ∑ti = 1 | (14) |
| t+ + t− = 1 | (15) |
The magnitude of Em depends on the asymmetry of charges at each side of the membrane which is related not only to the ion activities but also to the capability of the ion to be transported through the membrane:66,95,99
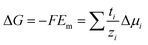 | (16) |
Considering the case of a monovalent salt:
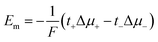 | (17) |
Introducing the expression for the chemical potentials,
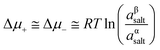 | (18) |
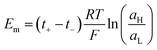 | (19) |
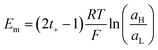 | (20) |
Therefore, exposing a perm-selective membrane to a concentration gradient gives rise to a transmembrane voltage difference (Nernstian) that depends on both the gradient magnitude as well as the membrane capability to transport counter-ions over co-ions. Furthermore, this equation depicts the possibility to estimate the transport number under the operative conditions, and therefore, to analyze the membrane selectivity by measuring Em.50,100 Note that this equation was derived neglecting the water transport. If the solvent transport was considered, the final equation would look like eqn (19) but the transport numbers would be apparent rather than the real values.95 Finally, it is worth mentioning that an equivalent equation can be derived via Teorell, Meyer, and Sievers theory (TMS theory) by employing eqn (12) as the starting point.97,99
Taking into account the existence of Em, the electrical potential generated in the nanochannels by the ionic current can be expressed as:101–103
| Vt = Em − IRc | (21) |
| Em = I × (R + CRload) | (22) |
One of the most important parameters to characterize the system performance in energy-conversion is power (P):
| P = I × Vt or P = I2 × Rload | (23) |
Combining eqn (22) and (23), the following useful expression for P in terms of Rload is obtained:101,104,105
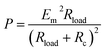 | (24) |
When Rload = Rc, the output power acquires the maximum value (Pmax):
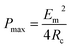 | (25) |
Applying eqn (21) for the case Vt = 0 yields:
 | (26) |
Finally, combining (24) and (18), Pmax can be expressed as:
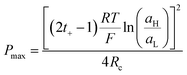 | (27) |
This equation has a high conceptual relevance since it denotes the need to achieve an adequate balance among the gradient concentration, the channel resistance, and the selectivity of the nanofluidic device for optimizing Pmax. In other words, a permselectivity membrane is not sufficient to obtain high Pmax values. For instance, Fig. 4 shows the effects on the power of variables such as the concentration gradient, membrane resistance, and selectivity. According to eqn (27), to increase the energy harvested, the increment and diminution of ion selectivity and membrane resistance are necessary since these parameters would enable more efficient mixing (Fig. 4(a) and (b)). In the case of the gradient, an increase of the difference of concentration between the high- and low-concentration reservoirs promotes an increase in the driving force of the SGE method and thus, an increment in the power (this trend is also evidenced in eqn (10)) (Fig. 4(c)). However, it is worth mentioning that this equation only considers the resistance due to the membrane but, in practice, additional resistances that affect (e.g. resistances from solution and diffusion boundary layers) the output power must be considered.107,108 For its part, variation in the reservoir concentrations can significantly affect the membrane selectivity, which would also generate a deviation from the power value predicted by eqn (27). These issues will be addressed in detail throughout the review.
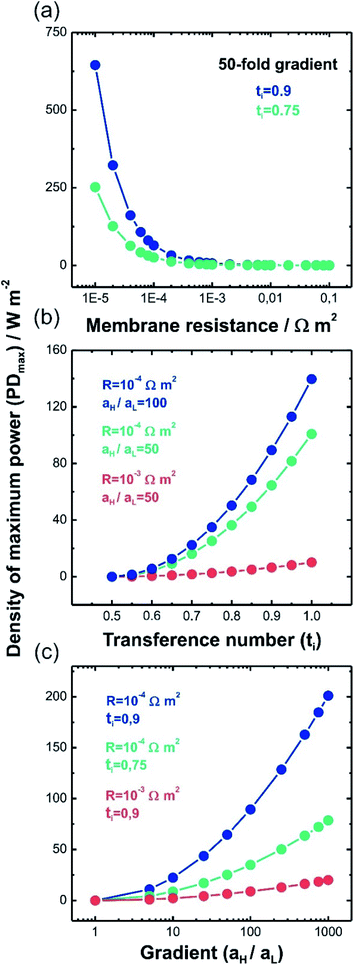 | ||
| Fig. 4 Density of maximum power (PDmax) predicted by eqn (27) as a function of (a) membrane resistance (R), (b) transference number and (c) gradient concentration (aH/aL) (T = 298 K). | ||
Another parameter with paramount relevance for SGE systems is the efficiency (η) of the energy-conversion system which was defined by Fair and Osterle as the energy recovered compared to the ΔGmix applied:109
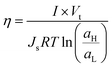 | (28) |
| Js = J+ + J− | (29) |
The current generated by the selective ion diffusion can in turn be expressed in terms of the fluxes of the cation and anion:
| I = zF(J+ − J−) | (30) |
As the cation transference number is the cation contribution to the current, it can be defined as follows:103
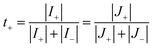 | (31) |
Considering that the maximum power is obtained when Rload = Rc and therefore, Vt = Em/2, the maximum efficiency (ηmax) can be expressed as:
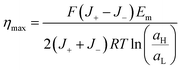 | (32) |
Combining eqn (32) with eqn (19) gives
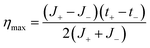 | (33) |
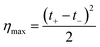 | (34) |
Finally, considering the definition of the transference number, eqn (34) can be rewritten:
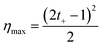 | (35) |
The maximum efficiency acquires values between 0 and 0.5 (or 0–50 when expressed in percentage value). Values around 0.5 can be obtained by maximizing the membrane selectivity, thus creating highly asymmetric ionic transport. This method for the efficiency calculation is an oversimplification since it does not consider other processes that contribute to the loss of efficiencies such as water transport and unutilized energy.110 However, as we will see, it is the most common way to estimate the efficiency in blue energy systems at the lab scale.
3.4 Diffusio-osmotic mechanism
As was pointed out in a pioneering study by Derjaguin,111 when a solid surface is exposed to a salinity gradient, an osmotic pressure gradient is generated in the diffusion layer yielding a diffusion-osmotic flow. In contrast to the NRED process (and RED), the diffusion–osmotic flow can be achieved even in membranes without ion permselectivity due to the interaction between the ions and the surface.11,77,112 For this reason, the diffusion–osmotic process is considered an intermediate between RED and PRO. More in detail, the gradient concentration promotes an interfacial osmotic pressure gradient in the first few nanometers from the surface that generates a water flux with a plug-like profile. The velocity of this flow (VDO) can be estimated with the following expression:46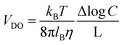 | (36) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) C is the concentration gradient, and L the pore length. If the surface contains a net charge density (σ) different from 0, this flow carries the excess of ions and, concomitantly, generates a diffusion–osmotic current (IDO) that obeys the following expression:46
C is the concentration gradient, and L the pore length. If the surface contains a net charge density (σ) different from 0, this flow carries the excess of ions and, concomitantly, generates a diffusion–osmotic current (IDO) that obeys the following expression:46| IDO = N2πrcσVDO | (37) |
4 SGE: experimental aspects
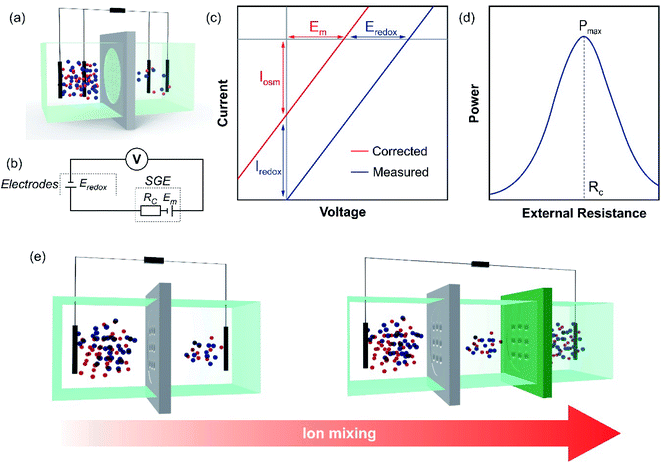
Fig. 5(a) shows a typical half-cell (or unit cell) used for NRED (or diffusion–osmotic) experiments at a laboratory scale. The nanoporous membrane is placed in a cell and separates two reservoirs filled with two electrolyte solutions of different activities (e.g. NaCl or KCl) and, to obtain the osmotic energy parameters, an arrangement of two or four electrodes is connected to a potentiostat or an external circuit with a load resistance (Fig. 5(b)). Typically, this kind of lab-scale experiment is performed by using a pair of Ag/AgCl electrodes. Taking into account that each electrode is immersed in a chloride-based solution with a different activity, the cell can be represented by the following scheme:66If Ag/AgCl electrodes are considered to be identical, a concentration cell is generated due to the voltage drop at the electrode surfaces. The potential magnitude of this concentration cell is Eredox:
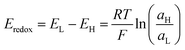 | (38) |
So, under these conditions, the open-circuit voltage (OCV) is given by:
| OCV = Em + Eredox | (39) |
In this way, the open-circuit voltage (OCV) or reversal voltage corresponds not only to the contribution provided by the membrane (i.e. Em) but also experiences an additional voltage drop due to Eredox. Therefore, to obtain pure osmotic energy contribution, Eredox must be subtracted. This aim can be accomplished by different methods. On the one hand, the voltage drops at the electrode surface can be prevented by working with Ag/AgCl electrodes with salt bridges and immersing both electrodes in the same electrolyte concentration, typically 3 M KCl.63,113,114 However, depending on the salt type used in the experiments, additional junction potentials must be considered.115 In long-time experiments, ion leakage from the salt bridge can change the electrolyte concentration in the reservoirs (especially in the low concentration reservoir) which produces a negative impact on the energy performance.51 On the other hand, if the experiments are carried out with Ag/AgCl electrodes without salt bridges, the Eredox contribution can be either directly estimated from eqn (38) or measured by replacing the ion-selective membrane with a non-selective membrane.101,116,117 With Eredox in hand, Iosm and Em are obtained applying the following expressions:116
| Iosm = ISC − Iredox = ISC − GEredox | (40) |
| Em = OCV − Eredox | (41) |
Typically, there are two classical routine SGE experiments and therefore, two common ways to obtain the SGE parameters: (a) I–V curves by scanning the transmembrane voltage employing a potentiostat (or an ammeter with a voltage source); (b) current–load resistance (I–R) and power–load resistance (P–R) curves. In the former method, as depicted in eqn (21), the response is characterized by a linear I–V curve shifted from the (0;0) point (Fig. 5(c)). From the intersection in the x and y-axis, OCV and ISC are obtained. Then, Em and Iosm are deduced by subtracting the contribution of the redox potentials (eqn (40) and (41), if applicable). Finally, it is possible to obtain Pmax, t+, and ηmax from eqn (26), (20), and (35), respectively.63 It is worth noting that in some systems, the I–V response can be slightly non-linear and the employment of eqn (26) could lead to little deviations in the Pmax estimation.118 In these cases, representing power vs. voltage (P–V) curves and obtaining Pmax graphically could be the best option. In the latter method, the extracted osmotic power is transferred to an external circuit with an electronic load (eqn (24)) (Fig. 5(d)). When Rload = Rc, the curve exhibits a maximum value corresponding to the maximum extracted output power.51,101 However, some authors have reported overestimation in the Pmax obtained by this method due to the difficulty in subtracting the redox contribution.116,119
To increase the voltage generated, different unit cells can be connected in series (tandem cells), or cation-selective and anion-selective membranes can be stacked alternately (full cells) separating concentrated and diluted solutions (Fig. 5(e)). In this regard, under ideal conditions, the purely osmotic open-circuit voltage linearly scales with the number (nm) of nanoporous membranes:52,104
| OCV = nmEm | (42) |
In this case, Em is the membrane potential of each cation and anion-selective membrane (considering the same permselectivity in both cases). Moreover, from a technological perspective, the use of full cells results in a promising alternative to maximize the energy extracted regarding the total volume of high- and low-concentration solutions (specific extractable energy) since, in contrast to half-cells, the mixing is due to the flux of both cations and anions.108 It is worth mentioning that, in practice, the scale-up is not linear due to different sources of energy losses such as additional resistances which lead to the need to optimize the architecture of the cell and electrodes.52,107,120–122 Finally, as it will be shown later, by employing full or tandem cells, several authors have demonstrated the possibility to switch on LEDs, calculators, and other electronic devices.53,123,124
Beyond the experimental aspect, it is possible to carry out a theoretical analysis of NRED performance by Poisson–Nernst–Planck and Navier–Stokes (PNP–NS) model-based simulations. The results based on the PNP–NS model have acquired great relevance regarding the influence of experimental variables such as length, size, electrolyte gradient, etc., either in single-pore or high-pore density systems. Details about PNP–NS simulations for single and multi-channel systems are addressed in ref. 125–130.
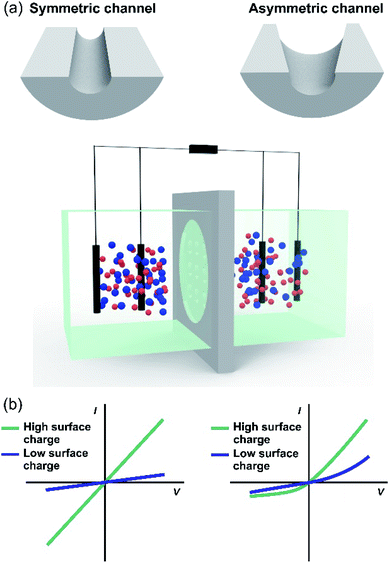
Although routine experiments related to energy conversion are performed under asymmetric electrolyte conditions, experiments in the presence of symmetric salt concentration are very common for characterizing the ion transport properties of the nanoporous membranes. In these cases, the membrane is placed in a two-half cell separating two reservoirs filled with two identical electrolyte solutions, and two or four-electrodes are connected to a potentiostat or picoammeter (with a voltage source) in a similar way to those used for the SGE experiments (Fig. 6(a)). Commonly, a cyclic linear sweep voltage program is applied, and simultaneously, the current is recorded. As the ions are the signal carriers, the response is often called the iontronic output. Under surface-charge governed transport, symmetric membranes display an ohmic behavior, i.e. a linear relationship between transmembrane current and voltage, with a surface charge-dependent conductance (slope of I–V curve) (Fig. 6(b)). On the other hand, when the ion-selective membrane is asymmetric either by the presence of asymmetrical channels or asymmetric modifications, the response is characterized by an ionic current rectifying behavior (diode-like behavior) (Fig. 6(c)).131 In other words, the platform displays a non-ohmic (non-linear) transport described by an enhanced current at a given voltage polarity. Moreover, the rectification efficiency is quantified employing the rectification ratio (or rectification factor) which is determined from the ratio between the current in the high and low conductance branches, respectively.132 Usually, the rectification ratio increases as the surface charge increases.133,134 As explained below, this kind of transport provides attractive features related to energy conversion applications.11,41,135
5 Nanofabrication methods
One of the major challenges behind the construction of platforms based on nanoporous membranes for energy applications is centered on the reproducible synthesis of the nanostructure. For this reason, researchers have made great efforts in the study and development of new ways for the controlled fabrication of nanoporous membranes from different materials. So far, the creation of membranes containing nanopores or nanochannels with size and density well-defined has been achieved by techniques involving ion, electron beams, and electrochemical methods. It should be noted that the synthesis protocols for ultrathin, two-dimensional (2D), and three-dimensional (3D) membranes, are very different. This section is a summary of drilling and synthesis methods employed in the design of nanoporous membranes.5.1 Multi-channel membranes – 1D membranes
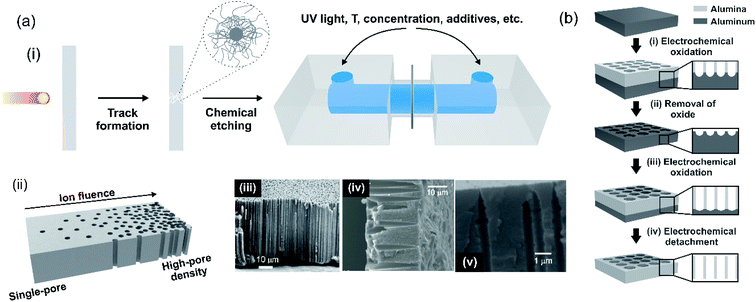 | ||
| Fig. 7 (a) (i) Scheme of ion-track-etching nanofabrication technique. (ii) Scheme illustrating the possibility of obtaining membranes with different pore densities by tuning the ion fluence. Scanning electron microscopy images of different membrane cross-sections containing channels with different geometries: (iii) cylindrical in polyimide (PI); (iv) conical in polycarbonate (PC) and (v) bullet in polyethylene terephthalate (PET). (b) Schematic illustration of the different steps involved in the fabrication of anodic aluminum oxide (AAO) membranes containing nanochannels by electrochemical anodization. Figure (a)(i) adapted with permissions from ref. 140. Copyright © 2012, Toimil-Molares. Figure (b) adapted with permissions from ref. 152. Copyright © 2004 American Chemical Society. Figure (a) (iii) was adapted with permissions from ref. 142. Copyright © 1996 Published by Elsevier B.V. Figure (a) (iv) was adapted with permissions from ref. 38. Copyright © 2018 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim. Figure (a) (v) was adapted with permissions from ref. 63. Copyright © 2020 Published by Elsevier B.V. | ||
Also, the final number of tracks per area unit can be adjusted during irradiation from a single ion up to 1012–1013 ions per cm2 (ion fluence) (Fig. 7(a)(ii)).140 This fact has important technological relevance since it makes possible the accurate control of the final channel number in a certain membrane area (pore density).
After irradiation, in a second step, each ion-track is transformed into a nanochannel by a selective chemical etching procedure.69,141 The selectivity of the track etching process is based on the radiation damage with pronounced changes in the chemical and physical properties compared to the non-irradiated bulk material. For track etching, the irradiated materials, such as PC or PET, are typically exposed to aqueous NaOH solutions whereas PI foils require NaOCl solutions with active Cl.142 The geometry and size of the final channels is controlled by choosing suitable etching conditions, e.g. increasing the time of etching results in larger channels or adding a surfactant to the etchant modifies the opening geometry of the nanochannels (Fig. 7(a)(iii)–(v)).34,36,143–148 For nanosized channels, the channel shape (cylindrical or conical) has a strong influence on the I–V curve, e.g. leading to a diode-like behavior. The geometry control thus has a significant effect on the performance of SGE devices based on track-etched nanochannels.
5.2 Single nanopores on 2D materials
5.3 2D laminar and ultrathin nanoporous membranes
The balance between ion selectivity and high conductance gave rise to 2D laminar and ultrathin membranes, which are a desirable feature for the development of the SGE platforms.57 2D laminar nanoporous membranes are typically obtained by stacking nanosheets, thus creating interstitial interlayer spaces that work as nanofluidic channels.61 Until now, 2D laminar nanoporous membranes have been created using various materials, such as carbides, nitrides,166 carbonitrides of early transition metals (MXene),167 graphene,123,168,169 black-phosphorus (phosphorene),170 boron nitride nanosheets,124 and kaolinite,171 among others.172There are at least two common methods for the creation of 2D laminar membranes: (a) vacuum filtration and (b) layer-by-layer (LbL) assembly. Membranes based on MXene, graphene, black phosphorus, and reconstructed kaolinite are usually obtained by vacuum filtration of a stable colloidal dispersion of the material that produces the assembly of the membrane (Fig. 8(a)).123,170,173 Subsequently, the material needs to be detached to form the free-standing membrane. In some cases, the preparation of the material dispersion requires some pretreatments. For instance, in the case of MXene, the starting solid often contains an Al layer in the phase. This is why a selective chemical etching (e.g. with HF) is required beforehand to replace the A-group layer from the Mn+1AXn phase with other terminal groups such as –OH, –O, or –F.174–177 In the case of graphene, the dispersion can be obtained either commercially or by exfoliation of graphite applying different protocols (modified Hummers' method).178
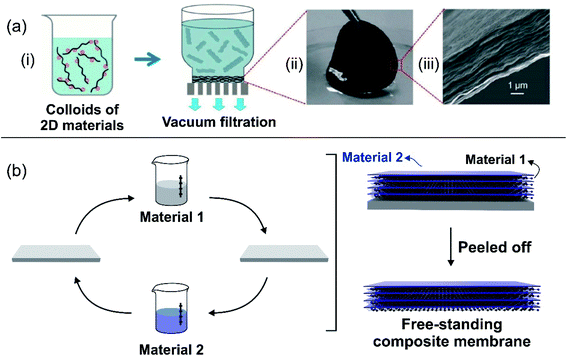 | ||
| Fig. 8 (a) Schematic illustration of a 2D-laminar membrane created by vacuum filtration. (ii) Picture and (iii) scanning electron microscopy image of graphene oxide membrane. (b) Schematic illustration of 2D-laminar membranes created by layer-by-layer assembly. Figure (a) adapted with permission from ref. 43. Copyright 2017 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim. | ||
The layer-by-layer method is attractive for the creation of composite 2D nanoporous membranes (Fig. 8(b)).179 For each component of the composite membrane a dispersion is prepared and then, a substrate (e.g. a glass slide) is alternately immersed in each dispersion. The assembly of the material onto the substrate surface during immersion is achieved by exploiting different intermolecular interactions such as electrostatic interaction or van der Waals forces. The thickness of the composite membrane is adjusted by the number of immersion cycles. After a given number of immersion cycles, the material is dried and the free-standing membrane is peeled off from the substrate.
5.4 3D nanoporous membranes
3D membranes consist of micrometric networks with interconnected pores, as in the case of hydrogel-based membranes. The generation of 3D nanoporous membranes is accomplished with a wide variety of reactions depending on the chemical nature of the network such as sulphonation reactions, non-solvent induced phase separation, photoinduced polymerizations of different precursor solutions, chemical oxidations (e.g. using 2,2,6,6-tetramethylpiperidine-1-oxyl radical as the catalyst), generation of agarose hydrogels, just to name a few.64,180–184 Conventionally, this kind of membranes can not only be created with a wide variety of thickness (in the micrometric range), pore sizes, and distribution but also can be used as a building block for the development of different asymmetric structures through its combination with other nanofluidic platforms such as AAO or track-etched foils. Also, in contrast with the previous systems, 3D nanoporous membranes containing interconnected nanopores enable the ion flow in various directions which promotes a decrease in the resistance.64 These concepts will be addressed in more detail in Section 7.2.6 Enhanced nanofluidic osmotic energy – the impact of structural and experimental variables on SGE performance
Recently, researchers have dedicated great efforts to determine the principal parameters that define the performance of SGE generators. Understanding the influence of the different structural and experimental variables on the energy conversion performance of nanofluidic-based platforms is crucial on the way to technological readiness. This section presents and discusses the effect of parameters such as nanochannel geometry (diameter, shape, length), pore density, and surface charge density, and experimental variables such as pH, concentration gradient, electrolyte nature, and temperature on the nanoporous membrane energy-conversion capability. Since many of these variables are often interconnected, the experimental situation is rather complex. Here we use a simplified scenario to provide guidelines for the creation and study of SGE platforms based on nanofluidic devices.6.1 Channel diameter
Nanochannel diameter is one of the most critical parameters and it has been the subject of study in several research papers. As an example, Tseng et al. theoretically studied the influence of diameter in a single cylindrical channel via Poisson–Nernst–Planck model simulations.126 Their results showed a remarkable effect of the channel dimension both on Em and Iosm. Conventionally, a lower channel dimension results in a better ionic selectivity due to the EDL overlapping that leads to a maximization of Em. Also, a small channel enables working with a high concentration gradient keeping the ion selectivity, which yields high ηmax values. However, the diminution of the channel diameter generates a decrease of Iosm (per channel) and therefore, a reduction of the power.63 This fact can be attributed to the decrease in the ion flux per channel caused by the critical decrease in the inner space.45,63Power maximization is a trade-off situation in which it is necessary to maximize ion selectivity and effective gradient but without compromising the Iosm values. Experimentally, this fact was evidenced by Feng et al. in their work focused on the NRED performance of a nanopore in a single-layer MoS2.45 When the pore size was lower than 10 nm, the pore displayed best Em values but it negatively impacted on Iosm. On the other hand, when the pore size was slightly higher than 10 nm, the pore displayed a high Iosm but with a decrease of Em. Finally, the estimated maximum output power density was 106 W m−2 for a pore diameter of 10 nm. A similar trend was also evidenced in bullet-shaped single nanochannels (Fig. 9(b)).63
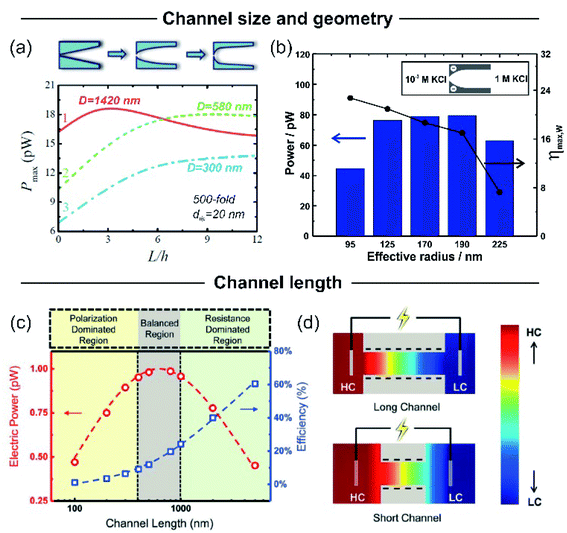 | ||
| Fig. 9 (a) Dependence of calculated output power with the channel curvature for channels with a tip diameter of 20 nm and variable base diameters (D). Reproduced with permission.128 Copyright 2018, Elsevier Ltd. All rights reserved. (b) Dependence of output power and maximum efficiency (ηmax,w) on the effective channel size for bullet-shaped polyethylene terephthalate nanochannels at pH 10 and a 1000-fold gradient. Reproduced with permission.63 Copyright, 2020 Elsevier Ltd. All rights reserved. (c) Dependence of the calculated electrical output power and efficiency on the channel length for a cylindrical channel with a diameter of 10 nm and a surface charge of −0.06 C m−2 and applying a 3000-fold concentration gradient. (d) Ion concentration distribution for two channels with different lengths. The ion concentration polarization effect is higher for shorter channels. HC and LC refer to high and low concentrations respectively. Reproduced with permission.193 Copyright 2017, WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim. | ||
In contrast to this behavior seen in single-pore membranes, the results obtained in multi-channel systems show that smaller pores can be a key to minimizing the detrimental effects of concentration polarization and thus, maximizing the output power in up-scaled membranes. This effect will be addressed in more detail in the following sections.182,185
Although pore diameters comparable to λD could be thought of as a limiting constraint, some authors have reported interesting counter-examples.119,186 Siria et al. reported the development of a single boron nitride nanotube with an inner radius of 40 nm that achieved an extracted power density of 4 kW m−2.46 The authors claim that the current generated by a diffusio-osmotic process has its origin in the osmotic pressure gradient in the interfacial diffusion layer due to the difference in salt concentration. They provide this reason why high performance was obtained with a nanotube appreciably larger than EDL.
6.2 Geometrical asymmetry
To overcome the trade-off between the size and the SGE parameters, membranes with channels of asymmetric geometry have been proposed. The membranes are typically 10–20 μm thick and have nanochannels with a small aperture (tip) of a few nanometers in diameter, whereas the other aperture has a diameter in the micrometer range (>100 nm). By employing this strategy, it is possible to decrease the channel resistance without considerably affecting ion selectivity.41,103,187,188 Furthermore, the disruption of the symmetry usually promotes the generation of devices with diode-like behavior which is advantageous since this non-ohmic behavior can suppress the back current and thus boost the output power by reducing the Joule heating loss.11,41,135 Within asymmetric geometry, the most studied systems contain bullet-shaped and conical nanochannels. Hsu et al. compared the performance of a channel with the same length, tip, and base diameter but different shapes using PNP simulations.128 The authors found that if the base diameter of the channel is not excessively large (<1400 nm), the bullet-shaped geometry achieved the best power values because its higher inner space leads to a significant enlargement of Iosm (Fig. 9(a)). In contrast, the trumpet geometry results in the lowest power value due to its low inner space, which yields the lowest Iosm values. According to the simulations, the efficiency (or selectivity) of the trumpet geometry yields best results whereas the bullet shape displays the worst values and the conical geometry has intermediate efficiency. In this regard, Laucirica et al. reported for the first time an experimental analysis on the performance of a PET membrane with a single bullet-shaped nanochannel as the SGE device (Fig. 9(b)).63 In a similar way to that observed in cylindrical channels, the channel size and the power obtained denoted a trade-off situation. On the one hand, the increment of tip and base diameter enabled higher Iosm values (if the ion selectivity was maintained) but produced a decrease of Em. Beyond this trend, the device with an optimized size displayed a high output power of 80 pW per channel by combining appropriate experimental conditions with this bullet-shaped geometry which exceeded the reported values in conical nanochannels of similar dimensions.516.3 Channel length
The decrease of the channel length is considered to produce an increment in Iosm (Rc diminution) with a loss of selectivity (Em diminution), setting another trade-off situation.126,127,189–192 To shed light on this problem, Cao et al. conducted a comprehensive analysis of the impact of the channel length on the energy-conversion performance.193 Employing PNP simulations, the authors found that the trade-off between the increment of Iosm and the decrease of Em resulted in an enhancement of the output power at low and moderate concentration gradient (<300-fold) as the channel length decreases. However, when the SGE experiment was carried out at high concentration gradients (>300-fold) an anomalous dependence between the output power and the channel length was evidenced (Fig. 9(c)). Increasing the concentration gradient causes a severe ion concentration polarization (ICP) in short nanochannels (<400 nm) that gives rise to a diminution in the effective concentration gradient. Thus, the real difference of transmembrane concentration (effective concentration gradient) is lower than the bulk concentration differences at each side (concentration gradient) (Fig. 9(d)). This fact induces a decrease in both Em and Iosm. Concomitantly, in discrepancy with the intuitive viewpoint, if the concentration gradient was higher than 300-fold, an excessive decrease in the channel length led to a drastic drop in the maximum power. Considering this scenario, the authors claim that a length in the range of 400–1000 nm is the best option when the concentration gradient is around 3000-fold. For channel lengths lower than 400 nm the behavior is controlled by ICP (polarization-dominated region) whereas for channel lengths larger than 1000 nm, the power decreases due to the high Rc values (resistance-dominated region) (Fig. 9(c)). This behavior was experimentally observed by Su et al. in AAO membranes.194 By varying the time of the second anodization step during the AAO membrane synthesis, the authors created membranes with a wide range of channel lengths for SGE studies. In agreement with the PNP simulations, they found that a significant decrease in the channel length led to a detriment in the osmotic power due to the ICP-induced decline in the effective concentration gradient. On the other hand, a significant increase in channel length led to lower osmotic power values due to the higher membrane resistance. According to the simulations, the relationship between Pmax and the channel length has a maximum value when the thickness of the membrane was about 8 μm. Additionally, these authors demonstrated that this trend is independent of the surface charge value and polarity.6.4 Pore-density
Beyond the studies on single-pore membranes with accurate control of the different structural parameters, to create SGE devices with potential technological applications, the scale-up to high-pore density membranes is a major challenge. Although initial experimental studies estimated the multi-channel device potential considering it a linear dependence of the single-pore power, several recent theoretical129,130,195 and experimental studies180 have reported important deviations from linearity. Yazda et al. reported a comprehensive experimental study about this topic by analyzing the energy conversion performance of a 2D composite membrane formed by silicon nitride and boron nitride (Fig. 10).196 Taking advantage of a novel nanopore fabrication technique called tip-controlled local breakdown, they were able to create membranes with different pore-to-pore spacing and subsequently, to evaluate the energy capabilities under the different conditions (Fig. 10(a)). The analysis of the results shows that the diminution in the interpore distance to values lower than ∼500 nm yields an abrupt drop in both the Em and Iosm which was ascribed to a probable interplay between the Dukhin length and concentration polarization (Fig. 10(b) and (c)). Therefore, in order to minimize the pore–pore interaction and maximize the power density, the authors found a value of 500 nm as the optimum pore-to-pore spacing (Fig. 10(d)). Wei Guo and coworkers thoroughly investigated the reasons behind the anomalous behavior in multi-channel membranes in comparison to the extrapolated single-pore systems by PNP simulations (Fig. 10(e)).106,197 They found that the power output achieved by a multi-channel system with pore densities lower than 106 pores per cm2 could be appropriately estimated through the linear dependence of the single-pore results. However, for pore densities higher than 106 pores cm−2 the pore–pore distance is drastically diminished and the pore–pore interaction cannot be neglected. In these cases, the high pore densities induce a strong ICP near the membrane in the low-concentration reservoir that produces an increment of the entering resistance and, concomitantly, hindered the osmotic energy capabilities (Fig. 10(e)). This rationalizes why the power values strongly deviate from the value obtained by linear estimation from single-pore systems (Fig. 10(f)).46,198 In addition, several studies have shown that the ICP effect in multi-channel systems is lower as the channel diameter decreases due to the diminution in the ion flux per pore for smaller channels and the concomitant mitigation in the ICP (Fig. 10(g)).106,182,185 For this reason, the use of smaller nanochannels can be crucial for the development of up-scaled membranes. Furthermore, as described in the following sections, the use of heterogeneous membranes has been widely employed as an approach to reduce the mechanisms that vanish the output power harvested in membranes with high pore density. Despite the considerable advances in the last few years, the mitigation of the effects arising from pore–pore interaction in high-pore density membranes remains a major challenge in this area (see Section 8.1).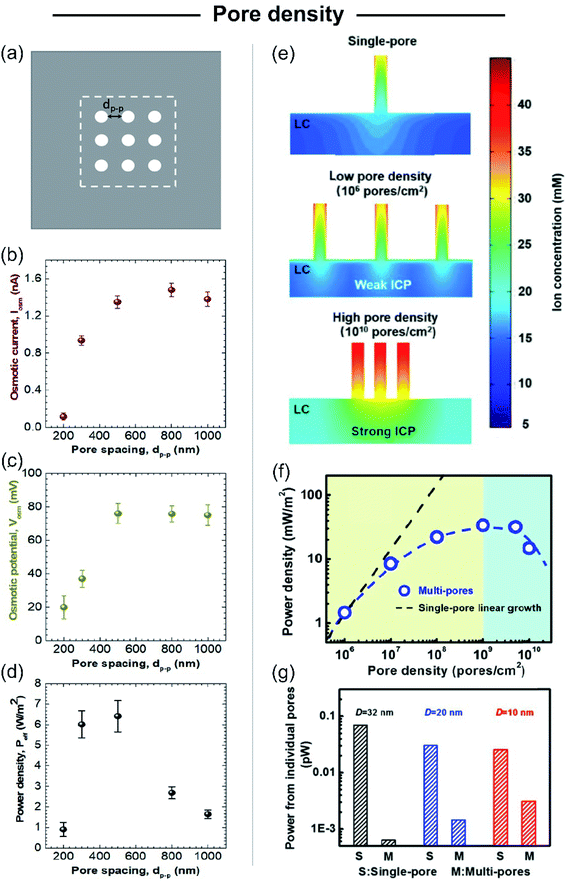 | ||
| Fig. 10 (a) Scheme illustrating the system employed for studying the effect of pore spacing (dp–p). The dashed box represents the working area used for maximum power density calculation. (b) Osmotic current (Iosm), (c) osmotic potential (or membrane potential, Em) and (d) maximum power density in terms of the pore spacing. Adapted with permission.196 Copyright 2021, American Chemical Society. (e) High-pore density membranes lead to strong ion concentration polarization (ICP). (LC refers to the low concentration reservoir). (f) Non-linear relationship between pore-density and output power. Power density vs. pore density curve was obtained by modeling cylindrical channels with length 60 nm, diameter 32 nm, surface charge density −0.06 C m−2, and a 10-fold gradient. (g) Power from individual pores for different single-pore (S) and multi-channel (M) systems containing channels with different diameters (D). Reproduced with permission.106 Copyright 2018, SIOC, CAS, Shanghai, & WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim. | ||
6.5 Surface charge density and location
The modulation of surface charge density is one of the most widely used strategies to experimentally improve the SGE conversion performance. There are at least two common approaches for adjusting the surface charge: (a) the control of experimental conditions such as pH or light; and (b) the attachment of different charged building blocks onto the channel surface.In a different approach, some materials offer the opportunity to modulate the surface charge density via a non-invasive stimulus, such as light. For instance, Graf et al. demonstrated an increase in the energy-conversion properties of MoS2 nanopores via light irradiation.201 This fact was ascribed to the light-induced increment in the surface charge of the pores. Similar strategies have been reported in 2D MXene membranes and TiO2/C3N4 heterojunction nanotubes.202,203 These examples illustrate the possibility to combine solar energy and SGE with a relatively simple strategy.
Beyond the importance of surface charge magnitude and sign, the location of charges also acquires a crucial role. For instance, a recent study showed that the immobilization of a polyelectrolyte layer not only on the walls of the channels but also on the outer walls of the membrane represents a simple approach to enhance the power output.188,207 On the other hand, the creation of systems with a distribution of net charges within the entire volume of the nanochannel interior (space charge) rather than just on the nanochannel walls (surface charge) has demonstrated to be a simple way to improve the SGE performance.65,118,208
In the last few years, asymmetric modifications producing heterogeneous membranes composed of two different monolayer porous membranes have been used as an essential strategy to boost the power in NRED systems.209,210 In 2019, Wei Guo and coworkers carried out a PNP-based study on the fundamental aspects of heterogeneous membranes as osmotic nanogenerators.211 In contrast to homogeneously charged nanofluidic devices, they demonstrated that the existence of a heterojunction suppresses the ICP phenomenon without compromising the ion selectivity. The effective concentration gradient does not vanish, and therefore, the Iosm and the extracted power increase. The analysis also includes the influence of the structural parameters of the heterogeneous region such as diameter and length. By employing a heterogeneous region with a small pore diameter (<20 nm), the ICP effect is overcome but a drastic reduction in the overall ion selectivity was also observed. These results suggest that it is indeed possible to boost the power exhibited by introducing a heterojunction region and to obtain an optimal balance between ICP suppression and high ion selectivity. For this, the optimization of the length and diameter of the heterogeneous region plays a crucial role. On the other hand, the disruption of the symmetry by introducing an asymmetric modification enables obtaining devices with diode-like behavior. This characteristic positively impacts the osmotic energy performance (see Section 6.2).11
6.6 Concentration gradient
Concentration gradient is one of the experimental variables that more critically impact the SGE generation. Typically, an increment in the concentration gradient causes a boost in the output maximum power since it generates a rise in both the Iosm and Em (Fig. 11(a)).45,51,63,114 However, in some cases, this relationship is not completely fulfilled and an excessive increment in the difference of transmembrane concentration can be counterproductive in the power exhibited. For a fixed diameter and pore-density, the concentration gradient has strong effects on the obtained power. On the one hand, the increment of the concentration gradient directly increases the power as it produces a richer free energy source from a thermodynamic point of view (eqn (20)). However, a high concentration gradient requires that one side of the membrane is exposed to a high electrolyte concentration, which concomitantly produces a loss of ion selectivity due to the efficient screening of surface charges (see the relationship between Debye length and salt concentration in eqn (2)).102,117,126,212 Considering eqn (20), this fact produces a decline in Em due to the diminution of counter-ion transference number. On the other hand, if the electrolyte concentration in the diluted reservoir is excessively low, a similar detriment in the output power can occur due to the diminution of t+, but in this case, this effect is attributed to the diminution in the surface charge caused by the regulation charge effect at low electrolyte concentration.190,213,214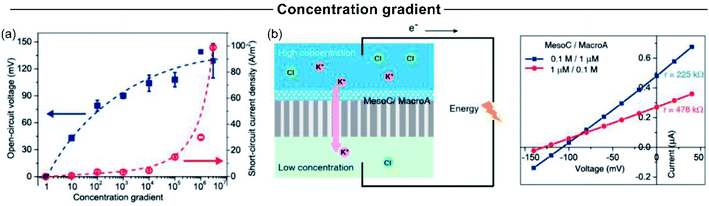 | ||
| Fig. 11 (a) Influence of concentration gradient magnitude on the open-circuit voltage and osmotic current. (b) Influence of concentration gradient directionality on the produced osmotic power by asymmetrically modified membranes. Reproduced with permission.219 Copyright 2014, American Chemical Society. | ||
For asymmetric channels, also the directionality of the gradient is important; i.e. at which side of the nanoporous membrane the highly concentrated and diluted solutions are placed (Fig. 11(b)).50,215,216 Supported by PNP simulations in geometrically asymmetric nanochannels, different authors showed a better energy-conversion performance when the diffusion flux was established from base-to-tip instead of tip-to-base which means that, to achieve the best output power and efficiency, placing the concentrated solution in the base side and the diluted solution in the tip side is convenient.51,103,105 The reason behind this behavior is ascribed to the increase (decrease) of the selectivity when the tip side was exposed to the diluted (concentrated) solution since the ion-selective mechanism in asymmetric channels stems from the tip region.217 However, when the asymmetry is provided by targeted surface modification, instead, anticipating which will be the best arrangement is more difficult. In these experiments, the system is usually tested in both configurations (Fig. 11(b)).64,218,219
6.7 Electrolyte nature
In addition to the concentration (i.e. activity) gradient, Cao et al. performed a comprehensive analysis of how the electrolyte nature impacts the performance of an SGE device based on a single conical PI nanochannel.220 Combining experimental results with PNP simulations, the authors showed that the net diffusion current (Iosm) is dominated not only by the ion-selectivity of the nanoporous membrane which favored the counter-ion flux but also by the inherent different diffusive properties of counter-ions compared with the co-ions of a given compound. To boost output power and efficiency, these two mechanisms must act synergistically.213Thus, the power in a cation-selective nanochannel can be increased by selecting KF instead of LiCl as the higher inherent diffusion of K+ in comparison to F− (DK+ > DF−) and the cation flux favored due to the cation-selective membrane would have a collaborative effect. For the case of an anion-selective membrane, the use of LiCl instead of KF is recommended since the higher inherent diffusion of Cl− in comparison to Li+ (DCl− > DLi+) and the anion flux favored due to the anion-selective nanoporous membrane would work synergistically.
In the case of sub-nanopore membranes, both size and diffusivity of hydrated and dehydrated ion sizes need to be considered.221–223 For example, for nanoporous membranes based on metal–organic frameworks (MOF) with pore sizes around 6–7 Å it was shown that counter-ions with a size lower than the pore size of the MOF are able to pass through the MOF porosity yielding higher ion fluxes and selectivity.224 Consistently, the transport across the porous MOF in the case of counter-ions with larger hydrated sizes is more restricted which leads to a detriment in the power capabilities. Quantitative results of different upscaled MOF-based membranes will be addressed in more detail in Section 7.2.
6.8 Temperature
Temperature is a relevant factor in the NRED performance since it directly affects the ion diffusion coefficients. In principle, the NRED experiment can be carried out both under isothermal and asymmetrical temperature conditions (i.e. the solution temperature at each side of the membrane being different). Until now, most experiments have been performed under isothermal conditions, where usually the Pmax is enhanced as the reservoir temperature increases due to the maximization of both Iosm and Em (see dependence of Em on T in eqn (20)).126,225,226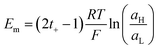 | (43) |
Otherwise, the ηmax is practically not modified as both diffusion coefficients (counter-ion and co-ion) are modified similarly and, therefore, the transport numbers remain almost unchanged.126,225 However, other temperature effects rather than that directly expressed in eqn (20) could arise. For some materials, temperature-induced changes in the surface charge which also cause variation in ηmax have been reported.175,227,228 As an example, on silica surfaces, an excessive increase in the temperature can result in a drastic diminution in Em and power explained by a reduction in the effective surface charge density owing to the formation of hydrophobic patches that mask the mesoporous surface.227
An asymmetric temperature configuration in NRED was addressed in detail by Liu and coworkers in their studies based on numerical simulations in cylindrical nanochannels.225,229 The effect of the temperature gradient was evaluated as a function of the temperature difference and the gradient direction, denoted as positive temperature difference (PTD) when the low-temperature reservoir coincides with the low concentration reservoir and as negative temperature difference (NTD) when the low-temperature reservoir coincides with the high concentration reservoir (Fig. 12(a)). The authors found that both NTD and PTD enable an increment in Iosm compared to the isothermal condition (considering the low temperature of the asymmetric experiment) since the electrical resistance depends on the average salt temperature. Nevertheless, while the NTD caused an increment in the selectivity and therefore, in Em, the PTD produced a detriment in this parameter. This fact produced a boost in the extracted power for the NTD configuration but, in contrast, a trade-off situation for the PTD (Fig. 12(b) and (c)). The authors argued that in the NTD situation the diffusion coefficients are enhanced along the osmotic–diffusion direction owing to the temperature impact and thus, the ion concentration inside of the channel is diminished and the selectivity maximized. Also, in the NTD case, the concentration in the channel exit in the low concentration reservoir is diminished due to the effect of the temperature on the diffusion coefficients which suppresses the ICP effect enabling the best Pmax (Fig. 12(d)) to be obtained. Considering these results, this configuration can acquire special relevance for avoiding the ICP promoted by the pore–pore interaction in multi-channel membranes.230
 | ||
| Fig. 12 (a) Different experimental configurations for temperature-dependent experiments of energy conversion. HC and LC refer to high and low concentration reservoirs respectively. (b) Electrical power displayed applying a 1000-fold concentration gradient at different temperature configurations. (c) Influence of the asymmetric temperature directionality on the power ratio compared with the isothermal condition (enhancement factor) in a cylindrical nanopore of diameter 20 nm, length 50 nm, surface charge density −0.05 C m−2. (d) Ion concentration profiles for different temperature configurations. A negative temperature gradient (NTD) leads to a diminution of the ion concentration polarization. Reproduced from ref. 229 with permission. Copyright © 2019, Oxford University Press. | ||
These results suggest that an increment in the osmotic energy can be achieved by simultaneously combining temperature and concentration gradients. Thus, the thermo-osmotic energy conversion obtained from the utilization of natural water sources (e.g. river and seawater) and low-grade heat waste could be a key for expanding the boundaries of NRED and thus, to widely exceed the commercial benchmark.231 Furthermore, low-grade heat waste can be harnessed for the thermal regeneration of low and concentrated solution giving rise to a type of RED in a closed-loop called RED heat engine.232
7 Towards the construction of NRED platforms with technological applications
The fundamental insights for the optimization of an NRED device have been introduced in previous sections, presenting results on either single-pore membranes (or low-pore density) experiments or PNP simulations. Nevertheless, with the purpose of producing real NRED devices, the scaling-up from single-pore to multi-channel is a crucial issue. Unfortunately, this is not a trivial challenge due to the hindered Pmax caused by the pore–pore interactions (see Section 6.4).106 Furthermore, the NRED applicability would depend on the properties of the available water sources. As an example, from its conception, the RED system was usually intended to be operated with river water (∼0.01 M) and seawater (∼0.5 M) which not only establishes a specific gradient magnitude (∼50-fold gradient) but also fixes other experimental variables such as the pH and electrolyte nature. In the last few years, the opportunity to use different water sources such as saline industrial waste or brine solutions as salinity gradient power resources has gained impetus due to their benefits in terms of power, environmental impact, and versatility.26 Also, as we will see, all the results were obtained employing millimeter working areas which is not a realistic condition (see Section 8.1). For the construction of NRED platforms with technological applications, these aspects have to be considered. This section presents strategies reported by different researchers that enable them to tackle the aforementioned challenges. For ease of reading, this section is subdivided into two parts introducing the following systems: (a) two-dimensional (2D) and other ultrathin membranes, and (b) multi-channel and three-dimensional (3D) materials (see Fig. 1).7.1 2D-materials based and ultrathin membranes for the development of SGE nanodevices
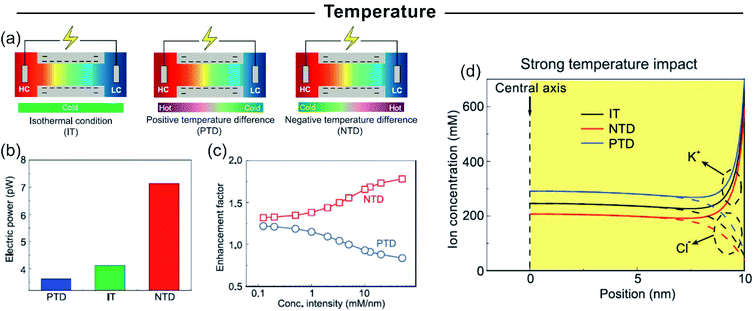
Up-scaled 2D membranes usually involve 2D-laminar membranes. Well-known examples of these materials for developing SGE devices are graphene,123,168,233 hexagonal boron nitride, carbon nitride,166 MXene,167 molybdenum disulfide,172 among others.116,171,234 In the case of 2D layered membranes the interstitial spaces among the nanosheets act as “lamellar channels” enabling ion transport. As previously explained, the combination of ultrathin membranes and highly charged “lamellar channels” can be a key in the development of highly efficient membranes for osmotic energy conversion due to their intrinsic high ion selectivity and lower resistance.113,235 In this section, some of those results obtained in up-scale 2D-based membranes are summarized.Ji et al. created NRED stacks by alternating negatively and positively charged 2D graphene oxide membranes created by flow-induced self-assembly and subsequent thermal stabilization (Fig. 13(a)).123 Due to the natural negative charge of graphene oxide, in the case of positive 2D membrane construction, the graphene oxide nanosheets were previously functionalized to form positively charged imidazolium groups. The ion selectivity of both membrane types in combination with the low resistance to the ion fluxes provides an output power density of 0.77 W m−2 per NRED stack applying a concentration gradient of 50-fold (simulated seawater and river water system) (Fig. 13(b) and (c)). Based on their platform, the authors were able to harvest osmotic energy from different water sources such as acid rain, industrial wastewater, brine, and urine which extends the applicability of this NRED system. Finally, the output voltage of the system reached 2.7 V by stacking 13 membrane pairs. It was demonstrated that this is sufficient to operate different electronic devices such as a calculator and light-emitting diodes (LEDs) (Fig. 13(d)).
 | ||
| Fig. 13 (a) Scheme of the experimental set-up of nanofluidic reverse electrodialysis stacks based on negative and positive graphene oxide (n-GO and p-GO) membranes. (b) The iontronic output under different directionalities is shown too. HC – high concentration reservoir – denotes an aqueous solution of 0.5 M NaCl and LC – low concentration reservoir – corresponds to an aqueous solution of 0.01 M NaCl. (c) Current density (black) and output power (blue) in terms of external resistance. The curve displayed a maximum at P ∼ 0.8 W m−2. (d) Schematic cell and dependence of voltage for the different number of nanofluidic reverse electrodialysis stack units (50-fold gradient). Tandem graphene oxide-based nanofluidic reverse electrodialysis systems can power an LED. Reproduced with permission.123 Copyright 2016, WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim. | ||
One of the most employed strategies to decrease the membrane resistance and increase the ion selectivity is the appropriate functionalization of the membrane. In the case of 2D-layered membranes, the creation of hybrid membranes by assembling different materials has become an attractive option.236–238 Wu et al. reported the construction of a composite membrane formed by graphene oxide and cellulose nanofibers (GO/CNFs).228 Under optimized conditions and applying a concentration gradient of 50-fold (mimicking seawater/river water), the system exhibited an output power density of 4.19 W m2 exceeding results obtained with isolated cellulose nanofibers and graphene oxide. This enhancement was ascribed to larger interlayer distances that allow fast ion transport and high transmembrane flux but without losing selectivity due to the space charge introduced by CNFs. Additionally, these authors studied the osmotic energy performance in terms of temperature. When increasing the temperature from 298 to 323 K, the output power was boosted due to the rise of both ion mobility and negative surface charge density. However, above 323 K the output power decreased owing to the formation of so-called nanopancake-like gas layers that shielded the charged zone. A similar temperature-dependence was evidenced in a previous work carried out on silica nanochannels.227
More recently, Zhu et al. introduced the first up-scaled 2D-membrane based on MoS2 for energy conversion purposes.172 The main difficulty in creating large areas of MoS2 2D-membranes comes from the low strength and stability of the stacked membrane. However, by combining MoS2 nanosheets with cellulose nanofibers (CNFs), the authors demonstrated a MoS2 lamellar nanoporous membrane with high conductivity, high ion selectivity, good mechanical strength, and stability in aqueous media. The nanocomposite membrane was created by vacuum filtration of a dispersion containing both components, the CNFs and MoS2 nanosheets. The energy conversion performance was studied for CNFs/MoS2 nanoporous membranes containing different amounts of CNFs and MoS2 phases. The increase in CNF concentration boosted the ion selectivity due to a larger amount of surface charges, but an excessive increment in the amount of this component yielded a detriment in the ion flux because of the physical sterical hindrance. For its part, the employment of MoS2 in the metallic phase (M-MoS2) rather than in the semiconducting phase enables enhancement of the ion flux and selectivity due to the high electron density of M-MoS2. Therefore, by using MoS2 in the metallic phase and optimizing the weight content of CNFs to 8%, the system displays PDmax ∼ 5.2 W m−2 applying an electrolyte gradient mimicking the natural seawater/river water system. Furthermore, using natural seawater from the China East Sea and river water, a PDmax of around 6.7 W m−2 was achieved which exceeds the commercial ion-exchange membranes. Notably, the final response was independent of the pH which opens the door for the utilization of different water sources such as ultra-acidic or alkaline wastes.
In the last few years, MXene compounds have emerged as a promising material for the construction of 2D-membranes with applications in nanoosmotic generators.239 These materials are based on the chemical formula Mn+1XnTx where M is an early transition metal (e.g. Ti, Cr, Mo, etc.), X is carbon and/or nitride and T is the terminal group (typically –O, –OH, or –F). MXene compounds are usually synthesized by selective etching of the A-group layer in the Mn+1AXn (MAX) phase.53,240,241 These terminal groups provide the surface charge to the MXene nanosheets and contribute to the interplanar spacing. One of the seminal articles on the MXene-based 2D layered membranes for NRED was published by Wang and coworkers in 2019.175 The authors constructed lamellar Ti3C2Tx membranes via the etching of Al from Ti3AlC2 followed by the assembly of the Ti3C2Tx dispersion by vacuum-assisted filtration (Fig. 14(a)). The resultant device exhibited a highly charged state at alkaline pH that, in combination with the low membrane resistance, enabled them to harvest an output power of 21 W m−2 and maximum efficiency of 40% applying a 1000-fold concentration gradient at room temperature (Fig. 14(b)). Furthermore, the increment in the temperature allowed maximizing the ion mobilities and the surface charge yielding a PDmax of 54 W m−2 (Fig. 14(c)).
 | ||
| Fig. 14 (a) Scheme of the Ti3C2Tx MXene membrane and the experimental set-up. (b) Output power density and the maximum efficiency extracted for different concentration gradients. (c) Power density as a function of the temperature. Adapted with permission.175 Copyright 2019, American Chemical Society. (d) Schematic representation of Ti3C2Tx MXene/aramid nanofiber (ANF) membrane structure (MXene/ANF). (e) Power density obtained for the composite membrane with different ANF contents. (f) Power density obtained for different pH values. Reproduced with permission.208 Copyright 2019, The Author(s). Published by Springer Nature. | ||
Exploiting the same material, Zhang et al. built a composite membrane based on Ti3C2Tx MXene and aramid nanofibers (MXene/ANFs) (Fig. 14(d)).208 The aramid nanofibers not only offered negatively charged groups but also enlarged the interlayer channel and acted as an interlocking agent to connect the nanosheets by hydrogen bonding. The aramid nanofiber content on the composite membrane had to be optimized since an excessive amount reduced the ion flux due to partial blocking of the 2D channels (Fig. 14(e)). Thus, under optimized conditions, these authors reported a PDmax of 4.1 W m−2 by using seawater from the Mediterranean Sea and river water from the Elbe River as gradient sources. Additional theoretical and experimental results showed that the good performance is explained not only by the increment of surface charge (and interlayer channels) but also by the spatial distribution (“space charge”) of charges offered by aramid nanofibers (Fig. 14(f)).
Recently, the development of a bio-inspired layer-by-layer assembled nanocomposite membrane (ABN) based on aramid nanofibers (ANFs) and boron nitride nanosheets (BNn) was reported.124 The system was created by the layer-by-layer deposition of aramid nanofibers and boron nitride nanosheets onto a PDDA-pretreated glass. This revealed remarkable mechanical properties with a tensile strength of 370 MPa and chemical stability in a wide range of pH and temperature. The negative charge of ABN made it possible to use it as an electrical nanogenerator yielding an osmotic Pmax density of 94 mW m−2 (without subtracting redox contribution PDmax ∼ 600 mW m−2) when applying a gradient of artificial seawater and river water. This result exceeds values obtained by other electrokinetic energy conversion methods.242 Also, an NRED system constructed with 10 tandem-connected osmotic cells was able to supply electronic devices with a liquid crystal display and the ABN-based membrane was able to act as a nanopower generator even with organic solvents.243 Interestingly, these results were obtained using an effective area of 3.14 mm2 but, when the effective area was decreased to 0.03 mm2, Pmax density was boosted to 5.9 W m−2 (without subtracting redox contribution). This finding suggests a non-linear behavior of the response in terms of the effective areas. For this reason, the article highlights the importance to perform the NRED experiments under conditions that emulate practical applications. The trade-off between the output power and working area was also evidenced by Chen et al. in the study of the energy conversion performance of a nanocomposite membrane based on aramid nanofibers and graphene oxide.238
7.2 3D-materials and other multi-channel membranes for the development of SGE nanodevices
With the purpose of developing platforms with technological applications, the scientific community has made considerable efforts during recent years to achieve an efficient scale-up to multi-channel membranes. The employment of 3D materials has been proposed as a simple way to obtain membranes with low cost and easy scalability acting as efficient SGE devices.65,135,184,244,245 The combination of interconnected 3D nanostructured networks together with the high surface and space charge leading to high conductance and selectivity has been identified as determining factors.246 In the last year, several proofs-of-concept have been introduced in the synthesis, characterization, and energy conversion testing of these materials. Zhang et al. introduced an organic heterogeneous membrane constructed by the integration of a functional polyelectrolyte hydrogel based on polystyrene sulfonate (PSS) on a porous aramid nanofiber (ANF) membrane via the sequential blade-casting method (210 μm-thick) (Fig. 15(a)).64 The chemical, electrostatic, and structural asymmetries resulted in a rectifying behavior with surface-charge-governed ion conductance below 0.1 M KCl. Furthermore, the enhancement of ion diffusion caused by a widely charged 3D hydrogel network added to the high cation selectivity provided by negative groups of PSS and ANF, and the advantages of interfacial design allowed it to act as an efficient energy nanogenerator. In order to obtain the best performance, both the gradient direction as well as the PSS content in the hybrid membrane were optimized. On the one hand, the results evidenced an increment in the power by establishing the ion diffusion direction from the ANF membrane to the PSS hydrogel (forward gradient) (Fig. 15(b) and (c)). On the other hand, an increment of PSS content up to 7% wt led to a boost in the power due to the increment in the surface charge (Fig. 15(d)). Additional increments of PSS are counterproductive owing to the increase of steric hindrance and concomitantly, a decrease in the ion flux. Finally, under optimized conditions, the device displayed a Pmax density of ∼5.06 W m−2 by mixing natural seawater and river water (∼130-fold) exceeding the commercialization benchmark (Fig. 15(e)). This work demonstrated the technological potential of heterogeneous membranes based on 3D polyelectrolyte hydrogels as SGE platforms.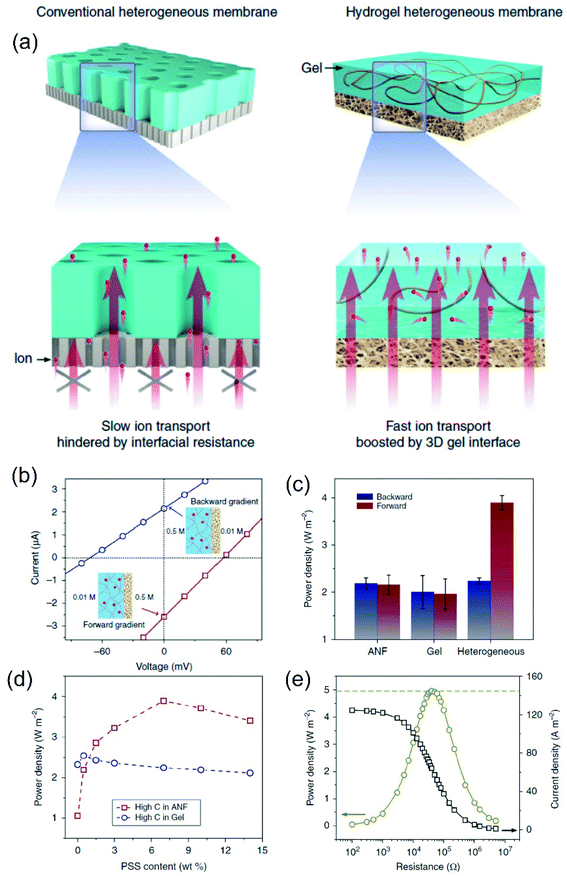 | ||
| Fig. 15 (a) Scheme of hydrogel heterogeneous membrane structure constituted by a polystyrene sulfonate (PSS) film onto a porous aramid nanofiber membrane (ANF). The 3D gel interface enabled fast ion transport regarding the conventional heterogeneous membrane structure. (b) I–V curves applying a 50-fold gradient under different directionalities. (c) Power density for the hybrid membrane and the isolated building blocks in both gradient directions. (d) Power density vs. the PSS content. The graph depicts the trade-off between the increment of surface charge and the increment of steric hindrance. (e) Power density and current density in terms of load resistance applying a gradient of natural seawater and river water (∼130-fold). Reproduced with permission.64 Copyright 2020, The Author(s). Published by Springer Nature. | ||
Recently, nanoporous membranes containing metal–organic frameworks (MOFs) or covalent organic frameworks (COFs) have emerged as an attractive approach due to the exceptional properties of these materials such as their distribution of ordered sub-nanochannels, the tailorable surface properties, the high surface area, and relatively straightforward chemical synthesis.223,247,248 In this regard, Zhao et al. introduced an inorganic–organic composite membrane that consisted of the integration of MOF nanosheets into a heterogeneous organic membrane.249 This ion-selective membrane was created in a two-step process. First, a sulfonated polysulfone (SPSF) solution was cast and, subsequently, dried on a Si wafer. Then, a dispersion of sulfonated poly(ether etherketone) (SPEEK) and previously synthesized MOF nanosheets (zinc(II) tetrakis(4-carboxy-phenyl)porphyrin) was spin-coated on the SPSF modified substrate (Fig. 16(a)). The formed membrane (MOF–SPEEK/SPSF) had a total thickness of 4.3 μm and displayed a good cation selectivity ascribed to the presence of sulfonated groups (Fig. 16(b)). Moreover, energy conversion experiments showed an enhancement of power output of the MOF–SPEEK/SPSF (6.96 W m−2) compared to those obtained with the SPSF (2.7 W m−2) and SPEEK/SPSF (5.95 W m−2) membranes when a 50-fold salinity gradient was applied (Fig. 16(c)). These results were attributed to both the asymmetrical structure and the diminution of ion transport resistance promoted by the high porosity of MOF. Furthermore, this value could be maximized to 7.9 W m−2 and 24 W m−2 by setting the pH = 11 and applying a 500-fold salinity gradient respectively (Fig. 16(d)). Finally, the authors introduced a novel method to apply a temperature gradient by irradiating a Si wafer with light.
 | ||
| Fig. 16 (a) Schematic illustration and (b) scanning electron microscopy image of the inorganic–organic composite membrane metal–organic framework–sulfonated poly(ether etherketone)–polysulfone (MOF–SPEEK/SPSF). The zoom-in image demonstrates the asymmetric structure. (c) Power density in terms of load resistance for the SPEEK/SPFS (M-1) and MOF–SPEEK/SPSF (M-2) membranes applying a 50-fold gradient. The integration of MOF in the heterogeneous membrane led to an increment in the output power. (d) Power density in terms of load resistance for the MOF–SPEEK/SPSF membrane applying a 500-fold gradient. Reproduced with permission.249 Copyright 2020 Elsevier Ltd. All rights reserved. | ||
The functionalization of nanochannels with different molecular systems has been one of the most applied approaches to obtain a high performance in multi-channel membranes.169,218,219,250–255 Liu et al. developed a highly selective nanoporous membrane based on the integration of the MOF UiO-66-NH2 onto the surface of a highly ordered AAO membrane (UiO-66-NH2–AAO).224 The composite membrane was created by in situ growth of the MOF UiO-66-NH2 onto a pre-synthesized AAO membrane modified with 3-triethoxysilylpropylamine (APTES). The previous modification of the AAO membrane with the APTES is a crucial step since it acts as a crosslinker enabling the successful integration of the MOF. Despite the asymmetric structure, the UiO-66-NH2–AAO membrane displayed a low rectifying behavior which was ascribed to the trade-off between asymmetric wettability and asymmetric pore-structure. The study of ion transport at different electrolyte concentrations showed a charge-governed transport below 1 M KCl due to the positively charged MOF and AAO membrane under neutral pH conditions. The ion-selective behavior was exploited in SGE experiments. The exposure of the composite membrane to asymmetric electrolyte concentrations (1000-fold KCl) evidenced the generation of I0 = 1.81 μA and Em = 72.7 mV when the MOF side was exposed to the concentrated solution (forward direction). The exposure of the MOF side to the diluted solution (the reverse direction) showed a clear diminution in the power capability. In this way, the analysis of power capabilities by P–R curves exhibited a respective value of 4.93 W m−2 and 7.12 W m−2 at 50-fold and 500-fold of KCl forward asymmetric concentration. Usually, it is assumed that the diffusion coefficients are the most relevant factor in the selection of the electrolyte. However, when nanoporous membranes based on MOFs are used, the hydrated ion radius acquires a central role due to the comparable magnitude of this parameter and the size of MOF cavities, as commented above. In this case, the performance as SGE of the composite membrane for a 100-fold gradient displayed power densities around 28.6 W m−2, 11.0 W m−2, and 0.0216 W m−2 for KBr, KCl, and KNO3 respectively. Considering that the relationship between hydrated anion radii is Br− (6.62 Å) < Cl− (6.64 Å) < NO3− (6.70 Å) and the pore size of UiO-66 is around 6–7 Å, this trend was attributed to partial size exclusions in the MOF porosity. Finally, the composite membrane presented good stability showing a loss in the power capability of only 12% after seven days.
Xin et al. introduced a heterogeneous nanofluidic device created by the deposition of the abundant biomaterial silk nanofibers (SNF) onto a porous AAO substrate (Fig. 17(a)).256 The hybrid membrane displayed interesting properties such as mechanical robustness, aqueous stability, long-term stability, and surface-charge-governed transport at high KCl concentration. The energy conversion properties were ascribed to the synergic mechanism of ion storage of the AAO substrate and the ionic selectivity of the SNF layer (Fig. 17(b)). Considering this mechanism, these authors ensured that the relationship between the size of SNF and AAO pores played a central role. On the one hand, an excessive decrease in the pore size of the AAO membrane (<70 nm) limited the effective contact between the SNF film and the AAO pores yielding a decrease in the power. On the other hand, an excessive increment in the pore size of the AAO membrane (>110 nm) reduced the ion storage capability of the AAO membrane diminishing the output power (Fig. 17(c)). Thus, by optimizing the pore size of the AAO membrane and the length of SNF film, this device was able to act as a nanopower generator with an artificial sea–river water system obtaining a maximum Pmax density of 2.86 W m−2 under alkaline conditions (Fig. 17(d)). This value was enhanced by incrementing the concentration gradient. Moreover, the system achieved SGE conversion efficiently in a broad range of pH (Fig. 17(e)).
 | ||
| Fig. 17 (a) Scheme of the hybrid membrane created by the integration of the silk nanofibers (SNFs) onto the anodic aluminum oxide (AAO) membrane. Scanning electron microscopy image (scale bar 0.2 μm) of the SNF surface containing pores with an average diameter of around ∼20 nm (inset). The Tindall effect promoted by the SNF solution is also shown. (b) Schematic representation of the AAO/SNF membrane. The AAO membrane acted as an ion storage layer, whereas the SNF film acted as an ion-selective layer. (c) Output power density in terms of the AAO pore size (the subindex refers to the pore size). Pore size between 80 and 100 nm led to an optimal response. (d) Extracted power density vs. the external resistance. (e) Power density as a function of the pH for two different SNF film thicknesses. The power displayed a maximum at basic pH. However, the hybrid system achieved a good performance in a broad range of pH. Reproduced with permission.256 Copyright 2020, The Author(s). Published by Springer Nature. | ||
Polymer membranes with a large pore density have been extensively used for the development of SGE devices.180,183,186,205,257,258 Similar to those results obtained in AAO, the main methodology is focused on the creation of heterogeneous membranes via the deposition of a highly charged layer on the membrane interface. For instance, Xu et al. presented the development of an asymmetric membrane by the integration of negatively charged 2,2,6,6-tetramethylpiperidine-1-oxyl radical oxidized cellulose nanofibers (TOCNs) (9 μm-thick) onto a porous track-etched PET substrate (12 μm-thick; pore density ∼108 pores per cm−2).182 The hybrid system displayed unique rectification properties and cation selectivity ascribed to the asymmetrical structure and the high negative charge density of the TOCN layer. Furthermore, supported by PNP simulations, the authors ensured that the heterogeneous membrane configuration allowed weakening of the ICP on the TOCN side. Exploiting these features, the NRED membrane showed a PDmax of ∼0.96 W m−2 with efficiencies around 25.2% mimicking the concentration gradient of seawater and river water. These values could be enhanced by alkalinizing the pH due to the deprotonation of carboxyl and hydroxyl groups of TOCNs and PET.
8 Upcoming challenges
Currently, there is vast knowledge about the main parameters affecting the energy performance in nanofluidic devices. Also, along Section 7, several articles based on up-scaled membranes either 2D or 3D materials achieving maximum power densities (PDmax) around or even exceeding the commercial benchmark (4–6 W m−2) have been reported (Fig. 18). Undoubtedly, great advances in the use of nanoporous membranes as NRED devices at the laboratory scale have been achieved in the last few years. However, in order to convert these novel innovations into technological platforms, several issues must be tackled. In principle, there are, at least, three important issues that need to be addressed in the immediate future: (a) scaling-up the systems to realistic working areas and to reduce the ICP impact, (b) creation of full NRED cells, and (c) improvement of the mechanical and antifouling properties of nanoporous membranes.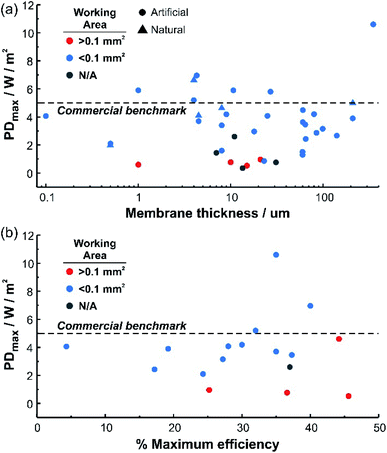 | ||
| Fig. 18 Maximum power density (PDmax) as a function of the membrane thickness (a) and the maximum efficiency (b) for most of the different studies addressed in Section 7. Data are also summarized in Table 1. | ||
8.1 Setting realistic scales for working areas
In Fig. 18, different reported PDmax values in terms of the membrane thickness are shown. Also, the color of the point indicates the working area employed. Results exposed in this figure denote the promising performances obtained in the last few years by employing nanoporous membranes. Furthermore, in several cases, the performances were compared (under the same conditions) with commercial membranes and these have shown overcoming energy capabilities.219 However, the working area employed in each case is still far away from realistic values that enable the real application of these platforms. Specifically, most of the studies exhibiting output powers around the commercial benchmark were obtained with working areas below 0.1 mm2. Considering that the degree of mixing with small areas is minimal, the driving force is maintained, and therefore, PDmax is maximized. However, under this condition, the amount of energy extracted is very low and therefore, constitutes a limitation.In the last few years, several authors have expressed the relevance of increasing the working areas in order to mimic the real operation conditions.124,208,238 The increment of the working area allows enhancement of the energy produced by a certain volume of solution (an increase of extractable energy efficiency) since this fact leads to transport of more moles of ions and, concomitantly, mixing of the solution. However, this increment dramatically affects the output power since more mixing reduces the gradient concentration and concomitantly, the driving force of SGE.108,238 Thus, to obtain an adequate balance between energy efficiency and PDmax, it is imperative to increase the working areas beyond the millimeter scale.
The trade-off between extractable energy and PDmax by increasing the working area can be related to the previously explained commitment relationship between the output power and pore-density due to the ICP effect (Section 6).107 While it is possible to despise this phenomenon in single-pore systems, ICP acquires a central role in nanoporous membranes. One way to analyze the ICP is considering that this leads to changes in the concentrations (or activities) at the membrane surface and, concomitantly, generates a diminution in the effective concentration gradient.108 As depicted in eqn (27), this diminution in the gradient magnitude and, therefore in the driving force of NRED, has a direct consequence on Pmax,
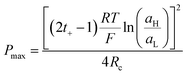 | (44) |
Analyzing from another perspective, it is possible to consider that the ICP generates an increase in the entering resistance (i.e. the resistance in the reservoir and at the membrane/reservoir interface) as a result of which the extracted power vanishes.107 Thus, beyond the conceptual richness of eqn (27), this equation is only applicable for ideal cases since if an equivalent electrical circuit is created, the presence of ICP (or diffusion boundary layers) introduces a new external resistance (in some articles referred to as boundary layer resistance, rBL). From a theoretical perspective, this resistance is not accounted for by eqn (27). However, it is so relevant that the increase of the membrane conductance (1/Rc) above 105 S m−2 could not increase the obtained power due to the dominant role of rBL.108
It is worth mentioning that, usually, the relationship between pore density and power has been mostly studied via numerical methods or in systems with very accurate control of porosity. Undoubtedly, these studies provided invaluable information about the fundamental basis of the scaling-up problem and constitute the foundations to address the creation of efficient membranes with high-pore density. However, it is necessary to be aware that, in practice, some additional issues not contemplated in fundamental studies could arise about this point. Some examples could involve the appearance of micrometer-sized defects and partial loss of mechanical properties due to the high porosity. In both cases, these facts could be another source of power capability loss. In this context, the scaling-up of nanoporous membranes remains a major challenge. In the last few years, several authors have found that the ICP can be diminished by optimizing several nanofluidic parameters such as channel size (see Section 6.4), channel length (see Section 6.3), the asymmetric integration of different building blocks (heterogeneous membranes) (see Section 6.5), or even the application of different temperature gradients (see Section 6.8).193,211,229
8.2 Full NRED cells
If the efficiency of extractable energy is considered, the use of a single nanoporous membrane (cation- or anion-selective) to construct the cell results in an inefficient NRED device (and even more if the currently employed working areas are considered).107,108 This configuration only enables the diffusion of one kind of ion and consequently, it only allows harvesting (in an ideal process) half of the Gibbs free energy available. In contrast, the stacking of cation-selective and anion-selective nanoporous membranes separated by concentrated and diluted solutions makes it possible to appreciably increase the open-circuit voltage. This full cell configuration employing nanofluidic devices has already shown some promising results.53,123 It is worth mentioning that while under ideal conditions the potential should scale linearly (eqn (42)), in practice, this increment rate is not achievable due to different sources of energy losses (e.g. ohmic resistance). In these cases, the optimization of several cell parameters, such as the reservoir thickness, is of paramount importance.108For its part, the creation of full NRED cells involves the generation of both anion-selective and cation-selective membranes and this fact is a challenge that needs to be further addressed.57 Considering the up-scaled devices cited in Table 1, only 25% of the reported systems correspond to anion-selective nanoporous membranes, which seem to be a major challenge.224
| Membrane type | Description | Thickness/μm | Gradient concentration | PDmax/W m−2 | %η | Working area/mm2 | Ref. |
|---|---|---|---|---|---|---|---|
| a N/A: not available. b For comparative purposes, mainly results at 50-fold gradients and under neutral pH conditions in up-scaled membranes were selected. In all cases, 50-fold gradient concentration corresponds to a gradient mimicking the sea/river water system, i.e. CH = 0.5 M and CL = 0.01 M. | |||||||
| 2D and ultrathin membranes | Graphene oxide membranes (membrane pair) | 10 | 50-fold (artificial, NaCl) | 0.77 | 36.6 | 0.8 | 123 |
| Graphene oxide membrane vertically oriented | 350 | 50-fold (artificial, NaCl) | 10.6 | 35 | ∼0.009 | 233 | |
| Graphene/CNF membrane | 9 | 50-fold (artificial, NaCl) | 4.19 | 30 | 0.03 | 228 | |
| Graphene/PPSU–Py copolymer | 31 | 50-fold (artificial, NaCl) | 0.76 | N/A | N/A | 237 | |
| Black phosphorus membrane | 8 | 50-fold (artificial, NaCl) | 1.6 | N/A | 0.03 | 170 | |
| Black phosphorus/graphene oxide composite membrane | 8 | 50-fold (artificial, NaCl) | 3.4 | N/A | 0.03 | 170 | |
| Black phosphorus/graphene oxide composite membrane | 8 | 150-fold (natural) | 4.7 | N/A | 0.03 | 170 | |
| MoS2 nanosheets/CNF composite membrane | 4 | 50-fold (artificial, NaCl) | 5.2 | 32 | 0.03 | 172 | |
| MoS2 nanosheets/CNF composite membrane | 4 | ∼50-fold (natural sea water) | 6.7 | N/A | 0.03 | 172 | |
| Ti3C2Tx membrane | 2.7 | 1000-fold (artificial, KCl) | 20.85 | 40.6 | 0.0163 | 175 | |
| Ti3C2Tx membrane | 15 | 50-fold (artificial, NaCl) | 0.53 | 45.6 | 0.78 | 241 | |
| Ti3C2Tx membranes (membrane pair) | N/A | 50-fold (artificial, NaCl) | 4.6 | 44.2 | 0.2 | 53 | |
| Ti3C2Tx membrane | N/A | 50-fold (artificial, NaCl) | 0.00168 (with light) | N/A | N/A | 203 | |
| Ti3C2Tx/ANF composite membrane | 4.5 | 50-fold (artificial, NaCl) | ∼3.7 | 35 | 0.03 | 208 | |
| Ti3C2Tx/ANF composite membrane | 4.5 | 150-fold (natural) | 4.1 | N/A | 0.03 | 208 | |
| ANF/boron nitride nanosheets | 1 | 50-fold (artificial, NaCl) | 5.9 | N/A | 0.03 | 124 | |
| ANF/boron nitride nanosheets | 1 | 50-fold (artificial, NaCl) | 0.6 | N/A | 3.14 | 124 | |
| Carbon nitride membrane | 0.25 | 1000-fold (artificial, KCl) | 0.21 | N/A | N/A | 166 | |
| Silk fibroin membrane | 0.1 | 50-fold (artificial, NaCl) | 4.06 | 4.3 | 0.03 | 289 | |
| Reconstructed nanokaolinite membranes | 25 | 100-fold (artificial, KCl) | 0.18 | 44.2 | 0.2 | 171 | |
| Block copolymer membrane | 0.5 | 50-fold (artificial, NaCl) | 2.1 | 24.3 | 0.03 | 209 | |
| Block copolymer membrane | 0.5 | Natural sea and river water | 2.04 | N/A | 0.03 | 209 | |
| Core–rim polycyclic aromatic hydrocarbon membrane | 2 × 10−3 | Artificial sea and river water | 67 | 8 | 3 × 10−6 | 113 | |
| 3D and multipore membranes | PAEK/PES composite membrane | 11 | 50-fold (artificial, NaCl) | 2.6 | 37 | N/A | 135 |
| SPEEK membrane | ∼27 | 50-fold (artificial, NaCl) | 5.8 | N/A | 0.03 | 65 | |
| Free-standing COF membrane | 10.7 | 50-fold (artificial, NaCl) | 5.9 | N/A | 0.03 | 248 | |
| MOF–SPEEK/SPSF composite membrane | 4.3 | 50-fold (artificial, NaCl) | 6.96 | 40 | 0.03 | 249 | |
| AAO/MOF (UiO-66-NH2) | ∼18 | 50-fold (artificial, NaCl) | 2.96 | N/A | 0.03 | 224 | |
| AAO/MOF (UiO-66-NH2) | ∼18 | 50-fold (artificial, KCl) | 4.93 | N/A | 0.03 | 224 | |
| AAO/MOF (UiO-66-NH2) | ∼18 | 100-fold (artificial, KBr) | 26.8 | 43.7 | 0.03 | 224 | |
| AAO/MOF-199–PSS | 85 | 50-fold (artificial, NaCl) | 2.87 | 0.03 | 218 | ||
| PSS/ANF | 210 | 50-fold (artificial, NaCl) | 3.9 | 19.2 | 0.03 | 64 | |
| PSS/ANF | 210 | 130-fold (natural) | 5.06 | N/A | 0.03 | 64 | |
| Polymer polyphenylsulphone with pyridine (PPSU–Pyx) | 7 | 50-fold (artificial, NaCl) | 1.44 | N/A | N/A | 244 | |
| AAO/mesoporous carbon | 64.2 | 50-fold (artificial, NaCl) | 3.46 | 37.3 | 0.03 | 219 | |
| AAO/silk nanofibers | 65 | 50-fold (artificial, NaCl) | 2.43 | 17.2 | 0.03 | 256 | |
| AAO/SPEEK | 80 | 50-fold (artificial, NaCl) | 4.2 | N/A | 0.03 | 181 | |
| PET/TOCNs | 21 | 50-fold (artificial, NaCl) | 0.96 | 25.2 | ∼9 | 182 | |
| PET/BCP (polystyrene-b-poly(4-vinylpyridine)) | 13.5 | 50-fold (artificial, NaCl) | 0.35 | N/A | N/A | 258 | |
| PET/Cyt C | 23 | 50-fold (artificial, NaCl) | 0.86 | N/A | 0.03 | 290 | |
| PC/Hydrogel (acrylic acid-co-acrylamide-co-methyl methacrylate) | 25 | 50-fold (artificial, NaCl) | 4.08 | ∼28 | 0.03 | 183 | |
| AAO/nanoporous polymeric membrane | ∼60 | 50-fold (artificial, KCl) | 1.3 | N/A | 0.03 | 252 | |
| AAO/nanoporous polymeric membrane | ∼60 | Natural sea and river water | 1.51 | N/A | 0.03 | 252 | |
| AAO/ionomer (copolymer of tetrafluoroethylene and perfluoro (4-methyl-3,6-dioxa-7-octene-1-sulfonic acid)) membrane | ∼99.2 | 50-fold (artificial, KCl) | 3.15 | 27.2 | 0.03 | 253 | |
| AAO/mesoporous silica | ∼60 | 50-fold (artificial, NaCl) | 4.5 | N/A | 0.03 | 250 | |
| AAO/polyamide and graphene oxide | ∼61.5 | 50-fold (artificial, NaCl) | 3.73 | N/A | 0.03 | 169 | |
| AAO/carbonaceous ordered mesoporous nanowires | ∼135 | 50-fold (artificial, NaCl) | 2.78 | N/A | 0.03 | 255 | |
| Ionized wood (pair) | 1000 | 60-fold (artificial, NaCl) | 0.005 | 46.1 | 100 | 259 | |
8.3 Improving the mechanical and antifouling properties of membranes
The membrane can be considered the heart of RED and NRED devices and, for this reason, it is highly desirable that certain features related to their mechanical and antifouling properties are accomplished. In Section 5, Nanofabrication methods, the main methods used for the development of NRED devices were introduced. Aiming to convert these novel platforms into applicable devices, the nanofabrication methods and the materials must enable us to not only obtain membranes with mechanical properties that ensure long durability but also easy and low-cost scalability.57 Considering the eventual challenge of large-scale production, the study of different straightforward and robust chemical routes for the reproducible development of nanoporous membranes is needed. In this way, some studies have shown interesting procedures for the development of efficient membranes by combining relatively simple protocols and bioabundant materials.256,259 However, until now, these issues have not been exhaustively studied.Moreover, in contrast to laboratory experiments, water sources employed in up-scaled RED devices are expected to contain different non-desirable inorganic, organic and microbial constituents.107,260 This acquires more relevance when the system operates with natural sea and river water since these materials could deposit onto the membrane promoting a dramatic decrease in the energy capabilities especially in anion-selective membranes.261,262 Affordable ways to prevent fouling could involve the integration of different building blocks onto the NRED membrane surface with antifouling properties.52,263,264 In this regard, the functionalization of membranes with 2D materials with antifouling properties has been highlighted as an interesting alternative.57 Besides, in all the cases, the pretreatment of water and defouling generate non-negligible energy consumption. In order to be economically viable, these costs must also be afforded by the NRED system. Considering the early stage of development of NRED, this issue also remains scarcely studied.
8.4 Expanding the SGE possibilities
As has been addressed throughout the review, the current state of RED is not still completely viable in economic terms. On the other hand, while the use of nanoporous membranes has shown promising results at the laboratory scale, its future at the large scale is also uncertain. In this context, to expand the possibilities of SGE-based methods, researchers have proposed different alternatives such as desalination and energy conversion. In general, these alternatives were applied in RED systems rather than NRED. In this line, in order to analyze the economic potential of NRED, the study of these different alternatives will be imperative. In the following, these alternatives will be briefly explained (for further details ref. 18 is recommended).9 Conclusions and perspectives
In summary, lab-scale experiments to generate sustainable and low-environmental impact from saline gradients employing nanofluidic devices have shown promising results. The reason is associated with the increment in the balance between resistance and selectivity displayed in nanofluidic membranes. Also, there is vast knowledge about the impact of different experimental variables such as electrolyte gradient, structural parameters, pH, and temperature, on the SGE conversion performance of nanoporous membranes. Undoubtedly, interdisciplinary efforts from different fields such as materials science, engineering, nanotechnology, and electrochemistry, will be key in the further growth of this emerging field. In particular, the integration of different building blocks for the creation of hybrid (or heterogeneous) nanoporous membranes based on either ultrathin, 2D, 3D, or multi-channel materials has shown to be an interesting alternative to find a good balance between ion selectivity and low ion resistance. By exploiting this strategy, a considerable amount of new nanoporous membranes displayed a response exceeding (or around) the commercial benchmark at laboratory scale (Fig. 18 and Table 1).While the results obtained in the last few years are promising, there are some conditions and concepts that remain scarcely studied and need to be addressed in the immediate future. So far, most of the reported results were obtained using small working areas, which are not adequate for real applications as the great results in terms of power density and efficiency come together with low net energy values. As it was exposed, the increment in the working area results in a detriment in the power density, and therefore, it is an issue that must be tackled to convert these lab-scale innovations into promising technological platforms with real applications. Also, the transference of results obtained in single-pore systems to upscaled nanoporous membranes remains a challenge, the reason behind this behavior is related to the ICP effect and consequently, the drastic diminution in the driving force of salinity gradient power, the effective concentration gradient. These issues are perhaps the main problems to be faced in the immediate future.
On the other hand, most of the studies introduced in NRED are based on half-cells, i.e. the cell is constituted by a single nanoporous membrane (anion or cation-selective) separating the reservoirs with the concentrated and diluted solutions. These configurations are ideal to study the performance of new membranes but, in order to enhance the extracted energy, it is also important to consider the design of full cells. This issue opens the doors to different problems still scarcely studied. For instance, the construction of full cells is linked to the availability of both cation and anion-selective membranes. While the design of efficient up-scaled nanoporous membranes has rapidly grown over the last few years, it is important to look for further chemical and nanofabrication routes conferring optimum mechanical properties and promising scalability. Moreover, except for some examples of anion-selective membranes with appreciable energy-conversion performance, the design of this kind of membrane, in particular, is still a major challenge. On the other hand, the importance of scaling the systems to full cells brings with it the need to optimize several parameters related to the cell architecture, fluid management, and electrodes to diminish the energy loss.285
Usually, NRED is designed to be applied to sea and river water due to their wide availability. However, the aperture to different effluents could not only increase the technological potential of this emerging field but also enables the exploitation of different water and organic wastes. In this regard, the understanding of ion transport and specifically, the energy conversion properties of these nanoporous membranes exposed to organic solvents remains limited. Furthermore, beyond the specific source, the use of different waste or natural effluents involves the presence of different non-desirable compounds. This fact denotes the importance of implementing different antifouling strategies to supply the NRED systems. Again, this highlights the importance of further developing different chemical and physical routes for the creation of nanoporous membranes with not only tailorable ion transport but also fulfilling other requirements related to the cost, scalability, and long-term stability.
It is important to highlight the wide range of opportunities to couple NRED systems with different devices and technologies. Considering that NRED is in the early stage of development, this issue has not been deeply addressed. Nevertheless, several examples are employing RED systems combined with other technologies to expand the possibilities of this field.18 In this regard, several authors have proposed different ways of storing the energy provided by RED.265–267 Also, by taking advantage of low-grade waste heat, RED systems can be used in a closed-loop.232 The RED devices can be coupled with different desalination technologies enabling both a decrease in energy consumption and environmental impact.277,278,286 Finally, several authors have proposed the use of RED for water remediation by the direct or indirect reactions in the electrode chambers.287,288 These applications need to be addressed in the years to come.
Even though much work still needs to be done to turn the lab-scale nanoporous membranes into platforms with real applications, the results obtained in this emerging field are promising.
Author contributions
All the authors contributed to the bibliographic research, discussion, writing and revision of the article.Conflicts of interest
There are no conflicts to declare.Acknowledgements
G. L. acknowledges a doctoral scholarship from CONICET and a short-term grant from DAAD. G. L. would also like to acknowledge the support of the GET_INvolved program of GSI. W. A. M. and O. A. are CONICET fellows and acknowledge financial support from Universidad Nacional de La Plata (PID-X867) and ANPCyT (PICT-2017-1523 and PICT-2016-1680). C. T. and M. E. T. M. acknowledge support by the LOEWE project iNAPO funded by the Hessen State Ministry of Higher Education, Research and Arts.References
- S. Chu, Y. Cui and N. Liu, Nat. Mater., 2017, 16, 16–22 CrossRef.
- S. Chu and A. Majumdar, Nature, 2012, 488, 294–303 CrossRef CAS.
- P. A. Østergaard, N. Duic, Y. Noorollahi, H. Mikulcic and S. Kalogirou, Renewable Energy, 2020, 146, 2430–2437 CrossRef.
- M. S. Nazir, A. J. Mahdi, M. Bilal, H. M. Sohail, N. Ali and H. M. N. Iqbal, Sci. Total Environ., 2019, 683, 436–444 CrossRef CAS.
- A. Hussain, S. M. Arif and M. Aslam, Renewable Sustainable Energy Rev., 2017, 71, 12–28 CrossRef.
- E. Kabir, P. Kumar, S. Kumar, A. A. Adelodun and K.-H. Kim, Renewable Sustainable Energy Rev., 2018, 82, 894–900 CrossRef.
- B. E. Logan and M. Elimelech, Nature, 2012, 488, 313–319 CrossRef CAS.
- G. Z. Ramon, B. J. Feinberg and E. M. V. V. Hoek, Energy Environ. Sci., 2011, 4, 4423 RSC.
- S. E. Skilhagen, Desalin. Water Treat., 2010, 15, 271–278 CrossRef.
- N. Y. Yip and M. Elimelech, Environ. Sci. Technol., 2012, 46, 5230–5239 CrossRef CAS.
- A. Siria, M.-L. Bocquet and L. Bocquet, Nat. Rev. Chem., 2017, 1, 0091 CrossRef CAS.
- R. E. Pattle, Nature, 1954, 174, 660 CrossRef CAS.
- R. S. Norman, Science, 1974, 186, 350–352 CrossRef CAS PubMed.
- S. Loeb, Method and apparatus for generating power utilizing pressure-retarded-osmosis, US Pat., US3906250A, Sept. 16,1975 Search PubMed.
- S. Loeb, Method and apparatus for generating power utilizing reverse electrodialysis, US Pat., US4171409A, Oct. 16, 1979 Search PubMed.
- R. E. Lacey, Ocean Eng., 1980, 7, 1–47 CrossRef CAS.
- M. Tedesco, E. Brauns, A. Cipollina, G. Micale, P. Modica, G. Russo and J. Helsen, J. Membr. Sci., 2015, 492, 9–20 CrossRef CAS.
- H. Tian, Y. Wang, Y. Pei and J. C. Crittenden, Appl. Energy, 2020, 262, 114482 CrossRef CAS.
- J. W. Post, J. Veerman, H. V. M. M. Hamelers, G. J. W. W. Euverink, S. J. Metz, K. Nymeijer and C. J. N. N. Buisman, J. Membr. Sci., 2007, 288, 218–230 CrossRef.
- D. Brogioli, R. Zhao and P. M. Biesheuvel, Energy Environ. Sci., 2011, 4, 772 RSC.
- D. Brogioli, Phys. Rev. Lett., 2009, 103, 058501 CrossRef PubMed.
- R. A. Tufa, E. Curcio, E. Fontananova and G. Di Profio, in Comprehensive Membrane Science and Engineering, Elsevier, 2017, pp. 206–248 Search PubMed.
- M. Tedesco, A. Cipollina, A. Tamburini and G. Micale, J. Membr. Sci., 2017, 522, 226–236 CrossRef CAS.
- M. Tedesco, C. Scalici, D. Vaccari, A. Cipollina, A. Tamburini and G. Micale, J. Membr. Sci., 2016, 500, 33–45 CrossRef CAS.
- https://www.redstack.nl/ .
- R. A. Tufa, S. Pawlowski, J. Veerman, K. Bouzek, E. Fontananova, G. di Profio, S. Velizarov, J. Goulão Crespo, K. Nijmeijer and E. Curcio, Appl. Energy, 2018, 225, 290–331 CrossRef CAS.
- A. Daniilidis, R. Herber and D. A. Vermaas, Appl. Energy, 2014, 119, 257–265 CrossRef.
- M. Tagliazucchi and I. Szleifer, Chemically Modified Nanopores and Nanochannels, Elsevier Inc., 1st edn, 2016 Search PubMed.
- G. Pérez-Mitta, C. Trautmann, M. E. Toimil-Molares and O. Azzaroni, in Chemically Modified Nanopores and Nanochannels, ed. M. Tagliazucchi and I. Szleifer, Elsevier, 2017, pp. 61–83 Search PubMed.
- M. Tagliazucchi and I. Szleifer, Mater. Today, 2015, 18, 131–142 CrossRef CAS.
- Z. Zhang, L. Wen and L. Jiang, Chem. Soc. Rev., 2018, 47, 322–356 RSC.
- X. Hou, W. Guo and L. Jiang, Chem. Soc. Rev., 2011, 40, 2385–2401 RSC.
- C. Dekker, Nat. Nanotechnol., 2007, 2, 209–215 CrossRef CAS.
- G. Laucirica, Y. Toum Terrones, V. M. Cayón, M. L. Cortez, M. E. Toimil-Molares, C. Trautmann, W. A. Marmisollé and O. Azzaroni, Nanoscale, 2020, 12, 18390–18399 RSC.
- G. Pérez-Mitta, A. S. Peinetti, M. L. Cortez, M. E. Toimil-Molares, C. Trautmann and O. Azzaroni, Nano Lett., 2018, 18, 3303–3310 CrossRef.
- G. Laucirica, G. Pérez-Mitta, M. E. M. E. Toimil-Molares, C. Trautmann, W. A. W. A. Marmisollé and O. Azzaroni, J. Phys. Chem. C, 2019, 123, 28997–29007 CrossRef.
- P. Wang, M. Wang, F. Liu, S. Ding, X. Wang, G. Du, J. Liu, P. Apel, P. Kluth, C. Trautmann and Y. Wang, Nat. Commun., 2018, 9, 569 CrossRef PubMed.
- G. Pérez-Mitta, W. A. Marmisolle, L. Burr, M. E. Toimil-Molares, C. Trautmann and O. Azzaroni, Small, 2018, 14, 1703144 CrossRef.
- G. Xie, L. Wen and L. Jiang, Nano Res., 2016, 9, 59–71 CrossRef.
- R. Li, X. Fan, Z. Liu and J. Zhai, Adv. Mater., 2017, 29, 1702983 CrossRef.
- K. Xiao, L. Jiang and M. Antonietti, Joule, 2019, 3, 2364–2380 CrossRef CAS.
- L. Wen, X. Hou, Y. Tian, J. Zhai and L. Jiang, Adv. Funct. Mater., 2010, 20, 2636–2642 CrossRef CAS.
- Y. Feng, W. Zhu, W. Guo and L. Jiang, Adv. Mater., 2017, 29, 1702773 CrossRef PubMed.
- R. Qu, X. Zeng, L. Lin, G. Zhang, F. Liu, C. Wang, S. Ma, C. Liu, H. Miao and L. Cao, ACS Nano, 2020, 14, 16654–16662 CrossRef CAS PubMed.
- J. Feng, M. Graf, K. Liu, D. Ovchinnikov, D. Dumcenco, M. Heiranian, V. Nandigana, N. R. Aluru, A. Kis and A. Radenovic, Nature, 2016, 536, 197–200 CrossRef CAS.
- A. Siria, P. Poncharal, A. Biance, R. Fulcrand, X. Blasé, S. T. Purcell and L. Bocquet, Nature, 2013, 494, 455–458 CrossRef CAS PubMed.
- Y. Xie, X. Wang, J. Xue, K. Jin, L. Chen and Y. Wang, Appl. Phys. Lett., 2008, 93, 163116 CrossRef.
- F. Qian, W. Zhang, D. Huang, W. Li, Q. Wang and C. Zhao, Phys. Chem. Chem. Phys., 2020, 22, 2386–2398 RSC.
- F. H. J. Van Der Heyden, D. Stein and C. Dekker, Phys. Rev. Lett., 2005, 95, 9–12 CrossRef.
- J. Cervera, A. Alcaraz, B. Schiedt, R. Neumann and P. Ramírez, J. Phys. Chem. C, 2007, 111, 12265–12273 CrossRef CAS.
- W. Guo, L. Cao, J. Xia, F. Q. Nie, M. Wen, J. Xue, Y. Song, D. Zhu, Y. Wang and L. Jiang, Adv. Funct. Mater., 2010, 20, 1339–1344 CrossRef CAS.
- Z. Jia, B. Wang, S. Song and Y. Fan, Renewable Sustainable Energy Rev., 2014, 31, 91–100 CrossRef.
- L. Ding, D. Xiao, Z. Lu, J. Deng, Y. Wei, J. Caro and H. Wang, Angew. Chem., 2020, 132, 8798–8804 CrossRef.
- T. Thorsen and T. Holt, J. Membr. Sci., 2009, 335, 103–110 CrossRef CAS.
- K. Gerstandt, K.-V. Peinemann, S. E. Skilhagen, T. Thorsen and T. Holt, Desalination, 2008, 224, 64–70 CrossRef CAS.
- K. Xiao, L. Wen and L. Jiang, Small, 2016, 12, 2810–2831 CrossRef CAS.
- M. Macha, S. Marion, V. V. R. Nandigana and A. Radenovic, Nat. Rev. Mater., 2019, 4, 588–605 CrossRef CAS.
- Y. Zhu, K. Zhan and X. Hou, ACS Nano, 2018, 12, 908–911 CrossRef CAS.
- R. Spohr, Ion Tracks and Microtechnology, Vieweg+Teubner Verlag, Wiesbaden, 1st edn, 1990 Search PubMed.
- W. Kim and S. Nair, Chem. Eng. Sci., 2013, 104, 908–924 CrossRef CAS.
- Y. Kang, Y. Xia, H. Wang and X. Zhang, Adv. Funct. Mater., 2019, 29, 1902014 CrossRef.
- Y. Zhou and L. Jiang, Joule, 2020, 4, 2244–2248 CrossRef.
- G. Laucirica, A. G. Albesa, M. E. Toimil-Molares, C. Trautmann, W. A. Marmisollé and O. Azzaroni, Nano Energy, 2020, 71, 104612 CrossRef CAS.
- Z. Zhang, L. He, C. Zhu, Y. Qian, L. Wen and L. Jiang, Nat. Commun., 2020, 11, 875 CrossRef CAS PubMed.
- Y. Zhao, J. Wang, X.-Y. Kong, W. Xin, T. Zhou, Y. Qian, L. Yang, J. Pang, L. Jiang and L. Wen, Natl. Sci. Rev., 2020, 7, 1349–1359 CrossRef CAS.
- A. J. Bard and L. R. Faulkner, Electrochemical Methods. Fundamentals and Applications, Wiley, USA, 2nd edn, 2001 Search PubMed.
- J. N. Israelachvili, Intermolecular and Surface Forces, Elsevier, 3rd edn, 2011 Search PubMed.
- C. M. A. Brett and A. M. Oliveira Brett, Electrochemistry: Principles, Methods, and Applications, Oxford University Press, USA, 1993 Search PubMed.
- G. Pérez-Mitta, M. E. Toimil-Molares, C. Trautmann, W. A. Marmisollé and O. Azzaroni, Adv. Mater., 2019, 31, 1901483 CrossRef PubMed.
- P. C. Hiemenz and R. Rajagopalan, Principles of Colloid and Surface Chemistry, Marcel Dekker, 3rd edn, 1997 Search PubMed.
- H.-J. Butt, K. Graf and M. Kappl, Physics and Chemistry of Interfaces, 2003 Search PubMed.
- T. Ma, J. M. Janot and S. Balme, Small Methods, 2020, 4, 1–36 Search PubMed.
- I. Vlassiouk, S. Smirnov, Z. Siwyt and Z. Siwy, Nano Lett., 2008, 8, 1978–1985 CrossRef CAS.
- R. B. Schoch and P. Renaud, Appl. Phys. Lett., 2005, 86, 253111 CrossRef.
- A. R. Poggioli, A. Siria and L. Bocquet, J. Phys. Chem. B, 2019, 123, 1171–1185 CrossRef CAS.
- L. Bocquet and J.-L. Barrat, Soft Matter, 2007, 3, 685 RSC.
- S. Marbach and L. Bocquet, Chem. Soc. Rev., 2019, 48, 3102–3144 RSC.
- L. Joly, C. Ybert, E. Trizac and L. Bocquet, J. Chem. Phys., 2006, 125, 204716 CrossRef PubMed.
- L. Joly, C. Ybert, E. Trizac and L. Bocquet, Phys. Rev. Lett., 2004, 93, 257805 CrossRef PubMed.
- Q. Xie, M. A. Alibakhshi, S. Jiao, Z. Xu, M. Hempel, J. Kong, H. G. Park and C. Duan, Nat. Nanotechnol., 2018, 13, 238–245 CrossRef CAS PubMed.
- T. Mouterde and L. Bocquet, Eur. Phys. J. E: Soft Matter Biol. Phys., 2018, 41, 148 CrossRef.
- D. J. Rankin and D. M. Huang, Langmuir, 2016, 32, 3420–3432 CrossRef CAS.
- R. Long, Y. Zhao, Z. Kuang, Z. Liu and W. Liu, Desalination, 2020, 477, 114263 CrossRef CAS.
- L. Ma, K. Lin, Y. Qiu, J. Zhuang, X. An, Z. Yuan and C. Huang, J. Phys. Chem. C, 2021, 125, 14195–14203 CrossRef CAS.
- J. Kuleszo, C. Kroeze, J. Post and B. M. Fekete, J. Integr. Environ. Sci., 2010, 7, 89–96 CrossRef.
- O. A. Alvarez-Silva, A. F. Osorio and C. Winter, Renewable Sustainable Energy Rev., 2016, 60, 1387–1395 CrossRef.
- X. Gao and C. Kroeze, J. Integr. Environ. Sci., 2012, 9, 177–190 CrossRef.
- J. W. Post, C. H. Goeting, J. Valk, S. Goinga, J. Veerman, H. V. M. Hamelers and P. J. F. M. Hack, Desalin. Water Treat., 2010, 16, 182–193 CrossRef CAS.
- S. Pawlowski, J. Crespo and S. Velizarov, in Electrokinetics Across Disciplines and Continents, Springer International Publishing, Cham, 2016, pp. 57–80 Search PubMed.
- K. Nijmeijer and S. Metz, in Sustainability Science and Engineering, 2010, vol 2, pp. 95–139 Search PubMed.
- A. Cipollina and M. Giorgio, Sustainable Energy from Salinity Gradients, Elsevier/Woodhead Publishing, 2016 Search PubMed.
- J. W. Post, H. V. M. Hamelers and C. J. N. Buisman, Environ. Sci. Technol., 2008, 42, 5785–5790 CrossRef CAS PubMed.
- L. Zhang and X. Chen, Angew. Chem., Int. Ed., 2013, 52, 7640–7641 CrossRef CAS PubMed.
- A. Campione, L. Gurreri, M. Ciofalo, G. Micale, A. Tamburini and A. Cipollina, Desalination, 2018, 434, 121–160 CrossRef CAS.
- H. Strathmann, Ion-Exchange Membrane Separation Processes, Elsevier Science, 1st edn, 2004, vol. 9 Search PubMed.
- H. Strathmann, A. Grabowski and G. Eigenberger, Ind. Eng. Chem. Res., 2013, 52, 10364–10379 CrossRef CAS.
- N. Lakshminarayanaiah, Equations of Membrane Biophysics, Academic Press Inc., UK, 1984 Search PubMed.
- A. H. Galama, J. W. Post, H. V. M. Hamelers, V. V. Nikonenko and P. M. Biesheuvel, J. Membr. Sci. Res., 2016, 2, 128–140 Search PubMed.
- Y. Tanaka, Ion Exchange Membranes - Fundamentals and Applications, Elsevier, 2007, vol. 12 Search PubMed.
- P. Ramirez, J. Cervera, V. Gomez, M. Ali, S. Nasir, W. Ensinger and S. Mafe, J. Membr. Sci., 2019, 573, 579–587 CrossRef CAS.
- J. Kim, S. J. Kim and D. K. Kim, Energy, 2013, 51, 413–421 CrossRef CAS.
- D. K. Kim, C. Duan, Y. F. Chen and A. Majumdar, Microfluid. Nanofluid., 2010, 9, 1215–1224 CrossRef CAS.
- H. C. Yeh, C. C. Chang and R. J. Yang, RSC Adv., 2014, 4, 2705–2714 RSC.
- J. Veerman and D. A. Vermaas, in Sustainable Energy from Salinity Gradients, Elsevier, 2016, pp. 77–133 Search PubMed.
- J. P. Hsu, S. C. Lin, C. Y. Lin and S. Tseng, J. Power Sources, 2017, 366, 169–177 CrossRef CAS.
- J. Su, D. Ji, J. Tang, H. Li, Y. Feng, L. Cao, L. Jiang and W. Guo, Chin. J. Chem., 2018, 36, 417–420 CrossRef CAS.
- X. Tong, S. Liu, J. Crittenden and Y. Chen, ACS Nano, 2021, 15, 5838–5860 CrossRef CAS PubMed.
- Z. Wang, L. Wang and M. Elimelech, Engineering DOI:10.1016/j.eng.2021.02.016.
- J. C. Fair and J. F. Osterle, J. Chem. Phys., 1971, 54, 3307 CrossRef CAS.
- N. Y. Yip, D. A. Vermaas, K. Nijmeijer and M. Elimelech, Environ. Sci. Technol., 2014, 48, 4925–4936 CrossRef CAS PubMed.
- B. V. Derjaguin, S. S. Dukhin and M. M. Koptelova, J. Colloid Interface Sci., 1972, 38, 584–595 CrossRef.
- C. Lee, C. Cottin-Bizonne, A.-L. Biance, P. Joseph, L. Bocquet and C. Ybert, Phys. Rev. Lett., 2014, 112, 244501 CrossRef CAS PubMed.
- X. Liu, M. He, D. Calvani, H. Qi, K. B. S. S. Gupta, H. J. M. de Groot, G. J. A. Sevink, F. Buda, U. Kaiser and G. F. Schneider, Nat. Nanotechnol., 2020, 15, 307–312 CrossRef CAS PubMed.
- G. Laucirica, M. E. Toimil-Molares, C. Trautmann, W. A. Marmisollé and O. Azzaroni, ACS Appl. Mater. Interfaces, 2020, 12, 28148–28157 CrossRef CAS PubMed.
- R. S. Kingsbury, S. Flotron, S. Zhu, D. F. Call and O. Coronell, Environ. Sci. Technol., 2018, 52, 4929–4936 CrossRef CAS PubMed.
- H. Wang, L. Su, M. Yagmurcukardes, J. Chen, Y. Jiang, Z. Li, A. Quan, F. M. Peeters, C. Wang, A. K. Geim and S. Hu, Nano Lett., 2020, 20, 8634–8639 CrossRef CAS PubMed.
- W. Ouyang, W. Wang, H. Zhang, W. Wu and Z. Li, Nanotechnology, 2013, 24, 345401 CrossRef PubMed.
- D.-C. Zheng and L.-H. Yeh, Micromachines, 2020, 11, 949 CrossRef PubMed.
- M. Gao, P. Tsai, Y. Su, P. Peng and L. Yeh, Small, 2020, 16, 2006013 CrossRef CAS PubMed.
- E. Güler and K. Nijmeijer, J. Membr. Sci. Res., 2018, 4, 108–110 Search PubMed.
- J. Veerman, M. Saakes, S. J. Metz and G. J. Harmsen, Environ. Sci. Technol., 2010, 44, 9207–9212 CrossRef CAS PubMed.
- R. Long, B. Li, Z. Liu and W. Liu, Energy, 2018, 158, 427–436 CrossRef.
- J. Ji, Q. Kang, Y. Zhou, Y. Feng, X. Chen, J. Yuan, W. Guo, Y. Wei and L. Jiang, Adv. Funct. Mater., 2017, 27, 1603623 CrossRef.
- C. Chen, D. Liu, L. He, S. Qin, J. Wang, J. M. Razal, N. A. Kotov and W. Lei, Joule, 2020, 4, 247–261 CrossRef CAS.
- J. Wang, M. Zhang, J. Zhai and L. Jiang, Phys. Chem. Chem. Phys., 2014, 16, 23–32 RSC.
- S. Tseng, Y. M. Li, C. Y. Lin and J. P. Hsu, Nanoscale, 2016, 8, 2350–2357 RSC.
- S. Tseng, Y. Li, C. Lin and J. Hsu, Electrochim. Acta, 2016, 219, 790–797 CrossRef CAS.
- J.-P. Hsu, T.-C. Su, C.-Y. Lin and S. Tseng, Electrochim. Acta, 2019, 294, 84–92 CrossRef CAS.
- F. Xiao, D. Ji, H. Li, J. Tang, Y. Feng, L. Ding, L. Cao, N. Li, L. Jiang and W. Guo, Inorg. Chem. Front., 2018, 5, 1677–1682 RSC.
- F. Xiao, D. Ji, H. Li, J. Tang, Y. Feng, L. Ding, L. Cao, N. Li, L. Jiang and W. Guo, Mater. Chem. Front., 2018, 2, 935–941 RSC.
- Z. S. Siwy, Adv. Funct. Mater., 2006, 16, 735–746 CrossRef CAS.
- V. M. Cayón, G. Laucirica, Y. Toum Terrones, M. L. Cortez, G. Pérez-Mitta, J. Shen, C. Hess, M. E. Toimil-Molares, C. Trautmann, W. A. Marmisollé and O. Azzaroni, Nanoscale, 2021, 13, 11232–11241 RSC.
- G. Laucirica, W. A. Marmisollé, M. E. Toimil-Molares, C. Trautmann and O. Azzaroni, ACS Appl. Mater. Interfaces, 2019, 11, 30001–30009 CrossRef CAS PubMed.
- G. Pérez-Mitta, A. Albesa, F. M. Gilles, M. E. Toimil-Molares, C. Trautmann and O. Azzaroni, J. Phys. Chem. C, 2017, 121, 9070–9076 CrossRef.
- X. Zhu, J. Hao, B. Bao, Y. Zhou, H. Zhang, J. Pang, Z. Jiang and L. Jiang, Sci. Adv., 2018, 4, eaau1665 CrossRef CAS PubMed.
- C. Trautmann, in Ion Beams in Nanoscience and Technology, ed. R. Hellborg, H. J. Whitlow and Y. Zhang, Springer-Verlag Berlin Heidelberg, 2009, pp. 369–387 Search PubMed.
- Z. Siwy and A. Fuliński, Am. J. Physiol., 2004, 72, 567–574 CrossRef CAS.
- P. Y. Apel, Y. E. Korchev, Z. Siwy, R. Spohr and M. Yoshida, Nucl. Instrum. Methods Phys. Res., Sect. B, 2001, 184, 337–346 CrossRef CAS.
- Z. Siwy, P. Apel, D. Baur, D. D. Dobrev, Y. E. Korchev, R. Neumann, R. Spohr, C. Trautmann and K. O. Voss, Surf. Sci., 2003, 532–535, 1061–1066 CrossRef CAS.
- M. E. Toimil-Molares, Beilstein J. Nanotechnol., 2012, 3, 860–883 CrossRef PubMed.
- P. Y. Apel and D. Fink, in Transport Processes in Ion-Irradiated Polymers, ed. D. Fink, Springer-Verlag Berlin Heidelberg, 2004, pp. 147–202 Search PubMed.
- C. Trautmann, W. Brüchle, R. Spohr, J. Vetter and N. Angert, Nucl. Instrum. Methods Phys. Res., Sect. B, 1996, 111, 70–74 CrossRef CAS.
- G. Pérez-Mitta, W. A. Marmisollé, A. G. Albesa, M. E. Toimil-Molares, C. Trautmann and O. Azzaroni, Small, 2018, 14, 1702131 CrossRef PubMed.
- G. Pérez-Mitta, A. G. Albesa, W. Knoll, C. Trautmann, M. E. Toimil-Molares and O. Azzaroni, Nanoscale, 2015, 7, 15594–15598 RSC.
- L. C. T. Man, P. Apel, T. Cheung, L. Westerberg, K. N. Yu, C. Zet and R. Spohr, Nucl. Instrum. Methods Phys. Res., Sect. B, 2007, 265, 621–625 CrossRef CAS.
- P. Y. Apel, I. V. Blonskaya, S. N. Dmitriev, O. L. Orelovitch, A. Presz and B. A. Sartowska, Nanotechnology, 2007, 18, 305302 CrossRef.
- Z. Siwy and A. Fuliński, Phys. Rev. Lett., 2002, 89, 4–7 Search PubMed.
- G. Laucirica, V. M. Cayón, Y. Toum Terrones, M. L. Cortez, M. E. Toimil-Molares, C. Trautmann, W. A. Marmisollé and O. Azzaroni, Nanoscale, 2020, 12, 6002–6011 RSC.
- N. Li, D. T. Mitchell, K.-P. Lee and C. R. Martin, J. Electrochem. Soc., 2003, 150, A979 CrossRef CAS.
- H. Masuda and K. Fukuda, Science, 1995, 268, 1466–1468 CrossRef CAS PubMed.
- R. C. Furneaux, W. R. Rigby and A. P. Davidson, Nature, 1989, 337, 147–149 CrossRef CAS.
- J. H. Yuan, F. Y. He, D. C. Sun and X. H. Xia, Chem. Mater., 2004, 16, 1841–1844 CrossRef CAS.
- L. A. Baker, P. Jin and C. R. Martin, Crit. Rev. Solid State Mater. Sci., 2005, 30, 183–205 CrossRef CAS.
- A.-L. Biance, J. Gierak, É. Bourhis, A. Madouri, X. Lafosse, G. Patriarche, G. Oukhaled, C. Ulysse, J.-C. Galas, Y. Chen and L. Auvray, Microelectron. Eng., 2006, 83, 1474–1477 CrossRef CAS.
- J. Gierak, A. Madouri, A. L. Biance, E. Bourhis, G. Patriarche, C. Ulysse, D. Lucot, X. Lafosse, L. Auvray, L. Bruchhaus and R. Jede, Microelectron. Eng., 2007, 84, 779–783 CrossRef CAS.
- P. Chen, M.-Y. Wu, H. W. M. Salemink and P. F. A. Alkemade, Nanotechnology, 2009, 20, 015302 CrossRef CAS PubMed.
- J. Li, M. Gershow, D. Stein, E. Brandin and J. A. Golovchenko, Nat. Mater., 2003, 2, 611–615 CrossRef CAS PubMed.
- J. Li, D. Stein, C. McMullan, D. Branton, M. J. Aziz and J. A. Golovchenko, Nature, 2001, 412, 166–169 CrossRef CAS PubMed.
- J. Feng, K. Liu, M. Graf, M. Lihter, R. D. Bulushev, D. Dumcenco, D. T. L. Alexander, D. Krasnozhon, T. Vuletic, A. Kis and A. Radenovic, Nano Lett., 2015, 15, 3431–3438 CrossRef CAS PubMed.
- A. J. Storm, J. H. Chen, X. S. Ling, H. W. Zandbergen and C. Dekker, Nat. Mater., 2003, 2, 537–540 CrossRef CAS.
- S. Liu, Q. Zhao, J. Xu, K. Yan, H. Peng, F. Yang, L. You and D. Yu, Nanotechnology, 2012, 23, 085301 CrossRef PubMed.
- J. B. Heng, C. Ho, T. Kim, R. Timp, A. Aksimentiev, Y. V. Grinkova, S. Sligar, K. Schulten and G. Timp, Biophys. J., 2004, 87, 2905–2911 CrossRef CAS.
- A. J. Storm, J. H. Chen, X. S. Ling, H. W. Zandbergen and C. Dekker, J. Appl. Phys., 2005, 98, 014307 CrossRef.
- M. J. Kim, M. Wanunu, D. C. Bell and A. Meller, Adv. Mater., 2006, 18, 3149–3153 CrossRef CAS.
- S. Garaj, S. Liu, J. A. Golovchenko and D. Branton, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 12192–12196 CrossRef CAS PubMed.
- K. Xiao, P. Giusto, L. Wen, L. Jiang and M. Antonietti, Angew. Chem., Int. Ed., 2018, 57, 10123–10126 CrossRef CAS PubMed.
- H. Gao, W. Chen, C. Xu, S. Liu, X. Tong and Y. Chen, Environ. Sci. Technol., 2020, 54, 2931–2940 CrossRef CAS PubMed.
- W. Guo, C. Cheng, Y. Wu, Y. Jiang, J. Gao, D. Li and L. Jiang, Adv. Mater., 2013, 25, 6064–6068 CrossRef CAS PubMed.
- L. Zhang, S. Zhou, L. Xie, L. Wen, J. Tang, K. Liang, X. Kong, J. Zeng, R. Zhang, J. Liu, B. Qiu, L. Jiang and B. Kong, Small, 2021, 17, 2100141 CrossRef CAS PubMed.
- Z. Zhang, P. Zhang, S. Yang, T. Zhang, M. Löffler, H. Shi, M. R. Lohe and X. Feng, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 13959–13966 CrossRef CAS PubMed.
- H. Cheng, Y. Zhou, Y. Feng, W. Geng, Q. Liu, W. Guo and L. Jiang, Adv. Mater., 2017, 29, 1700177 CrossRef PubMed.
- C. Zhu, P. Liu, B. Niu, Y. Liu, W. Xin, W. Chen, X.-Y. Kong, Z. Zhang, L. Jiang and L. Wen, J. Am. Chem. Soc., 2021, 143, 1932–1940 CrossRef CAS.
- G.-R. Xu, J.-M. Xu, H.-C. Su, X.-Y. Liu, L. Lu-Li, H.-L. Zhao, H.-J. Feng and R. Das, Desalination, 2019, 451, 18–34 CrossRef CAS.
- H. E. Karahan, K. Goh, C. Zhang, E. Yang, C. Yıldırım, C. Y. Chuah, M. G. Ahunbay, J. Lee, Ş. B. Tantekin-Ersolmaz, Y. Chen and T. Bae, Adv. Mater., 2020, 32, 1906697 CrossRef CAS.
- S. Hong, F. Ming, Y. Shi, R. Li, I. S. Kim, C. Y. Tang, H. N. Alshareef and P. Wang, ACS Nano, 2019, 13, 8917–8925 CrossRef CAS.
- J. Li, X. Li and B. Van der Bruggen, Environ. Sci.: Nano, 2020, 7, 1289–1304 RSC.
- C. E. Ren, K. B. Hatzell, M. Alhabeb, Z. Ling, K. A. Mahmoud and Y. Gogotsi, J. Phys. Chem. Lett., 2015, 6, 4026–4031 CrossRef CAS PubMed.
- Y. Zhu, S. Murali, W. Cai, X. Li, J. W. Suk, J. R. Potts and R. S. Ruoff, Adv. Mater., 2010, 22, 3906–3924 CrossRef CAS PubMed.
- Z. Jakšić and O. Jakšić, Biomimetics, 2020, 5, 24 CrossRef PubMed.
- T. Ma, E. Balanzat, J.-M. Janot and S. Balme, ACS Appl. Mater. Interfaces, 2019, 11, 12578–12585 CrossRef CAS.
- S. Hou, Q. Zhang, Z. Zhang, X. Kong, B. Lu, L. Wen and L. Jiang, Nano Energy, 2021, 79, 105509 CrossRef CAS.
- Y. Xu, Y. Song and F. Xu, Nano Energy, 2021, 79, 105468 CrossRef CAS.
- W. Chen, Q. Zhang, Y. Qian, W. Xin, D. Hao, X. Zhao, C. Zhu, X. Kong, B. Lu, L. Jiang and L. Wen, ACS Cent. Sci., 2020, 6, 2097–2104 CrossRef CAS PubMed.
- J.-M. Koo, C. H. Park, S. Yoo, G. W. Lee, S. Y. Yang, J. H. Kim and S. Il Yoo, Soft Matter, 2021, 17, 3700–3708 RSC.
- L. Wang, Z. Wang, S. K. Patel, S. Lin and M. Elimelech, ACS Nano, 2021, 15, 4093–4107 CrossRef CAS PubMed.
- C. Lin, C. Combs, Y. Su, L. Yeh and Z. S. Siwy, J. Am. Chem. Soc., 2019, 141, 3691–3698 CrossRef CAS PubMed.
- G. Pérez-Mitta, A. G. Albesa, C. Trautmann, M. E. Toimil-Molares and O. Azzaroni, Chem. Sci., 2017, 8, 890–913 RSC.
- Y. He, Z. Huang, B. Chen, M. Tsutsui, X. Shui Miao and M. Taniguchi, Sci. Rep., 2017, 7, 13156 CrossRef PubMed.
- B. D. Kang, H. J. Kim, M. G. Lee and D.-K. Kim, Energy, 2015, 86, 525–538 CrossRef CAS.
- Y. Zhang, Z. Huang, Y. He and X. Miao, Nanotechnology, 2019, 30, 428–429 Search PubMed.
- F. Yan, L. Yao, K. Chen, Q. Yang and B. Su, J. Mater. Chem. A, 2019, 7, 2385–2391 RSC.
- R. Long, M. Li, X. Chen, Z. Liu and W. Liu, Int. J. Heat Mass Transfer, 2021, 171, 121126 CrossRef CAS.
- L. Cao, F. Xiao, Y. Feng, W. Zhu, W. Geng, J. Yang, X. Zhang, N. Li, W. Guo and L. Jiang, Adv. Funct. Mater., 2017, 27, 1604302 CrossRef.
- Y.-S. Su, S.-C. Hsu, P.-H. Peng, J.-Y. Yang, M. Gao and L.-H. Yeh, Nano Energy, 2021, 84, 105930 CrossRef CAS.
- L. Cao, Q. Wen, Y. Feng, D. Ji, H. Li, N. Li, L. Jiang and W. Guo, Adv. Funct. Mater., 2018, 28, 1804189 CrossRef.
- K. Yazda, K. Bleau, Y. Zhang, X. Capaldi, T. St-Denis, P. Grutter and W. W. Reisner, Nano Lett., 2021, 21, 4152–4159 CrossRef CAS PubMed.
- J. Gao, X. Liu, Y. Jiang, L. Ding, L. Jiang and W. Guo, Small, 2019, 15, 1804279 CrossRef PubMed.
- W.-C. Huang and J.-P. Hsu, Electrochim. Acta, 2020, 353, 136613 CrossRef CAS.
- J.-P. Hsu, T.-C. Su, P.-H. Peng, S.-C. Hsu, M.-J. Zheng and L.-H. Yeh, ACS Nano, 2019, 13, 13374–13381 CrossRef CAS PubMed.
- L.-H. Yeh, F. Chen, Y.-T. Chiou and Y.-S. Su, Small, 2017, 13, 1702691 CrossRef PubMed.
- M. Graf, M. Lihter, D. Unuchek, A. Sarathy, J.-P. Leburton, A. Kis and A. Radenovic, Joule, 2019, 3, 1549–1564 CrossRef CAS.
- K. Xiao, P. Giusto, F. Chen, R. Chen, T. Heil, S. Cao, L. Chen, F. Fan and L. Jiang, Natl. Sci. Rev., 2021, 8(8), nwaa231 CrossRef.
- P. Liu, T. Zhou, Y. Teng, L. Fu, Y. Hu, X. Lin, X.-Y. Kong, L. Jiang and L. Wen, CCS Chem., 2020, 1325–1335 Search PubMed.
- L.-H. Yeh, Z.-Y. Huang, Y.-C. Liu, M.-J. Deng, T.-H. Chou, H.-C. Ou Yang, T. Ahamad, S. M. Alshehri and K. C.-W. Wu, J. Mater. Chem. A, 2019, 7, 26791–26796 RSC.
- S. Balme, T. Ma, E. Balanzat and J. Janot, J. Membr. Sci., 2017, 544, 18–24 CrossRef CAS.
- K. H. Lee, H. Park, W. Eom, D. J. Kang, S. H. Noh and T. H. Han, J. Mater. Chem. A, 2019, 7, 23727–23732 RSC.
- M. Khatibi, A. Sadeghi and S. N. Ashrafizadeh, Phys. Chem. Chem. Phys., 2021, 23, 2211–2221 RSC.
- Z. Zhang, S. Yang, P. Zhang, J. Zhang, G. Chen and X. Feng, Nat. Commun., 2019, 10, 2920 CrossRef PubMed.
- Z. Zhang, X. Sui, P. Li, G. Xie, X. Y. Kong, K. Xiao, L. Gao, L. Wen and L. Jiang, J. Am. Chem. Soc., 2017, 139, 8905–8914 CrossRef CAS PubMed.
- H.-C. Yang, Y. Xie, J. Hou, A. K. Cheetham, V. Chen and S. B. Darling, Adv. Mater., 2018, 30, 1801495 CrossRef PubMed.
- H. Li, F. Xiao, G. Hong, J. Su, N. Li, L. Cao, Q. Wen and W. Guo, Chin. J. Chem., 2019, 37, 469–473 CrossRef CAS.
- S. Lee, H. Kim and D.-K. Kim, Energies, 2016, 9, 49 CrossRef.
- J. Hwang, S. Kataoka, A. Endo and H. Daiguji, Lab Chip, 2016, 16, 3824–3832 RSC.
- M. Tagliazucchi, O. Azzaroni and I. Szleifer, J. Am. Chem. Soc., 2010, 132, 12404–12411 CrossRef CAS PubMed.
- Z. Siwy, I. D. Kosińska, A. Fuliński and C. R. Martin, Phys. Rev. Lett., 2005, 94, 048102 CrossRef CAS PubMed.
- R. Long, Z. Kuang, Z. Liu and W. Liu, Phys. Chem. Chem. Phys., 2018, 20, 7295–7302 RSC.
- J. Cervera, B. Schiedt, R. Neumann, S. Mafé and P. Ramírez, J. Chem. Phys., 2006, 124, 104706 CrossRef PubMed.
- R. Li, J. Jiang, Q. Liu, Z. Xie and J. Zhai, Nano Energy, 2018, 53, 643–649 CrossRef CAS.
- J. Gao, W. Guo, D. Feng, H. Wang, D. Zhao and L. Jiang, J. Am. Chem. Soc., 2014, 136, 12265–12272 CrossRef CAS PubMed.
- L. Cao, W. Guo, W. Ma, L. Wang, F. Xia, S. Wang, Y. Wang, L. Jiang and D. Zhu, Energy Environ. Sci., 2011, 4, 2259–2266 RSC.
- H. Zhang, J. Hou, Y. Hu, P. Wang, R. Ou, L. Jiang, J. Z. Liu, B. D. Freeman, A. J. Hill and H. Wang, Sci. Adv., 2018, 4, eaaq0066 CrossRef PubMed.
- J. Lu, H. Zhang, J. Hou, X. Li, X. Hu, Y. Hu, C. D. Easton, Q. Li, C. Sun, A. W. Thornton, M. R. Hill, X. Zhang, G. Jiang, J. Z. Liu, A. J. Hill, B. D. Freeman, L. Jiang and H. Wang, Nat. Mater., 2020, 19, 767–774 CrossRef CAS PubMed.
- X. Li, H. Zhang, P. Wang, J. Hou, J. Lu, C. D. Easton, X. Zhang, M. R. Hill, A. W. Thornton, J. Z. Liu, B. D. Freeman, A. J. Hill, L. Jiang and H. Wang, Nat. Commun., 2019, 10, 2490 CrossRef PubMed.
- Y.-C. Liu, L.-H. Yeh, M.-J. Zheng and K. C.-W. Wu, Sci. Adv., 2021, 7, eabe9924 CAS.
- R. Long, Z. Kuang, Z. Liu and W. Liu, J. Membr. Sci., 2018, 561, 1–9 CrossRef CAS.
- Y. Fu, X. Guo, Y. Wang, X. Wang and J. Xue, Nano Energy, 2019, 57, 783–790 CrossRef CAS.
- J. Hwang, T. Sekimoto, W.-L. Hsu, S. Kataoka, A. Endo and H. Daiguji, Nanoscale, 2017, 9, 12068–12076 RSC.
- Y. Wu, W. Xin, X.-Y. Kong, J. Chen, Y. Qian, Y. Sun, X. Zhao, W. Chen, L. Jiang and L. Wen, Mater. Horiz., 2020, 7, 2702–2709 RSC.
- R. Long, Z. Kuang, Z. Liu and W. Liu, Natl. Sci. Rev., 2019, 6, 1266–1273 CrossRef.
- V.-P. Mai and R.-J. Yang, Appl. Energy, 2020, 274, 115294 CrossRef CAS.
- K. Chen, L. Yao, F. Yan, S. Liu, R. Yang and B. Su, J. Mater. Chem. A, 2019, 7, 25258–25261 RSC.
- A. Tamburini, M. Tedesco, A. Cipollina, G. Micale, M. Ciofalo, M. Papapetrou, W. Van Baak and A. Piacentino, Appl. Energy, 2017, 206, 1334–1353 CrossRef CAS.
- Z. Zhang, W. Shen, L. Lin, M. Wang, N. Li, Z. Zheng, F. Liu and L. Cao, Adv. Sci., 2020, 7, 2000286 CrossRef CAS PubMed.
- C. Wu, T. Xiao, J. Tang, Q. Zhang, Z. Liu, J. Liu and H. Wang, Nano Energy, 2020, 76, 105113 CrossRef CAS.
- M. I. Walker, K. Ubych, V. Saraswat, E. A. Chalklen, P. Braeuninger-Weimer, S. Caneva, R. S. Weatherup, S. Hofmann and U. F. Keyser, ACS Nano, 2017, 11, 1340–1346 CrossRef CAS.
- W. Xin, H. Xiao, X.-Y. Kong, J. Chen, L. Yang, B. Niu, Y. Qian, Y. Teng, L. Jiang and L. Wen, ACS Nano, 2020, 14, 9701–9710 CrossRef CAS PubMed.
- X. Zhu, Y. Zhou, J. Hao, B. Bao, X. Bian, X. Jiang, J. Pang, H. Zhang, Z. Jiang and L. Jiang, ACS Nano, 2017, 11, 10816–10824 CrossRef CAS PubMed.
- C. Chen, D. Liu, G. Yang, J. Wang, L. Wang and W. Lei, Adv. Energy Mater., 2020, 10, 1904098 CrossRef CAS.
- M. Naguib, M. Kurtoglu, V. Presser, J. Lu, J. Niu, M. Heon, L. Hultman, Y. Gogotsi and M. W. Barsoum, Adv. Mater., 2011, 23, 4248–4253 CrossRef CAS PubMed.
- V. M. Hong Ng, H. Huang, K. Zhou, P. S. Lee, W. Que, J. Z. Xu and L. B. Kong, J. Mater. Chem. A, 2017, 5, 3039–3068 RSC.
- P. Liu, Y. Sun, C. Zhu, B. Niu, X. Huang, X.-Y. Kong, L. Jiang and L. Wen, Nano Lett., 2020, 20, 3593–3601 CrossRef CAS.
- S. Qin, D. Liu, Y. Chen, C. Chen, G. Wang, J. Wang, J. M. Razal and W. Lei, Nano Energy, 2018, 47, 368–373 CrossRef CAS.
- C. Chen, D. Liu, X. Qing, G. Yang, X. Wang and W. Lei, ACS Appl. Mater. Interfaces, 2020, 12, 52771–52778 CrossRef CAS PubMed.
- X. Zhu, J. Zhong, J. Hao, Y. Wang, J. Zhou, J. Liao, Y. Dong, J. Pang, H. Zhang, Z. Wang, W. Zhang, W. Zheng, Z. Jiang, Y. Zhou and L. Jiang, Adv. Energy Mater., 2020, 10, 2001552 CrossRef CAS.
- Y. Sun, T. Dong, C. Lu, W. Xin, L. Yang, P. Liu, Y. Qian, Y. Zhao, X. Kong, L. Wen and L. Jiang, Angew. Chem., Int. Ed., 2020, 59, 17423–17428 CrossRef CAS PubMed.
- W. Chen, Q. Wang, J. Chen, Q. Zhang, X. Zhao, Y. Qian, C. Zhu, L. Yang, Y. Zhao, X.-Y. Kong, B. Lu, L. Jiang and L. Wen, Nano Lett., 2020, 20, 5705–5713 CrossRef CAS.
- J. Lu, H. Zhang, X. Hu, B. Qian, J. Hou, L. Han, Y. Zhu, C. Sun, L. Jiang and H. Wang, ACS Nano, 2021, 15, 1240–1249 CrossRef CAS PubMed.
- S. Hou, W. Ji, J. Chen, Y. Teng, L. Wen and L. Jiang, Angew. Chem., Int. Ed., 2021, 60, 9925–9930 CrossRef CAS PubMed.
- X. Zhao, C. Lu, L. Yang, W. Chen, W. Xin, X.-Y. Kong, Q. Fu, L. Wen, G. Qiao and L. Jiang, Nano Energy, 2021, 81, 105657 CrossRef CAS.
- S. Zhou, L. Xie, L. Zhang, L. Wen, J. Tang, J. Zeng, T. Liu, D. Peng, M. Yan, B. Qiu, Q. Liang, K. Liang, L. Jiang and B. Kong, ACS Appl. Mater. Interfaces, 2021, 13, 8782–8793 CrossRef CAS PubMed.
- S. H. Kwak, S.-R. Kwon, S. Baek, S.-M. Lim, Y.-C. Joo and T. D. Chung, Sci. Rep., 2016, 6, 26416 CrossRef CAS PubMed.
- X. Sui, Z. Zhang, C. Li, L. Gao, Y. Zhao, L. Yang, L. Wen and L. Jiang, ACS Appl. Mater. Interfaces, 2019, 11, 23815–23821 CrossRef CAS PubMed.
- T. Xiao, Q. Zhang, J. Jiang, J. Ma, Q. Liu, B. Lu, Z. Liu and J. Zhai, Energy Technol., 2018, 7, 1800952 CrossRef.
- A. Pendse, S. Cetindag, P. Rehak, S. Behura, H. Gao, N. H. L. Nguyen, T. Wang, V. Berry, P. Král, J. Shan and S. Kim, Adv. Funct. Mater., 2021, 2009586 CrossRef CAS.
- L. Xie, S. Zhou, J. Liu, B. Qiu, T. Liu, Q. Liang, X. Zheng, B. Li, J. Zeng, M. Yan, Y. He, X. Zhang, H. Zeng, D. Ma, P. Chen, K. Liang, L. Jiang, Y. Wang, D. Zhao and B. Kong, J. Am. Chem. Soc., 2021, 143, 6922–6932 CrossRef CAS PubMed.
- W. Xin, Z. Zhang, X. Huang, Y. Hu, T. Zhou, C. Zhu, X. Kong, L. Jiang and L. Wen, Nat. Commun., 2019, 10, 3876 CrossRef PubMed.
- K. Kwon, S. J. Lee, L. Li, C. Han and D. Kim, Int. J. Energy Res., 2014, 38, 530–537 CrossRef CAS.
- Z. Zhang, X. Y. Kong, K. Xiao, Q. Liu, G. Xie, P. Li, J. Ma, Y. Tian, L. Wen and L. Jiang, J. Am. Chem. Soc., 2015, 137, 14765–14772 CrossRef CAS PubMed.
- Q.-Y. Wu, C. Wang, R. Wang, C. Chen, J. Gao, J. Dai, D. Liu, Z. Lin and L. Hu, Adv. Energy Mater., 2019, 10, 1902590 CrossRef.
- D. A. Vermaas, J. Veerman, M. Saakes and K. Nijmeijer, Energy Environ. Sci., 2014, 7, 1434–1445 RSC.
- O. Schaetzle and C. J. N. Buisman, Engineering, 2015, 1, 164–166 CrossRef.
- D. A. Vermaas, D. Kunteng, J. Veerman, M. Saakes and K. Nijmeijer, Environ. Sci. Technol., 2014, 48, 3065–3073 CrossRef CAS PubMed.
- F. Kotoka, I. Merino-Garcia and S. Velizarov, Membranes, 2020, 10, 160 CrossRef CAS.
- D. Pintossi, M. Saakes, Z. Borneman and K. Nijmeijer, ACS Appl. Mater. Interfaces, 2021, 13, 18348–18357 CrossRef CAS PubMed.
- R. A. Tufa, E. Rugiero, D. Chanda, J. Hnàt, W. van Baak, J. Veerman, E. Fontananova, G. Di Profio, E. Drioli, K. Bouzek and E. Curcio, J. Membr. Sci., 2016, 514, 155–164 CrossRef CAS.
- R. A. Tufa, J. Hnát, M. Němeček, R. Kodým, E. Curcio and K. Bouzek, J. Cleaner Prod., 2018, 203, 418–426 CrossRef CAS.
- X. Chen, C. Jiang, Y. Zhang, Y. Wang and T. Xu, J. Membr. Sci., 2017, 544, 397–405 CrossRef CAS.
- X. Chen, C. Jiang, M. A. Shehzad, Y. Wang, H. Feng, Z. Yang and T. Xu, ACS Sustainable Chem. Eng., 2019, 7, 13023–13030 CrossRef CAS.
- J.-Y. Nam, R. D. Cusick, Y. Kim and B. E. Logan, Environ. Sci. Technol., 2012, 46, 5240–5246 CrossRef CAS PubMed.
- X. Li, I. Angelidaki and Y. Zhang, Water Res., 2018, 142, 396–404 CrossRef CAS PubMed.
- Y. Kim and B. E. Logan, Environ. Sci. Technol., 2011, 45, 5834–5839 CrossRef CAS PubMed.
- X. Zhu, T. Kim, M. Rahimi, C. A. Gorski and B. E. Logan, ChemSusChem, 2017, 10, 797–803 CrossRef CAS PubMed.
- J.-H. Kim, J.-H. Lee, S. Maurya, S.-H. Shin, J.-Y. Lee, I. S. Chang and S.-H. Moon, Electrochem. Commun., 2016, 72, 157–161 CrossRef CAS.
- W. J. van Egmond, M. Saakes, S. Porada, T. Meuwissen, C. J. N. Buisman and H. V. M. Hamelers, J. Power Sources, 2016, 325, 129–139 CrossRef CAS.
- F. E. Ahmed, R. Hashaikeh and N. Hilal, Desalination, 2020, 495, 114659 CrossRef CAS.
- K. Kwon, J. Han, B. H. Park, Y. Shin and D. Kim, Desalination, 2015, 362, 1–10 CrossRef CAS.
- R. A. Tufa, Y. Noviello, G. Di Profio, F. Macedonio, A. Ali, E. Drioli, E. Fontananova, K. Bouzek and E. Curcio, Appl. Energy, 2019, 253, 113551 CrossRef CAS.
- W. Li, W. B. Krantz, E. R. Cornelissen, J. W. Post, A. R. D. Verliefde and C. Y. Tang, Appl. Energy, 2013, 104, 592–602 CrossRef CAS.
- A. Zoungrana and M. Çakmakci, Int. J. Energy Res., 2021, 45, 3495–3522 CrossRef.
- C. Tristán, M. Rumayor, A. Dominguez-Ramos, M. Fallanza, R. Ibáñez and I. Ortiz, Sustainable Energy Fuels, 2020, 4, 4273–4284 RSC.
- R. A. Tufa, E. Curcio, E. Brauns, W. van Baak, E. Fontananova and G. Di Profio, J. Membr. Sci., 2015, 496, 325–333 CrossRef CAS.
- X. Luo, X. Cao, Y. Mo, K. Xiao, X. Zhang, P. Liang and X. Huang, Electrochem. Commun., 2012, 19, 25–28 CrossRef CAS.
- R. Long, B. Li, Z. Liu and W. Liu, J. Membr. Sci., 2017, 525, 107–115 CrossRef CAS.
- M. Papapetrou, G. Kosmadakis, F. Giacalone, B. Ortega-Delgado, A. Cipollina, A. Tamburini and G. Micale, Energies, 2019, 12, 3206 CrossRef CAS.
- D. A. Vermaas, E. Guler, M. Saakes and K. Nijmeijer, Energy Procedia, 2012, 20, 170–184 CrossRef CAS.
- E. Brauns, Desalination, 2008, 219, 312–323 CrossRef CAS.
- O. Scialdone, A. D'Angelo, E. De Lumè and A. Galia, Electrochim. Acta, 2014, 137, 258–265 CrossRef CAS.
- O. Scialdone, A. D'Angelo and A. Galia, J. Electroanal. Chem., 2015, 738, 61–68 CrossRef CAS.
- J. Chen, W. Xin, X.-Y. Kong, Y. Qian, X. Zhao, W. Chen, Y. Sun, Y. Wu, L. Jiang and L. Wen, ACS Energy Lett., 2020, 5, 742–748 CrossRef CAS.
- L. Fu, J. Jiang, B. Lu, Y. Xu and J. Zhai, ChemNanoMat, 2019, 5, 1182–1187 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2021 |