Open Access Article
Open Access ArticleStructural strategy for advancing nonlinear optical effects in 1D-[MX2]∞ chains: internal distortion and atomic types
Chaoyi Zhu *ab
*ab
aShanghai Compulsory Verification Center for Measuring Instrument, Shanghai Institute of Measurement and Testing Technology, Shanghai 200233, P. R. China. E-mail: m040120320@sues.edu.cn
bSchool of Chemistry and Chemical Engineering, Shanghai University of Engineering Science, Shanghai 201620, P. R. China
First published on 24th May 2024
Abstract
This work aimed to alleviate the limitations of existing mid-infrared nonlinear-optics (MIR-NLO) crystals by conducting theoretical research on 1D-[MX2]∞ (1D = one-dimensional; M = metallic element; X = anionic element) structures in relation to NLO. An analysis was conducted on the electronic structure and optical properties of six selenides (BaZnGeSe4, KxBa1−x/2Ga2Se4, KxBa1−x/2GayIn2−ySe4, KxBa1−x/2In2Se4, BaZnSiSe4, SrZnSiSe4) and three arsenides (Cs2SnAs2, Rb2SnAs2, K2SnAs2) using first principles. Afterwards, the inherent characteristics of these 1D-[MX2]∞ chains were further examined. The calculation results suggest that the presence of internal distortion (non-centrosymmetric) and high electronegativity in M elements can greatly enhance the NLO capability of 1D-[MX2]∞ structures. Furthermore, the first-ever prediction of K2SnAs2's NLO ability has been made. Ultimately, the establishment of a theoretical structure (K2BaSn2As4) provides guidance for the subsequent creation of high-performance MIR-NLO crystals.
1 Introduction
Measurement and testing are essential prerequisites for the advancement of any nation, particularly in highly precise scientific domains. MIR lasers have exhibited significant luminosity in metrology domains, including chemical composition analysis, medical surgical procedures, and radar detection.1–3 The quality of MIR-NLO crystals, which serve as the fundamental element for converting laser frequency, has a significant impact on the measurement accuracy of the entire laser system. The predominant commercially available MIR-NLO crystals on a large scale consist primarily of diamond-like structures or perovskite structures, such as AgGaS2 (AGS), AgGaSe2, GaAs, LiNbO3, and so on.4–7 Advancements in synthesis technology and theory have led to the successful production of an increasing number of MIR-NLO crystals with distinctive characteristics, including InGa2Cl7, MoO2Cl2, NaMg3Ga3Se8, KYGeS4, and others.8–11 Several new generation MIR-NLO crystals, including Li1−xAgxGaSe2, BaGe4Se7, La3Nb0.5Ga5.5O14, and others, have been progressively utilized in industrial production and practical applications.12–14Considering the increasing demand for high-performance MIR-NLO crystals, it is necessary to conduct first-principles research on materials. Alongside traditional research on electronic orbitals, recent years have witnessed the emergence of various sophisticated chemical computing software.15 The rapid strides in computer science have propelled the development of high-throughput screening and material design, facilitating a more seamless integration of theoretical insights and experimental endeavors. Therefore, future material synthesis endeavors are poised to be more precise, leading to significant reductions in research time.
In recent years, a plethora of reports underscore the significance and triumphs of cutting-edge technology. Notably, advanced deep ultraviolet borate crystals have undergone meticulous screening using the Inorganic-Crystal-Structure-Database (ICSD).16 Moreover, a systematic theoretical analysis has delved into the intrinsic correlation between crystal structure and birefringence.17 Optical theoretical structure prediction stands out as the forefront of NLO advancements, primarily lauded for its efficacy in augmenting experimental success rates.18 A striking example is the recent success story of NaSrBS3, the pioneer material predicted within the thioborate domain, thanks to refined theoretical guidance.19 In addition to the aforementioned borate/thioborate, this technology extends its reach into the realm of chalcogenides. Noteworthy theoretical inquiries have unfolded regarding the crystal structure and synthesis pathways of LiGaSe2, including theoretical predictions and successful preparation of MgGa2Se4.20,21 In addition, with the support of classical molecular dynamics, Density-Functional-Theory and other theories, significant breakthroughs have also been made in the field of organic luminescent molecules in recent times.22
In 2022, extensive theoretical research elucidated the crystal structure of 1D functional modules [BO2]∞ chains within the domain of deep ultraviolet NLO.23 These reports underscored the dynamic and thermodynamic stability of these theoretical crystals. Subsequently, in 2024, the successful synthesis of two high-quality NLO materials, NaLu(SeO3)2 and Cs3In(In4Se7)(P2Se6), based on theoretical designs, marked significant advancements.24,25 Notably, the prediction and realization of optical properties in nanoscale thin film materials further underscore the critical role of theoretical design in shaping the future exploration of NLO materials.26
Beyond NLO, the integration of theoretical research into practical experimentation has reached a notable maturity, particularly evident in the medical domain.27 In addition, the exploration of the superposition effect among two-dimensional layers, amalgamating theoretical analysis with experimental methodologies, has garnered widespread recognition, especially in the study of optics and topological structures.28 Noteworthy is the successful prediction, through optical theory research, of the fluorescence capabilities of periodically stacked photonic crystal plates.29 These reports underscore the paramount importance of theoretical predictions in various chemical fields.
Among these NLO systems, the MIR-NLO ability of the AII–MII–MIV–Ch (AII = alkaline earth metal element; MII = +2 valence metal element; MIV = +4 valence metal element; Ch = S, Se, Te) system has recently been extensively investigated. Several optical materials with exceptional performance are currently being investigated. Sulfides like SrMgGeS4, SrCdSiS4, and SrZnGeS4 exhibit extremely large band gap (Egap) values and laser damage threshold (LDT).30–32 Selenides such as BaHgGeSe4, SrHgGeSe4, and SrHgSnSe4 demonstrate pronounced second harmonic generation (SHG) characteristics.33,34 The 1D-[MX2]∞ structure in this series of materials consistently achieves a favourable equilibrium between SHG and LDT. Both BaZnGeSe4 and BaZnSiSe4 exhibit wide Egap values and possess strong SHG properties.35 In particular, the SrZnSiSe4 possesses a 2 × SHG and a 10 × LDT for AGS.36
Furthermore, alongside AII–MII–MIV–Ch, a group of 1D-NLO materials containing AI–AII–MIII–Se (AI = alkali metal element; MIII = +3 valence metal element) has been recently synthesized with great success.37 The shared structural characteristic among AII–MII–MIV–Ch and AI–AII–MIII–Se is the existence of 1D-[MX2]∞ chains.38 AI–AII–MIII–Se contain a greater amount of alkaline ions compared to AII–MII–MIV–Ch, making it a variant structure. The alteration in the structure has resulted in a rise in the A/M (A = alkali metal element and alkaline earth metal element) value. The precise methodology for calculating A/M has been elucidated in pertinent reports.39 It is worth noting that among these 1D materials, KxBa1−x/2Ga2Se4 demonstrates excellent NLO ability, with a SHG of 1 × AGS and a LDT of 13.4 × AGS. It is evident that 1D-[MX2]∞ chains possess significant research value in the field of NLO.40
The primary obstacle faced by current optical parametric oscillation (OPO) MIR lasers is the insufficient output energy of idle light, while attempts to enhance the energy of pump light often result in the fragmentation of MIR-NLO crystals.41 Furthermore, the majority of MIR lasers are constrained by phase matching in MIR-NLO crystals, thereby rendering them incapable of producing precise wavelengths of MIR light.42 Hence, a superior MIR-NLO crystal typically necessitates the presence of several optical indicators, including robust nonlinear coefficients, high LDT, suitable phase matching, and sufficiently low absorption bands.43
Non-centrosymmetric tetra-coordinated phosphorus (Pn; Pn = P, As) compounds are widely recognized as a highly sought-after category of optical materials.44 This is primarily attributed to their exceptional upper limit in nonlinear coefficients. The ZnGeP2 crystal currently in use has a nonlinear coefficient of 70 pm V−1, which is five times higher than that of AGS. Additionally, its LDT is about three times greater than AGS.45 The CdSiP2 crystal is extensively utilized in medical devices for its capacity to produce intense MIR light at approximately 6200 nm.46 Furthermore, individuals have progressively uncovered a significant quantity of tetra-coordinated Pn-NLO materials that exhibit exceptional performance. Mg2In3Si2P7, MgSiP2, and BaGe2P2 are examples of high-performance NLO materials that have garnered significant interest.47–49 Ba2Si3P6 exhibits high LDT and facilitates the growth of large single crystals in the context of 1D structure.50 The aforementioned diverse situations clearly showcase the exceptional characteristics of [MPn4] in the realm of MIR-NLO.
Pn materials also contain an extensive variety of 1D-[MX2]∞ chains, including K2SiP2, Na2SiP2 and others.51–53 Regrettably, the majority of these structures exhibit centrosymmetry and lack the capacity for second-order polarization. Consequently, it is critical to investigate the optical properties of [MPn4] in MIR-NLO, specifically in 1D-[MX2]∞ chains. This study commenced by conducting a systematic analysis of six existing 1D-[MSe2]∞ structures (BaZnGeSe4, KxBa1−x/2Ga2Se4, KxBa1−x/2GayIn2−ySe4, KxBa1−x/2In2Se4, BaZnSiSe4, SrZnSiSe4). The optical properties and electronic structure of the subject were examined by employing first principles. Furthermore, this study provided the first-ever prediction of the NLO capability of K2SnAs2 by analysing the electronic structures of three 1D-[SnAs2]∞ materials (Cs2SnAs2, Rb2SnAs2, K2SnAs2).54,55 This work systematically clarifies the diverse impacts of structural modifications on the optical properties of 1D-[MX2]∞ chains through the construction of a theoretical structure (K2BaSn2As4). This theoretical investigation has the potential to offer adequate structural theoretical backing for the fabrication of MIR-NLO crystals of superior quality.
2 Computational methods
The open-source computing software “Abinit” is well-known for its high computational accuracy and extensive functionality. The ground state Bloch wavefunctions utilized in this study were acquired via “Abinit”, with the Perdew–Burke–Ernzerhof (PBE) functional serving as the pseudopotential.56–59 PBE functional offers enhanced precision in delineating the wavefunction across the entirety of a crystal structure, particularly in capturing high-order derivatives of the wavefunction. The calculation of all ground state Bloch wavefunctions utilised the k-points of 4 × 4 × 4 and the cut-off energy of 2200 eV.60,61 The primary approach used to derive Partial Density of States (PDOS) values is via the Projector-Augmented-Wave (PAW) method, which involves the individual calculation of atoms.62 The calculation of linear optics and NLO is performed utilizing the Independent-Particle-Approximation (IPA) theory.63 The number of conduction bands utilized in optical response calculations is typically two to three times greater than the number of valence bands. Other structures were evaluated using optical band gap (Eopt) values as scissors, whereas K2SnAs2 and K2BaSn2As4 were evaluated using Heyd–Scuseria–Ernzerhof band gap (EHSE06) values as scissors.64 All calculated structures have been optimized, and the stress tolerance has been set to 2.5 × 10−3 eV Å−1.65,66 The maximum number of iterations for all calculations is capped at 200. In the calculation of PDOS, the smear value is set to more than 10 times the default value. The structural optimization part mainly adopts the Broyden–Fletcher–Goldfarb–Shanno (BFGS) minimization method. In the process of calculating dipole hyperpolarizability and first dipole hyperpolarizability using “Gaussian”, B3LYP functional and LanL2DZ basis set were adopted. In all calculation processes, the remaining calculation parameters are set to default values.67–69 The calculated data is processed using recognized methods.The calculation method for the effective nonlinear coefficient (deff) is:70
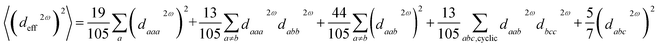 | (1) |
The calculation method for the dipole hyperpolarizability difference (Δα) is:71
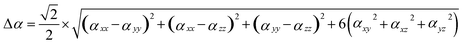 | (2) |
The calculation method for the total first dipole hyperpolarizability (βtot) is:72
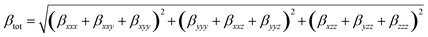 | (3) |
3 Theoretical structure
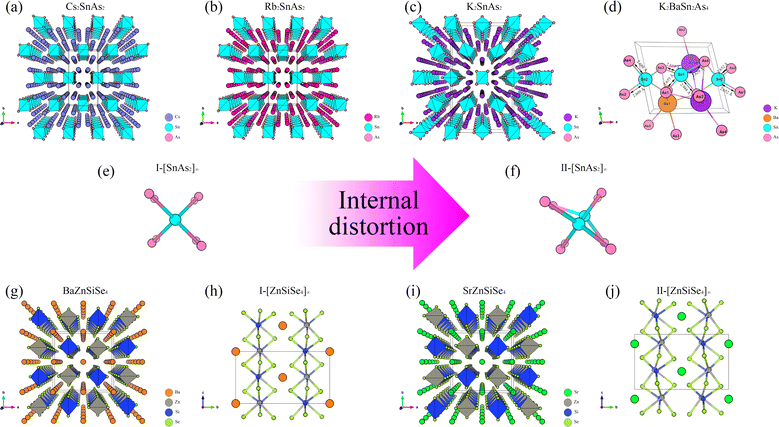
From the perspective of NLO, constructing a 1D-[MX2]∞ chain with excellent NLO capability often requires a high degree of consistency in the [MX4] arrangement. In theory, such a structure would polarize the electron gas in one direction, producing significant NLO capabilities. Therefore, in the process of constructing theoretical crystals, it is advisable to have only one 1D-[MX2]∞ chain wherever feasible. In other words, the simpler the structure of the non centrosymmetric theoretical crystal, the better. In addition, considering the excellent NLO performance of non-centrosymmetric Pn materials, it is necessary to use [MPn4]. The above two points are the core ideas for constructing theoretical crystals, and additional attention should be paid to maintaining charge balance during this process.Presently, centrosymmetric structures constitute the overwhelming majority of 1D-[MPn2]∞ structures uncovered (Fig. 1 and 2). To elucidate the relationship between the internal configuration and optical properties of 1D-[MPn2]∞ chains in their entirety, it is necessary to introduce a theoretical framework. In addition to conducting theoretical analyses of established 1D-[SnAs2]∞ structures, this work also develops a novel theoretical crystal structure. The artificial distortion within the 1D-[SnAs2]∞ chain primarily constitutes this theoretical structure. By introducing K × 2, Ba × 1, Sn × 2, As × 4 into a simple cube (P1) in order to achieve charge balance within the system. Next, establish the coordinates (0.500, 0.535, 0.535) and (0.000, 0.465, 0.465) for the two Sn atoms. Conduct structural optimization while accounting for variations in cell shape and the displacement of other ions, while disregarding symmetry (Fig. 2e and f). In conclusion, a theoretical auxiliary structure denoted as K2BaSn2As4 (Cm) was acquired, representing the entire system with an absolute energy of around 3489.76 eV (Fig. 2d). Tables 1 and 2 present the lattice parameters and atomic coordinates pertaining to the theoretical structure.
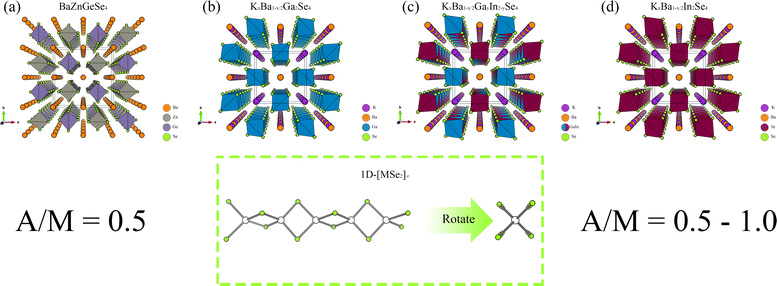 | ||
| Fig. 1 (a)–(d) The crystal structures of BaZnGeSe4, KxBa1−x/2Ga2Se4, KxBa1−x/2GayIn2−ySe4, and KxBa1−x/2In2Se4, as well as the arrangement of their 1D chains. | ||
| Atom | x | y | z |
|---|---|---|---|
| K | −0.06756 | 0.21776 | 0.67958 |
| Ba | 0.09628 | 0.00000 | 0.21394 |
| Sn1 | 0.53500 | 0.00000 | 0.50000 |
| Sn2 | 0.46500 | 0.00000 | 0.00000 |
| As1 | 0.45759 | 0.18175 | 0.24359 |
| As2 | 0.24093 | 0.00000 | 0.65981 |
| As3 | 0.73448 | 0.00000 | 0.85842 |
| Chemical bond | Bond length |
|---|---|
| Sn1–As1 | 2.65543 Å |
| Sn1–As2 | 2.94772 Å |
| Sn1–As3 | 2.62890 Å |
| Sn2–As1 | 2.65237 Å |
| Sn2–As2 | 2.60882 Å |
| Sn3–As3 | 2.67987 Å |
4 Electronic structure
4.1 Band structure
A systematic analysis of the electronic structures of these 1D crystals was conducted utilizing first principles methods. Its low Egap value and direct band gap semiconductor nature are both inferred from the band structure of BaZnGeSe4 (Fig. 3a). The band structure takes on an entirely new appearance as a result of the adjustment of A/M. The indirect band gap semiconductors denoted as KxBa1−x/2Ga2Se4, KxBa1−x/2GayIn2−ySe4, and KxBa1−x/2In2Se4 exhibit a decreasing order of Egap values (Fig. 3b–d). In contrast, their Eopt and Egap values exhibit a diametrically opposed trend, which is consistent with the findings of this article's calculations.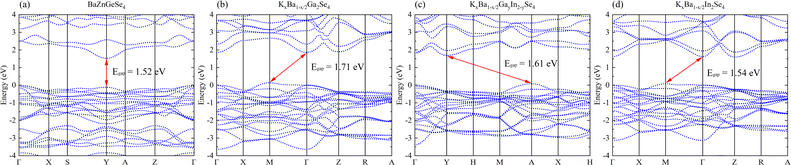 | ||
| Fig. 3 (a)–(d) The band structures of BaZnGeSe4, KxBa1−x/2Ga2Se4, KxBa1−x/2GayIn2−ySe4, and KxBa1−x/2In2Se4. | ||
Cs2SnAs2 and Rb2SnAs2, which are both centrally symmetric 1D crystals, both have indirect band gap semiconductor characteristics (Fig. 4a and b). Although their structures are virtually identical, Rb2SnAs2 has a slightly lower Egap value than Cs2SnAs2. When the radius of alkali metals decreases, the inter-crystal gaps become inadequate for the preservation of the space group of Ibam. At this juncture, the configuration of these 1D-[SnAs2]∞ chains has undergone a transformation, as has the configuration of K2SnAs2 (C222). The atomic configuration in question exhibits characteristics reminiscent of a trigonal system, thereby liberating it from the electronic confines imposed by indirect band gap. The calculation results indicate that the Egap value of K2SnAs2 is approximately 0.81 eV, which is higher than the Egap values of Rb2SnAs2 and Cs2SnAs2 (Fig. 4c). The fundamental reason for such differences may come from the symmetry of the crystal, which changes the energy at point Z and causes Fermi level (EF) to regress to Γ Near the point.
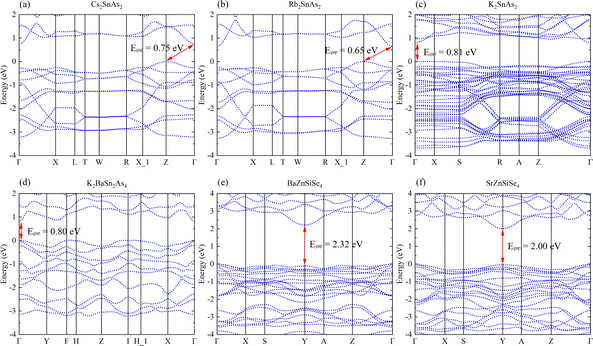 | ||
| Fig. 4 (a)–(f) The band structures of Cs2SnAs2, Rb2SnAs2, K2SnAs2, K2BaSn2As4, BaZnSiSe4, and SrZnSiSe4. | ||
K2BaSn2As4 lacks an indirect band gap across the entirety of the energy space, with an estimated Egap value of 0.80 eV (Fig. 4d). This is very close to the Egap value of K2SnAs2. Therefore, 1D chains may primarily regulate the Egap value of this direct band gap structure. The Egap value of BaZnSiSe4 possessing a 1D-[MSe2]∞ structure is approximately 0.32 eV greater than that of SrZnSiSe4 (Fig. 4e and f). Both substances have direct band gap semiconductor characteristics, with their EF situated in close proximity to the Y point. The computed values of these band structures exhibit a high degree of congruence with the computed values documented in the scientific literature.
Research on 1D-[SnAs2]∞ and 1D-[ZnSiSe4]∞ indicates that in similar 1D-[MX2]∞ structures, the Egap value typically decreases with a decrease in the AI/AII ions radius. This may indicate that the stronger the electronegativity of AI/AII ions, the higher the Egap value of the material. In addition, combining the calculation results in Fig. 3 and 4, it can be found that the Egap value of the 1D-[MX2]∞ structure is mostly dominated by the electronegativity difference between the M–X bonds, with the electronegativity potency of AI/AII ions following closely behind.
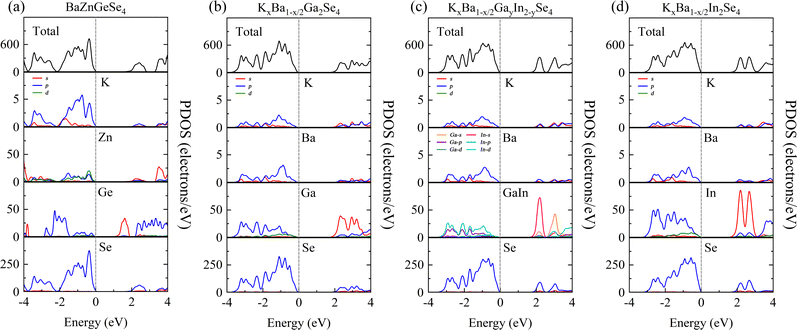
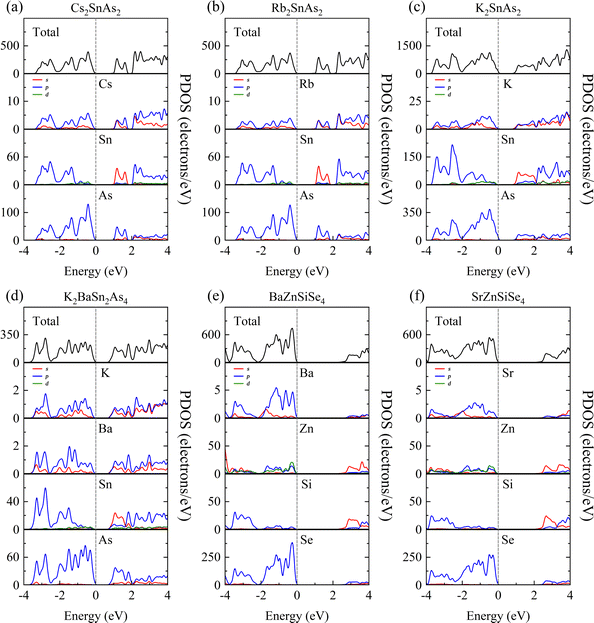
4.2 Orbital structure
The purpose of this calculation was to perform a more comprehensive analysis of the electronic structures of these 1D structures. Zn-3d orbital electrons engage in valence band bonding in close proximity to the EF of BaZnGeSe4, whereas Ge-4s orbital electrons are involved in conduction band bonding (Fig. 5a). From the PDOS of AI-AII–MIII–Se, some rules regarding the Egap value can be found. As the participation of MIII-valence electrons increases near the valence band, the Egap value gradually decreases. The degree of participation of MIII-valence electrons can also be explained by the binding ability of Se towards MIII-valence electrons (Fig. 5b–d). Considering that the electronegativity of In is weaker than that of Ga, the factor that affects the Egap value is likely to come from the bond length.The PDOS analysis reveals that the primary distinction between Cs2SnAs2 and Rb2SnAs2 lies in the Sn–As bond (Fig. 6a and b). The electron localization in the Sn–As bond of Cs2SnAs2 is marginally greater than that in the Sn–As bond of Rb2SnAs2. The disparity in Egap values may primarily stem from the spatial separation between 1D-[SnAs2]∞ chains. The degree of electronic localization of the Sn–As bond is significantly greater in K2SnAs2 compared to Cs2SnAs2 and Rb2SnAs2. The average Sn–As bond lengths of these three 1D-[SnAs2]∞ structures are 2.68 Å, 2.67 Å, and 2.62 Å, respectively. In these 1D structures, their bond lengths do not change in the order of Egap values, so the correlation between Egap values and bond lengths may not be significant.
Due to the fact that K2BaSn2As4 and K2SnAs2 demonstrate an equivalent level of electronic localization, their Egap values are comparable (Fig. 6c and d). To acquire more practical Egap values, the HSE06 functional was employed to recalculate the Egap values of both K2BaSn2As4 and K2SnAs2. The subsequent values of 1.77 eV and 1.49 eV for the calculated calibration band gaps may indicate that internal distortion positively influences the expansion of the Egap value of the 1D-[SnAs2]∞ chains. Particularly, the degree of Zn involvement near EF distinguishes BaZnSiSe4 from SrZnSiSe4 with regard to the Zn–Se bond (Fig. 6e and f). In terms of bond length, the average Zn–Se bond lengths of these two structures are 2.48 Å and 2.53 Å, respectively, while their Si–Se average bond lengths are 2.28 Å and 2.32 Å, respectively. It can be seen that the compactness of 1D chains in BaZnSiSe4 is significantly higher than that in SrZnSiSe4.
Achieving a narrower Egap value may be the consequence of decreasing the distance between 1D-[SnAs2]∞ without introducing internal distortion. Furthermore, a reduction in electronegativity between Ge and Se could potentially result in the development of narrow Egap values. But in AI–AII–MIII–Se, bond length also affects the bound state of the electron gas. This may indicate that the pattern of Egap values varies when the type of anion changes. A slight increase in complexity may ensue when distortion is present within the 1D-[MX2]∞ chains. Internal distortion stretching substantially elongates the bond length of Sn–As in 1D-[SnAs2]∞ chains, an effect that substantially amplifies the Egap values. However, for 1D-[ZnSiSe4]∞ chains, Egap values will be weakened as the bond length increases.
PDOS offers a lucid analysis of the contribution of each atomic orbital to each band, elucidating the optical characteristics of crystals primarily originating from various electronic transitions within the band spectrum. Therefore, by using PDOS, not only can we delve deeper into material Egap, but we can also discern the contribution rates of individual functional groups to optical properties.
5 Optical properties
5.1 Linear optical properties
A systematic calculation of the linear optical properties of these eight structures was performed under the assumption of stable and convergent wavefunction conditions. The correlation between structure and linear optics is readily apparent, as the chemical environment of 1D-[ZnGeSe4]∞ is essentially uniform along both the a- and b-axes (Fig. 7a). Phase matching occurs at a distance of approximately 520 nm to 1040 nm in BaZnGeSe4, and the disparity in refractive indices between the nx and ny directions can be minimal. Even under the same valence conditions, a change in atomic type can significantly alter the linear optical properties of the crystal. In the AI–AII–MIII–Se system, the positions where these three materials generate phase matching are very close, but their Δn increases sequentially (Fig. 7b–d). This may be due to the larger atomic radius of the In atom, leading to an increased degree of charge shift.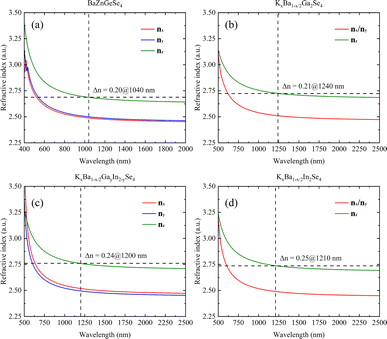 | ||
| Fig. 7 (a)–(d) The linear optical properties of BaZnGeSe4, KxBa1−x/2Ga2Se4, KxBa1−x/2GayIn2−ySe4, and KxBa1−x/2In2Se4. | ||
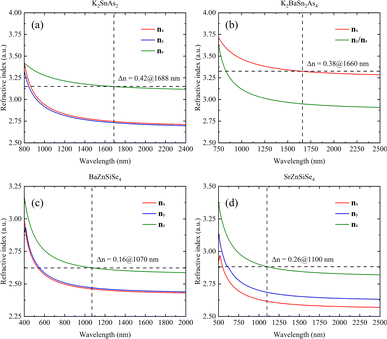
The calculation results also indicate that K2SnAs2 has excellent birefringence and can achieve phase matching of Δn = 0.42 at 1688 nm. In contrast, the Δn of K2BaSn2As4 at 1660 nm is about 0.38, which is slightly lower than the Δn of K2SnAs2 (Fig. 8a and b). The overall refractive index of K2BaSn2As4 on the three axes is higher than K2SnAs2, and their cut-off bands are positively correlated with the Egap value. However, due to the generally low Egap value of arsenides, their absorption cut-off band is larger than that of selenides.
The refractive index of BaZnSiSe4 is significantly lower than that of 1D-[SnAs2]∞ chains. BaZnSiSe4 can achieve phase matching at 1070 nm, and its Δn is approximately 0.16. Although I-[ZnSiSe4]∞ chains and I-[SnAs2]∞ chains have similar configurations, there is a significant difference in their refractive indices (Fig. 8c). The influence of atomic type on refractive index is worth considering, especially for heavier atoms. SrZnSiSe4 can achieve phase matching at 1100 nm, and the Δn between nz and nx reaches 0.26 (Fig. 8d). Considering the situation in 1D-[SnAs2]∞ chains, the impact of internal distortion on the Δn of 1D-[MX2]∞ crystals is different. To explain this phenomenon, a more detailed analysis of these 1D chains is needed.
5.2 Nonlinear optical properties
Systematically calculating the NLO properties of these structures is in addition to their linear optics properties. BaZnGeSe4 has a deff of approximately 28.03 pm V−1 (2050 nm), and its predominant second-order polarization is in the xxz direction (Fig. 9a). Particularly in the case of M disorder, the substitution of elements with the same valence state has a significantly greater effect on second-order polarization than on first-order polarization. In AI–AII–MIII–Se, KxBa1−x/2GayIn2−ySe4 has the maximum deff, and its second-order polarization is mainly concentrated in the d33 direction (Fig. 9b–d). The relative difference between KxBa1−x/2Ga2Se4 and KxBa1−x/2In2Se4 is also worth noting, and the calculation results show that the former's deff is much greater than the latter's deff. Whether this difference exists due to the Egap value or the polarity of the 1D-[MSe2]∞ chains themselves is unknown. Further elucidation of the aforementioned calculation outcomes requires a theoretical analysis on a more microscopic scale.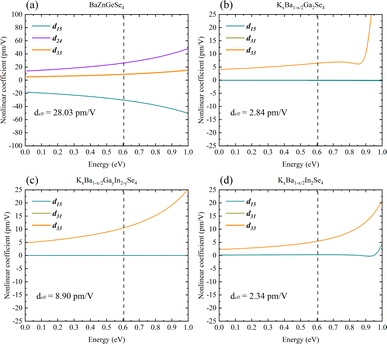 | ||
| Fig. 9 (a)–(d) The nonlinear optical properties of BaZnGeSe4, KxBa1−x/2Ga2Se4, KxBa1−x/2GayIn2−ySe4, and KxBa1−x/2In2Se4. | ||
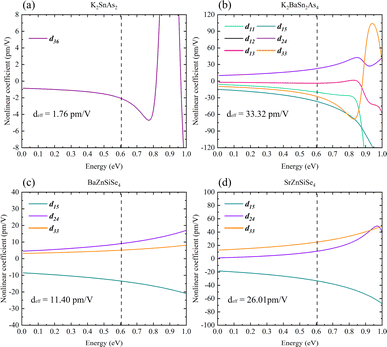
It has been possible to predict the NLO properties of K2SnAs2 for the first time, with a deff of approximately 1.76 pm V−1 (2050 nm). The primary cause of the low NLO in K2SnAs2 at the macroscopic level is the dearth of non-centrosymmetric components within the cell (Fig. 10a). Aside from the 1D-[SnAs2]∞ chains situated at the geometric center, which possesses non-centrosymmetric characteristics, the remaining components are centrosymmetric. In contrast to the intricate configuration of 1D-[SnAs2]∞ chains in K2SnAs2, the theoretical framework is considerably more straightforward. K2BaSn2As4 has a deff of up to 33.32 pm V−1 (2050 nm) as a result of its non-centrosymmetric structure and strong consistent arrangement (Fig. 10b). Undoubtedly, significant distortion occurs not only in the relative positions of Sn4+ ions but also among As3− ions. The anion theory posits that the predominant cause of nonlinear properties are these As3− ions.73
BaZnSiSe4 and SrZnSiSe4 have the deff values 11.40 pm V−1 (2050 nm) and 26.01 pm V−1 (2050 nm), respectively (Fig. 10c and d). The close proximity between the calculated and experimental outcomes demonstrates that the parameter settings for the calculations are logical and convergent. Consequently, internal distortion improves the overall NLO characteristics of the crystal. Nonetheless, in light of the substantial disparity between the Egap values of BaZnSiSe4 and SrZnSiSe4, additional investigation into the deep microscopic mechanism of 1D-[MX2]∞ chains is required (Table 3).
| Crystal | This work | Experiment | |||||
|---|---|---|---|---|---|---|---|
| Egap (eV) | Δn | deff (pm V−1) | Eopt (eV) | Δn | SHG | Ref. | |
| BaZnGeSe4 | 1.52 | 0.20 | 28.03 | 2.46 | — | <2.0 × AGS | 35 |
| KxBa1−x/2Ga2Se4 | 1.71 | 0.21 | 2.84 | 2.03 | — | <0.9 × AGS | 40 |
| KxBa1−x/2GayIn2−ySe4 | 1.61 | 0.24 | 8.90 | 2.34 | — | <0.5 × AGS | 37 |
| KxBa1−x/2In2Se4 | 1.54 | 0.25 | 2.34 | 2.60 | — | <0.5 × AGS | 37 |
| K2SnAs2 | 0.81 (1.49) | 0.42 | 1.76 | — | — | — | 55 |
| K2BaSn2As4 | 0.80 (1.77) | 0.38 | 33.32 | — | — | — | — |
| BaZnSiSe4 | 2.32 | 0.16 | 11.40 | 2.71 | — | <0.6 × AGS | 35 |
| SrZnSiSe4 | 2.00 | 0.26 | 26.01 | 1.95 | — | <2.0 × AGS | 36 |
5.3 Inherent properties of 1D-[MX2]∞ chains
From a molecular standpoint, it is efficient to investigate the inherent characteristics of comparable 1D structures (characterized by identical elemental valence and configuration).74 The process commenced with the methodical calculation of the frontier molecular orbitals of the M2X6 molecules (Fig. 11). In accordance with the band structure, the Egap values of molecules Ga2Se6, GaInSe6, and In2Se6 diminish in a sequential fashion. This result suggests that the variation in Egap values is attributable to 1D-[MX2]∞ chains as opposed to alkaline ions. Nevertheless, both calculation methods were unable to faithfully replicate the pattern of Eopt values; the same issue persists even in the reported calculation results. Moreover, the Egap value of ZnGeSe6 is considerably greater than that of Ga2Se6, and this result of the calculation is more in line with the Eopt values.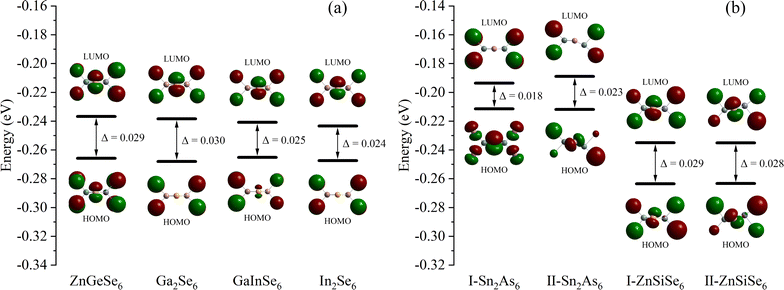 | ||
| Fig. 11 (a) and (b) The Egap (HOMO–LUMO) of ZnGeSe6, Ga2Se6, GaInSe6, In2Se6, I-Sn2As6, II-Sn2As6, I-ZnSiSe6, and II-ZnSiSe6. | ||
In Sn2As6, II-Sn2As6 has a wider Egap value than I-Sn2As6. This corresponds to the calculated EHSE06 values, demonstrating the effect of internal distortion on expanding the Egap values of 1D-[SnAs2]∞ chains. The calculation results also indicate that the Egap value of II-ZnSiSe6 is slightly lower than that of I-ZnSiSe6. The energy difference between HOMO and LUMO is widened as a result of the contraction of bond length in ZnSiSe6, this minute difference is greatly magnified in the crystal field. The band structure is consistent with the calculation results of ZnSiSe6, suggesting that the majority of the variation in Egap values originates from 1D-[ZnSiSe4]∞ chains. The difference in Egap values between I-ZnSiSe6 and ZnGeSe6 can be almost negligible, but their Egap values are both higher than those of II-ZnSiSe6.
In terms of optical properties, by using Δα, it is possible to directly determine the polarity of similar molecules numerically (Fig. 12a). Corresponding to the refractive index, the Δα values of the three molecules Ga2Se6, GaInSe6, and In2Se6 increase sequentially. The Δα of ZnGeSe6, I-ZnSiSe6, and II-ZnSiSe6 molecules also corresponds to their Δn (Fig. 12b). I-Sn2As6 has a visible central symmetry characteristic, resulting in a Δα of up to 61.17 × 10−24 esu. Benefit by the significant difference in position between Sn4+, the central symmetry of II-Sn2As6 is much weaker. This structural change results in II-Sn2As6's Δα (56.29 × 10−24 esu) being weaker than I- Sn2As6's Δα.
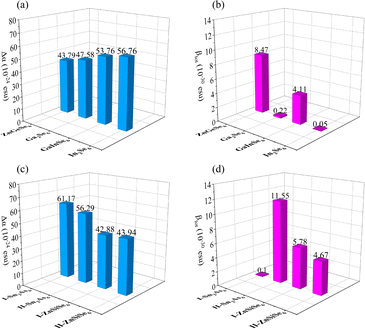 | ||
| Fig. 12 (a)–(d) The Δα and βtot of ZnGeSe6, Ga2Se6, GaInSe6, In2Se6, I-Sn2As6, II-Sn2As6, I-ZnSiSe6, and II-ZnSiSe6. | ||
Although visually, II-ZnSiSe6 has a more exaggerated degree of distortion than I-ZnSiSe6. But in fact, in terms of the degree of central symmetry, II-ZnSiSe6 is actually better than I-ZnSiSe6. The Δα values for II-ZnSiSe6 and I-ZnSiSe6 are 43.94 × 10−24 esu and 42.88 × 10−24 esu, respectively. In the direction of these 1D chains, the length of II-ZnSiSe6 should be greater than the length of I-ZnSiSe6. In addition, the Δα of ZnGeSe6 is also slightly smaller than that of I-ZnSiSe6. These results all explain the underlying reason why SrZnSiSe4 has a higher refractive index than BaZnSiSe4, including ZnGeSe6's weak linear optical ability.
Additionally, the second-order optical properties of analogous molecules can be elucidated using βtot.75 It appears that M2X6 molecules of identical elemental composition exhibit a delicate equilibrium between the dipole hyperpolarizability and the first dipole hyperpolarizability (Fig. 12c). It is noteworthy to mention that the βtot of the dual element system is considerably lower than that of the multi-element system in M2Se6. The βtot of GaInSe6 is several tens of times higher than the other two M2Se6 (Ge2Se6 and In2Se6), although their molecular configurations are almost identical. But in terms of microstructure, the bond length of Ga–Se is smaller than that of In–Se. This causes the GaInSe6 molecules to tilt to one side and produce good second-order polarization ability.
I-Sn2As6 has almost no second-order optical properties, while II-Sn2As6's βtot reaches an astonishing 11.55 × 10−30 esu (Fig. 12d). The same phenomenon also occurs in ZnSiSe6, where I-ZnSiSe6 has a higher βtot than II-ZnSiSe6. Although the difference in Egap values between ZnGeSe6 and I-ZnSiSe6 is not significant, the former's βtot is twice that of the latter. This also indicates the importance of highly electronegative M elements for second-order polarization. Pn materials' exceptional NLO capability is, in fact, largely attributable to the electronegativity difference between M and Pn. As the binding ability of Pn ions to valence electrons (M) decreases, the material's Egap value correspondingly decreases. This can also facilitate the influence of external electric fields on electrons within the crystal field. Sn2As6 has a greater potential than M2Se6 with regard to second-order optical properties.
However, a contradiction exists here. BaZnSiSe4 should possess a greater NLO capability than SrZnSiSe4, according to the results of the βtot. In reality, SrZnSiSe4 possesses an NLO ability that is far superior to BaZnSiSe4's. Without taking into account the scissor, the deff of BaZnSiSe4 remains below 19.96 pm V−1 (2050 nm). From the perspective of crystal field, the interaction between 1D chains is also a significant factor that cannot be ignored. In order to restore the environment of the crystal field, the βtot values of [I-ZnSiSe6] × 4 and [II-ZnSiSe6] × 4 are additionally calculated. The pleasant surprise is the calculation results indicate that βtot (31.96 × 10−30 esu) in [II-ZnSiSe6] × 4 far exceeds βtot (1.19 × 10−30 esu) in [I-ZnSiSe6] × 4. The principal reflection of the component difference between the two is in the zzz direction, where the calculated data for the nonlinear coefficients are located. The aforementioned calculation outcomes methodically elucidate the intrinsic factors that contribute to the simultaneous existence of excellent Δn and outstanding deff in SrZnSiSe4. This suggests that the configuration of 1D-[MX2]∞ chains significantly affects NLO, in addition to the second-order polarization capability of the functional groups themselves.
The contributions of orbitals in PDOS indicate that [ZnSe4] group predominantly governs the optical properties near EF, while [SiSe4] and [GeSe4] groups primarily control the optical properties of the intermediate bands. Additionally, the subtle optical properties at the lower levels are predominantly modulated by AI/AII ions. From the perspective of occupancy, [SiSe4] and [GeSe4] groups contribute significantly to the overall optical properties of the crystal and are the primary sites of charge transfer. Therefore, in regulating NLO capabilities, emphasis should be placed on the properties of high charge density groups and their arrangement.
6 Conclusions
To advance the NLO capability of 1D-[MX2]∞ structures, this work suggests a number of efficient structural strategies. A decrease in the electronegativity difference (M–X) can, in general, cause the nonlinear coefficient to increase considerably. It is worth noting, nevertheless, that a low Egap value can readily result in an excessively broad absorption cut-off band. A slight reduction in birefringence capability may occur as a result of the non-centrosymmetric distortion occurring within the 1D-[MX2]∞ chains, which can substantially increase the material's nonlinear coefficient. Furthermore, it is noteworthy to consider the second-order polarization superposition effect that occurs between 1D-[MX2]∞ chains. Finally, it is advantageous to incorporate [MPn4] into 1D-[MX2]∞ chains (while introducing internal distortions), particularly when the arrangement exhibits a strong tetrahedral consistency. In summary, this theoretical investigation not only conducts a comprehensive examination of the optical properties and electronic configuration of 1D-[MX2]∞ structures, but also offers structurally sound recommendations for the forthcoming fabrication of MIR-NLO optical crystals with exceptional performance.Author contributions
Chaoyi Zhu: writing – original draft, conceptualization, data curation, methodology.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The author gratefully acknowledges financial support from the Shanghai Institute of Measurement and Testing Technology.References
- A. Nataraj, B. Tuzson, M. Gianella, I. Prokhorov, G. Li, V. Ebert, J. Faist and L. Emmenegger, Anal. Chem., 2023, 95, 5354–5361 CrossRef CAS PubMed.
- L. Yu, J. Liang, Q. Zeng, J. Wang, X. Luo, J. Wang, P. Yan, F. Dong, X. Liu and Q. Lü, High Power Laser Sci. Eng., 2023, 11, e53 CrossRef CAS.
- L. M. Narlagiri, M. Bharati, R. Beeram, D. Banerjee and V. R. Soma, TrAC, Trends Anal. Chem., 2022, 153, 116645 CrossRef CAS.
- W. Harmon, K. Robben and C. M. Cheatum, Opt. Lett., 2023, 48, 4797–4800 CrossRef CAS PubMed.
- W. Zhou, J. Wu, W. Liu and S. P. Guo, Coord. Chem. Rev., 2023, 477, 214950 CrossRef CAS.
- F. Wang, Y. Chen, C. Li, T. Ma, X. Wang, K. Yu and L. Li, Opt. Commun., 2022, 502, 127418 CrossRef CAS.
- R. Zhao, S. Wu, X. Lei, H. Liu, Z. Wang, Y. Yu and G. Jin, Opt. Laser Technol., 2024, 170, 110230 CrossRef CAS.
- H. Huo, Z. Lin and L. Kang, Mater. Today Phys., 2022, 28, 100894 CrossRef CAS.
- C. Jin, X. Jiang, C. Wu, K. Duanmu, Z. Lin, Z. Huang, M. G. Humphrey and C. Zhang, Angew. Chem., Int. Ed., 2023, 135, e202310835 CrossRef.
- L. Luo, L. Wang, J. Chen, J. Zhou, Z. Yang, S. Pan and J. Li, J. Am. Chem. Soc., 2022, 144, 21916–21925 CrossRef CAS PubMed.
- D. Mei, W. Cao, N. Wang, X. Jiang, J. Zhao, W. Wang, J. Dang, S. Zhang, Y. Wu and P. Rao, Mater. Horiz., 2021, 8, 2330–2334 RSC.
- J. Peng, X. Liu, J. Wang, S. Zhang, X. Xiao, Z. Xiong, K. Zhang, B. Chen, Z. He and W. Huang, Inorg. Chem., 2023, 62, 12067–12078 CrossRef CAS PubMed.
- C. Li, Z. Li, M. Sun, C. Huang and J. Yao, J. Cryst. Growth, 2022, 577, 126405 CrossRef CAS.
- Y. Wang, J. Liu, C. Cui, F. Liang, D. Lu, J. Wang, J. Ma, H. Zhang, G. Xie and H. Yu, Opt. Mater. Express, 2022, 12, 863–875 CrossRef CAS.
- V. Bhat, C. P. Callaway and C. Risko, Chem. Rev., 2023, 123, 7498–7547 CrossRef CAS PubMed.
- B. Zhang, X. Zhang, J. Yu, Y. Wang, K. Wu and M. H. Lee, Chem. Mater., 2020, 32, 6772–6779 CrossRef CAS.
- M. Wu, E. Tikhonov, A. Tudi, I. Kruglov, X. Hou, C. Xie, S. Pan and Z. Yang, Adv. Mater., 2023, 35, 2300848 CrossRef CAS PubMed.
- C. L. Hu, Y. X. Han, Z. Fang and J. G. Mao, Chem. Mater., 2023, 35, 2647–2654 CrossRef CAS.
- Y. Yun, M. Wu, C. Xie, Z. Yang, G. Li and S. Pan, Adv. Opt. Mater., 2023, 11, 2300256 CrossRef CAS.
- W. Cai, A. Abudurusuli, C. Xie, E. Tikhonov, J. Li, S. Pan and Z. Yang, Adv. Funct. Mater., 2022, 32, 2200231 CrossRef CAS.
- P. Wang, Y. Chu, A. Tudi, C. Xie, Z. Yang, S. Pan and J. Li, Adv. Sci., 2022, 9, 2106120 CrossRef CAS PubMed.
- F. Castet, C. Tonnelé, L. Muccioli and B. Champagne, Acc. Chem. Res., 2022, 55, 3716–3726 CrossRef CAS PubMed.
- A. Tudi, C. Xie, S. Pan and Z. Yang, Mater. Today Phys., 2022, 28, 100852 CrossRef CAS.
- P. F. Li, C. L. Hu, J. G. Mao and F. Kong, Mater. Horiz., 2024, 11, 1704–1709 RSC.
- Z. Qian, H. Wu, Z. Hu, J. Wang, Y. Wu and H. Yu, Angew. Chem., Int. Ed., 2024, 63, e202400892 CrossRef CAS PubMed.
- B. Zerulla, D. Beutel, C. Holzer, I. F. Corbaton, C. Rockstuhl and M. Krstić, Adv. Mater., 2024, 36, 2311405 CrossRef CAS PubMed.
- C. Che, R. Xue, N. Li, P. Gupta, X. Wang, B. Zhao, S. Singamaneni, S. Nie and B. T. Cunningham, ACS Nano, 2022, 16, 2345–2354 CrossRef CAS PubMed.
- P. V. Pham, S. C. Bodepudi, K. Shehzad, Y. Liu, Y. Xu, B. Yu and X. Duan, Chem. Rev., 2022, 122, 6514–6613 CrossRef CAS PubMed.
- Y. Xiong, S. Shepherd, J. Tibbs, A. Bacon, W. Liu, L. D. Akin, T. Ayupova, S. Bhaskar and B. T. Cunningham, Micromachines, 2023, 14, 668 CrossRef PubMed.
- H. Wang, Y. Chu, X. Pan, Z. Yang, S. Pan and J. Li, Mater. Today Phys., 2023, 38, 101243 CrossRef CAS.
- H. D. Yang, M. Y. Ran, S. H. Zhou, X. T. Wu, H. Lin and Q. L. Zhu, Chem. Sci., 2022, 13, 10725–10733 RSC.
- Q. Q. Liu, X. Liu, L. M. Wu and L. Chen, Angew. Chem., Int. Ed., 2022, 134, e202205587 CrossRef.
- Y. Guo, F. Liang, W. Yin, Z. Li, X. Luo, Z. S. Lin, J. Yao, A. Mar and Y. Wu, Chem. Mater., 2019, 31, 3034–3040 CrossRef CAS.
- Y. Guo, F. Liang, Z. Li, W. Xing, Z. S. Lin, J. Yao, A. Mar and Y. Wu, Inorg. Chem., 2019, 58, 10390–10398 CrossRef CAS PubMed.
- W. Yin, A. K. Iyer, C. Li, J. Yao and A. Mar, J. Alloys Compd., 2017, 708, 414–421 CrossRef CAS.
- M. Ma, J. Dang, Y. Wu, X. Jiang and D. Mei, Inorg. Chem., 2023, 62, 6549–6553 CrossRef CAS PubMed.
- Z. X. Chen, Y. N. Li, W. D. Yao, W. Liu and S. P. Guo, J. Alloys Compd., 2022, 899, 163255 CrossRef CAS.
- J. X. Zhang, P. Feng, M. Y. Ran, X. T. Wu, H. Lin and Q. L. Zhu, Coord. Chem. Rev., 2024, 502, 215617 CrossRef CAS.
- W. Wang, D. Mei, F. Liang, J. Zhao, Y. Wu and Z. Lin, Coord. Chem. Rev., 2020, 421, 213444 CrossRef CAS.
- Y. N. Li, Y. Chi, Z. D. Sun, H. Xue, N. T. Suen and S. P. Guo, Chem. Commun., 2019, 55, 13701–13704 RSC.
- M. R. Majewski, R. I. Woodward and S. D. Jackson, Laser Photonics Rev., 2020, 14, 1900195 CrossRef CAS.
- H. Yoshida, H. Fujita, M. Nakatsuka, M. Yoshimura, T. Sasaki, T. Kamimura and K. Yoshida, Jpn. J. Appl. Phys., 2006, 45, 766 CrossRef CAS.
- J. Ma, Z. Qin, G. Xie, L. Qian and D. Tang, Appl. Phys. Rev., 2019, 6, 021317 Search PubMed.
- H. D. Yang, M. Y. Ran, W. B. Wei, X. T. Wu, H. Lin and Q. L. Zhu, Chem.–Asian J., 2021, 16, 3299–3310 CrossRef CAS PubMed.
- P. G. Schunemann and T. M. Pollak, MRS Bull., 1998, 23, 23–27 CrossRef CAS.
- V. R. Badarla, S. C. Kumar, A. E. Martin, K. Devi, K. T. Zawilski, P. Schunemann and M. E. Zadeh, Opt. Lett., 2016, 41, 1708–1711 CrossRef PubMed.
- J. Chen, H. Chen, F. Xu, L. Cao, X. Jiang, S. Yang, Y. Sun, X. Zhao, C. Lin and N. Ye, J. Am. Chem. Soc., 2021, 143, 10309–10316 CrossRef CAS PubMed.
- T. Yu, S. Wang, X. Zhang, C. Li, J. Qiao, N. Jia, B. Han, S. Q. Xia and X. Tao, Chem. Mater., 2019, 31, 2010–2018 CrossRef CAS.
- J. Chen, C. Lin, G. Peng, F. Xu, M. Luo, S. Yang, S. Shi, Y. Sun, T. Yan and B. Li, Chem. Mater., 2019, 31, 10170–10177 CrossRef CAS.
- J. Mark, J. Wang, K. Wu, J. G. Lo, S. Lee and K. Kovnir, J. Am. Chem. Soc., 2019, 141, 11976–11983 CrossRef CAS PubMed.
- B. Eisenmann and M. Somer, Z. Naturforsch., B: J. Chem. Sci., 1984, 39, 736–738 CrossRef.
- A. Haffner, A. K. Hatz, C. Hoch, B. V. Lotsch and D. Johrendt, Eur. J. Inorg. Chem., 2020, 2020, 617–621 CrossRef CAS.
- J. Chen, Q. Wu, H. Tian, X. Jiang, F. Xu, X. Zhao, Z. Lin, M. Luo and N. Ye, Adv. Sci., 2022, 9, 2105787 CrossRef CAS PubMed.
- B. Eisenmann and J. Klein, J. Less-Common Met., 1991, 175, 109–117 CrossRef CAS.
- S. Burtzlaff, M. Hołyńska and S. Dehnen, Z. Anorg. Allg. Chem., 2010, 636, 1691–1693 CrossRef CAS.
- A. M. Lyapunov, Int. J. Control, 1992, 55, 531–534 CrossRef.
- X. Gonze, F. Jollet, F. A. Araujo, D. Adams, B. Amadon, T. Applencourt, C. Audouze, J. M. Beuken, J. Bieder and A. Bokhanchuk, Comput. Phys. Commun., 2016, 205, 106–131 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- B. Hammer, L. B. Hansen and J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413 CrossRef.
- W. Setyawan and S. Curtarolo, Comput. Mater. Sci., 2010, 49, 299–312 CrossRef.
- G. Goldberg, A. Black, S. Jebb, T. Cole, P. Murgatroyd, W. Coward and A. Prentice, Eur. J. Clin. Nutr., 1991, 45, 569–581 CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- S. Sharma and C. A. Draxl, Phys. Scr., 2004, 2004, 128 CrossRef.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- E. Bitzek, P. Koskinen, F. Gähler, M. Moseler and P. Gumbsch, Phys. Rev. Lett., 2006, 97, 170201 CrossRef PubMed.
- J. D. Head and M. C. Zerner, Chem. Phys. Lett., 1985, 122, 264–270 CrossRef CAS.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283 CrossRef CAS.
- S. Kurtz and T. Perry, J. Appl. Phys., 1968, 39, 3798–3813 CrossRef CAS.
- M. Shkir, S. AlFaify, M. A. Khan, S. Muhammad and A. R. Chaudhry, Optik., 2016, 127, 2852–2860 CrossRef CAS.
- B. Zhang, Z. Yang, Y. Yang, M. H. Lee, S. Pan, Q. Jing and X. Su, J. Mater. Chem. C, 2014, 2, 4133–4141 RSC.
- J. Lin, M. H. Lee, Z. P. Liu, C. Chen and C. J. Pickard, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 13380 CrossRef CAS.
- Y. Qian, Q. Jing, H. Duan, M. H. Lee and H. Cao, Physica B, 2022, 630, 413676 CrossRef CAS.
- X. Shi, Q. Jing, M. H. Lee, H. Cao and M. Long, Chem. Phys. Lett., 2022, 786, 139188 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |