Data-driven exploration of layered double hydroxide crystals exhibiting high fluoride ion adsorption properties and chemical stability†
Fumitaka
Hayashi
 *a,
Ryuki
Harada
a,
Hiroaki
Sugitani
a,
Hiromasa
Kaneko
*a,
Ryuki
Harada
a,
Hiroaki
Sugitani
a,
Hiromasa
Kaneko
 b,
Tien Quang
Nguyen
b,
Tien Quang
Nguyen
 c,
Mongkol
Tipplook
c,
Mongkol
Tipplook
 cd,
Tetsuya
Yamada
cd,
Tetsuya
Yamada
 ad,
Michihisa
Koyama
ad,
Michihisa
Koyama
 cd and
Katsuya
Teshima
cd and
Katsuya
Teshima
 *acd
*acd
aDepartment of Materials Chemistry, Faculty of Engineering, Shinshu University, 4-17-1 Wakasato, Nagano 380-8553, Japan. E-mail: fhaysh@shinshu-u.ac.jp; teshima@shinshu-u.ac.jp
bDepartment of Applied Chemistry, School of Science and Technology, Meiji University, 1-1-1 Higashi-Mita, Tama-ku, Kawasaki-shi, Kanagawa-ken 214-8571, Japan
cInstitute for Aqua Regeneration, Shinshu University, 4-17-1 Wakasato, Nagano 380-8553, Japan
dResearch Initiative for Supra-Materials (RISM), Shinshu University, 4-17-1 Wakasato, Nagano 380-8553, Japan
First published on 10th April 2025
Abstract
Fluoride ion (F−) contamination of groundwater has become a global issue. As potential adsorbents for F− removal, layered double hydroxides (LDHs) have moderate affinities for F−. Moreover, the preparation of LDHs exhibiting both high F− adsorption capacities and chemical stability is empirically challenging. To overcome this issue, we used process informatics to explore promising ternary LDHs with high F− adsorption capacities and chemical stability. We constructed machine learning models based on F− adsorption test data and Bayesian optimisation. Initially, the objective variable for LDH candidates was the F− adsorption amount. By considering LDH systems that combine one type of divalent cation (M2+) with two types of trivalent cation (M3+), ternary LDHs such as Ni–Fe–Ga and Ni–Al–Ga LDHs, which have not been studied previously, were proposed. The subsequent addition of the M2+ leaching amount as an objective variable allowed the identification of LDHs such as Ni–Fe–Y and Ni–Cr–Y LDHs with high F− adsorption capacities (15–17 mg g−1 at 1 mM F−, Kd > 4600–8300 mL g−1) and chemical stability. Projected crystal orbital Hamilton population analysis indicated that the M2+–O bonds in Ni–Al–Ga and Ni–Cr–Y LDHs have a stronger covalent character than those in Mg-based LDHs. These findings provide guidelines for the synthesis of novel LDHs with various compositions.
1. Introduction
The increasing prevalence of fluoride ion (F−) contamination in groundwater necessitates the development of efficient F− removal methods. The World Health Organization has set a maximum limit of 1.5 mg L−1 for F−,1 but many regions of Africa and countries such as China, Canada, Australia, and India are affected by high F− levels. F− naturally occurring in minerals such as calcium fluoride and as a component of volcanic gases can lead to F− dissolution in groundwater.2 Groundwater is also susceptible to contamination by other chemical substances, which can pose threats not only to human and livestock health but also to agriculture.3Various types of materials, including activated alumina, mixed metal oxides or hydroxides, metal–organic frameworks, and carbon-based composites, have been investigated as adsorbents for F− removal from aqueous solution.4–14 In particular, layered double hydroxides (LDHs) are good candidates for F− removal because of their high chemical stability.15–18 As inorganic layered compounds, LDHs are characterised by a structure in which host layers of metal hydroxides alternate with intercalated guests (anions or water molecules). The intercalation of anions or water molecules compensates for the positive charge of the metal hydroxide layers. LDHs have a general formula of [M2+1−xM3+x(OH)2][An−]x/n·yH2O (M2+ = Mg2+, Zn2+, Ni2+, Co2+; M3+ = Al3+, Ga3+, Fe3+; An− = CO32−, SO42−, Cl−; x = 0.2–0.4), where [M2+1−xM3+x(OH)2] represents the positively charged brucite-like sheets and An− represents the intercalated anions.19 Unlike most ion-exchangeable layered materials that undergo cation exchange, LDHs are unique inorganic compounds capable of exchanging anions in the guest layer with those in solution.19,20 The anion selectivity and affinity are dependent on the combination and clustering of structures in the LDH.21 We have previously highlighted the importance of atomic arrangement in two-dimensional hydroxide layers.21,22 The chemical stability of LDHs is also an important issue for practical applications.
Materials informatics, including process informatics, is a powerful methodology for exploring new functional materials.23,24 Machine learning (ML)-based models can be constructed to predict promising candidate variables X based on objective variables Y. Conventional experimental approaches using ML typically select candidates for subsequent experimental conditions based on estimated Y values that are close to the target value. However, if candidates with a higher probability of success are identified, fewer experimental iterations are required to reach the target Y values.
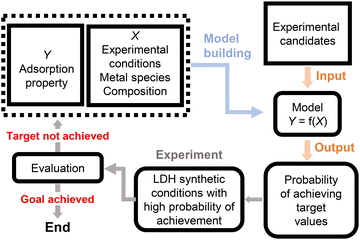
Herein, we introduce an ML-based model for exploring new LDHs that exhibit high F− adsorption capacities and chemical stability. Fig. 1 shows the workflow employed to search for new LDHs using Bayesian optimisation (BO), wherein BO is an ML approach that proposes promising candidate variables X based on Gaussian process regression (GPR).25 First, to search for experimental conditions for synthesising LDH candidates with high F− adsorption capacities, an existing dataset was used to construct a GPR model between features X (experimental conditions and LDH information) and objective variables Y (F− adsorption and M2+ leaching amounts). One million candidate experimental conditions were randomly generated based on the conditions in Table S1 in the ESI† and then input into the constructed GPR model to predict Y values and their variance. An acquisition function was calculated from the predictions and variances, and the candidate experimental conditions with the largest acquisition function values were selected. The LDH candidates were then synthesised using the selected experimental conditions, the F− adsorption and M2+ leaching amounts were analysed, and the obtained numerical results were added to the dataset. Repeating this cycle enabled the efficient exploration of ternary LDH systems, including in extrapolated regions. Consequently, we were able to discover promising new LDHs, such as Ni–Al–Ga, Ni–Fe–Y, and Ni–Cr–Y LDHs, which were not previously known.
2. Materials and methodology
2.1. Datasets
LDH samples for the training and validation datasets were synthesised using the coprecipitation method and then subjected to hydrothermal treatment to increase their crystallinity. The library of training and validation datasets is provided in the ESI.† The synthesis conditions for the LDH samples in the validation dataset are summarised in Tables S2–S6 (runs 1–17) in the ESI.†Analytical-grade salts, including Mg(NO3)2·6H2O, Zn(NO3)2·6H2O, Ni(NO3)2·6H2O, Mn(NO3)2·6H2O, Al(NO3)3·9H2O, Fe(NO3)3·9H2O, Cr(NO3)2·9H2O, Ga(NO3)3·nH2O, Y(NO3)3·nH2O, NaOH, Na2CO3, HCl, and NaCl were purchased from Wako Pure Chemical Industries, Ltd. (Japan) and used as received. Typically, Ni, Fe, and Ga nitrates were dissolved in 100 mL of ultrapure water to obtain a 15–100 mM solution (solution A), and NaOH and Na2CO3 were dissolved in 200 mL of ultrapure water to obtain a 100 mM alkaline solution (solution B). Subsequently, solution B was quickly added dropwise to solution A under stirring at a pH of approximately 10. The obtained mixture was aged for 20 h under continuous stirring. The resulting dispersion was transferred to an autoclave and heated at the desired temperature for the required holding time. After cooling, the slurry was filtered and dried at 60 °C overnight. Finally, after immersion in an acidic aqueous solution containing HCl (33.0 mM) and NaCl (4.0 M) overnight to exchange CO32− with Cl− in the interlayers, the sample was dried at 60 °C under atmospheric conditions. The samples were named using the constituent metal species and atomic fraction of M2+ relative to the total amount of metals (M2+ and M3+). Using run 5 in Table S2 in the ESI† as an example, the sample with a chemical composition of [Ni0.67Fe0.23Ga0.10(OH)2]Cl0.33·nH2O was named Ni–Fe–Ga-067 LDH.
2.2. Ion adsorption tests
The F− adsorption performance of the LDH samples was investigated using batch experiments. Solutions were prepared using reagent-grade NaF (Wako Pure Chemical Industries, Ltd., Japan). In a typical experiment, LDH powder was added to a solution in a capped bottle, and the mixture was agitated overnight at 150 rpm using an automatic shaker. After separating the test solution from the LDH crystals using a 0.2 μm syringe filter, ion chromatography (HIS-20A, Shimadzu, Japan) was used to determine the residual F− concentration in the solution and the adsorption amount q (mg g−1) of F− per gram of LDH. The initial F− concentration was 1 mM.The distribution coefficient Kd was used to evaluate the preference for F− and is expressed by eqn (1):
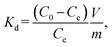 | (1) |
The effect of competitive ions on the Kd was determined using the batch method. The conditions were as follows: F− = 0.2 mM; Cl−, NO3−, HCO3−, SO42− = 0.2 mM; volume/mass ratio = 1000 mL g−1; final pH = 5.6–6.5; room temperature; and shaking time = 1 h. Solutions were prepared using reagent-grade NaF, NaCl, NaNO3, NaHCO3, and Na2SO4 (Wako Pure Chemical Industries, Ltd., Japan). The total anion concentration was 1 mM.
2.3. Characterisation
X-ray diffraction (XRD) patterns were collected using a MiniFlex II diffractometer (Rigaku, Japan) or SmartLab diffractometer (Rigaku, Japan) with monochromated Cu Kα radiation (λ = 0.15418 nm). Field-emission scanning electron microscopy (FE-SEM) images and energy-dispersive X-ray spectroscopy data were obtained using a JSM-7600F instrument (JEOL, Japan). The water content in the samples was determined using thermogravimetry-differential thermal analysis (TG-DTA; Thermo Plus EVOII TG8120, Rigaku, Japan) at a heating rate of 10 °C min−1 in an air flow.2.4. Gaussian process regression (GPR)
GPR is a linear regression analysis method that can be extended to nonlinear regression models using a kernel trick.26 GPR can be used to predict Y values and the variance of the predicted Y values, enabling researchers to discuss the reliability and extrapolation of the predicted Y values. When input x is given, output y(x) is represented as a probability model following a normal distribution. Assuming that the GPR model is linear, the i-th sample is expressed by eqn (2):| y(i) = x(i)b, | (2) |
| mi = E[y(i)] = 0, | (3) |
| σyi,j2 = cov[y(i), y(j)] = x(i)x(j)Tσb2. | (4) |
Input x is transformed by the nonlinear function φ, and σyi,j2 is calculated using eqn (5):
| σyi,j2 = φ(x(i))φ(x(j))Tσb2. | (5) |
| yobs(i) = y(i) + e(i), | (6) |
| σyobsi,j2 = φ(x(i))φ(x(j))Tσb2 + δi,jσe2 = K(x(i), x(j)), | (7) |
In the GPR method, if output yobs = (yobs(1)⋯yobs(n))T corresponding to the past input vector x(1)⋯x(n) is used as training data, the output for the new input vector x(n+1) can be predicted as a normal distribution with mean m(x(n+1)) and variance σ2(x(n+1)) using eqn (8) and (9):
 | (8) |
 | (9) |
| k = [K(x(1), x(n+1)) K(x(i), x(n+1))⋯K(x(n), x(n+1))]. | (10) |
Output  can be predicted as a Gaussian distribution, as shown in eqn (11):
can be predicted as a Gaussian distribution, as shown in eqn (11):
 | (11) |
| K = [K(x(1), x(n))⋯K(x(i), x(n))⋯K(x(n), x(n))], | (12) |
| k* = [K(x(n+1), x(n+1))]. | (13) |
Output yobs(n+1) for the new input vector x(n+1) can be estimated using eqn (14):
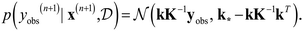 | (14) |
Similar to the dataset, the X variables are the heating temperature [°C], holding time [h], M2+, MI3+ × 1, MI3+ × 2, and F− concentration [mM], as summarised in Table S1 in the ESI.†
2.5. Bayesian optimisation (BO)
BO is a method for calculating an acquisition function (AF) that considers the predicted Y values and the variance of the predicted Y values and for selecting candidate variables X with the highest AF values.27,28 In BO, the GPR model is used to calculate a predicted Y value and its variance for a new sample, which are then used to calculate an AF value. In this study, we used the probability of improvement (PI) and probability in the target range, which can be reasonably extended to multiple Y values as an AF. The PI is the probability that the predicted Y value is higher than the maximum value of the existing samples, which corresponds to the integration of the maximum value of Y (Ymax) in the samples to infinity in a normal distribution, where the estimated Y value and its variance are the mean and variance, respectively. PI(xnew), the PI value in new sample xnew, is given by eqn (15): | (15) |
The probability that the predicted Y value is less than the minimum value of the samples can be expressed by calculating the PI after multiplying the Y values by −1. The probability in the target range, which is the probability that the estimated Y value falls within the target range, is expressed as the difference between the PI determined using the upper limit of the set range (Yrange,max) and that determined using the lower limit of the set range (Yrange,min), as in eqn (16):
| PTR(xnew) = PImin(xnew) − PImax(xnew), | (16) |
 | (17) |
 | (18) |
2.6. Random forest (RF) analysis
The RF regression method is based on ensemble learning. In this method, multiple decision trees are constructed, and the predictions are integrated to obtain a final prediction.29 Samples and X variables are randomly selected from the dataset, and decision trees are constructed. The predictive performance of the RF models can be evaluated using out-of-bag data, which are samples not used in constructing the decision tree. The importance of the X variables can be evaluated using eqn (19):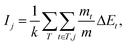 | (19) |
2.7. First-principles calculations
Simulations of the three LDH systems, namely Ni–Al–Ga, Ni–Cr–Y, and Mg–Al LDHs, were performed within the framework of density functional theory (DFT) using the Vienna ab initio simulation Package.30,31 The systems were modeled using a 3 × 3 × 1 supercell containing 171 atoms, where a periodic arrangement of divalent and trivalent cations resulted in a cation ordering pattern. Initially, intercalated chloride (Cl−) ions and water molecules were placed in an orderly manner within the interlayer, with the Cl− ions positioned on top of the trivalent cations. Spin-polarized calculations were carried out using the projector augmented wave method,32,33 and the Perdew–Burke–Ernzerhof functional34 was used for the exchange-correlation treatment. The Brillouin zone was sampled using a 2 × 2 × 1 k-point mesh, and a plane-wave cutoff energy of 520 eV was employed. To account for long-range van der Waals interactions, the Becke–Johnson damping variant of the DFT-D3 dispersion correction was applied.35 The systems were fully optimized until the forces on all atoms were less than 0.02 eV Å−1. Bonding analysis was conducted using the LOBSTER program to determine the crystal orbital Hamilton population (COHP),36–38 which provides insights into the nature and strength of the chemical bonds in the systems.
cation ordering pattern. Initially, intercalated chloride (Cl−) ions and water molecules were placed in an orderly manner within the interlayer, with the Cl− ions positioned on top of the trivalent cations. Spin-polarized calculations were carried out using the projector augmented wave method,32,33 and the Perdew–Burke–Ernzerhof functional34 was used for the exchange-correlation treatment. The Brillouin zone was sampled using a 2 × 2 × 1 k-point mesh, and a plane-wave cutoff energy of 520 eV was employed. To account for long-range van der Waals interactions, the Becke–Johnson damping variant of the DFT-D3 dispersion correction was applied.35 The systems were fully optimized until the forces on all atoms were less than 0.02 eV Å−1. Bonding analysis was conducted using the LOBSTER program to determine the crystal orbital Hamilton population (COHP),36–38 which provides insights into the nature and strength of the chemical bonds in the systems.
3. Results and discussion
In the first cycle, BO was performed using a single objective variable Y (F− adsorption amount). The explanatory variables X, including the types of metals and synthetic conditions, used in the ML model are summarised in Table S1 in the ESI.† Experimental conditions for synthesising LDHs were proposed based on high PI values for the AF, as summarised in Table S2 in the ESI,† and the following five LDH systems were selected: Mn–Cr–Y, Mn–Y, Mg–Y, Mg–Fe–Y, and Ni–Fe–Ga LDHs. Fig. 2 shows the XRD patterns of the obtained LDHs, and we found that Ni–Fe–Ga-067 LDH was obtained as a single-phase LDH crystal after the hydrothermal treatment, whereas the Mn–Cr–Y, Mn–Y, Mg–Y, and Mg–Fe–Y LDH samples did not exhibit any peaks derived from a layered structure.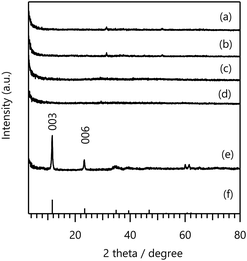 | ||
| Fig. 2 XRD patterns of (a) Mn–Cr–Y-067, (b) Mn–Cr-067, (c) Mg–Y-070, (d) Mg–Fe–Y-080, and (e) Ni–Fe–Ga-067 LDHs with that of (f) Mg0.667Al0.33(OH)2(CO3)0.166·0.5H2O (PDF 00-066-0802) shown for comparison. The synthetic conditions for the LDHs are summarised in Table S2 in the ESI.† | ||
The results of the F− adsorption tests and M2+ leaching analysis are presented in Table S2 in the ESI.† The LDH samples without a layered structure (Mn–Cr–Y, Mn–Y, Mg–Y, and Mg–Fe–Y LDHs) exhibited lower F− adsorption amounts than conventional LDHs. In contrast, Ni–Fe–Ga-067 LDH with a layered structure showed a high F− adsorption amount of 18.6 mg g−1 and a removal rate of 97.7% (Kd = 4248 mL g−1). SEM imaging of Ni–Fe–Ga-067 LDH (Fig. S1 in the ESI†) revealed LDH particles with a lateral size of 200–300 nm. The chemical composition of this sample was analysed using ICP-OES, as summarised in Table S3 in the ESI.† The Ni and Fe contents in Ni–Fe–Ga-067 LDH corresponded well to the target composition, whereas the Ga3+ content deviated by approximately 40%, mainly because of the effect of the hydrate of the Ga source. Based on the TG-DTA profile of Ni–Fe–Ga-067 LDH in Fig. S2 in the ESI,† the water content was estimated to be 4.9 wt%. Thus, the chemical formula of this sample can be written as [Ni0.70Fe0.24Ga0.06(OH)2][Cl−]0.30·0.30H2O.
Using the GPR for a second cycle, BO was conducted to select the next five samples with high PI values for the AF (Table S4 in the ESI†). The selected compositions were Ni–Y, Ni–Fe–Cr, Mg–Al–Ga, Mn–Al–Fe, and Ni–Al–Ga. Among these samples, Ni–Y LDH consisted of two elements, whereas the other four samples were ternary LDHs. Compared with the first cycle, the divalent metal Ni2+ was predominantly chosen in the second cycle. In addition, the second cycle proposed LDHs with various combinations of Al, Fe, and Ga. Similar to the first cycle, all the experimental candidates differed from those in the starting dataset. As shown by the XRD patterns in Fig. 3, Mg–Al–Ga, Ni–Al–Ga, and Ni–Fe–Cr LDHs were synthesised as single-phase LDH structures, whereas Mn–Al–Fe and Ni–Y LDHs did not exhibit peaks characteristic of layered structures.
 | ||
| Fig. 3 XRD patterns of (a) Ni–Y-080, (b) Ni–Fe–Cr-067, (c) Mg–Al–Ga-067, (d) Mn–Al–Fe-067, (e) Ni–Al–Ga-067 LDHs with those of (f) Mg0.667Al0.33(OH)2(CO3)0.166 (PDF 00-066-0802) and (g) Mn3O4 (PDF 00-013-0162) shown for comparison. The synthetic conditions for the LDHs are summarised in Table S4 in the ESI.† | ||
The results of the F− adsorption tests and M2+ leaching analysis are presented in Table S4 in the ESI.† The Ni–Y-080 and Mn–Al–Fe-067 LDH samples without layered structures exhibited lower F− adsorption amounts than the other LDHs. Although Mg–Al–Ga-067 and Ni–Al–Ga-067 LDHs showed high F− adsorption amounts (>17.4 mg g−1), these samples did not outperform Ni–Fe–Ga-067 LDH synthesised in the first cycle. However, Ni–Fe–Ga-067 LDH exhibited a greater extent of M2+ dissolution, indicating that the LDHs synthesised in the second cycle achieved higher chemical stability than those synthesised in the first cycle.
Next, we explored LDHs with both high F− adsorption capacities and chemical stability using two objective variables Y (F− adsorption and M2+ leaching amounts). We selected five samples (Zn–Al–Ga, Zn–Al–Y, Zn–Al–Fe, and Zn–Al–Cr LDHs) with high PI values for the AF using GPR, and the corresponding experimental conditions X are summarised in Table S5 in the ESI.†Fig. 4 on the top panel shows XRD patterns of the obtained LDH crystals. Only Zn–Al–Ga-067 LDH exhibited a single-phase LDH structure. Although LDH-derived peaks were observed for Zn–Al–Ga-080 and Zn–Al–Cr, a ZnO impurity phase was also observed.
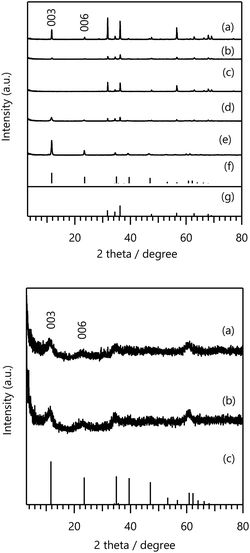 | ||
| Fig. 4 (Top) XRD patterns of (a) Zn–Al–Ga-080, (b) Zn–Al–Y-080, (c) Zn–Al–Fe-080, (d) Zn–Al–Cr-080, and (e) Zn–Al–Ga-067 LDHs with those of (f) Mg0.667Al0.33(OH)2(CO3)0.166·0.5H2O (PDF 00-066-0802) and (g) ZnO (PDF 00-036-1451) shown for comparison. The synthetic conditions for the LDHs are summarised in Table S5 in the ESI.† (Bottom) XRD patterns of (a) Ni–Fe–Y-067 and (b) Ni–Cr–Y-067 with that of (c) Mg0.667Al0.33(OH)2(CO3)0.166·0.5 H2O (PDF 00-066-0802) shown for comparison. The synthetic conditions for the LDHs are summarised in Table S6 in the ESI.† | ||
The results of the F− adsorption tests and M2+ leaching analysis in Table S5 in the ESI† reveal that the Zn–Al–Ga, Zn–Al–Y, Zn–Al–Fe, and Zn–Al–Cr LDH samples with a ZnO impurity phase exhibited lower F− adsorption amounts than the other LDHs. Zn–Al–Ga-067 LDH showed a high adsorption capacity of 18.5 mg·g−1, but the M2+ leaching amount was 5.87 mg·L−1, indicating poor chemical stability.
After incorporating the proposed samples into the dataset, we conducted BO again using the GPR to select two samples with high PI values for the AF. The proposed experimental conditions X of the selected samples (Ni–Fe–Y-067 and Ni–Cr–Y-067 LDHs) are summarised in Table S6 in the ESI.† Similar to the first cycle, only LDHs with three elements were proposed. As shown by the XRD patterns in the bottom panel of Fig. 4, both selected samples were obtained as single-phase LDHs. Furthermore, ICP-OES analysis revealed that the Fe, Cr, and Y ion contents of the Ni–Fe–Y and Ni–Cr–Y LDH samples were similar to the target composition, and the chemical formulas were determined to be [Ni0.64Fe0.25Y0.09(OH)2Cl0.34] and [Ni0.67Cr0.25Y0.08(OH)2Cl0.33], respectively. He et al. previously reported the synthesis of Ni–Fe–Y LDH.39 However, in this study, Ni–Fe–Y LDH had a slightly different chemical composition and was used as an electrocatalyst instead of an adsorbent.
Based on of the F− adsorption tests and M2+ leaching analysis in Table S6 in the ESI,† the F− adsorption and M2+ leaching amounts of Ni–Fe–Y-067 LDH were 15.78 mg·g−1 and 3.4 mg L−1, respectively, whereas those of Ni–Cr–Y-067 LDH were 17.09 mg g−1 and 1.5 mg L−1, respectively. These samples exhibited lower M2+ dissolution than Zn–Al–Ga-067, indicating that the LDHs synthesised in the second cycle with two objective variables had greater chemical stability than those produced in the first cycle.
Fig. 5A shows the optimisation process of the F− adsorption and M2+ leaching amounts for the LDHs as functions of the number of experiments. We highlight that the F− adsorption amount fluctuated somewhat but gradually increased, whereas the M2+ leaching amount gradually decreased. Fig. 5B shows the correlation between these variables, where Y = 1 represents the samples from BO with a single objective (F− adsorption amount) and Y = 2 represents the samples from BO with two objectives (F− adsorption and M2+ leaching amounts). Compared with the samples from the first cycle, the samples from the second cycle are plotted in the bottom-right corner of the graph, regardless of whether one or two objective variables were considered. Although Ni–Cr–Y-067 LDH (run 17, Table S6 in the ESI†), which was proposed using two objectives, did not exhibit a higher F− adsorption amount than Ni–Al–Ga-067 LDH (run 10, Table S4 in the ESI†), the M2+ leaching amount of Ni–Cr–Y-067 LDH was lower than that of Ni–Al–Ga-067 LDH, indicating higher chemical stability and confirming the correctness of the present approach. The addition of the M2+ leaching amount as an objective variable allowed for the fabrication of LDH materials with both high F− adsorption capacities and chemical stability. Thus, compared with traditional methods, iterating the experimental condition proposed using BO provides a more cost-effective and efficient method to search for LDH materials with high F− adsorption capacities.
Fig. S3 in the ESI† shows a comparison of the F− adsorption amounts of the LDHs prepared in the present study with those of previously reported adsorbents under similar conditions.6–15 Notably, the LDHs proposed by BO exhibit superior F− adsorption capacities compared with the previously reported adsorbents.
Competitive F− adsorption experiments were then performed in the presence of Cl−, NO3−, HCO3−, and SO42−, according to literature.40–42 We used the synthesised Ni–Al–Ga, Ni–Cr–Y, and Mg–Al LDHs with chemical compositions of Ni0.67Al0.10Ga0.23(OH)2Cl0.33, Ni0.67Cr0.23Y0.10(OH)2Cl0.33, and Mg0.67Al0.33(OH)2Cl0.33, respectively. Ni–Al–Ga, Ni–Cr–Y, and Mg-Al LDHs achieved removal efficiencies of 82.0%, 83.2%, and 71.0%, respectively, with Kd values of 4564, 4951, and 2248 mL g−1, respectively. The higher removal efficiencies and Kd values of Ni–Cr–Y and Ni–Al–Ga LDHs demonstrates their excellent fluoride adsorption performance under competitive adsorption conditions.
To explain the higher chemical stability of Ni–Al–Ga and Ni–Cr–Y LDHs compared with that of Mg–Al LDH, bonding analysis was conducted. Fig. 6 shows the projected crystal orbital Hamilton population (pCOHP) between the divalent cations (M2+) and the neighbouring oxygen atoms in these LDHs. A negative COHP value (or the positive region in –pCOHP) indicates bonding interactions, whereas a positive COHP value (or the negative region in –pCOHP) indicates anti-bonding interactions. The integrated value of COHP up to the Fermi level (iCOHP) quantifies the strength of the bonding interactions between the divalent cations and oxygen atoms. A more negative iCOHP value indicates stronger bonding and higher covalency. Despite the noticeable presence of filled anti-bonding states just below the Fermi level, the Ni–O bond in Ni–Cr–Y LDH has the most negative iCOHP value, followed by that in Ni–Al–Ga. This indicates that the M2+–O bonds in Ni–Al–Ga and Ni–Cr–Y LDHs have a stronger covalent character (Fig. 6a and b). On the other hand, the Mg–O bond in Mg–Al LDH has the least negative iCOHP value, suggesting that it is more ionic in nature, with weaker orbital interactions between Mg and O (Fig. 6c). To further understand the bonding interactions determined from the COHP analysis, the projected density of states of the three LDHs were analysed. As shown in Fig. S4 in the ESI,† the Ni 3d orbitals in Ni–Al–Ga and Ni–Cr–Y LDHs significantly overlap with the O 2p states, particularly in the energy range below the Fermi level. This indicates strong hybridisation between the Ni 3d and O 2p states, which enhances the covalency of the metal–oxygen bonds. In the case of Mg–Al LDH, as Mg primarily consists of s and p states, its orbitals exhibit minimal overlap with the O 2p orbitals. Thus, the higher chemical stability of Ni–Al–Ga and Ni–Cr–Y LDHs can be attributed to the stronger covalent character of the Ni2+–O bonds, whereas the more ionic Mg–O interactions in Mg–Al LDH lead to lower chemical stability.
 | ||
| Fig. 6 COHPs of (a) Ni0.67Al0.10Ga0.23(OH)2Cl0.33, (b) Ni0.67Cr0.23Y0.10(OH)2Cl0.33, and (c) Mg0.67Al0.33(OH)2Cl0.33. | ||
We then discuss the structural stability of the LDHs because several samples proposed by BO failed to produce an LDH structure. We performed an RF analysis to examine the importance of the dataset features (Fig. 7A). The following explanatory variables were considered: heating temperature, holding time, fractions of MI3+ and MII3+, F− adsorption amount, fraction of M2+, ionic radii of M2+, MI3+, and MII3+, electronegativity χ of M2+, MI3+, and MII3+, weighted-average ionic radius, and weighted-average χ. The weighted-average ionic radius accounted for approximately 91% of the total importance, whereas the significance of the other parameters was negligible. These findings indicate that the presence or absence of an LDH structure was significantly influenced by the weighted average of the ionic radius. Visualisation of the weighted-average ionic radius values using the dataset shown in Fig. S5 in the ESI† revealed that samples tended not to exhibit an LDH structure when the weighted-average M2+, MI3+, and MII3+ ionic radius exceeded 0.71 Å. We also examined the effect of the weighted-average M3+ ionic radius of Mg- and Ni-based LDHs on the formation of the brucite-type LDH structure. The results confirmed that this LDH structure does not form when the weighted-average ionic radius of the trivalent cation MI3+/MII3+ exceeds 0.77 Å as summarized in Fig. S6.† These effects of this variable on LDH formation can be explained by considering Mg–Al and Mg–Y LDHs as examples. Fig. 7B shows a schematic diagram of the two-dimensional layer of an LDH viewed from the top. The ionic radii of Mg2+, Al3+, and Y3+ are 0.72, 0.535, and 0.90 Å, respectively.43 As Y3+ has a larger ionic radius than Al3+, the electrostatic repulsion between adjacent metals in Mg–Y LDH (i.e., Mg2+–Y3+ and Y3+–Y3+) is stronger than that between adjacent metals in Mg–Al LDH (i.e., Mg2+–Al3+ and Al3+–Al3+). Thus, suppressing the electrostatic repulsion in the two-dimensional oxide layer is likely important for the formation of the LDH structure.
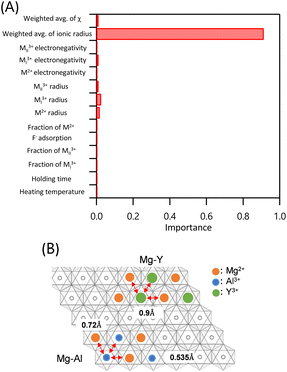 | ||
| Fig. 7 A) RF analysis of explanatory variable importance. B) Schematic diagram of the two-dimensional layer of an LDH viewed from the top. | ||
4. Conclusions
We explored LDH materials with both high F− adsorption capacities and chemical stability using BO with the GPR. The use of one (F− adsorption amount) or two target variables (F− adsorption and M2+ leaching amounts) enabled us to find new LDHs in the extrapolated region of the chemical space. The proposed LDHs, including Ni–Al–Ga, Ni–Fe–Y, and Ni–Cr–Y LDHs, were not present in the original dataset and showed high F− adsorption capacities and chemical stability. The DFT calculation results explained the high chemical stability of the newly discovered Ni-based LDHs. Visualisation revealed that samples with a weighted-average ionic radius exceeding 0.71 tended to lack an LDH structure. The inability to synthesise LDHs may be attributable to significant differences in the ionic radii of the divalent and trivalent metals, resulting in increased electrostatic repulsion between the metal oxide octahedra.Data availability
The authors confirm that the data supporting the findings of this study are available within the article and its ESI.†Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This work was partially supported by the Council for Science, Technology and Innovation (CSTI), Cross-ministerial Strategic Innovation Promotion Program (SIP) in the 3rd period of SIP ‘Creating a materials innovation ecosystem for industrialization’ JPJ012307 (Funding agency: NIMS), and JSPS KAKENHI Grant Number 22H00568.References
- World Health Organization, Guidelines for Drinking Water Quality, Geneva, 2004 Search PubMed.
- A. Chowdhury, M. K. Adak, A. Mukherjee, P. Dhak, J. Khatun and D. Dhak, J. Hydrol., 2019, 574, 333 CrossRef CAS.
- Y. S. Solanki, M. Agarwal, A. B. Gupta, S. Gupta and P. Shukla, Sci. Total Environ., 2022, 807, 333 CrossRef PubMed.
- A. Bhatnagar, E. Kumar and M. Sillanpää, Chem. Eng. J., 2011, 171, 811 CrossRef CAS.
- S. Jagtap, M. K. Yenkie, N. Labhsetwar and S. Rayalu, Chem. Rev., 2012, 112, 2454 CrossRef CAS PubMed.
- F. Ke, G. Luo, P. Chen, J. Jiang, Q. Yuan, H. Cai, C. Peng and X. Wan, J. Porous Mater., 2016, 23, 1065 CrossRef CAS.
- A. Jeyaseelan and N. Viswanathan, ACS ES&T Water, 2022, 2(1), 52 Search PubMed.
- L. H. Velazquez-Jimenez, R. H. Hurt, J. Matos and J. R. Rangel-Mendez, Environ. Sci. Technol., 2014, 48, 1166 CrossRef CAS PubMed.
- K. Pandi and N. Viswanathan, Carbohydr. Polym., 2015, 134, 732 CrossRef CAS PubMed.
- S. Dey, S. Goswami and U. C. Ghosh, Water, Air, Soil Pollut., 2004, 158, 311 CrossRef CAS.
- K. Biswas, K. Gupta and U. C. Ghosh, Chem. Eng. J., 2009, 149, 196 CrossRef CAS.
- E. Kumar, A. Bhatnagar, M. Ji, W. Jung, S. H. Lee, S. J. Kim, G. Lee, H. Song, J. Y. Choi, J. S. Yang and B. H. Jeon, Water Res., 2009, 43, 490 CrossRef CAS PubMed.
- G. Alagumuthu and M. Rajan, Chem. Eng. J., 2010, 158, 451 CrossRef CAS.
- S. M. Prabhu and S. Meenakshi, Carbohydr. Polym., 2015, 120, 60 CrossRef CAS PubMed.
- Q. Chang, L. Zhu, Z. Luo, M. Lei, S. Zhang and H. Tang, Ultrason. Sonochem., 2011, 18, 553 CrossRef CAS PubMed.
- Q. Guo and J. Tian, Chem. Eng. J., 2013, 231, 121 CrossRef CAS.
- T. Wu. L. Mao and L. Wang, RSC Adv., 2015, 5, 23246 RSC.
- C. Ren, M. Zhou, Z. Liu, L. Liang, X. Li, X. Lu, H. Wang, J. Ji, L. Peng, G. Hou and W. Li, Environ. Sci. Technol., 2021, 55, 15082 CrossRef CAS PubMed.
- Q. Wang and D. O'Hare, Chem. Rev., 2012, 112, 4124 CrossRef CAS PubMed.
- S. Miyata, Clays Clay Miner., 1983, 31, 305 CrossRef CAS.
- T. Sudare, S. Tamura, M. Kashiwazaki, Y. Nakamura, K. Kawaguchi, H. Shiiba, K. Fujisawa, M. Tipplook, H. Tanaka, F. Hayashi and K. Teshima, Adv. Mater. Interfaces, 2022, 9, 2201484 CrossRef CAS.
- T. Sudare, K. Kawaguchi, K. Yamaguchi, K. Hirono, M. Tipplook, H. Tanaka, F. Hayashi and K. Teshima, Chem. Mater., 2022, 34, 10681 CrossRef CAS.
- H. Huo, Z. Rong, O. Kononova, W. Sun, T. Botari, T. He, V. Tshitoyan and G. Ceder, Comput. Mater. Sci., 2019, 5, 62 Search PubMed.
- A. Davariashtiyani, Z. Kadkhodaie and S. Kadkhodaei, Commun. Mater., 2021, 2, 115 CrossRef.
- C. E. Rasmussen and H. Nickisch, J. Mach. Learn. Res., 2010, 11, 3011 Search PubMed.
- scikit-learn, sklearn, Gaussian_Process.GaussianProcessRegressor, https://scikit-learn.org/stable/modules/generated/sklearn.gaussian_process.GaussianProcessRegressor.html (accessed Aug 26, 2024) Search PubMed.
- B. Shahriari, K. Swersky, Z. Wang, R. P. Adams and N. de Freitas, Proc. IEEE, 2016, 104, 148 Search PubMed.
- R. Iwama and H. Kaneko, J. Adv. Manuf. Process., 2021, 3, e10085 CrossRef CAS.
- J. Zhang, Y. Huang, G. Ma, Y. Yuan and B. Nener, Cem. Concr. Compos., 2021, 121, 104103 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- A. D. Becke and E. R. Johnson, J. Chem. Phys., 2005, 122, 154104 CrossRef PubMed.
- R. Dronskowski and P. E. Blöchl, J. Phys. Chem., 1993, 97, 8617 CrossRef CAS.
- V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Phys. Chem. A, 2011, 115, 5461 CrossRef CAS PubMed.
- S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, J. Comput. Chem., 2016, 37, 1030 CrossRef CAS PubMed.
- D. He, R.-T. Gao, S. Liu, M. Sun, X. Liu, K. Hu, Y. Su and L. Wang, ACS Catal., 2020, 10, 10570 CrossRef CAS.
- K. K. Yadav, N. Gupta, V. Kumar, S. A. Khan and A. Kumar, Environ. Int., 2018, 111, 80 CrossRef CAS PubMed.
- Z. Bai, C. Hu, H. Liu and J. Qu, J. Colloid Interface Sci., 2019, 539, 146 CrossRef CAS PubMed.
- L. Wei, F. Zietzschmann, L. C. Rietveld and D. V. Halem, Chemosphere, 2020, 243, 125307 CrossRef CAS PubMed.
- R. D. Shannon, Acta Crystallogr., Sect. A, 1976, 32, 751 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ce00313j |
| This journal is © The Royal Society of Chemistry 2025 |