Reactivities of tertiary phosphines towards allenic, acetylenic, and vinylic Michael acceptors

Abstract

The addition of phosphines (PR₃) to Michael acceptors is a key step in many Lewis-base catalysed reactions. The kinetics of the reactions of ten phosphines with ethyl acrylate, ethyl allenoate, ethyl propiolate, ethenesulfonyl fluoride, and ethyl 2-butynoate in dichloromethane at 20 °C was followed by photometric and NMR spectroscopic methods. The experimentally determined second-order rate constants k₂ show that electronic effects in sterically unencumbered phosphines affect their nucleophilicity towards different classes of Michael acceptors in the same ordering. Michael acceptors with sp-hybridised electrophilic centres, however, are less susceptible to changes in the PR₃ nucleophilicity than those with sp²-hybridised reactive sites. Linear correlations of lg k₂ from this work with published rate constants for S_N2 and S_N1 reactions as well as with Brønsted basicities and fugalities for PR₃ demonstrate the generality of the detected reactivity trends. Computed reaction barriers (ΔG^‡_calc) as well as reaction energies (ΔG_add) for Michael adduct formations show excellent correlations with experimentally obtained reaction barriers (ΔG^‡_exp) corroborating the interpretation of the kinetic data and revealing the philicity/fugality features of the reactants in phospha-Michael additions.

---

Introduction

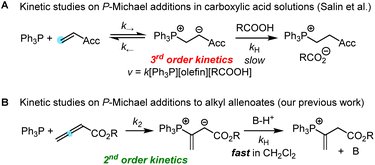
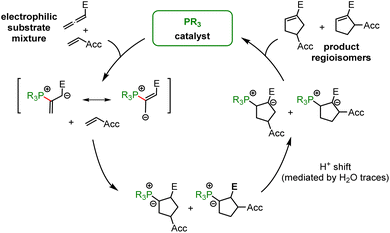
Addition of tertiary phosphines to electron-deficient π-systems generates zwitterionic intermediates which can be trapped directly or after isomerisation with various types of electrophilic reagents for carbon–carbon bond-formation. Thus, Horner's anionic acrylonitrile polymerisation,¹ Rauhut–Currier reactions, Morita–Baylis–Hillman reactions,^2–4 Lu's (3 + 2) cycloadditions, Kwon's [4 + 2] annulations⁵ and many other useful Lewis-base catalysed reactions⁶ share phospha-Michael additions⁷ as initiating steps in their catalytic cycles toward complex, functionalised products.⁸ Chiral phosphine catalysts have enabled enantioselective versions of these transformations.⁹ Though some phospha-Michael additions have recently been exploited for bioorthogonal reactions to detect α,β-unsaturated carbonyl groups in biomolecular targets,¹⁰ the reversibility of the endergonic phosphine additions to Michael acceptors has remained a challenge for kinetic studies.

Protonation of the zwitterionic intermediate is a straightforward approach to render the phospha-Michael addition irreversible. The kinetics of phospha-Michael additions in protic and aprotic solvents with carboxylic acids as the proton sources were carefully investigated by Salin and co-workers (Scheme 1A).^11–14 Generally, rate-determining proton transfer from carboxylic acids to the intermediate zwitterions gave rise to third-order kinetics (Scheme 1A).

Scheme 1 Kinetics of P-Michael additions.

Recently, we studied the kinetics of the adduct formation of PBu₃ and PPh₃ with alkyl and phenyl allenoates in dichloromethane solution.¹⁵ By utilising collidinium triflate and trialkylphosphonium triflates as the proton sources (BH⁺), the intermediate zwitterions were efficiently trapped in fast reactions. It, thus, became possible to determine second-order rate constants k₂ for phosphine additions to allenoates, which allowed us to identify the impact of structural variation on the reactivity of these electrophiles (Scheme 1B).

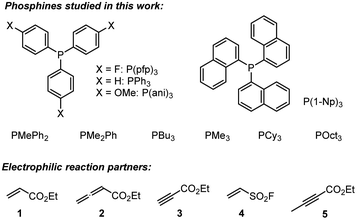
A complementary, systematic comparison of PR₃ reactivities in phospha-Michael additions across different types of Michael acceptors is not available to date.¹⁶ We, therefore, set out to investigate the kinetics of PR₃ additions to allenic, acetylenic and vinylic Michael acceptors. Herein, we present the analysis of the addition kinetics of ten phosphines to ethyl acrylate (1), ethyl allenoate (2), ethyl propiolate (3), ethenesulfonyl fluoride (4), and ethyl 2-butynoate (5) in dichloromethane at 20 °C (Scheme 2), which were followed by photometric and NMR spectroscopic methods. Given that these phosphine additions are generally considered to be the first step in PR₃-catalysed reactions, kinetic investigations will also help to gain further insight into the key factors that control a manifold of organocatalytic reactions. Furthermore, quantum-chemical methods were employed to rationalise the reactivity ordering observed in the kinetic experiments.

Scheme 2 Phosphines PR₃ and electrophiles used in this work (Cy = cyclohexyl).

Results and discussion

Products of the reactions of phosphines with the electrophiles 1–3

Horner and co-workers showed that stable, zwitterionic phospha-Michael adducts are obtained when PEt₃ or PPh₃ are combined with highly reactive Michael acceptors, such as 1,1-dicyanoethene.¹ They noted, however, that the less Lewis acidic benzylidenemalononitrile (BMN) only forms Lewis adducts with trialkylphosphines (PMe₃, PEt₃, and PBu₃) but not with PPh₃. Photometric studies of the isolated adduct of benzylidenemalononitrile and PEt₃ surprisingly showed that the UV-vis spectrum was identical to benzylidenemalononitrile alone. Horner explained this experimental observation by the dissociation of the Michael adduct in solution.¹

Efficient trapping of the initially formed zwitterionic phospha-Michael adducts is, therefore, a prerequisite to get to observable reaction products in solution and to generate conditions for reproducible kinetic measurements. Hence, we started our preparative investigations by NMR characterisations of relevant protonated Michael adducts.

The Michael addition of PPh₃ to acrylate 1 was first reported by Hoffmann, who used triphenylphosphine hydrobromide that reacted with ethyl acrylate (1) within 15 min in acetonitrile.¹⁷ We used pre-formed triphenylphosphonium triflate (TPPT) to characterise the products of its reactions with the electrophiles 1–4 by NMR spectroscopic and HRMS methods (Scheme 3).

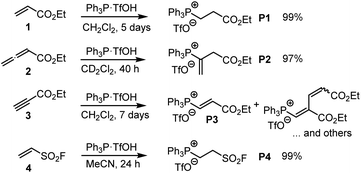Scheme 3 Generation of phosphonium triflates P1–P4 by reaction of PPh₃·TfOH (TPPT) with the Michael acceptors 1–4 (at ambient temperature).

TPPT reacted slowly but selectively with ethyl acrylate (1) to furnish within five days almost quantitatively the phosphonium triflate P1, which was isolated in a yield of 99%.¹⁸ The analogous reaction of TPPT with ethyl allenoate (2) in CD₂Cl₂ generated the vinylphosphonium triflate (P2) in a yield of 97%.¹⁵ The reaction of TPPT with Michael acceptor 3 mainly produced the acceptor-substituted vinyl phosphonium salts P3. The NMR spectra and in particular the HRMS analytical data showed that also 2 : 1 products (as a mixture of E- and Z-isomers) were formed in significant amounts, which could not be separated from the 1 : 1 adduct P3. Ethenesulfonyl fluoride (ESF, 4) is a considerably stronger electrophile than 1–3. Accordingly, 4 reacted already within 24 h quantitatively with TPPT to yield the phosphonium triflate P4 (99% yield of isolated product).

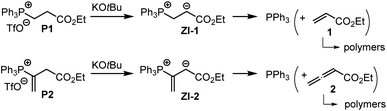
The associations of triphenylphosphine with Michael acceptors 1–4 are highly reversible if the reactions are performed without an appropriate proton source that efficiently traps the incipient, zwitterionic Lewis adducts. Attempts to generate the zwitterions ZI-1 and ZI-2 by deprotonation of the phosphonium salts P1 and P2, respectively, with potassium t-butoxide in d₆-DMSO gave rise to rapid retro-Michael additions (Scheme 4). The release of free PPh₃ from P1 and P2 was unequivocally detected by ¹H, ¹³C, and ³¹P NMR spectroscopic analysis of the reaction mixtures (ESI, Fig. S19–S24†). The electrophiles 1 and 2 cannot be recovered under these reaction conditions. However, owing to a lack of NMR signals in the olefinic region and the occurrence of various new resonances in the aliphatic region, we assume that 1 and 2 rather undergo anionic polymerisations. These observations indicate that Lewis acid/base adduct formation between triphenylphosphine and the Michael acceptors 1 or 2 are endergonic.

Scheme 4 Retro-Michael additions of P1 and P2 under basic reaction conditions (in d₆-DMSO).

To investigate the kinetics of the first step of the phosphine-catalyzed reactions with Michael acceptors, we have, therefore, decided to combine phosphines PR₃ with the relevant electrophiles in the presence of proton sources that are able to intercept the initially formed zwitterions by fast protonation. The next section, therefore, shows how we identified Brønsted acids that reliably trapped the zwitterionic adducts but did not influence the reactivities of two reaction partners in the phospha-Michael addition.

Choice of proton sources as trapping reagents for the intermediate zwitterions

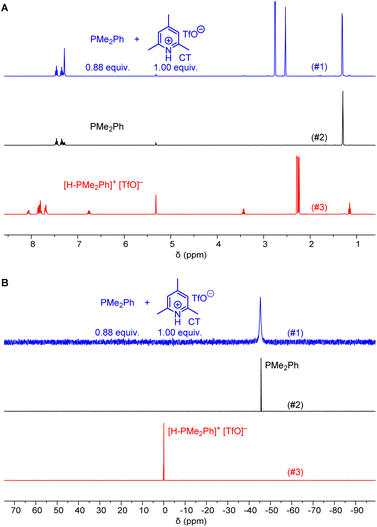
Ohmori and colleagues showed that the reaction of PPh₃ with 1 (in CH₂Cl₂) can be performed under neutral conditions when 2,6-lutidinium perchlorates or tetrafluoroborates are used as proton sources.¹⁹ Lutidinium ions are only weak acids (pK_a = 14.16 in MeCN)²⁰ and it can be expected that they are neither able to protonate PPh₃ (pK_aH = 7.62 in MeCN)²⁰ nor the Michael acceptor 1.

Given that we needed a proton source to cover the Brønsted basicity range from P(pfp)₃ to PMe₂Ph (pK_aH = 12.64 in MeCN) without affecting the reactivity of the phosphines, we expected that the even less acidic 2,4,6-collidinium triflate (pK_a = 15.00 in MeCN)²⁰ would be a practical trapping reagent for kinetic measurements. NMR spectroscopic studies in CD₂Cl₂ were carried out to assess whether the known relative acidities in acetonitrile are transferable to those in dichloromethane solution. The ¹H NMR spectrum of a mixture of PMe₂Ph with a slight excess of 2,4,6-collidinium triflate (CT) showed only resonances that could be assigned to both individual components in the mixture. Resonances for the phenyl group in [H-PMe₂Ph]⁺ at δ > 7.5 ppm were not detected, and also the CH₃ resonance of PMe₂Ph at δ = 1.31 ppm did not shift when mixed with CT (Fig. 1A). Accordingly, the ³¹P NMR spectrum of a mixture of CT with PMe₂Ph (0.9 equiv.) in CD₂Cl₂ showed that the detected chemical shift (δ_P = −45.6 ppm) corresponds to free PhMe₂P and is not shifted towards the resonance for the protonated form (δ_P = 0.0 ppm, Fig. 1B). An analogous ¹H and ³¹P NMR study for a mixture of the less basic PMePh₂ (pK_aH = 9.97 in MeCN)²⁰ and CT is presented in the ESI (Fig. S3 and S4†) and shows, accordingly, that CT does not protonate PMePh₂ in dichloromethane.

Fig. 1 (A) 400 MHz ¹H and (B) 162 MHz ³¹P{¹H} NMR spectra of a mixture of collidinium triflate (CT) and PMe₂Ph in CD₂Cl₂ (#1 in blue) compared to the ¹H and ³¹P{¹H} NMR spectra of PMe₂Ph (#2 in black) and dimethylphenylphosphonium triflate (#3 in red).

Further NMR studies were carried out to elucidate possible interactions of CT additives with the Michael acceptors 1–3. Fig. S7–S9† (ESI) illustrate that the ¹H NMR chemical shifts of the acrylate 1, the allenoate 2, and the propiolate 3, respectively, did not undergo changes when mixed with CT in CD₂Cl₂. The resonances assigned to CT remained unchanged, which indicates that this proton source does not interact with the electrophiles. Given that interactions of CT were neither observable with the electrophilic Michael acceptors 1–3 nor with those phosphines PR₃ with basicities lower than that of PMe₂Ph (pK_aH < 12.64 in MeCN), it can be expected that CT will be a suitable zwitterion intercepting reagent for kinetic experiments in dichloromethane solution.

Kinetic measurements for reactions of electrophiles with the more basic trialkylphosphines PMe₃, PCy₃ and POct₃ were carried out by in situ liberation of a certain amount of free PR₃ from trialkylphosphonium triflates by adding known amounts of the strong Brønsted base triethylamine (TEA) to the solutions in dichloromethane. The detection of only a single ³¹P NMR signal (in CD₂Cl₂) indicates quantitative deprotonation of [H-PR₃]⁺ by TEA (ESI, Fig. S16–S18†). By using the thus generated solutions, the reversibly formed adducts of the reactions of the electrophiles 1–3 with PMe₃, PCy₃ and POct₃, respectively, were efficiently trapped by the conjugate Brønsted acids of the studied PR₃ nucleophiles. Because handling and further dilution steps of the trialkylphosphine stock solutions were avoided by this procedure, also oxidation prone PR₃ could be studied under reliable conditions and delivered reproducible kinetic data.

Comparing the heats of formation for the parent allene (Δ_fH = +192.1 kJ mol⁻¹) with that for propyne (Δ_fH = +185.4 kJ mol⁻¹) shows that the alkyne is the thermodynamically favored isomer.²¹ We, therefore, tested whether the allene derivative 2 can isomerise to the acetylene derivative 5 under the conditions of the kinetic experiments. The ¹H NMR spectra of TEA + 2 and TEA + 5 mixtures in CD₂Cl₂, which were stored at ambient temperature overnight (ESI, Fig. S11 and S12†), remained unchanged, however, indicating that free TEA is not able to equilibrate the allenoate 2 with the corresponding alkynoate tautomer 5, or vice versa.

Furthermore, comparing ¹H NMR spectra of the mixtures of triethylammonium triflate (TEAT), which is generated during the in situ liberation of PR₃, and Michael acceptors 1, 2, and 5 (in CD₂Cl₂) with those of the individual compounds in the same solvent showed that TEAT (possible proton source) does not interact with the electrophiles 1, 2, and 5 (ESI, Fig. S13–S15†). Interestingly, also mixtures of tributylphosphonium triflate (TBPT) with ethyl acrylate (1) show ¹H NMR spectra, which reflect the resonances of the individual compounds (ESI, Fig. S10†), thus excluding significant electrophile activation by the presence of the TBPT proton source.

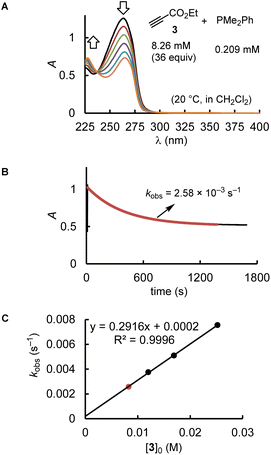
Kinetics

Depending on the spectroscopic properties of the reagents, the kinetics of PR₃ additions to the electrophiles 1–3 were monitored by using either photometry or NMR spectroscopy.

The majority of the kinetics of reactions of 2 and 3 with phosphines in dichloromethane at 20 °C were determined by following absorption changes in the UV-range. For a straightforward evaluation of the absorption decay curves, we used one of the reaction partners in at least 10-fold excess relative to the initial concentration of the minor compound. This made it possible that first-order rate constants k_obs (s⁻¹) could be derived from fitting the mono-exponential function A = A₀ exp(−k_obst) + C to the experimentally observed decrease of the absorption of the minor compound. Determination of k_obs at four different concentrations of the excess reaction partner enabled us to calculate the second-order rate constants k₂ (M⁻¹ s⁻¹) from the slope of the linear regression line of k_obsvs. [PR₃]₀ or [electrophile]₀. Furthermore, the linearity of both types of plots, that is, k_obsvs. [PR₃]₀ and k_obsvs. [electrophile]₀, indicates the operation of a rate law for the overall reaction, which is first order in [PR₃] and first order in [electrophile].

Fig. 2 uses the relatively slow reaction of 3 with PMe₂Ph to illustrate the workflow for kinetic measurements by conventional photometric equipment and their subsequent evaluation. The kinetics of faster reactions (t_1/2 < 40 s) were followed by using stopped-flow spectrophotometer systems and analysed analogously. The sequential mixing option of the stopped-flow instrument was used to study the kinetics of the fast reactions of PMe₃ with the electrophiles 1, 2, and 4. At mixer 1, PMe₃ was liberated by deprotonation of trimethylphosphonium tetrafluoroborate with a substoichiometric amount of TEA. The thus prepared nucleophile solution was then mixed at mixer 2 with the solution of 1, 2, or 4. Details for the individual kinetics are given in the ESI.†

Fig. 2 (A) The decay of the UV absorption of PMe₂Ph was used to monitor the kinetics of the reaction of PMe₂Ph with ethyl propiolate (3) in CH₂Cl₂ under pseudo first-order conditions (proton source: CT, [CT]₀ = 0.232 mM). (B) Exponential decay of the absorption A at 252 nm during the reaction. (C) Determination of the second-order rate constant k₂ (M⁻¹ s⁻¹) from the slope of a linear correlation of k_obs (s⁻¹) vs. [3]₀.

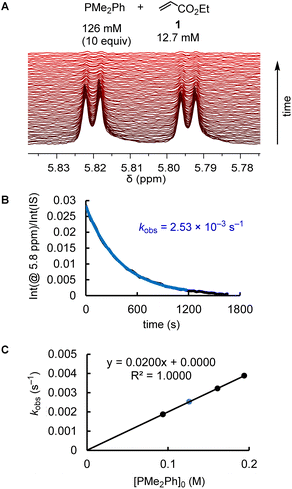
The kinetics of further phosphine–electrophile reactions, in particular those which involved phosphines with aryl groups, were more accessible through the use of NMR techniques.²² Tracing the time-dependent changes in the ¹H NMR spectra was used, for example, to follow the kinetics of the PMe₂Ph addition to ethyl acrylate (1) (Fig. 3). CT trapped the intermediate zwitterions. Added mesitylene served as the internal integration standard. The experiment shown in Fig. 3A was repeated at different CT concentrations at otherwise identical conditions. For [CT] = 21.4, 37.1, and 73.3 mM, the observed first-order rate constants k_obs were 2.53 × 10⁻³, 2.47 × 10⁻³, and 2.55 × 10⁻³ s⁻¹, respectively (ESI, Table S10†). An analogous independency of k_obs in the reaction of PBu₃ + 1 was observed when enhancing the TBPT concentration (ESI, Table S11†). Thus, in accord with the previous NMR investigations on binary CT (or TBPT) mixtures with either phosphines or electrophiles, the observed rate constant k_obs remained unchanged within the experimental error limit, which corresponds to a zeroth order kinetics with regard to the concentration of the proton source. This observation underpins again that the nature of the proton sources selected in this work did not affect the kinetics of the phospha-Michael additions we aimed to investigate.

Fig. 3 (A) Monitoring the kinetics of the PMe₂Ph addition to ethyl acrylate (1) in CD₂Cl₂ (20 °C) by ¹H NMR spectroscopy (proton source: CT, [CT]₀ = 21.4 mM). (B) Exponential decay of the integrals for the olefinic protons at 5.8 ppm during the progress of the reaction (mesitylene was used as an internal integration standard, IS). (C) Determination of the second-order rate constant k₂ (M⁻¹ s⁻¹) from the slope of a linear correlation of k_obs (s⁻¹) vs. [PMe₂Ph]₀.

Phosphines PR₃ were used as the excess compounds when the decay of the electrophile was followed by ¹H NMR spectroscopy (Fig. 3). An inverse concentration ratio, that is, with the electrophiles as the excess compounds, was employed for ³¹P NMR kinetic measurements. The kinetics for the combinations of PMePh₂ with 1 gave k₂ = 1.66 × 10⁻³ M⁻¹ s⁻¹ by ¹H NMR (ESI, Table S9†) and k₂ = 2.36 × 10⁻³ M⁻¹ s⁻¹ by ³¹P NMR spectroscopy (ESI, Table S8†), which agree within a factor of 1.4. Reaction monitoring of the kinetics of P(pfp)₃ with ethyl allenoate (2) gave a k₂(³¹P)/k₂(¹H) ratio of 1.1 (ESI, Tables S16 and S17†). For the reactions of PPh₃ with ethyl propiolate 3 (ESI, Tables S28 and S29†), ¹H NMR spectroscopy delivered a slightly higher k₂ value than the ³¹P NMR spectroscopic reaction tracing [k₂ = 1.04 × 10⁻² M⁻¹ s⁻¹ (¹H) vs. 7.05 × 10⁻³ M⁻¹ s⁻¹ (³¹P)]. In general, we considered rate constants determined by time-resolved ¹H NMR spectroscopy to be more reliable than results from ³¹P NMR spectroscopic reaction monitoring because ¹H NMR spectra were recorded with an internal integration reference. In subsequent correlations we, therefore, preferred to use k₂ from ¹H NMR kinetics if k₂ for a given PR₃ + electrophile pair was determined by both ¹H and ³¹P NMR kinetics.

To further test the influence of the zwitterion trapping on the kinetics, we used two different proton sources (CT and TEAT) when following the kinetics of the reaction of PPh₃ with ethyl acrylate (1) by ³¹P NMR spectroscopy (Table 1, entries 1 & 2). The individual linear correlations of k_obs with [1]₀ agreed so surprisingly well that we used the first-order rate constants from both series of kinetic measurements jointly to determine the second-order rate constant k₂ for the PPh₃ + 1 reaction (ESI, Table S6†).

Table 1 Comparison of the kinetics of phospha-Michael additions (dichloromethane, 20 °C) with variable zwitterion trapping reagents

Entry	Reactions	Trapping reagents	k 2 ^a (M^−1 s^−1)
a Determined by time-resolved ^31P NMR spectroscopy. b Determined by photometric methods.
1	PPh3 + 1	CT	1.55 × 10^−4^a
2	PPh3 + 1	TEAT	1.56 × 10^−4^a
3	PBu3 + 1	TBPT	5.83 × 10^−2^b
4	PBu3 + 1	BMN	5.47 × 10^−2^b
5	PMe2Ph + 3	CT	0.292^b
6	PMe2Ph + 3	BMN	0.257^b

---

In a next step, we sought to replace the proton source by an olefinic Michael acceptor, that is, a neutral carbon-centred electrophile. The highly electrophilic BMN (Mayr E = −9.42)²³ was used by Lu and coworkers as a reaction partner for alkyl allenoates 2 in PPh₃-catalysed cyclopentene syntheses.²⁴ Recently, we could demonstrate that BMN reacts fast yet reversibly with PBu₃.¹⁵ Generation of cycloadducts, therefore, requires initial PBu₃ attack at the allenoate electrophile to be productive. Entries 3 and 4 in Table 1 show that the second-order rate constants k₂ for reactions of ethyl acrylate (1) with PBu₃ are identical (within an error margin of ±10%) and independent of whether proton (TBPT) or BMN trapping was used. Similar rate constants k₂ (within ±10%) were also derived for the reaction of ethyl propiolate (3) with PMe₂Ph when CT and BMN were compared as trapping reagents (entries 5 & 6). The results in Table 1, thus, corroborate that the proton sources used in the kinetic standard procedure to generate the data for Table 2 neither attenuated the reactivity of the PR₃ nucleophiles nor enhanced the electrophilicity of the esters 1 and 3 by protonation.

Table 2 Second-order rate constants k₂ for the reactions of phosphines PR₃ with the Michael acceptors 1–5 (in dichloromethane, at 20 °C)

Phosphines PR3	k 2 ^a (M^−1 s^−1)
	Ethyl acrylate (1)	Ethyl allenoate (2)	Ethyl propiolate (3)	ESF (4)	Ethyl 2-butynoate (5)
a In CH2Cl2, kinetics followed by photometric methods if not mentioned otherwise. b In CD2Cl2, kinetics followed by online ^31P NMR spectroscopy. c In CD2Cl2, kinetics followed by online ^1H NMR spectroscopy. d For the reaction of 2 with PPh3 in benzene activation parameters ΔH^‡ = 14.8 kcal mol^−1 and ΔS^‡ = −19.6 cal mol^−1 K^−1 were reported in ref. 25, which correspond to a second-order rate constant of k2 = 2.9 × 10^−3 M^−1 s^−1 (20 °C).
P(pfp)3	2.22 × 10^−5^b	3.43 × 10^−3^c	2.86 × 10^−3^c	4.23 × 10^−1	n.d.
PPh3	1.55 × 10^−4^b	7.67 × 10^−3^c^,^d	1.04 × 10^−2^c	3.38	2.05 × 10^−5^b
P(ani)3	9.32 × 10^−4^b	3.76 × 10^−2	5.45 × 10^−2	n.d.	n.d.
PMePh2	1.66 × 10^−3^c	6.12 × 10^−2	6.28 × 10^−2	8.76	n.d.
PMe2Ph	2.00 × 10^−2^c	2.68 × 10^−1	2.92 × 10^−1	4.26 × 10^2	n.d.
PBu3	5.83 × 10^−2	6.35 × 10^−1	9.61 × 10^−1	7.99 × 10^2	5.71 × 10^−3^c
PMe3	1.24 × 10^−1	9.69 × 10^−1	9.56 × 10^−1	2.07 × 10^3	n.d.
PCy3	3.82 × 10^−2^c	1.20 × 10^−1	1.43	n.d.	n.d.
POct3	5.45 × 10^−2	7.24 × 10^−1	2.69	n.d.	n.d.
P(1-Np)3	Too slow^b	8.00 × 10^−6^b	8.46 × 10^−5^b	n.d.	n.d.

---

Table 2 gathers the second-order rate constants k₂ for the reactions of the phosphines PR₃ with the electron-deficient π-systems in 1, 2, and 3.²⁵ In addition, the kinetics of PR₃ reactions with ESF (4) were included in the study. ESF (4) is a Michael acceptor that is known to be considerably more electrophilic than ethyl acrylate 1.²⁶ Furthermore, we investigated the reactivity of ethyl 2-butynoate (5), an isomer of 2, towards PBu₃ and PPh₃.

As illustrated in Fig. 4, the second-order rate constants k₂ in Table 2 show that ethyl acrylate (1) is a relatively weak electrophile towards phosphines PR₃. The reactivities of PR₃ towards ethyl allenoate (2) and ethyl propiolate (3) are at almost the same levels and generally exceed those towards ethyl acrylate (1) by one to two orders of magnitude. The reactivity of the terminal alkynyl π-system in the ethyl ester 3 is reduced by 2.5 to 3 orders of magnitude if a methyl substituent is added, as shown by the entries for ethyl 2-butynoate (5), which is even by a factor of 10 less reactive towards phosphines PR₃ than ethyl acrylate (1).

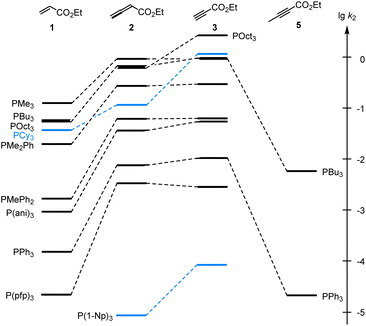Fig. 4 Reactivities of PR₃ towards the Michael acceptors 1, 2, 3, and 5 compared by the second-order rate constants (lg k₂) for the formation of Michael adducts in dichloromethane at 20 °C (data from Table 2).

Significant changes in the relative order of PR₃ reactivities are only observed for the sterically demanding phosphine PCy₃,²⁷ which catches up in reactivity with other trialkylphosphines when it adds to the terminal electrophilic carbons in 1 or 3. However, PCy₃ reacts considerably slower than other trialkylphosphines with 2, in which the electrophilic reaction centre is the central carbon in the allene π-system and thus more difficult to access for the bulky PCy₃ than for the sterically less demanding phosphines PMe₃, PBu₃ or POct₃. As a consequence, rate constants for reactions of PCy₃ were generally excluded in the subsequent correlation analyses, which were performed to gain further quantitative insight in structure–reactivity relationships for Michael additions of phosphines PR₃. The same reasons that explain the k₂(3)/k₂(2) = 12 for PCy₃ can be applied to rationalise the by one order of magnitude higher reactivity of P(1-Np)₃ towards 3 (terminal electrophilic centre) than towards 2.

Correlation analysis

Reactivities of Michael acceptors. The decadic logarithm of the second-order rate constants (lg k₂) of the reactions with ethyl acrylate (1) can be used as a reference to compare the susceptibilities of the different types of electrophiles for variation of the phosphine reactivities. Fig. 5 shows that the relative trends are identical when changing from the sp²-hybridised electrophilic centre in 1 to the sp-hybridised reactive positions in 2 or 3. The slopes of 0.686 and 0.747 for the correlations with 2 and 3, respectively, illustrate however, that the increase in phosphine reactivity towards Michael acceptor 1 is only partially found in the faster reactions with the electron-deficient π-systems in 2 and 3. The lower susceptibility is not a consequence of the Reactivity-Selectivity-Principle, a concept that has been criticised several times before.²⁸ This can be demonstrated through reactions of the phosphines PR₃ with ESF (4), which are much faster than those with 1, 2, or 3. Yet, the linear plot of lg k₂(4) vs. lg k₂(1) shows constant selectivity (slope = 0.985). Rather, we interpret the different slopes in Fig. 5A–C to be a result of the different hybridisation of the electrophilic centres, which differentiate the sp²-hybridised reactive sites in 1 and 4 from those in the sp-hybridised 2 and 3.

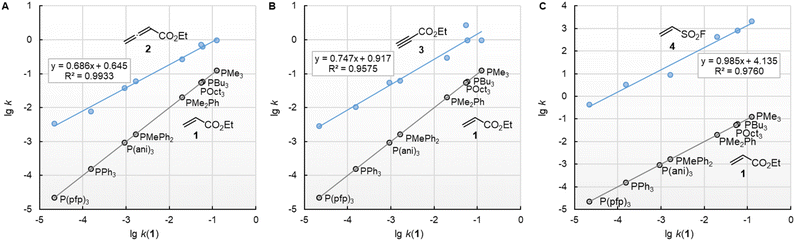Fig. 5 Relative reactivities of PR₃ towards (A) ethyl allenoate (2), (B) ethyl propiolate (3), and (C) ESF (4) referenced towards lg k(PR₃ + 1). With rate constants k₂ from Table 2, data for the sterically encumbered PCy₃ was excluded when constructing the correlation lines.

Correlation with Brønsted basicities of phosphines. Comparison with published physico-chemical data (Table 3) or reactivity descriptors for PR₃ shows that the relative reactivity ordering for tertiary phosphines derived from reactions with the Michael acceptors 1–3 (cf.Table 2) is also reflected by other reaction series.^20,29–32

Table 3 Comparison of the reactivity of phosphines PR₃ towards Michael acceptors 1–3 (in dichloromethane, at 20 °C) with their basicity (pK_aH), nucleophilicities in reactions with ethyl iodide (EtI) and iron-complex stabilised carbocations (N_Fe), ligand exchange rate constants at borane (log k^F_B), and methyl cation affinities (MCA)

PR3	lg k2			pKaH^a	lg k2(EtI)^b	N Fe ^c	lg k^FB^d
	1	2	3
a Acidities of R3P^+H refer to H2O as reported in ref. 29a and 30, values in parentheses are acidities of R3P^+H in MeCN as reported in ref. 20. b Calculated from second-order rate constants k2 (M^−1 s^−1) for reactions of PR3 with ethyl iodide in acetone at 35 °C reported in ref. 29b. c Phosphine nucleophilicities NFe towards iron-complex stabilised carbocations from ref. 31. d Calculated from the rate constants k^FB (M^−1 s^−1) for the ligand exchange of R3P in R3P→BH3 complexes by quinuclidine in toluene at 30 °C reported in ref. 32. e N Fe of PEt2Ph is used because NFe for PMe2Ph has not been determined. f Calculated by DFT methods (ESI).
P(pfp)3	−4.65	−2.46	−2.54	1.97	—	1.3	−2.17
PPh3	−3.81	−2.12	−1.98	2.73 (7.62)	−4.42	1.95	−2.59
P(ani)3	−3.03	−1.42	−1.26	4.57 (10.06)	−3.57	2.9	−3.47
PMePh2	−2.78	−1.21	−1.20	4.65 (9.97)	—	—	−3.46
PMe2Ph	−1.70	−0.57	−0.53	6.49 (12.64)	−3.12	(3.3)^e	−4.46
PBu3	−1.23	−0.20	−0.02	8.43	−2.79	3.6	−5.59
PMe3	−0.91	−0.01	−0.02	8.65 (15.48)	−2.65	—	−5.44
PCy3	−1.42	−0.92	+0.16	9.70	−2.68	—	−5.60
POct3	−1.26	−0.14	+0.43	9.03^f	—	—	—

---

The nucleophilic reactivities of amines towards C-centred electrophiles have repeatedly been reported to correlate only poorly with their Brønsted basicities (pK_aH).^33,34 In contrast, the second-order rate constants for the attack of phosphines PR₃ at Michael acceptors 1–3 in dichloromethane are linearly related to the phosphine basicities in water (Fig. 6). PCy₃ deviates negatively from the correlation lines constructed for the remaining PR₃ nucleophiles, and the reaction of PCy₃ with the allenoate 2 is by more than a factor of 10 slower than expected based on its pK_aH. The deviation of PCy₃ from the correlation lines is less prominent for both electrophiles with a terminal reaction centre. Because available data for pK_aH(MeCN) and pK_aH(H₂O) of PR₃ correlate linearly (r² = 0.9997, n = 5, ESI, Fig. S1†), we can assume that correlations of our reactivity data with pK_aH(H₂O) will also hold in aprotic polar solvents and will allow chemists to predict the reactivities of further sterically unencumbered phosphines towards neutral electrophiles. The slopes in the range of 0.49 to 0.34 indicate that only a part of the thermodynamic driving force of the protonation reactions is seen in the kinetics of PR₃ additions to Michael acceptors.

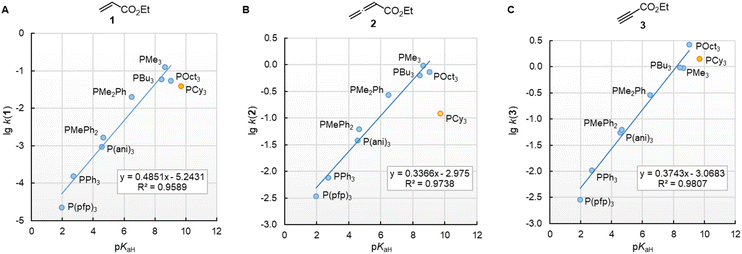Fig. 6 Linear relationships of the second-order rate constants (lg k₂, at 20 °C in dichloromethane) for reactions of R₃P with the Michael acceptors (A) ethyl acrylate (1), (B) ethyl allenoate (2), and (C) ethyl propiolate (3) and the Brønsted basicities pK_aH(H₂O) of the phosphines R₃P (with data from Table 3, data for the sterically encumbered PCy₃ excluded when constructing the correlation lines).

Correlation with nucleophilicities of phosphines in S_N1 and S_N2 reactions. The nucleophilicity of PR₃ phosphines was previously characterised by investigating the kinetics of ethylation reactions (with ethyl iodide) in acetone at 35 °C (Table 3).^29b The rate constants that we determined in this work for addition reactions of PR₃ to electron-deficient neutral π-systems correlate linearly with the S_N2 reactivities of tertiary phosphines towards ethyl iodide, lg k(EtI) (Fig. 7). For the electrophiles 1 and 3, the data point of PCy₃ is close to the respective correlation line, which illustrates the similar steric demand for reactions of PR₃ at terminal –CH₂X, =CH₂, and ≡CH groups. The slope of the correlation line is 1.7 for the olefinic Michael acceptor 1 (Fig. 7A), close to the typical slope of 2 observed when comparing nucleophile reactivities in S_N1 reactions with those in S_N2 reactions.^35–37 The correlation lines for the sp-hybridised electrophiles 2 and 3 are more shallow. Their slopes in the range of 1.2 (Fig. 7B/C) are caused by the higher degree of reorganisation required to change the hybridisation at the reaction centre from a linear to a trigonal planar geometry.

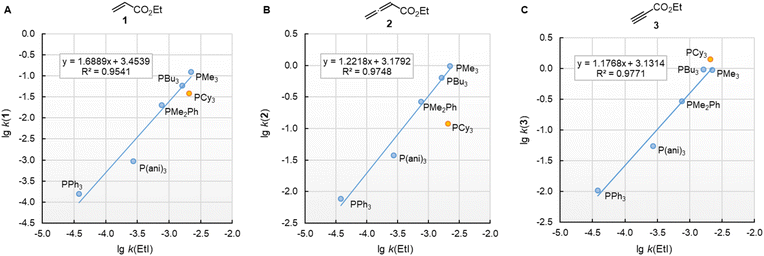Fig. 7 Reactivities (lg k₂) of PR₃ towards (A) ethyl acrylate (1), (B) ethyl allenoate (2), and (C) ethyl propiolate (3) correlate linearly with the S_N2 reactivity of PR₃ towards ethyl iodide (in acetone at 35 °C, ref. 29b). With rate constants k₂ from Table 3, data for the sterically encumbered PCy₃ excluded when constructing the correlation lines.

Furthermore, rate constants of addition reactions of phosphines PR₃ to iron-complex stabilised carbocations, such as [Fe(CO)₃(C₆H₇)]⁺, were reported.^31,38 These kinetic data were used by Kane-Maguire, Honig, and Sweigart to derive N_Fe parameters (Table 3), which describe the averaged nucleophilicity of a PR₃ reagent towards such cationic complexes.³¹ The graphs in Fig. 8 demonstrate that the phosphine reactivities determined for reactions with 1, 2, and 3 are linearly related with the N_Fe descriptors.

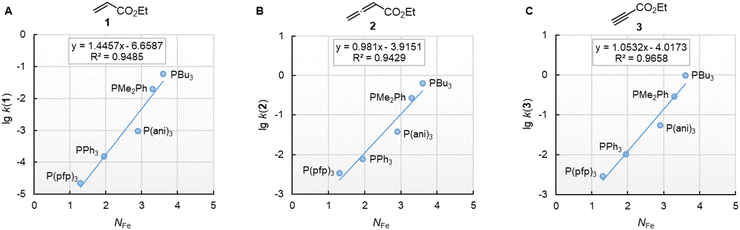Fig. 8 Reactivities (lg k₂) of PR₃ towards (A) ethyl acrylate (1), (B) ethyl allenoate (2), and (C) ethyl propiolate (3) correlate linearly with N_Fe, which are nucleophilicity parameters for phosphines derived from reactions of PR₃ with cationic electrophiles structurally similar to [Fe(CO)₃(C₆H₇)]⁺, from ref. 31 and 38 With rate constants k₂ from Table 3. For the PMe₂Ph entries, the N_Fe of PEt₂Ph was used. The correlation for ESF (4) is shown in Fig. S2 (ESI).†

Thus, the rate constants determined in this work for the reactions of PR₃ phosphines with neutral Michael acceptors correlate both with reported phosphine reactivities towards S_N2 and S_N1 substrates. Given that the molecular structures of ethyl iodide and [Fe(CO)₃(C₆H₇)]⁺ ion are unlike the Michael acceptors studied in this work, we can conclude that the reactivities of the PR₃ nucleophiles determined towards Michael acceptors 1–3 are generally applicable.

Correlation with borane-nucleofugalities of phosphines. There is no general relationship between nucleophilicity and nucleofugality (or Lewis basicity).³⁹ Several classes of nucleophiles, such as DABCO,^40,41 other tertiary alkylamines,³⁴ thioethers,⁴² or iodide and cyanide ions, have been reported to be good nucleophiles and excellent nucleofuges owing to their little need for reorganisation and low Marcus intrinsic barriers.⁴³ However, other classes of compounds are good nucleophiles but weak nucleofuges.⁴⁴ Quite often, only a few experimentally determined data exist for either of the two reaction directions. As a consequence, assessing Marcus intrinsic barriers is impossible and predictions of philicity/fugality relationships become infeasible.

The isoelectronic relation between H₃C-X and [H₃B-X]⁻ triggered our interest to compare the reactivities of the phosphines PR₃ at carbon with those at boron centres. Recently, Lloyd-Jones and colleagues studied the rate constants of quinuclidine displacement of R₃P–BH₃ adducts in toluene at 30 °C.³² They reported mechanistic evidence consistent with an S_N2-like process at the boron-centre. The Lloyd-Jones group also derived an increment system of ‘ligand nucleofugality values 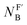for phosphines PR₃ to describe the structural factors that influence the leaving group abilities. The N^F_B values correlate excellently with the pK_aH values of PR₃ in water. The linear relationship spans over a range of 11 pK_a units (n = 12, r² = 0.9956) and comprises P(pfp)₃ as the least basic and PCy₃ as the most basic phosphine.³²

In this work, we found that also the reactivities of phosphines towards Michael acceptors correlate linearly with their pK_aH values (cf.Fig. 6). Thus, the stage was set for establishing a relationship between nucleophilicities and nucleofugalities of PR₃ by combining the rate constants for adduct formation of PR₃ with Michael acceptors with the rate constants for the quinuclidine displacement of PR₃ in R₃P-borane complexes (k^F_B).³²Fig. 9 shows an inverse linear correlation for the phosphines in both reaction series. The weakest nucleophile P(pfp)₃ is the most reactive nucleofuge, and the relation is vice versa for the highly nucleophilic PMe₃ or PBu₃. Depending on the steric environment at the electrophilic centres of the Michael acceptors, PCy₃ is close to the linear correlation for the sterically unencumbered PR₃ species (as for 1 and 3) or has been determined to be a weaker nucleophile than expected on the basis of its nucleofugality lg k^F_B (as for 2).

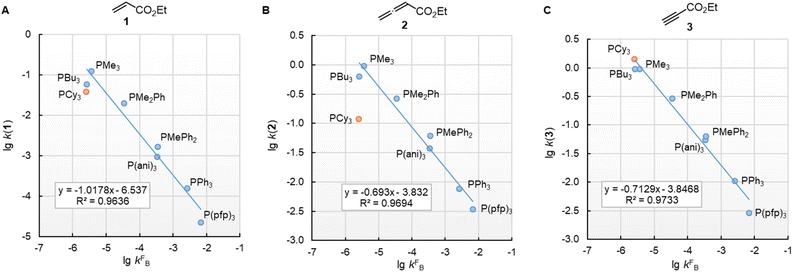Fig. 9 Correlation of PR₃ reactivity (lg k₂ in dichloromethane) towards (A) ethyl acrylate (1), (B) ethyl allenoate (2), and (C) ethyl propiolate (3) with the ligand nucleofugality of R₃P from R₃P→BH₃ complexes (external nucleophile: quinuclidine, in toluene at 30 °C) from ref. 32. With rate constants k^F_B from Table 3, data for PCy₃ excluded when constructing the correlation lines.

Quantum-chemical analysis

Previous quantum-chemical studies of the PMe₃/methyl allenoate addition in benzene gave significantly different results: the addition was reported to be almost thermoneutral^45b or endergonic (ΔG_add = +40.6 kJ mol⁻¹).^25,45a This ambiguity in calculating the driving force of a relatively simple model reaction is an indication of the importance of the computational methods used. Hence, we started by investigating the influence of quantum-chemical methods on the thermodynamics of the PMe₃ addition to ethyl allenoate (2) by using different basis sets, electronic structure methods, and solvation models (see ESI† for details). We found that the combination of the MN15 functional with the triple-ζ basis set def2-TZVPP and the implicit solvation model SMD showed reliable performance. Hence, this combination was used for all quantum-chemical calculations performed in this work.⁴⁶

Methyl cation affinities (MCA)^47,48 often characterise the reactivity of nucleophiles (Nuc:) towards C-centred electrophiles⁴⁹ better than pK_aH values, which reflect the thermodynamics of ⁺Nuc–H bond formations. We, therefore, calculated MCAs for phosphines PR₃, as shown in Scheme 5, from the Gibbs reactions energies of methylation reactions in dichloromethane (MCA = −ΔG₂₉₈) (see Table 4 and ESI† for details).

Scheme 5 Reaction scheme for the calculation of PR₃ methyl cation affinities (MCA) in dichloromethane.

Table 4 Methyl cation affinities (MCA), experimentally determined reaction barriers (ΔG^‡_exp) as well as quantum-chemically calculated reaction barriers (ΔG^‡_calc) and reaction energies (ΔG_add) for the addition of phosphines PR₃ to the Michael acceptors 1, 2 and 3 in dichloromethane (all energies in kJ mol⁻¹)

PR3	MCA^a	Ethyl acrylate (1)			Ethyl allenoate (2)			Ethyl propiolate (3)
		ΔG^‡exp^b	ΔG^‡calc^c	ΔGadd^d	ΔG^‡exp^b	ΔG^‡calc^c	ΔGadd^d	ΔG^‡exp^b	ΔG^‡calc^c	ΔGadd^d
a MCA (= −ΔG298) calculated according to Scheme 5 at the SMD(DCM)/MN15/def2-TZVPP level of theory at 298.15 K. b Gibbs activation energies ΔG^‡exp calculated from the experimentally determined second-order rate constants k2 (20 °C) in Table 2 by using the Eyring equation. c Gibbs activation energies ΔG^‡calc of the reactions in Scheme 6 calculated at the SMD(DCM)/MN15/def2-TZVPP level of theory at 298.15 K. d Gibbs reaction energies ΔGadd of the reactions in Scheme 6 calculated at the SMD(DCM)/MN15/def2-TZVPP level of theory at 298.15 K.
P(pfp)3	402.8	97.9	90.8	73.0	85.6	88.6	7.7	86.0	89.8	29.3
PPh3	418.6	93.1	89.9	68.5	83.6	87.7	5.5	82.9	87.9	27.7
P(ani)3	425.7	88.8	86.2	61.1	79.8	87.5	−0.8	78.9	84.6	18.6
PMePh2	434.5	87.4	86.5	51.8	78.6	87.8	−10.8	78.5	86.7	18.1
PMe2Ph	448.6	81.3	80.6	33.9	75.0	83.7	−23.3	74.8	82.2	4.6
PBu3	459.7	78.7	79.2	32.2	72.9	83.6	−31.8	71.9	79.7	−3.6
PMe3	466.1	76.8	79.2	22.0	71.8	82.7	−33.6	71.9	80.2	−5.9
PCy3	473.0	79.7	81.5	34.7	76.9	81.9	−7.1	70.9	71.9	−7.2

---

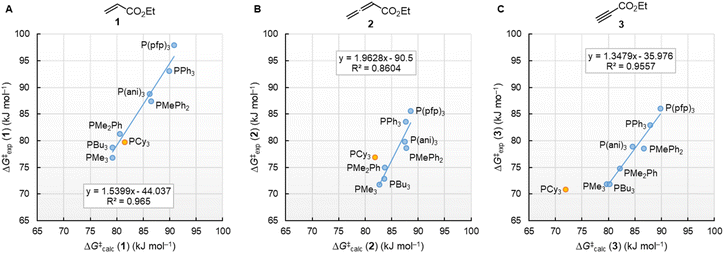
Fig. 10 illustrates that the experimentally determined Gibbs activation energies ΔG^‡_exp of PR₃ additions to Michael acceptors 1, 2, and 3 (20 °C, CH₂Cl₂), except for PCy₃, correlate linearly with the quantum-chemically calculated MCAs. Thus, we can conclude that the easily calculated thermodynamics of methylation reactions can be used to predict relative nucleophilicities of sterically unencumbered PR₃ also towards other classes of C-electrophiles, such as electron-deficient π-systems.

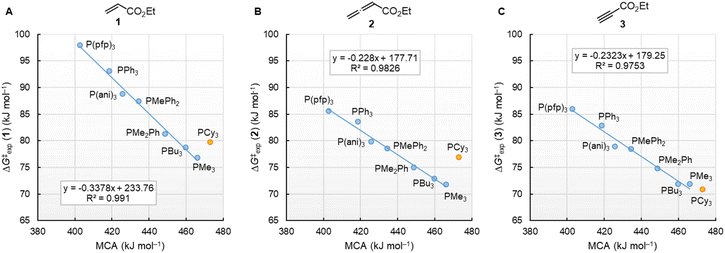Fig. 10 Correlation of experimental Gibbs activation energies ΔG^‡_exp with computed MCA values of PR₃ additions to (A) ethyl acrylate (1), (B) ethyl allenoate (2), and (C) ethyl propiolate (3) in dichloromethane. With energies from Table 4, data for the sterically encumbered PCy₃ excluded when constructing the correlation lines.

By using the same DFT level of theory as for the MCA calculations, we then analysed the energetics of PR₃ additions to Michael acceptors 1, 2, and 3 (Scheme 6) by calculating the reaction barriers ΔG^‡_calc and the Gibbs reaction energies for the addition step ΔG_add (Table 4).

Scheme 6 Gibbs activation (ΔG^‡_calc) and reaction energies (ΔG_add) of PR₃ additions to Michael acceptors 1–3.

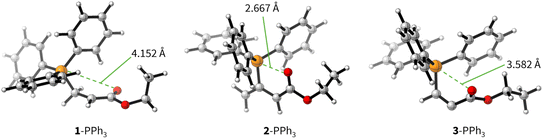
The positive ΔG_add values for PR₃ additions to 1 (Table 4) are in accord with the experimentally observed reversibility of these reactions. For 2 and particularly 3 only the most reactive and Lewis basic phosphines react exergonically. In general, PR₃ additions to the allenoate 2 are energetically more favourable than the corresponding reactions of phosphines with 1 or 3. We rationalise the differences in the stability of the zwitterionic PR₃-adducts derived from 1, 2, and 3 by the variable extent of attractive P⋯O interactions in the adducts.²⁵Fig. 11 depicts the optimised geometries of the adducts of 1, 2, or 3 with PPh₃, the most relevant phosphine in organocatalysis. The computed P–O distances in the PPh₃ adducts of 2, 3, and 1 follow the trend seen in ΔG_add: the shorter the P–O distance the more stable is the adduct.

Fig. 11 Molecular structures of the zwitterionic adducts of PPh₃ with 1, 2, and 3 optimised at SMD(DCM)/MN15/def2-TZVPP level of theory. Green dashed lines indicate relevant P–O distances in the adducts.

The correlation lines in Fig. 12 indicate that the activation barriers (ΔG^‡_exp) of phosphine additions to the vinylic, allenic, and acetylenic electrophiles decrease systematically as the thermodynamic driving forces (ΔG_add) increase. However, the slopes in Fig. 12A–C reflect that only 39%, 30%, and 37% of the product stabilising effects are found in the transition states (TS) of these phospha-Michael additions.

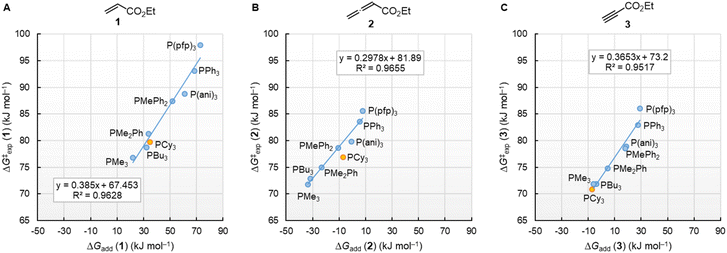Fig. 12 Correlations of ΔG^‡_exp (20 °C) for PR₃ additions to (A) 1, (B) 2, and (C) 3 in dichloromethane with the respective reaction energies ΔG_add. With energies from Table 4, data for the sterically encumbered PCy₃ excluded when constructing the correlation lines.

Neglecting the effect of the small temperature difference between experimental and calculated energies (20 °C vs. 25 °C), the quantum-chemically calculated reaction barriers (ΔG^‡_calc) for phosphine additions to 1, 2, and 3 are within a range of ±10 kJ mol⁻¹ of the experimentally determined Gibbs activation energies ΔG^‡_exp (Table 4). The excellent linear correlations of ΔG^‡_exp with ΔG^‡_calc in Fig. 13 corroborate the interpretation that the experimentally measured second-order rate constants k₂ reflect the initial phosphine addition to the electron-deficient reaction partners. We note, however, that the regression lines for all three Michael acceptors show slopes significantly larger than unity, which implies that the 20 kJ mol⁻¹ wide range for ΔG^‡_exp is compressed to a width of only 10 kJ mol⁻¹ in the DFT calculations.

Fig. 13 Correlation of experimentally determined ΔG^‡_exp (20 °C) for PR₃ additions to (A) 1, (B) 2, and (C) 3 in dichloromethane with quantum-chemically calculated Gibbs activation energies (ΔG^‡_calc). Results for PCy₃ were excluded when calculating the regression lines.

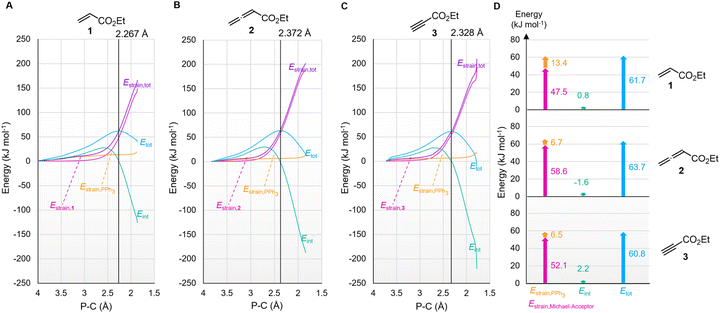
Transition state (TS) geometries for the addition of PPh₃ to Michael acceptors 1, 2, and 3 are shown in Fig. 14. In contrast to the PPh₃ adduct with 2, where the attractive P⋯O interaction was identified as a key stabilising factor, the P⋯O distance in the TS geometries of PPh₃ reactions with 1, 2, and 3 are generally >3.5 Å and exceed the sum of the van der Waals radii of oxygen and phosphorus (3.22 Å, with O: 1.52 Å and P: 1.80 Å).⁵⁰ The P–C bond formation is slightly more advanced in TS-1-PPh₃ (P–C distance: 2.267 Å) than in TS-2-PPh₃ (2.372 Å) or TS-3-PPh₃ (2.328 Å), which indicates a later TS for the addition of PPh₃ to 1 than for the analogous reaction with 2 and 3. Likewise, charge separation (NBO analysis) between PPh₃ and the respective electrophile in the TS is found to be already larger for acrylate 1 than for 2 or 3: the cumulative partial charges in TS-1-PPh₃ are ±0.492 and amount to only ±0.396 in TS-2-PPh₃ and TS-3-PPh₃, respectively. The origin of the variations in the reaction barrier (ΔG^‡) were subsequently investigated by using the Marcus eqn (1) to calculate intrinsic barriers (ΔG^‡₀).⁴³

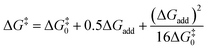Fig. 14 TS geometries for the addition of PPh₃ to 1 (TS-1-PPh₃), 2 (TS-2-PPh₃), and 3 (TS-3-PPh₃) with selected P–O (green dashed line) and P–C (black dashed line) distances as well as charge separation (based on cumulated NBO charges on the fragments) of PPh₃ and the corresponding Michael acceptor (level of theory: SMD(DCM)/MN15/def2-TZVPP).

The intrinsic barriers ΔG^‡₀ (Table 5) obtained by combining experimental or theoretically calculated reaction barriers with the DFT-calculated ΔG_add show identical trends. The ΔG^‡₀ for reactions with the Michael acceptor 1, which changes hybridisation from sp² to sp³ at the reaction centre, are significantly lower than those for analogous PR₃ additions to 2 and 3, which involve the need for a higher degree of reorganisation owing to the change from sp- to sp²-hybridisation at the electrophilic centre (see Table 5). Nevertheless, the more favourable reaction energies ΔG_add for PR₃ additions to 2 and 3 give rise to the overall lower reaction barriers (ΔG^‡) and thus faster reaction rates, despite higher intrinsic barriers than for PR₃ additions to the acrylate 1.

Table 5 Computed intrinsic barriers for addition of phosphines to 1, 2 and 3 according to eqn (1). ΔG^‡_0,calc refers to intrinsic barriers calculated with computed reaction barriers (SMD(DCM)/MN15/def2-TZVPP data). ΔG^‡_0,exp refers to the use of experimentally determined reaction barriers in eqn (1)

PR3	Ethyl acrylate (1)		Ethyl allenoate (2)		Ethyl propiolate (3)
	ΔG^‡0,exp	ΔG^‡0,calc	ΔG^‡0,exp	ΔG^‡0,calc	ΔG^‡0,exp	ΔG^‡0,calc
P(pfp)3	55.4	47.3	81.7	84.7	70.6	74.4
PPh3	53.4	49.8	80.8	84.9	68.3	73.4
P(ani)3	53.9	51.1	80.2	87.9	69.3	75.0
PMePh2	58.6	57.7	83.9	93.1	69.2	77.4
PMe2Ph	63.2	62.5	86.3	95.0	72.5	79.9
PBu3	61.6	62.1	88.1	98.9	73.7	81.5
PMe3	65.3	67.8	87.8	98.8	74.8	83.1
PCy3	61.1	63.0	80.4	85.4	74.5	75.5

---

The origin of the characteristic differences in the intrinsic barriers in the reaction series for 1 (ΔG^‡_0,exp = 53 to 65 kJ mol⁻¹), 2 (80 to 88 kJ mol⁻¹), and 3 (68 to 75 kJ mol⁻¹) were further scrutinised by analysing deformation energies according to the activation strain model.⁵¹ The P–C distance (highlighted in the TS geometries in Fig. 14) was used as the reaction coordinate to analyse the activation strain energetics for the addition of PPh₃ to Michael acceptors 1, 2, and 3 (Fig. 15). The calculated overall deformation energies (E_strain,tot) are dominated by the deformation energies (E_strain) of the electrophiles 1–3, while the deformation energies of PPh₃ are comparatively small. The deformation energy for Michael acceptor 1 (47.5 kJ mol⁻¹) is significantly smaller than E_strain for Michael acceptors 2 (58.6 kJ mol⁻¹) or 3 (52.1 kJ mol⁻¹), in accord with the ordering of the Marcus intrinsic barriers in Table 5 (53.4 kJ mol⁻¹ for 1 + PPh₃, 68.3 kJ mol⁻¹ for 3 + PPh₃, and 80.8 kJ mol⁻¹ for 2 + PPh₃). For all reactions in Fig. 15, the interaction energies (E_int) are destabilising at early stages of the P⋯C bond-formation and only become stabilising when approaching the TS region.

Fig. 15 Activation strain analyses for the addition of PPh₃ to 1 (A), 2 (B) and 3 (C). Deformation energies of the Michael acceptor (magenta) and PPh₃ (orange) and the total deformation (purple) as well as interaction energies (green) and relative energy of a molecular complex along the reaction coordinate (blue) are depicted. The TS is highlighted by the vertical grey line. (D) Distortion–interaction analysis of the TS corresponding to (A)–(C) (level of theory: SMD(DCM)/MN15/def2-TZVPP).

Conclusion

Phosphine additions to electron-deficient π-systems play a key role in many Lewis-base catalysed organic reactions. In this work, we determined second-order rate constants k₂ for the additions of differently substituted tertiary phosphines PR₃ to ethyl acrylate, ethyl allenoate, and ethyl propiolate in dichloromethane at 20 °C. The reactivities of PR₃ quantified in this way correlate linearly with a range of PR₃ properties, for example their S_N2 and S_N1 reactivities towards other types of electrophilic reaction partners or their Brønsted and Lewis basicities. In addition, the experimentally determined Gibbs activation energies correlate with theoretically calculated barriers for the phospha-Michael additions as well as with theoretically calculated reaction energies in dichloromethane (SMD solvent model) suggesting the potential to anchor future quantum-chemical modeling of PR₃ reactions to experiments.

Gibbs energy profiles for the phospha-Michael addition reactions can be constructed from the experimental Gibbs activation energies (ΔG^‡) and the DFT-calculated Gibbs reaction energies (ΔG_add). Fig. 16 shows the energy profiles for reactions of 1, 2, or 3 with PPh₃, which is the most frequently used phosphine catalyst in organocatalytic transformations. The energy profiles for PPh₃ additions to acrylate 1 and allenoate 2 (or propiolate 3) immediately reveal that the addition barriers are surprisingly similar, while the reaction energies are largely different (Fig. 16). The by 27.4 kJ mol⁻¹ higher intrinsic barrier ΔG^‡_0,exp for the PPh₃ addition to 2 than to 1 (cf.Table 5) largely compensates the effect of the higher thermodynamic driving force for the adduct formation with 2 (0.5ΔΔG_add = 31.5 kJ mol⁻¹). As a consequence, the energetic barrier for the retroaddition of the endergonic 1+PPh₃ reaction is only 24.6 kJ mol⁻¹. In contrast, the analogous dissociation of the 2 + PPh₃-adduct proceeds over an energetic barrier of 78.1 kJ mol⁻¹.

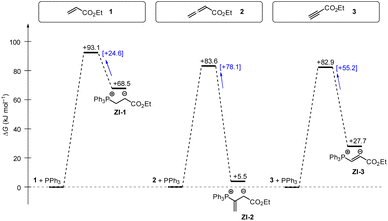Fig. 16 Gibbs energy profiles for PPh₃ additions to Michael acceptors 1, 2 and 3 in dichloromethane solution. Experimentally determined Gibbs activation energies ΔG^‡_exp are combined with quantum-chemically calculated reaction energies ΔG_add (data from Table 4). Reaction barriers for the retro-additions [ΔG^‡_retro] are given in square brackets.

In the context of multicomponent reactions, such as the Lu reaction (Fig. 17), which starts with a phosphine catalyst in a mixture of competing electrophiles, higher effective concentrations of zwitterionic PR₃-allenoate adducts than for the analogous PR₃-acrylate adducts may be one of the origins for the chemoselectivity of this cycloaddition.

Fig. 17 PR₃-catalysed Lu cycloaddition (Acc = electron-accepting group, E = ester group).

Tributylphosphine PBu₃ is more nucleophilic and Lewis basic than PPh₃. At first glance and neglecting the practical challenges associated with handling air-sensitive catalysts, PBu₃ might therefore appear to be a generally more effective Lewis base catalyst than PPh₃. The reaction profile of PBu₃ addition to allenoate 2 in Fig. 18 reveals, however, that the favourable thermodynamics for the zwitterionic adduct formations is linked to a rather large barrier for the heterolytic P–C bond cleavage. In phosphine catalysis this may imply that the final step of the catalytic cycle (e.g. in Fig. 17), that is the release of the PR₃ catalyst, may become unfavourably slow. As a consequence, optimisation of reaction conditions regularly requires to keep a delicate balance between formation of a sufficient concentration of PR₃ adducts by using highly reactive (nucleophilic) and Lewis basic phosphines and the antagonistic necessity of installing good PR₃ nucleofuges that allow for the efficient release of the catalyst in the final step of the catalytic cycle. The combination of experimental and quantum-chemical data to characterise the philicity/fugality features of tertiary phosphines in this work may therefore be helpful to guide future attempts to use phosphine catalysis in organic synthesis.

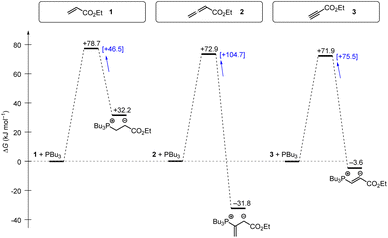Fig. 18 Gibbs energy profiles for PBu₃ additions to Michael acceptors 1, 2 and 3 in dichloromethane solution. Experimentally determined Gibbs activation energies ΔG^‡_exp are combined with quantum-chemically calculated reaction energies ΔG_add (data from Table 4). Reaction barriers for the retro-additions [ΔG^‡_retro] are given in square brackets.

Not all steps of phosphine-catalysed reactions are well accessible by experiment, e.g. in the Lu reaction. Further quantum-chemical investigations of the full cycle of phosphine-catalysed reactions are, therefore, ongoing to gain further insight in the relevant factors that need to be understood for a systematic improvement of these versatile reactions.

Data availability

The data supporting this article have been included as part of the ESI.†

Author contributions

Project conceptualisation and funding acquisition were done jointly by Y. W., M. S., H. Z. and A. R. O. Experimental methodology development and kinetic investigations were carried out by F. A. and supervised by A. R. O. Results of the kinetic measurements were formally analysed and visualised by F. A. and A. R. O. Quantum-chemical investigations, supervised by H. Z., were performed, analysed and visualised by H. J. and J. B. Results were discussed with Y. W. and M. S. The manuscript was written jointly by H. Z., J. B. and A. R. O. with input from all authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was funded by the Deutsche Forschungsgemeinschaft DFG (project number 410831260) and the National Natural Science Foundation of China (NSFC, project number 21861132014). Jan Brossette is funded by Deutsche Forschungsgemeinschaft (RTG 2620 Ion Pair Effects in Molecular Reactivity, project number 426795949). We gratefully acknowledge generous support for this project through the Leibniz-Rechenzentrum (LRZ) in Munich.

References

1. (a) L. Horner and K. Klüpfel, Zum Nachweis des polaren Charakters in Doppelbindungs-Systemen Phosphororganische Verbindungen II, Liebigs Ann. Chem., 1955, 591, 69–98; (b) L. Horner, W. Jurgeleit and K. Klüpfel, Zur anionotropen Polymerisationsauslösung bei Olefinen Tertiäre Phosphine III, Liebigs Ann. Chem., 1955, 591, 108–117.
2. K.-i. Morita, Z. Suzuki and H. Hirose, A Tertiary Phosphine-catalyzed Reaction of Acrylic Compounds with Aldehydes, Bull. Chem. Soc. Jpn., 1968, 41, 2815.
3. D. Basavaiah, B. S. Reddy and S. S. Badsara, Recent Contributions from the Baylis-Hillman Reaction to Organic Chemistry, Chem. Rev., 2010, 110, 5447–5674.
4. Y. Wei and M. Shi, Recent Advances in Organocatalytic Asymmetric Morita–Baylis–Hillman/aza-Morita–Baylis–Hillman Reactions, Chem. Rev., 2013, 113, 6659–6690.
5. Reviews: (a) X. Lu, C. Zhang and Z. Xu, Reactions of Electron-Deficient Alkynes and Allenes under Phosphine Catalysis, Acc. Chem. Res., 2001, 34, 535–544; (b) L.-W. Ye, J. Zhou and Y. Tang, Phosphine-triggered synthesis of functionalized cyclic compounds, Chem. Soc. Rev., 2008, 37, 1140–1152; (c) Z. Wang, X. Xu and O. Kwon, Phosphine catalysis of allenes with electrophiles, Chem. Soc. Rev., 2014, 43, 2927–2940; (d) M. Shi, Y. Wei, M.-X. Zhao and J. Zhang, Organocatalytic Cycloadditions for Synthesis of Carbo- and Heterocycles, Wiley-VCH, Weinheim, 2018; (e) Y. Huang, J. Liao, W. Wang, H. Liu and H. Guo, Synthesis of heterocyclic compounds through nucleophilic phosphine catalysis, Chem. Commun., 2020, 56, 15235–15281; (f) Y. Wei and M. Shi, Asymmetric Reactions Catalyzed by Chiral Tertiary Phosphines, Chin. J. Chem., 2020, 38, 1395–1421; (g) C. Xie, A. J. Smaligo, X.-R. Song and O. Kwon, Phosphorus-Based Catalysis, ACS Cent. Sci., 2021, 7, 536–558.
6. (a) A. V. Salin, A. V. Il’in, F. G. Shamsutdinova, A. R. Fatkhutdinov, D. R. Islamov, O. N. Kataeva and V. I. Galkin, The Pudovik Reaction Catalyzed by Tertiary Phosphines, Curr. Org. Synth., 2013, 13, 132–141; (b) J. T. Maddigan-Wyatt, M. T. Blyth, J. Ametovski, M. L. Coote, J. F. Hooper and D. W. Lupton, Redox Isomerization/(3+2) Allenoate Annulation by Auto-Tandem Phosphine Catalysis, Chem. - Eur. J., 2021, 27, 16232–16236.
7. (a) C. Gimbert, M. Lumbierres, C. Marchi, M. Moreno-Mañas, R. M. Sebastián and A. Vallribera, Michael additions catalyzed by phosphines. An overlooked synthetic method, Tetrahedron, 2005, 61, 8598–8605; (b) D. Enders, A. Saint-Dizier, M.-I. Lannou and A. Lenzen, The Phospha-Michael Addition in Organic Synthesis, Eur. J. Org Chem., 2006, 29–49.
8. (a) S. E. Denmark and G. L. Beutner, Lewis Base Catalysis in Organic Synthesis, Angew. Chem., Int. Ed., 2008, 47, 1560–1638; (b) S. Lakhdar, Quantitative Treatments of Nucleophilicity and Carbon Lewis Basicity, in Lewis Base Catalysis in Organic Synthesis, ed. E. Vedejs and S. E. Denmark, Wiley-VCH, Weinheim, 1st edn, 2016, pp. 85–118; (c) H. Guo, Y. C. Fan, Z. Sun, Y. Wu and O. Kwon, Phosphine Organocatalysis, Chem. Rev., 2018, 118, 10049–10293; (d) S. B. Nallapati and S.-C. Chuang, Phosphine-Catalyzed Reactions with Unsaturated Carbonyl Compounds, Asian J. Org. Chem., 2018, 7, 1743–1757; (e) S. Khong, T. Venkatesh and O. Kwon, Nucleophilic Phosphine Catalysis: The Untold Story, Asian J. Org. Chem., 2021, 10, 2699–2708; (f) Y. Meng, L. Chen and E.-Q. Li, Recent Advances in Lewis Base-Catalysed Chemo-, Diastereo- and Enantiodivergent Reactions of Electrondeficient Olefins and Alkynes, Chem. Rec., 2022, 22, e202100276; (g) A. V. Salin and S. A. Shabanov, Advances in organocatalysis of the Michael reaction by tertiary phosphines, Catal. Rev., 2023, 1–90; (h) Q.-F. Li, J. Ma, J. Meng and E.-Q. Li, Recent Advances in Nucleophilic Lewis Base-Catalyzed Cycloadditions for Synthesis of Spirooxindoles, Adv. Synth. Catal., 2023, 365, 4412–4439.
9. H. Ni, W.-L. Chan and Y. Lu, Phosphine-Catalyzed Asymmetric Organic Reactions, Chem. Rev., 2018, 118, 9344–9411.
10. T. K. Heiss, R. S. Dorn and J. A. Prescher, Bioorthogonal Reactions of Triarylphosphines and Related Analogues, Chem. Rev., 2021, 121, 6802–6849.
11. A. V. Salin, A. R. Fatkhutdinov, A. V. Il’in, E. I. Sotov, A. A. Sobanov, V. I. Galkin and B. R. James, Mechanistic aspects of reactions of triphenylphosphine with electron-deficient alkenes in acetic acid solution, J. Phys. Org. Chem., 2013, 26, 675–678.
12. A. V. Salin, A. R. Fatkhutdinov, A. V. Il’in, V. I. Galkin and F. G. Shamsutdinova, Solvent Effect on Kinetics and Mechanism of the Phospha-Michael Reaction of Tertiary Phosphines with Unsaturated Carboxylic Acids, Heteroat. Chem., 2014, 25, 205–216.
13. A. V. Salin, Mechanistic insights into phospha-Michael reaction of tertiary phosphines with electron-deficient alkenes, Phosphorus, Sulfur Silicon Relat. Elem., 2016, 191, 1625–1627.
14. A. V. Salin, A. A. Shabanov, K. R. Khayarov, R. I. Nugmanov and D. R. Islamov, Stereoelectronic Effect in the Reaction of α-Methylene Lactones with Tertiary Phosphines and Its Applications in Organocatalysis, J. Org. Chem., 2023, 88, 11954–11967.
15. F. An, H. Jangra, Y. Wei, M. Shi, H. Zipse and A. R. Ofial, Reactivities of allenic and olefinic Michael acceptors towards phosphines, Chem. Commun., 2022, 58, 3358–3361.
16. A reactivity ratio of k(1)/k(2) = 111 was reported for the Michael addition of pyrrolidine (in CHCl₃): C. Kiattisewee, A. Kaidad, C. Jiarpinitnun and T. Luanphaisarnnont, Kinetic studies of conjugate addition of amines to allenic and acrylic esters and their correlation with antibacterial activities against Staphylococcus aureus, Monatsh. Chem., 2018, 149, 1059–1068.
17. H. Hoffmann, Zur Reaktion von Triphenylphosphin mit Olefinen, Chem. Ber., 1961, 94, 1331–1336.
18. The alkylation of PPh₃ by methyl acrylate in the presence of triflic acid was described in: B. Patzke and R. Sustmann, Dimerization of methyl acrylate by homogeneous transition metal catalysis. Part II. Activation of dihydridoruthenium(II)phosphane complexes by CF₃SO₃H, J. Organomet. Chem., 1994, 480, 65–74.
19. H. Ohmori, T. Takanami, H. Shimada and M. Masui, Simple Preparation of 3-Oxoalkyltriphenylphosphonium Salts Effected by Using 2,6-Lutidinium Salts, Chem. Pharm. Bull., 1987, 35, 2558–2560.
20. S. Tshepelevitsh, A. Kütt, M. Lõkov, I. Kaljurand, J. Saame, A. Heering, P. G. Plieger, R. Vianello and I. Leito, On the Basicity of Organic Bases in Different Media, Eur. J. Org Chem., 2019, 2019, 6735–6748.
21. M. S. Robinson, M. L. Polak, V. M. Bierbaum, C. H. DePuy and W. C. Lineberger, Experimental Studies of Allene, Methylacetylene, and the Propargyl Radical: Bond Dissociation Energies, Gas-Phase Acidities, and Ion–Molecule Chemistry, J. Am. Chem. Soc., 1995, 117, 6766–6778.
22. Y. Ben-Tal, P. J. Boaler, H. J. A. Dale, R. E. Dooley, N. A. Fohn, Y. Gao, A. García-Domínguez, K. M. Grant, A. M. R. Hall, H. L. D. Hayes, M. M. Kucharski, R. Wei and G. C. Lloyd-Jones, Mechanistic analysis by NMR spectroscopy: A users guide, Prog. Nucl. Magn. Reson., 2022, 129, 28–106.
23. T. Lemek and H. Mayr, Electrophilicity Parameters for Benzylidenemalononitriles, J. Org. Chem., 2003, 68, 6880–6886.
24. X. Lu, Z. Lu and X. Zhang, Phosphine-catalyzed one-pot synthesis of cyclopentenes from electron-deficient allene, malononitrile and aromatic aldehydes, Tetrahedron, 2006, 62, 457–460.
25. Y. Liang, S. Liu, Y. Xia, Y. Li and Z.-X. Yu, Mechanism, Regioselectivity, and the Kinetics of Phosphine-Catalyzed [3+2] Cycloaddition Reactions of Allenoates and Electron-Deficient Alkenes, Chem. - Eur. J., 2008, 14, 4361–4373.
26. Q. Chen, P. Mayer and H. Mayr, Ethenesulfonyl Fluoride: The Most Perfect Michael Acceptor Ever Found?, Angew. Chem., Int. Ed., 2016, 55, 12664–12667.
27. Reactivities of further, sterically demanding PR₃ were studied in: E. Follet, P. Mayer, D. S. Stephenson, A. R. Ofial and G. Berionni, Reactivity-Tuning in Frustrated Lewis Pairs: Nucleophilicity and Lewis Basicity of Sterically Hindered Phosphines, Chem. - Eur. J., 2017, 23, 7422–7427.
28. (a) F. G. Bordwell, J. C. Branca and T. A. Cripe, Brønsted β_Nu Values and Leaving Group Effects in S_N2 Reactions. Tests of the Reactivity—Selectivity Postulate, Isr. J. Chem., 1985, 26, 357–366; (b) H. Mayr and A. R. Ofial, The Reactivity-Selectivity Principle: An Imperishable Myth in Organic Chemistry, Angew. Chem., Int. Ed., 2006, 45, 1844–1854.
29. (a) W. A. Henderson Jr and C. A. Streuli, The Basicity of Phosphines, J. Am. Chem. Soc., 1960, 82, 5791–5794; (b) W. A. Henderson Jr and S. A. Buckler, The Nucleophilicity of Phosphines, J. Am. Chem. Soc., 1960, 82, 5794–5800.
30. (a) T. Allman and R. G. Goel, The basicity of phosphines, Can. J. Chem., 1982, 60, 716–722; (b) P. M. Zizelman, C. Amatore and J. K. Kochi, Steric and Electronic Effects in Ligand Substitution of Metal Carbonyls. Rapid Kinetics of Labile Carbonylmanganese Complexes by Transient Electrochemical Techniques, J. Am. Chem. Soc., 1984, 106, 3771–3784.
31. L. A. P. Kane-Maguire, E. D. Honig and D. A. Sweigart, Nucleophilic addition to coordinated cyclic π-hydrocarbons: mechanistic and synthetic studies, Chem. Rev., 1984, 84, 525–543.
32. N. P. Taylor, J. A. Gonzalez, G. S. Nichol, A. García-Domínguez, A. G. Leach and G. C. Lloyd-Jones, A Lewis Base Nucleofugality Parameter, N^F_B, and its Application in an Analysis of MIDA-boronate Hydrolysis Kinetics, J. Org. Chem., 2022, 87, 721–729.
33. T. Kanzian, T. A. Nigst, A. Maier, S. Pichl and H. Mayr, Nucleophilic Reactivities of Primary and Secondary Amines in Acetontrile, Eur. J. Org Chem., 2009, 6379–6385.
34. J. Ammer, M. Baidya, S. Kobayashi and H. Mayr, Nucleophilic reactivities of tertiary alkylamines, J. Phys. Org. Chem., 2010, 23, 1029–1035.
35. J. P. Richard, M. M. Toteva and J. Crugeiras, Structure−Reactivity Relationships and Intrinsic Reaction Barriers for Nucleophile Additions to a Quinone Methide: A Strongly Resonance-Stabilized Carbocation, J. Am. Chem. Soc., 2000, 122, 1664–1674.
36. T. B. Phan, M. Breugst and H. Mayr, Towards a General Scale of Nucleophilicity?, Angew. Chem., Int. Ed., 2006, 45, 3869–3874.
37. R. J. Mayer, T. Tokuyasu, P. Mayer, J. Gomar, S. Sabelle, B. Mennucci, H. Mayr and A. R. Ofial, Solvation Accounts for the Counter-Intuitive Nucleophilicity Ordering of Peroxide Anions, Angew. Chem., Int. Ed., 2017, 56, 13279–13282.
38. J. G. Atton and L. A. P. Kane-Maguire, Kinetics of nucleophilic attack on co-ordinated organic moieties. Part 21. Factors governing the nucleophilicity of phosphorus nucleophiles towards [Fe(CO)₃(1–5-η-C₆H₇)]⁺, J. Chem. Soc., Dalton Trans., 1982, 1491–1498.
39. H. Mayr and A. R. Ofial, Philicity, fugality, and equilibrium constants: when do rate-equilibrium relationships break down?, Pure Appl. Chem., 2017, 89, 729–744 ; and refs cited therein..
40. M. Baidya, S. Kobayashi, F. Brotzel, U. Schmidhammer, E. Riedle and H. Mayr, DABCO or DMAP – Why Are They Different in Organocatalysis?, Angew. Chem., Int. Ed., 2007, 46, 6476–6479.
41. H. Mayr, S. Lakhdar, B. Maji and A. R. Ofial, A quantitative approach to nucleophilic organocatalysis, Beilstein J. Org. Chem., 2012, 8, 1458–1478.
42. B. Maji, X.-H. Duan, P. M. Jüstel, P. A. Byrne, A. R. Ofial and H. Mayr, Nucleophilicities and Nucleofugalities of Thio- and Selenoethers, Chem. - Eur. J., 2021, 27, 11367–11376.
43. (a) R. A. Marcus, Theoretical relations among rate constants, barriers, and Broensted slopes of chemical reactions, J. Phys. Chem., 1968, 72, 891–899; (b) R. A. Marcus, Unusual slopes of free energy plots in kinetics, J. Am. Chem. Soc., 1969, 91, 7224–7225; (c) W. J. Albery, The Application of the Marcus Relation to Reactions in Solution, Annu. Rev. Phys. Chem., 1980, 31, 227–263.
44. B. Maji, M. Baidya, J. Ammer, S. Kobayashi, P. Mayer, A. R. Ofial and H. Mayr, Nucleophilic Reactivities and Lewis Basicities of 2-Imidazolines and Related N-Heterocyclic Compounds, Eur. J. Org Chem., 2013, 3369–3377.
45. (a) Y. Xia, Y. Liang, Y. Chen, M. Wang, L. Jiao, F. Huang, S. Liu, Y. Li and Z. X. Yu, An Unexpected Role of a Trace Amount of Water in Catalyzing Proton Transfer in Phosphine-Catalyzed (3+2) Cycloaddition of Allenoates and Alkenes, J. Am. Chem. Soc., 2007, 129, 3470–3471; (b) E. Mercier, B. Fonovic, C. Henry, O. Kwon and T. Dudding, Phophine triggered [3+2] allenoate-acrylate annulation: a mechanistic enlightenment, Tetrahedron Lett., 2007, 48, 3617–3620.
46. (a) H. S. Yu, X. He, S. L. Li and D. G. Truhlar, MN15: A Kohn–Sham global-hybrid exchange–correlation density functional with broad accuracy for multi-reference and single-reference systems and noncovalent interactions, Chem. Sci., 2016, 7, 5032–5051 ( Chem. Sci. , 2016 , 7 , 6278–6279 ); (b) F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305; (c) A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions, J. Phys. Chem. B, 2009, 113, 6378–6396.
47. D. Kadish, A. D. Mood, M. Tavakoli, E. S. Gutman, P. Baldi and D. L. Van Vranken, Methyl Cation Affinities of Canonical Organic Functional Groups, J. Org. Chem., 2021, 86, 3721–3729.
48. For MCAs of PR₃ in the gas phase, see: C. Lindner, R. Tandon, B. Maryasin, E. Larionov and H. Zipse, Phosphine-Catalyzed Asymmetric Organic Reactions, Beilstein J. Org. Chem., 2012, 8, 1406–1442.
49. J. Hine and R. D. Weimar Jr, Carbon Basicity, J. Am. Chem. Soc., 1965, 87, 3387–3396.
50. A. Bondi, van der Waals Volumes and Radii, J. Phys. Chem., 1964, 68, 441–451.
51. (a) F. M. Bickelhaupt and K. N. Houk, Analyzing Reaction Rates with the Distortion/Interaction-Activation Strain Model, Angew. Chem., Int. Ed., 2017, 56, 10070–10086; (b) P. Vermeeren, S. C. C. van der Lubbe, C. Fonseca Guerra, F. M. Bickelhaupt and T. A. Hamlin, Understanding chemical reactivity using the activation strain model, Nat. Protoc., 2020, 15, 649–667; (c) P. Vermeeren, T. A. Hamlin and F. M. Bickelhaupt, Chemical reactivity from an activation strain perspective, Chem. Commun., 2021, 57, 5880–5896.

---

Footnotes

† Electronic supplementary information (ESI) available: Additional figures, details of synthetic procedures, analytics and product characterisation, kinetic measurements, quantum-chemical calculations and geometries of optimised structures. See DOI: https://doi.org/10.1039/d4sc04852k

‡ These authors contributed equally to this work.

---